C语言第入门——第十六课
目录
一、分治策略与递归
二、递归
1.求解n的阶乘
2.输入整数、倒序输出
3.输入整数、正序输出
4.计算第n位Fibonacci数列
编辑5.无序整数数组打印
6.找到对应数组下标
一、分治策略与递归
在我们遇到大问题的时候,我们的正确做法是将它分解成小问题,然后一个小问题一个小问题解决,这样的策略就是分治策略。
递归是分治策略的一种方式,可以不断地通过自己调用自己来将问题规模逐渐缩小,从而解决问题。
分治策略的特征:
①大规模问题化成小规模问题容易被解决掉
②大规模问题能够被划分为多个相同的小规模问题
③这些小规模问题的解组合起来是大问题的解
④小规模问题是相互独立的
举个例子:
皇帝让你数10个谷仓的米粒,问题规模太大,你可以找100个工人,每人分上相同重量的米进行数,每个人的数量相加就是最终米粒的数量。
这就是一个典型的分治策略问题,将大规模转化为小规模问题,而且是满足上面分治策略的四条特征的。
分治策略不光在我们算法中需要使用,我希望转化成我们的思维模式,帮助我们更好的解决生活中的问题。
二、递归
递归包含两个过程:递推和回归,递推逐层调用,直到递推终止条件满足,再逐层回归。
递归和普通函数调用类似,需要开辟栈帧空间,它只有满足中止条件逐层回归的时候,上一层的函数的栈帧空间才会被释放。注意,不存在无限递归的函数,因为栈帧空间是有限的,所以不能无限调用函数,开辟空间。
递归分为直接递归和间接递归。
直接递归:在函数执行的时候调用函数自身。
间接递归:在函数执行过程中调用其他函数,再调用函数自身。
一般不推荐使用间接递归,因为很容易递推错误。
1.求解n的阶乘
代码如下:
int fabi(int n)
{if (n == 1) return 1;int sum = fabi(n-1)*n;return sum;
}int main()
{int n = 0;scanf("%d", &n);int sum =fabi(n);printf("%d", sum);
}
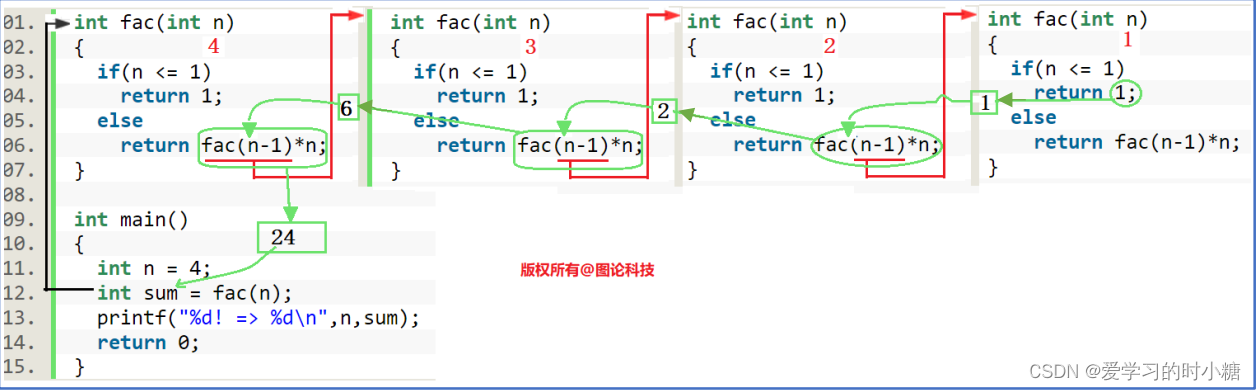
分析:我们将代码复制多份便于观看,但其实只有一个代码哦。
我们这里取n=4,第一次进入到fabi()函数中,n!=1,执行下一条语句fabi(n-1)*n,也就是fabi(3)*4。
然后我们再次调用函数fabi(),此时n=3,我们进入到函数体中n!=1,执行下一条语句fabi(2)*3。
此时我们再次调用fabi()函数,此时n=2,n!=1,执行fabi(1)*2。
这里再次调用fabi()函数,此时n==1,所以我们return 1。
返回到上一层,我们继续执行,此时这条语句为sum = 1*2,我们返回1*2,然后我们继续回归上一层函数,sum = 3*2*1,然后我们再回归,最后得到sum =4*3*2*1,回归结束。
下面第一张是我画的示意图,如果看不清楚再看下面第二张老师画的图,老师画的比较清晰。

红色的线代表递推过程,绿色的线代表回归过程。
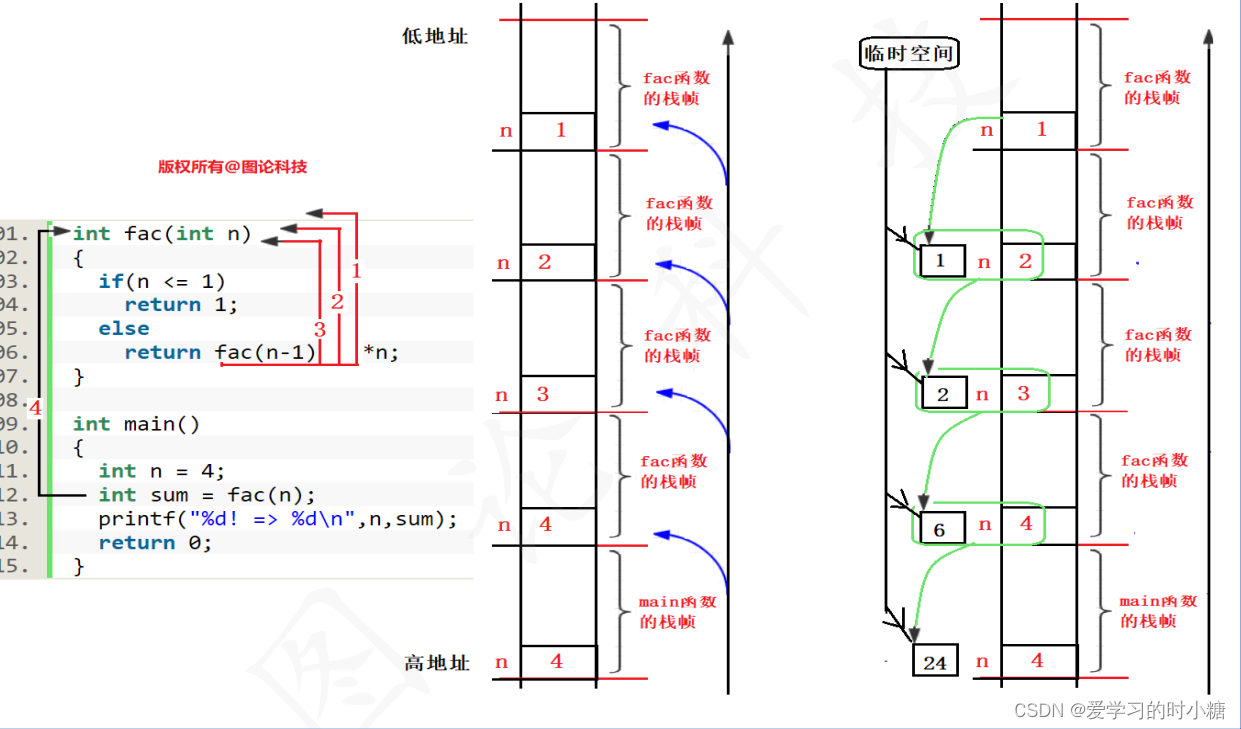
下面解释一下栈帧的动态变化情况。
在每次递推调用函数的时候,程序开辟栈帧空间,在回归的时候再一层层释放掉。
2.输入整数、倒序输出
输入一个整数(无符号整型),使用递归算法将整数倒序输出。
void Show(unsigned int n)
{if (n == 0) return ;else{printf("%d", n % 10);Show(n / 10);}
}
int main()
{unsigned int n = 0;scanf("%d", &n);Show(n);
}
逻辑图如下,变量和函数定义不太一样,但是逻辑一致。
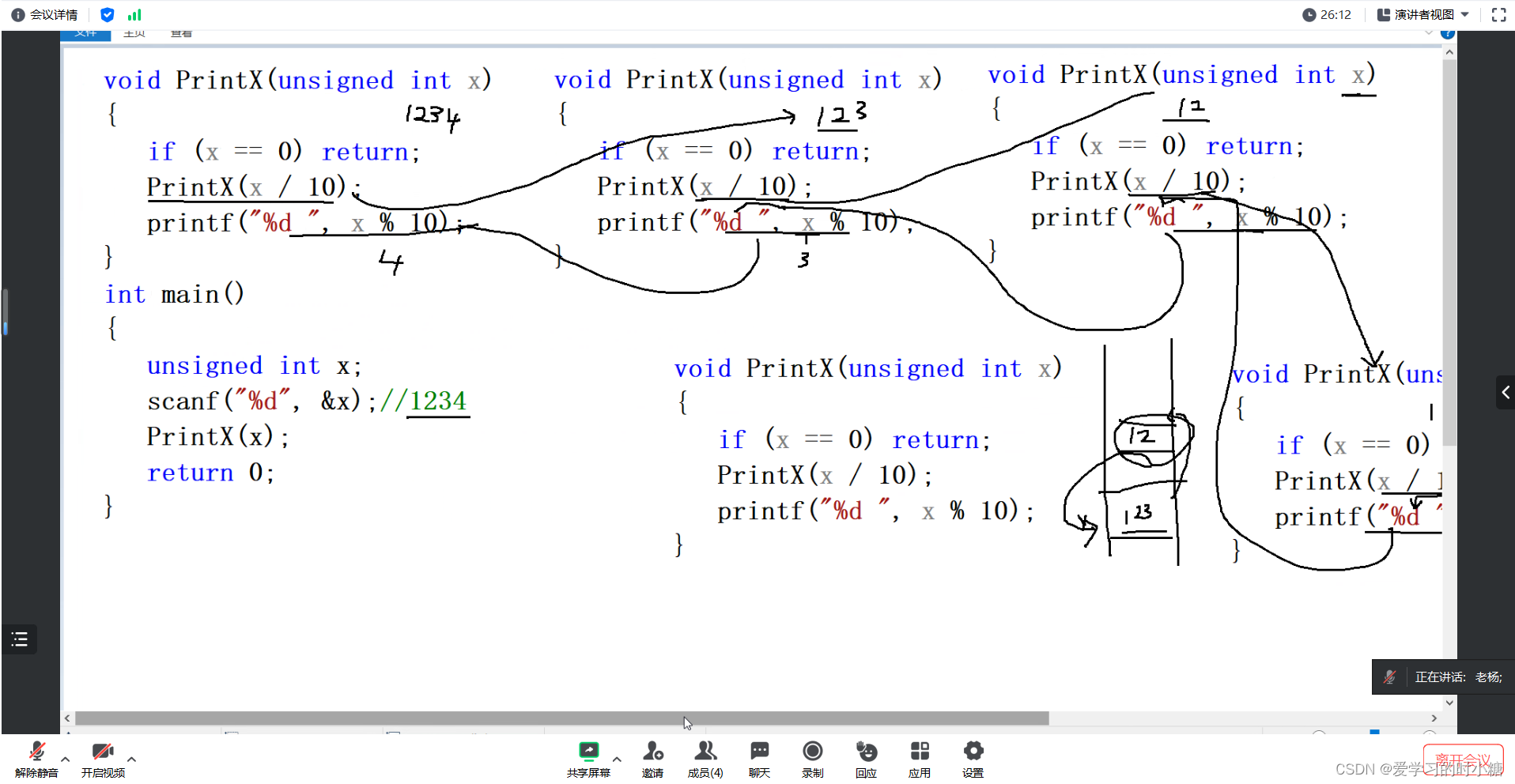
3.输入整数、正序输出
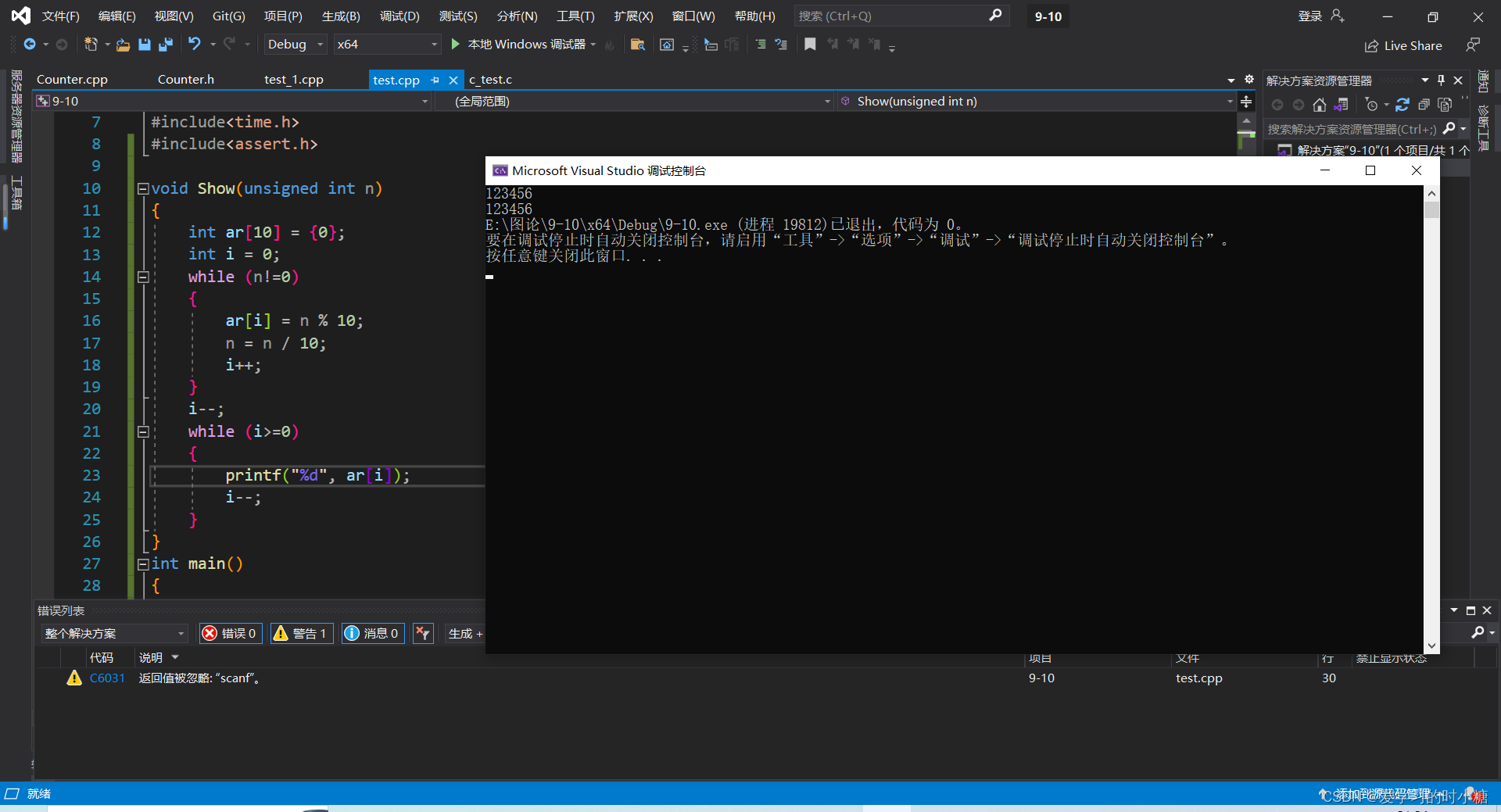
法一:数组法
void Show(unsigned int n)
{ int ar[10] = {0};int i = 0;while (n!=0){ar[i] = n % 10;n = n / 10;i++;}i--;while (i>=0){printf("%d ", ar[i]);i--;}
}
int main()
{unsigned int n = 0;scanf("%d", &n);Show(n);
}
法二:递归法
void Show(unsigned int n)
{if (n == 0) return;else{Show(n / 10);printf("%d", n % 10);}
}
int main()
{unsigned int n = 0;scanf("%d", &n);Show(n);
}
4.计算第n位Fibonacci数列
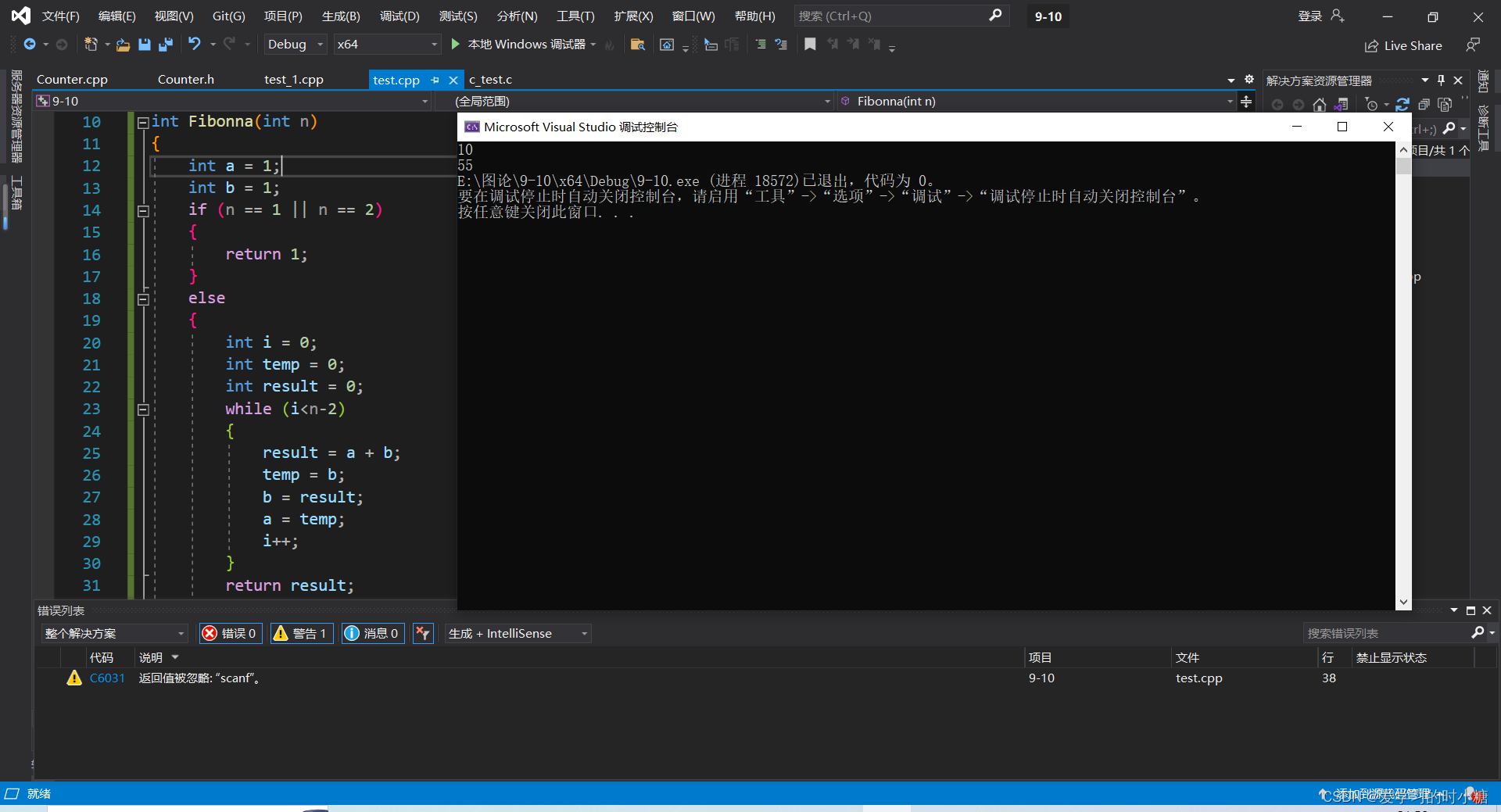
法一:循环输出
int Fibonna(int n)
{int a = 1;int b = 1;if (n==0) return 0;if (n == 1 || n == 2){return 1;}else{int i = 0;int temp = 0;int result = 0;while (i<n-2){result = a + b;temp = b;b = result;a = temp;i++;}return result;}}
int main()
{int n = 0;scanf("%d", &n);int result = Fibonna(n);printf("%d", result);
}
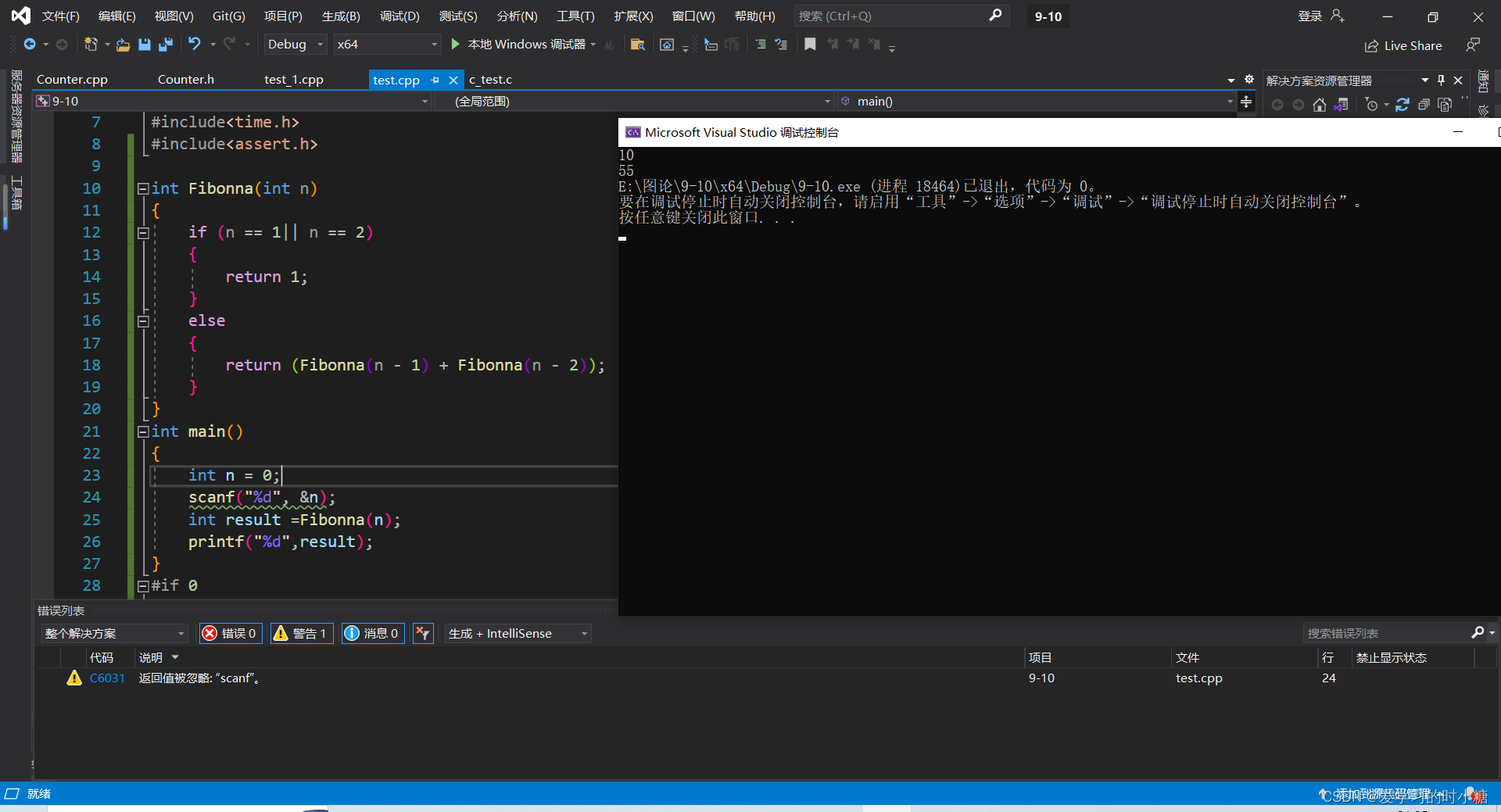
法二:递归输出
int Fibonna(int n)
{if (n == 0) return 0;if (n == 1|| n == 2){return 1;}else{return (Fibonna(n - 1) + Fibonna(n - 2));}
}
int main()
{int n = 0;scanf("%d", &n);int result =Fibonna(n);printf("%d",result);
}
Q: 使用递归进行输出的时候空间复杂度是2^n,很大,怎么样降低时间复杂度?
A: 想要降低复杂度,主要就是要减少一个递归函数,将递归过程中的值存储下来就能减少相应的复杂程度。
写法一:一定要注意a,b,temp不能每次被调用的时候都初始化,要不然输出的值不正确。
int fac(int n)
{static int a = 1;static int b = 1;static int temp = 1;if (n <= 2) return temp;temp = a + b;b = a;a = temp;fac(n - 1);
}
int main()
{int n = 0;scanf("%d", &n);int result = fac(n);printf("%d", result);
}
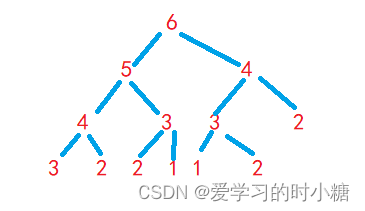
写法二:思路一致,只不过老师写的更清楚明了。
int fanc(int n, int a, int b)
{if (n <= 2) return a;else return fanc(n - 1, a + b, a);
}
int fac(int n)
{int a = 1;int b = 1;return fanc(n, a, b);
}
int main()
{int n = 0;scanf("%d", &n);int result = fac(n);printf("%d", result);
} 5.无序整数数组打印
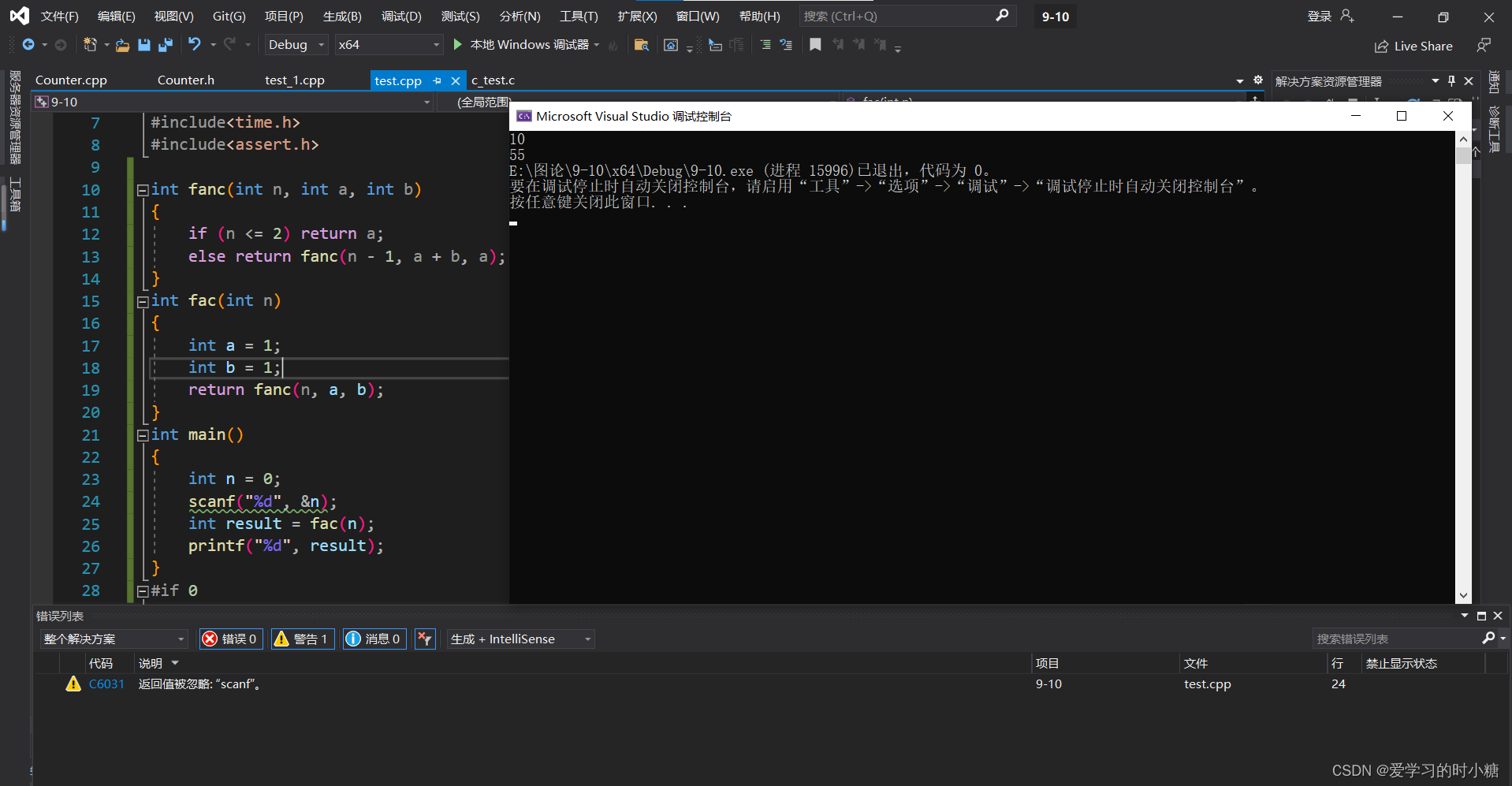
5.无序整数数组打印
有一个整型数组,数值无序,使用循环和递归打印和查询。
法一:循环打印
void Show_Arr(const int* ar, const int n)
{if (n < 1 || ar == NULL) return;for (int i = 0; i < n; i++){printf("%d ", ar[i]);}
}
int main()
{const int n = 3;int ar[n] = { 12,23,34 };Show_Arr(ar,n);
} 法二:使用递归打印数组
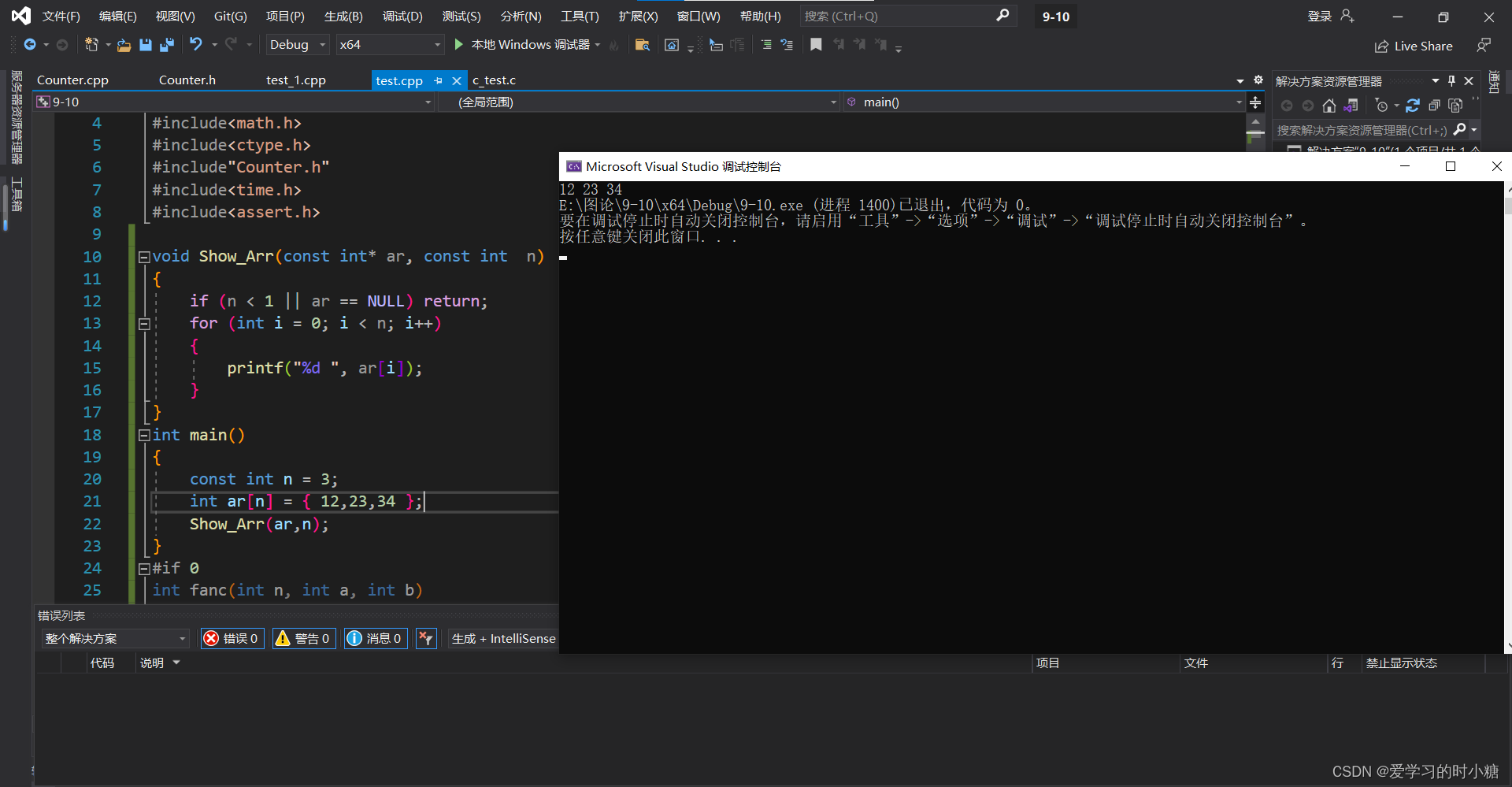
法二:使用递归打印数组
void Show_Arr(const int* ar, const int n)
{if (n < 1 || ar == NULL) return;Show_Arr(ar, n - 1);printf("%d ", ar[n - 1]);}
int main()
{const int n = 3;int ar[n] = { 12,23,34 };Show_Arr(ar, n);
}
Q:上述递归代码我可可以将n-1修改成n--吗?请详细说明。
A:不可以修改,后置--是先取值后--,在下面示例中,n=3,n>0,调用函数,调用的新的函数还是n=3的函数,进入到一个循环,直到栈帧空间被填满。

Q:上述递归代码我可可以将n-1修改成--n吗?请详细说明。
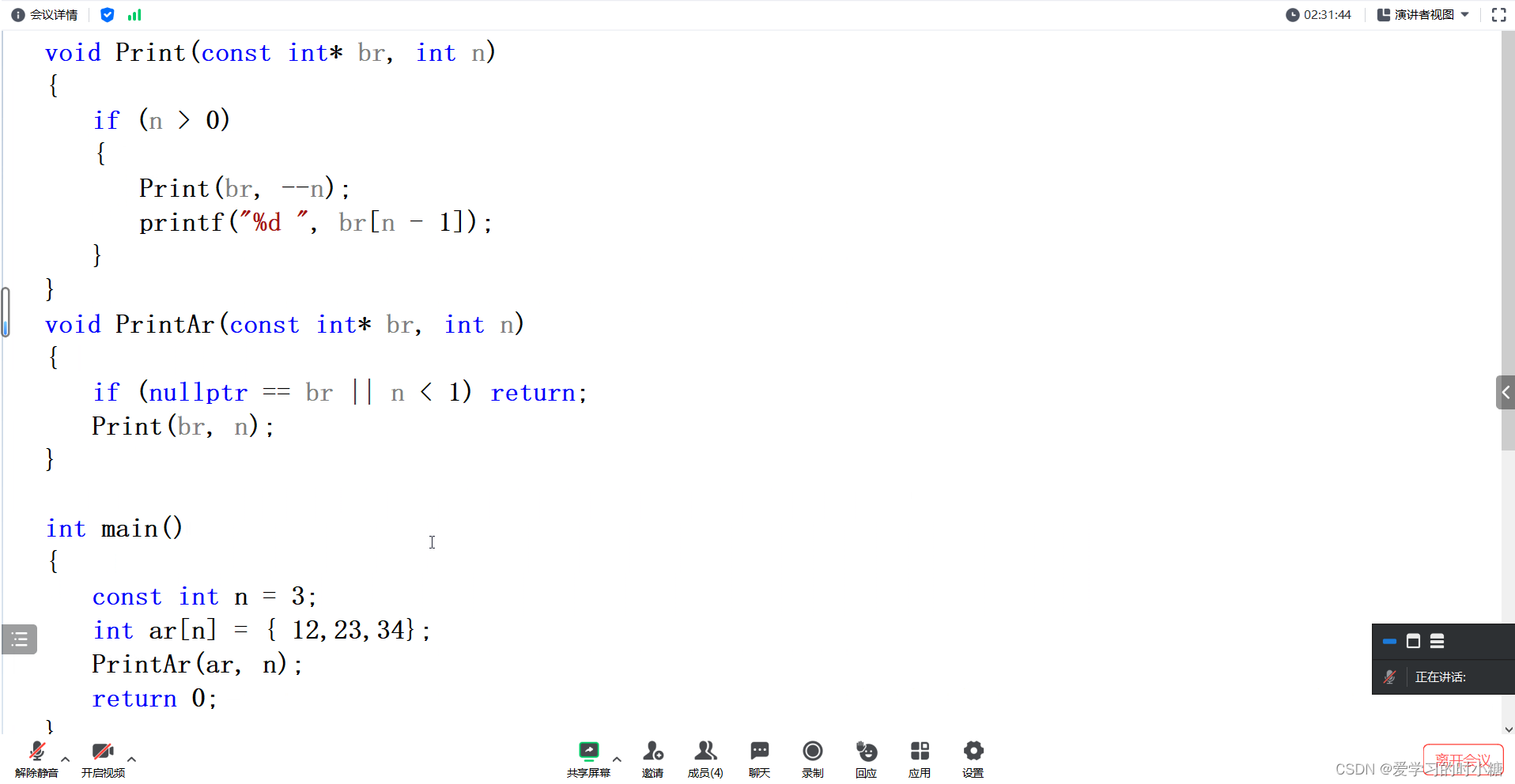
A:也不可以修改,前置--是先--再取值,的确可以满足递归调用的逻辑,但是当他进行回归的时候会n的值被更改了,输出的是更改后的n-1,造成数据溢出问题。

6.找到对应数组下标
法一:循环找数组下标
int FindValue(const int* arr, int n, int value)
{if (n < 1 || arr == NULL) return 0;int pos = -1;for (int i = 0; i < n; i++){if (arr[i] == value){pos = i;break;}}return pos;
}
int main()
{const int n = 5;int arr[n] = { 10,11,12,13,14 };int val = 0;scanf("%d", &val);int m = FindValue(arr, n, val);printf("%d", m);
}
法二:递归找数组下标
这面这个代码输出的数组下标有问题,一直是-1
int FindValue(const int* br, int n, int val)
{int pos = -1;if (NULL == br || n < 1) return pos;if (br[n-1] == val){pos = n - 1;}else{FindValue(br, n - 1, val);}return pos;
}
int main()
{const int n = 5;int arr[n] = { 10,11,12,13,14 };int val = 0;scanf("%d", &val);int m=FindValue(arr,n,val);printf("%d", m);
}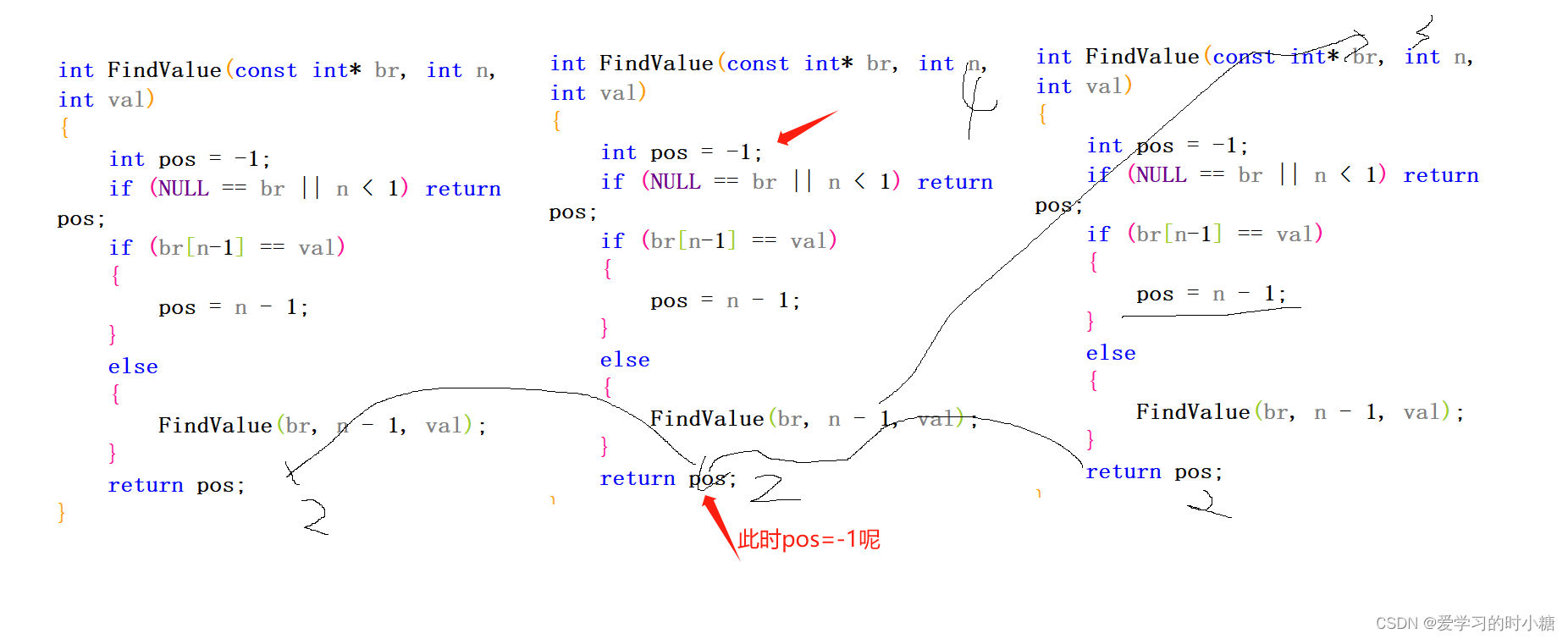
正确代码
int FindValue(const int* br, int n, int val)
{int pos = -1;if (NULL == br || n < 1) return pos;if (br[n-1] == val){pos = n - 1;}else{pos =FindValue(br, n - 1, val);}return pos;
}
int main()
{const int n = 5;int arr[n] = { 10,11,12,13,14 };int val = 0;scanf("%d", &val);int m=FindValue(arr,n,val);printf("%d", m);
}
相关文章:

C语言第入门——第十六课
目录 一、分治策略与递归 二、递归 1.求解n的阶乘 2.输入整数、倒序输出 3.输入整数、正序输出 4.计算第n位Fibonacci数列 编辑5.无序整数数组打印 6.找到对应数组下标 一、分治策略与递归 在我们遇到大问题的时候,我们的正确做法是将它分解成小问题&a…...

IntelliJ IDEA 快捷键 Windows 版本
前言:常用快捷键 IntelliJ IDEA编辑器大受欢迎的原因之一是它的智能提示和丰富的快捷键,在日常开发中熟练的使用快捷键会大大提升开发的效率,本篇文章就笔者日常开发中的总结,把常用的、好用的快捷键做一个列表,方便…...

重生之我必去大厂java开发
JavaDreamer 重生之我必去大厂java开发。主线任务进入大厂java开发。 author :developer_zxh GitHub | Gitee 本项目记录了本人从中国科学院大学硕士研究生开始,如何进入大工 java 开发岗位的学习记录(目前在校未求职,加入后此状…...
2023年中职“网络安全“—Web 渗透测试②
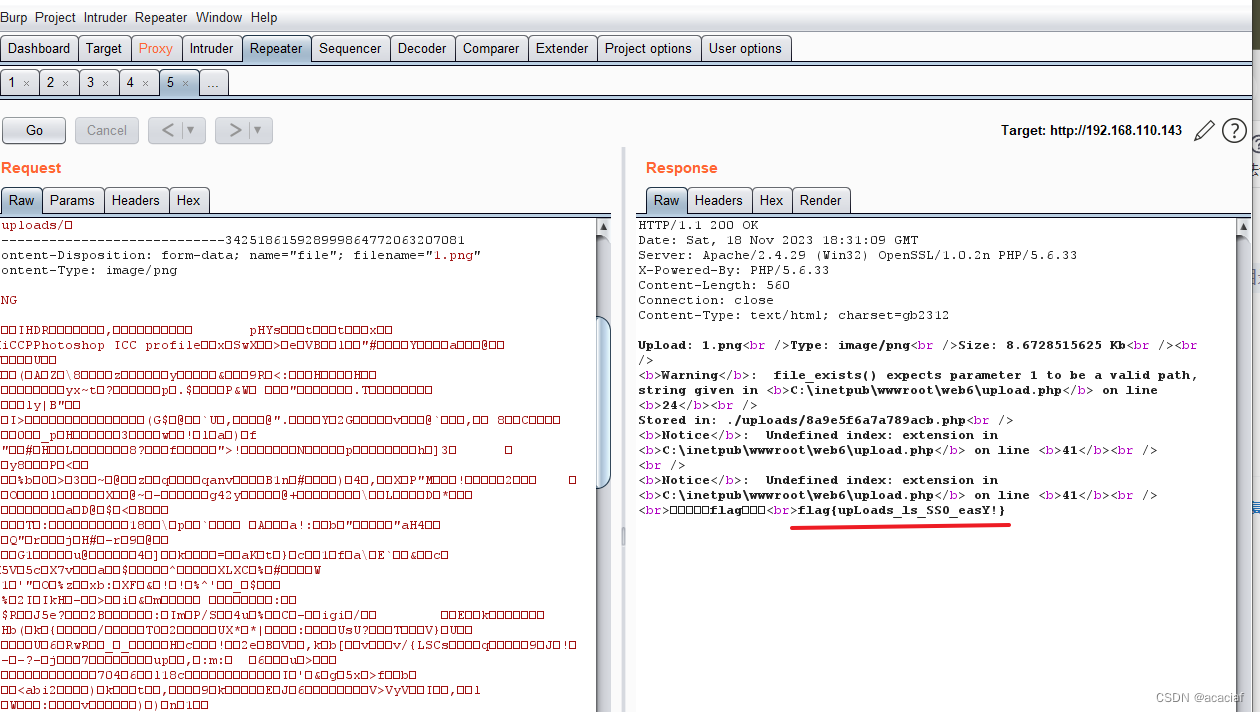
2023年中职“网络安全“—Web 渗透测试② Web 渗透测试任务环境说明:1.访问http://靶机IP/web1/,获取flag值,Flag格式为flag{xxx};2.访问http://靶机IP/web2/,获取flag值,Flag格式为flag{xxx};3.访问http://靶机IP/web…...
【整顿C盘】pycharm、chrome等软件,缓存移动
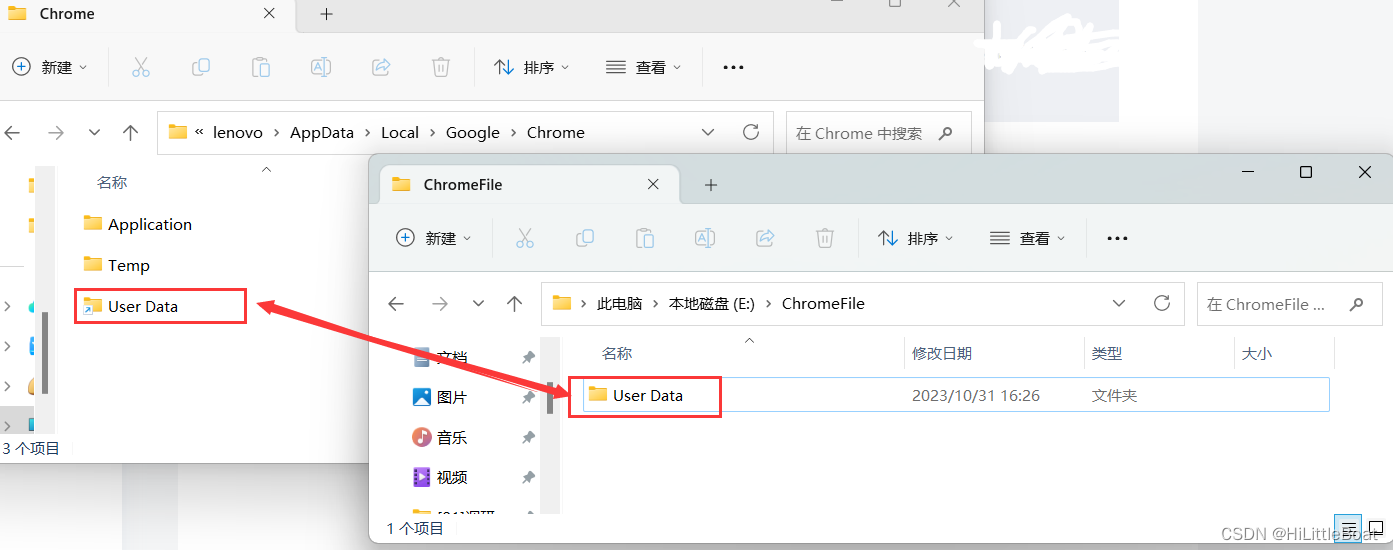
C盘爆了,特来找一下巨大的软件缓存,特此记录,跟随的各大教程,和自己的体会 一、爆炸家族JetBrains 这个适用于pycharm、idea、webstorm等等,只要是JetBrains家的,2020版本以上,都是一样的方法 p…...

C# using语句使用介绍
在C#中,using语句有两种主要用途:一是引入命名空间,二是提供一种简便的方式来处理资源的清理(主要用于实现了 IDisposable 接口的对象)。 引入命名空间:using 语句用于引入命名空间,从而可以在代…...
 201. 数字范围按位与 (位运算))
leetcode (力扣) 201. 数字范围按位与 (位运算)
文章目录 题目描述思路分析完整代码 题目描述 给你两个整数 left 和 right ,表示区间 [left, right] ,返回此区间内所有数字 按位与 的结果(包含 left 、right 端点)。 示例 1: 输入:left 5, right 7 输出…...
Flutter笔记: 在Flutter应用中使用SQLite数据库
Flutter笔记 在Flutter应用中使用SQLite数据库(基于sqflite) 作者:李俊才 (jcLee95):https://blog.csdn.net/qq_28550263 邮箱 :291148484163.com 本文地址:https://blog.csdn.net/q…...
OpenAI GPT5计划泄露
OpenAI的首席执行官萨姆奥特曼在最近接受《金融时报》的专访时,分享了OpenAI未来发展的一些新动向。此外,他还透露了关于即将到来的GPT-5模型以及公司对AGI的长期目标的一些细节。 奥特曼指出: 1.OpenAI正在开发GPT-5,一种更先进的…...

【面试经典150 | 数学】Pow(x, n)
文章目录 写在前面Tag题目来源题目解读解题思路方法一:快速幂-递归方法二:快速幂-迭代 其他语言python3 写在最后 写在前面 本专栏专注于分析与讲解【面试经典150】算法,两到三天更新一篇文章,欢迎催更…… 专栏内容以分析题目为主…...

封装比较好的登录页面
封装比较好的登录页面 只在setup()函数中写流程,将逻辑代码抽离出来 <template><div class"wrapper"><img class"wrapper__img" srchttp://www.dell-lee.com/imgs/vue3/user.png /><div class"wrapper__input"&…...

如何使用Flask request对象处理请求
在 Flask 中,request 对象是处理 HTTP 请求的重要工具之一。它提供了许多属性和方法,可以帮助我们获取请求的相关信息和数据。本文将向你介绍 request 对象的常用方法以及如何在 Flask 应用程序中使用它。 1. 获取请求方法 首先,让我们看一…...
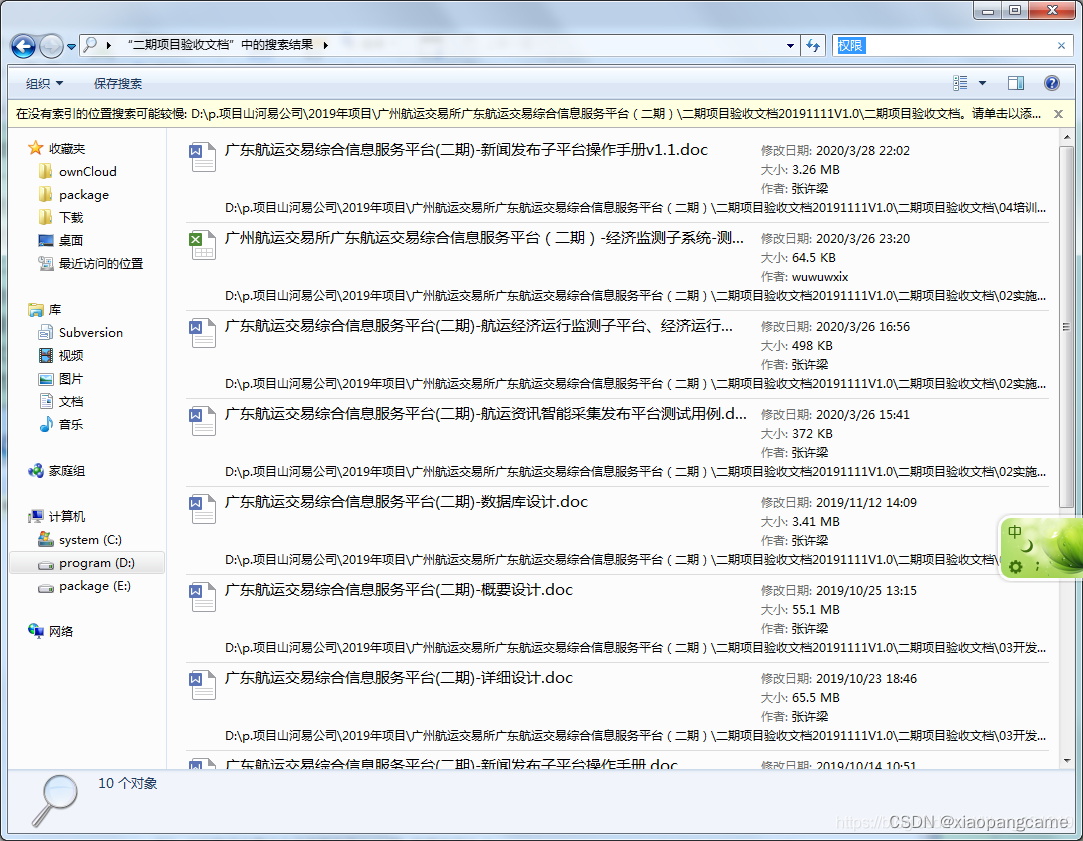
快速搜索多个word、excel等文件中内容
如何快速搜索多个word、excel等文件中内容 操作方法 以win11系统为介绍对象。 首先我们打开“我的电脑”-->“文件夹选项”-->“搜索”标签页,在“搜索内容”下方选择:"始终搜索文件名和内容(此过程可能需要几分钟)"。然后…...
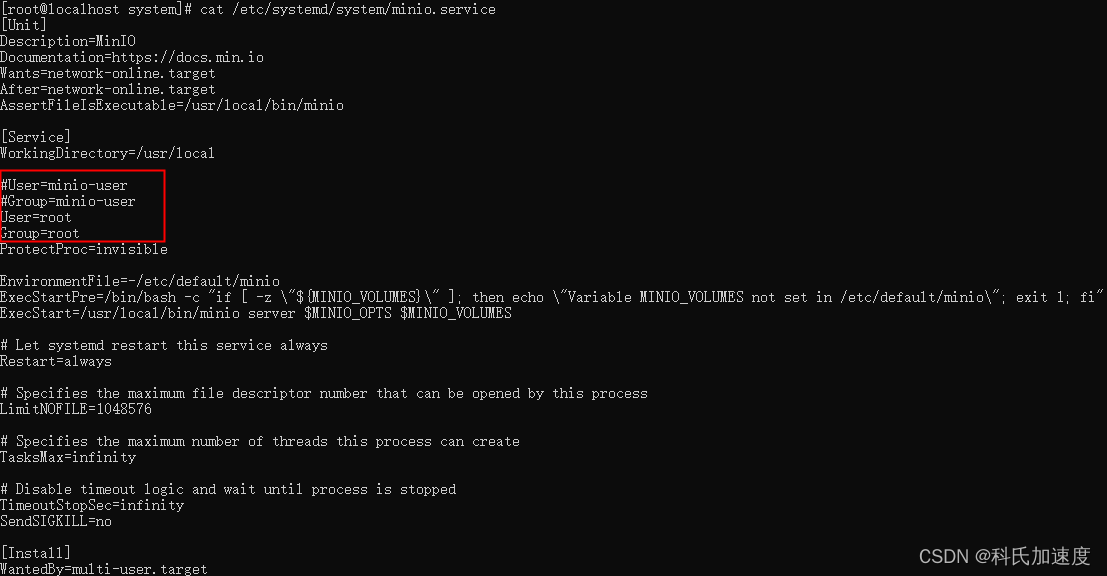
Minio安装
环境 centos8,关闭防火墙 minio-20231101183725版本 参考官网:部署 MinIO:单节点单硬盘 — 适用于 Linux 的 MinIO 对象存储 单例 下载rpm,用中国镜像 wget https://dl.minio.org.cn/server/minio/release/linux-amd64/arch…...
Spring初识
未来的几周时间,大概率我会更新一下Spring家族的一些简单知识。而什么是Spring家族,好多同学还不是很清楚,我先来简单介绍一下吧: 所谓Spring家族,它其实就是一个框架,是基于Servlet再次进行封装的内容。为…...

2023全新付费进群系统源码 带定位完整版 附教程
这源码是我付费花钱买的分享给大家,功能完整。 搭建教程 Nginx1.2 PHP5.6-7.2均可 最好是7.2 第一步上传文件程序到网站根目录解压 第二步导入数据库(58soho.cn.sql) 第三步修改/config/database.php里面的数据库地址 第四步修改/conf…...

C# LINQ使用介绍
LINQ(Language-Integrated Query)是C#语言的一个强大特性,它允许开发者用声明性的方式查询和操作数据。LINQ提供了一致的查询体验,无论是操作内存中的对象(如数组或集合),还是操作外部数据源&am…...

【c++】——类和对象(中)——实现完整的日期类(优化)万字详细解疑答惑
作者:chlorine 专栏:c专栏 赋值运算符重载()()():实现完整的日期类(上) 我走的很慢,但我从不后退。 【学习目标】 日期(- - --)天数重载运算符 日期-日期 返回天数 对日期类函数进行优化(不符合常理的日期,负数,const成员)c中重载输入cin和输…...

开源与闭源:大模型时代的技术交融与商业平衡
一、开源和闭源的优劣势比较 1.1 开源 优势: 1.技术共享与吸引人才: 开源促进了技术共享,吸引了全球范围内的人才参与大模型的发展,形成了庞大的开发者社区。 2.推动创新: 开源模式鼓励开发者共同参与,推动…...

C#开发的OpenRA游戏之属性BodyOrientation(6)
C#开发的OpenRA游戏之属性BodyOrientation(6) 在顶层定义里会发现这个属性: ^SpriteActor: BodyOrientation: QuantizeFacingsFromSequence: RenderSprites: SpriteActor是用来定义角色的基本属性,它的第一个属性就是BodyOrientation,这个属性主要用来描述角色的身体的…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...
