【C++进阶】三、二叉搜索树
目录
一、二叉搜索树
1.1 概念
1.2 二叉搜索树操作
二、二叉搜索树实现
2.1 框架总览
2.2 实现接口总览
2.2.1 构造函数
2.2.2 拷贝构造
2.2.3 赋值重载
2.2.4 析构函数
2.2.5 二叉搜索树的遍历
2.2.6 插入函数
2.2.7 查找函数
2.2.8 删除函数
2.3 二叉搜索数完整代码
三、二叉搜索树的应用
3.1 K模型
3.2 KV模型
四、二叉搜索树的性能分析
前言:二叉搜索树是数据结构初阶二叉树的一部分,二叉搜索树为后序所学的 map 和 set 做准备
一、二叉搜索树
1.1 概念
二叉搜索树(BST,Binary Search Tree)又称二叉排序树,它或者是一棵空树,二叉树搜索树具有以下性质:
- 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
- 若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
- 它的左右子树也分别为二叉搜索树
比如,下面就是一颗二叉搜索树
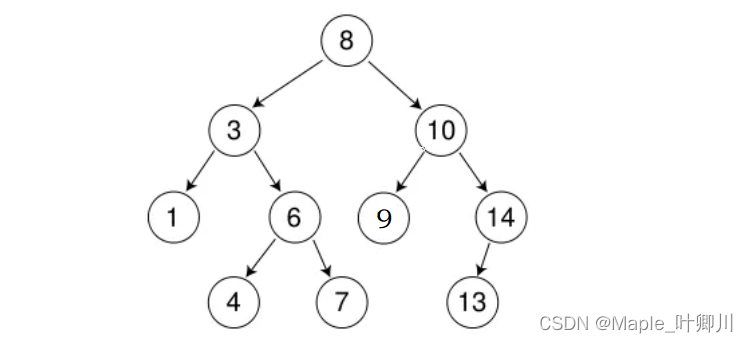
左子树小于根节点,右子树大于根节点,每颗子树都保持这样的特性,这样的树就称为二叉搜索树
二叉搜索树进行中序遍历,遍历出来的结果是有序的(升序),二叉搜索树一般都是去重的,即没有相同的值
1.2 二叉搜索树操作
二叉搜索树的主要接口就是插入、查找、删除、遍历
(1)查找(Find)
- 从根开始比较,查找,比根大则往右边走查找,比根小则往左边走查找
- 最多查找高度次,走到到空,还没找到,这个值不存在
(2)插入(Insert)
插入一个节点,插入后保持二叉搜索树的性质,二叉搜索树实现下面解释
(3)删除(Erase)
删除一个节点,删除后保持二叉搜索树的性质,二叉搜索树实现下面解释
(4)遍历(InOrder)
使用中序遍历即可,遍历结果为升序序列
二、二叉搜索树实现
2.1 框架总览
要实现二叉搜索树,我们首先需要实现一个节点类,结点类当中包含三个成员变量:结点的值、左指针、右指针,结点类当中只需实现一个构造函数即可
二叉搜索树类(BSTree)里面的成员变量只要包含一个根节点 _root 即可
为了书写简单,对 BSTreeNode<K> 进行 typedef 为 Node
typedef BSTreeNode<K> Node
template<class K>
struct BSTreeNode
{BSTreeNode(const K& key):_key(key), _left(nullptr), _right(nullptr){}K _key;BSTreeNode<K>* _left;BSTreeNode<K>* _right;
};template<class K>
class BSTree
{typedef BSTreeNode<K> Node;
public:private:Node* _root;
};2.2 实现接口总览
template<class K>
struct BSTreeNode
{BSTreeNode(const K& key):_key(key), _left(nullptr), _right(nullptr){}K _key;BSTreeNode<K>* _left;BSTreeNode<K>* _right;
};template<class K>
class BSTree
{typedef BSTreeNode<K> Node;
public://构造函数BSTree(){}//拷贝构造BSTree(const BSTree<K>& t){}//赋值重载BSTree<K>& operator=(BSTree<K> t){}//析构~BSTree(){}bool Insert(const K& key){}bool Find(const K& key){}bool Erase(const K& key){}//遍历搜索树void InOrder(){}private:Node* _root;
};2.2.1 构造函数
构造函数非常简单,构造一个空树即可
//构造函数BSTree():_root(nullptr){}2.2.2 拷贝构造
由于要进行递归操作,就不能把递归操作写在拷贝构造函数里面,需要另写一个函数,这个函数设置为私有,拷贝构造也是深拷贝
//拷贝构造
BSTree(const BSTree<K>& t)
{_root = Copy(t._root);
}private:Node* Copy(Node* root){if (root == nullptr){return nullptr;}Node* newRoot = new Node(root->_key);newRoot->_left = Copy(root->_left);newRoot->_right = Copy(root->_right);return newRoot;}2.2.3 赋值重载
赋值重载直接使用现代写法,复用拷贝构造,不解释了,赋值重载也是深拷贝
//赋值重载
BSTree<K>& operator=(BSTree<K> t)
{swap(_root, t._root);return *this;
}2.2.4 析构函数
析构函数也是如此,需要进行递归操作,需要另写一个函数进行递归操作
//析构
~BSTree()
{Destroy(_root);_root = nullptr;
}private:void Destroy(Node* root){if (root == nullptr){return;}Destroy(root->_left);Destroy(root->_right);delete root;}2.2.5 二叉搜索树的遍历
遍历使用中序遍历即可,遍历出来的结果是升序的,因为无法使用类成员变量,就无法传根进行递归遍历,所以也需要另写一个函数
代码如下:
//遍历搜索树
void InOrder()
{_InOrder(_root);cout << endl;
}private:void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}2.2.6 插入函数
根据二叉搜索树的性质,其插入操作非常简单:
- 如果是空树,则直接将插入结点作为二叉搜索树的根结点
- 如果不是空树,则按照二叉搜索树的性质进行结点的插入
若不是空树,插入结点的具体操作如下:
- 若待插入结点的值小于根结点的值,则需要将结点插入到左子树当中
- 若待插入结点的值大于根结点的值,则需要将结点插入到右子树当中
- 若待插入结点的值等于根结点的值,则插入结点失败(二叉搜索树)
插入成功返回 true,插入失败返回 false
代码如下:
bool Insert(const K& key){//_root为空树if (_root == nullptr){_root = new Node(key);return true;}//不为空树,进行查找Node* parent = nullptr;Node* cur = _root;while (cur)//遇到空就结束{if (_root->_key > key)//在左子树{parent = cur;cur = cur->_left;}else if (_root->_key < key)//在右子树{parent = cur;cur = cur->_right;}else//相等,直接返回,不允许插入相同值{return false;}}cur = new Node(key);if (parent->_key > key)//parent节点的_key比key大,插入到左边{parent->_left = cur;}else//parent节点的_key比key小,插入到右边{parent->_right = cur;}return true;}2.2.7 查找函数
根据二叉搜索树的特性,,分以下几种情况:
- 若树为空树,则查找失败,返回 false
- 若key值小于当前结点的值,则应该在该结点的左子树当中进行查找
- 若key值大于当前结点的值,则应该在该结点的右子树当中进行查找
- 若key值等于当前结点的值,则查找成功,返回 true
- 查找完了,还是没有找到,返回 false
代码如下:
bool Find(const K& key){Node* cur = _root;while (cur){if (cur->_key > key){cur = cur->_left;}else if (cur->_key < key){cur = cur->_right;}else//找到了{return true;}}//空树或者找不到return false;}2.2.8 删除函数
二叉搜索树的删除函数是最难实现的,若是在二叉树当中没有找到待删除结点,则直接返回 false 表示删除失败即可,但若是找到了待删除结点,此时就有以下三种情况:
- 待删除结点的左子树为空
- 待删除结点的右子树为空
- 待删除结点的左右子树均不为空
下面进行一对一处理:
(1)待删除结点的左子树为空,即右子树不为空
若待删除结点的左子树为空,那么当我们在二叉搜索树当中找到该结点后,只需先让其父结点指向该结点的右孩子结点,然后再将该结点释放便完成了该结点的删除,进行删除操作后仍保持二叉搜索树的特性
动图演示:
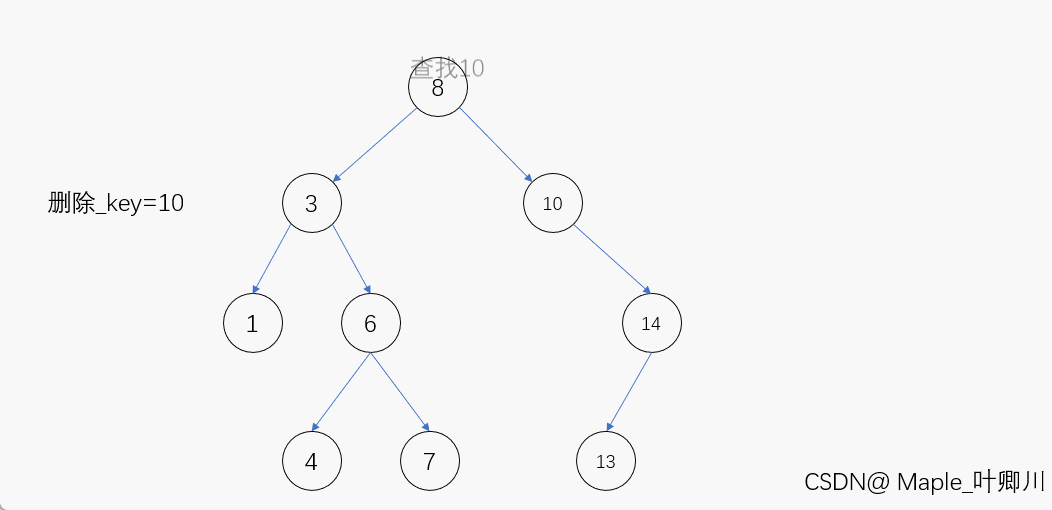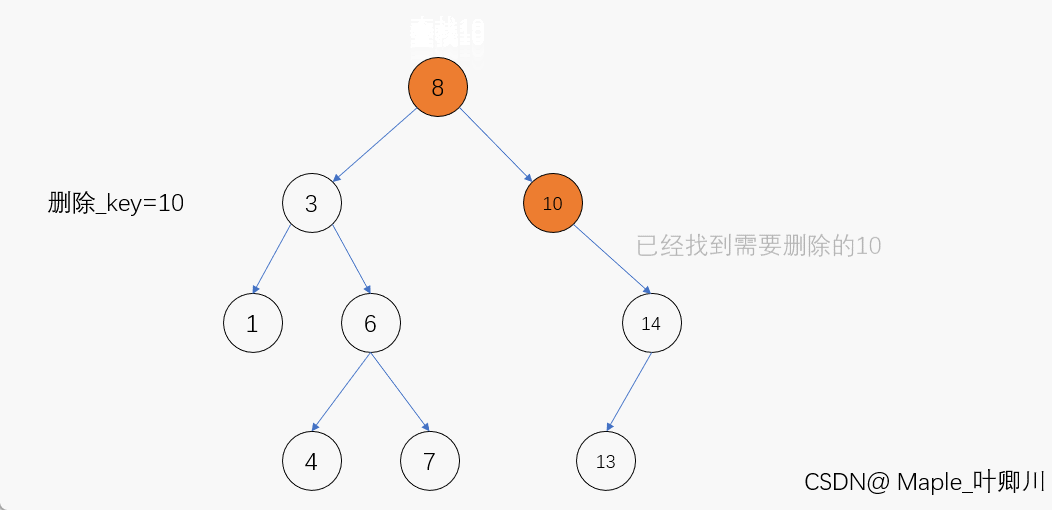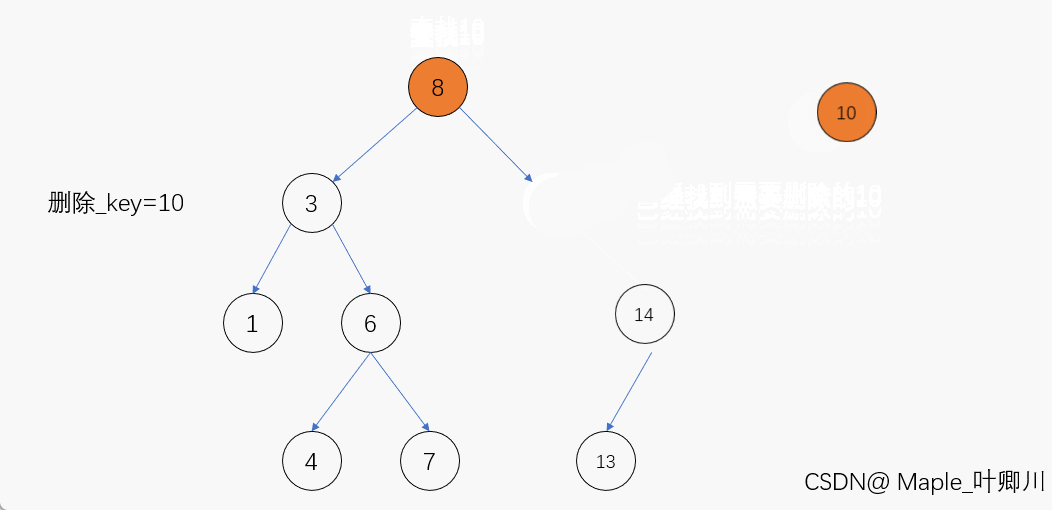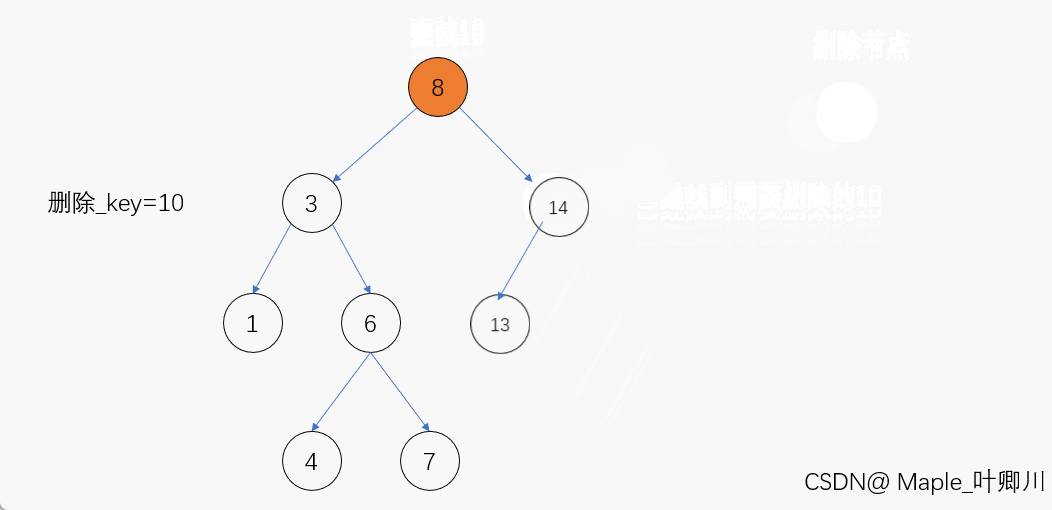
(2)待删除结点的右子树为空,即左子树不为空
若待删除结点的右子树为空,那么当我们在二叉搜索树当中找到该结点后,只需先让其父结点指向该结点的左孩子结点,然后再将该结点释放便完成了该结点的删除,进行删除操作后仍需要保持二叉搜索树的特性
动图演示:
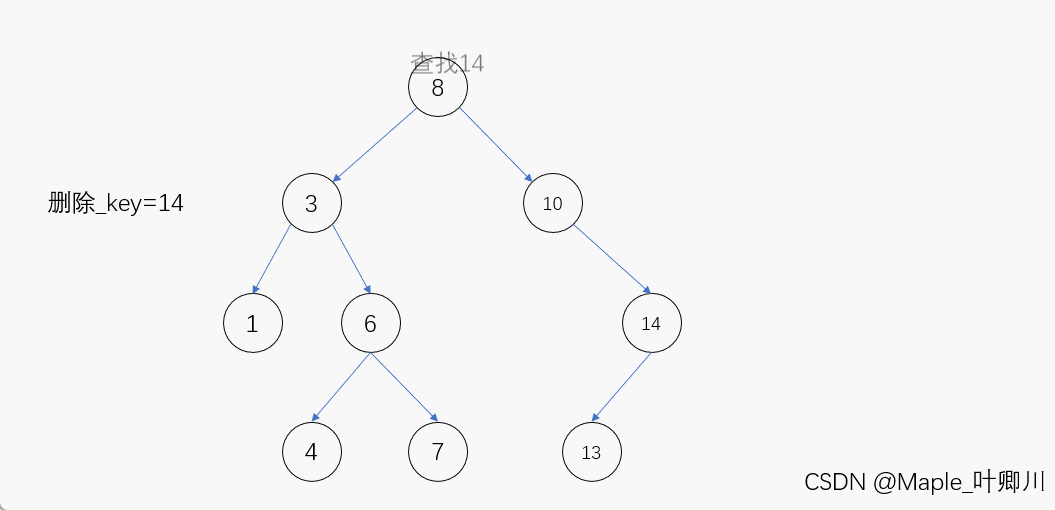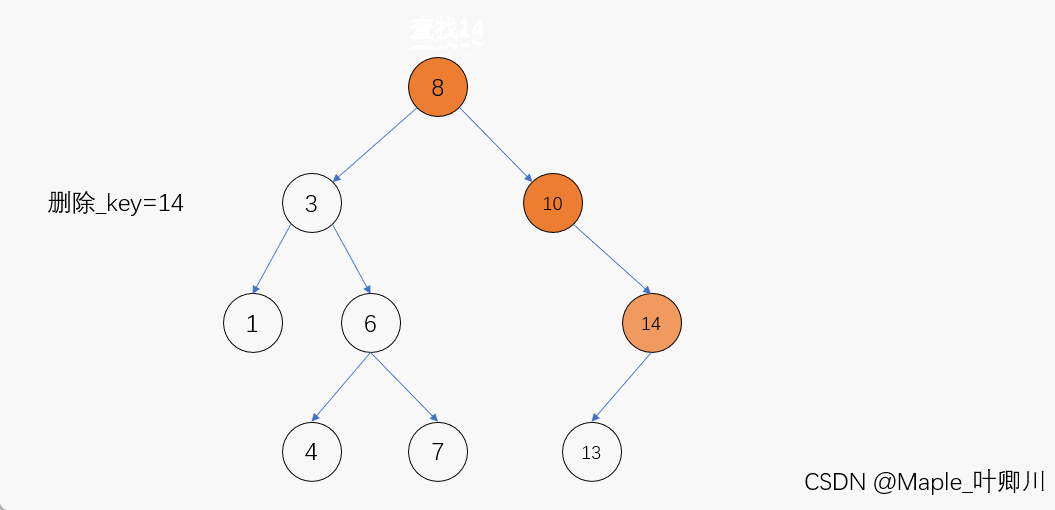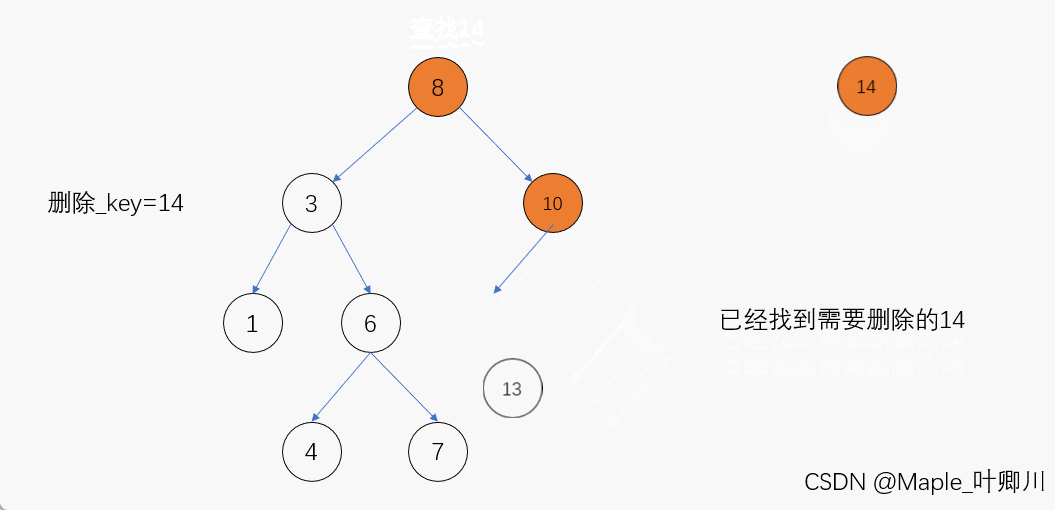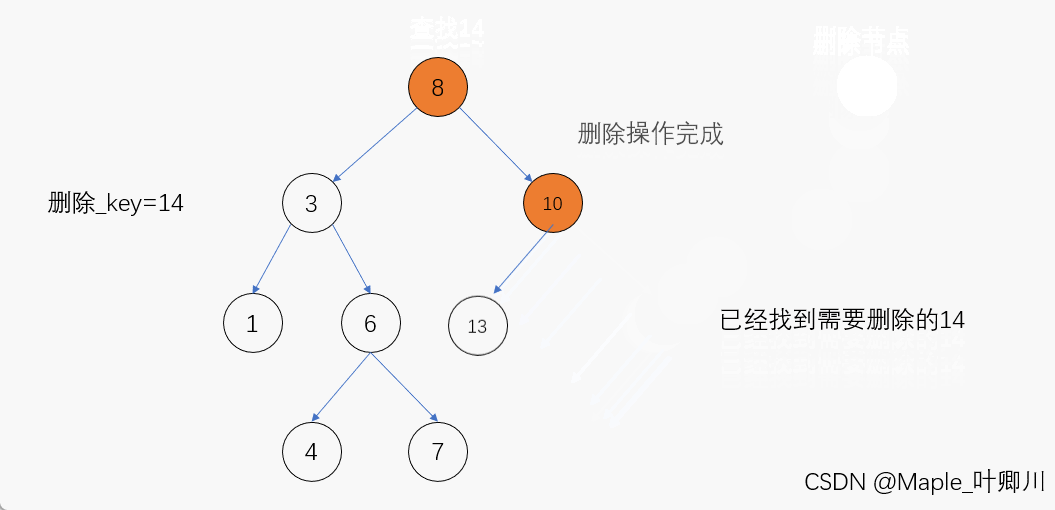
(3)待删除结点的左右子树均不为空
若待删除结点的左右子树均不为空,那么当我们在二叉搜索树当中找到该结点后,可以使用替换法进行删除
有两种替换方法:可以将让待删除结点左子树当中值最大的结点,或是待删除结点右子树当中值最小的结点代替待删除结点被删除(下面都以最小的结点代替待删除为例)
然后将待删除结点的值改为代替其被删除的结点的值即可,而代替待删除结点被删除的结点,必然左右子树当中至少有一个为空树,因此删除该结点的方法与前面说到的情(1)(2)的方法相同
注意:只能是待删除结点左子树当中值最大的结点,或是待删除结点右子树当中值最小的结点代替待删除结点被删除,因为只有这样才能使得进行删除操作后的二叉树仍保持二叉搜索树的特性
动图演示:
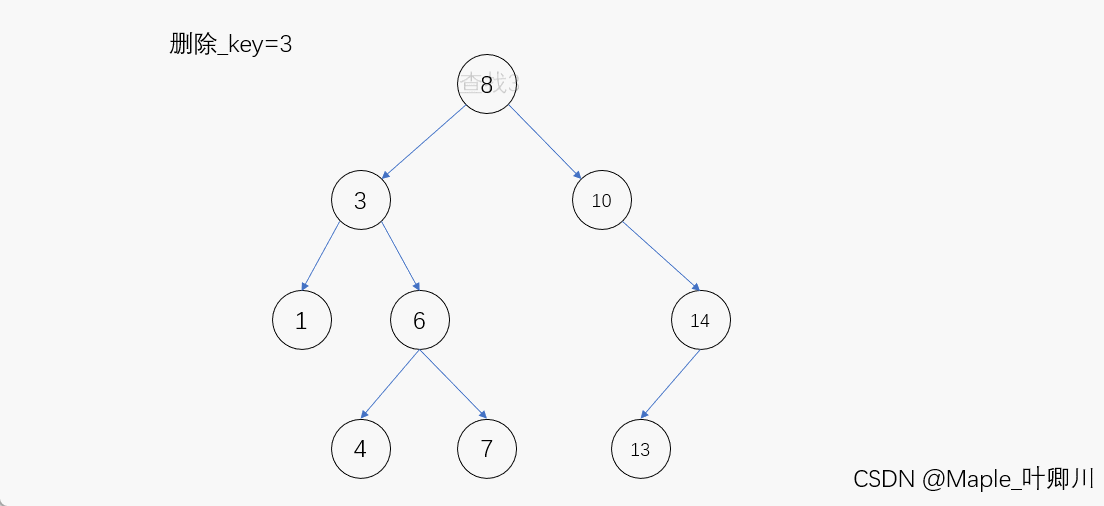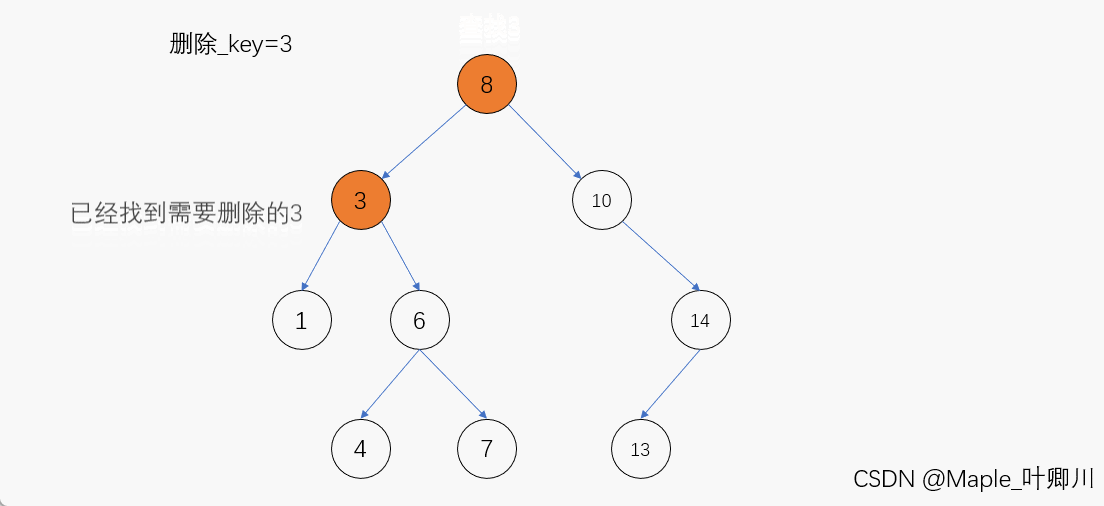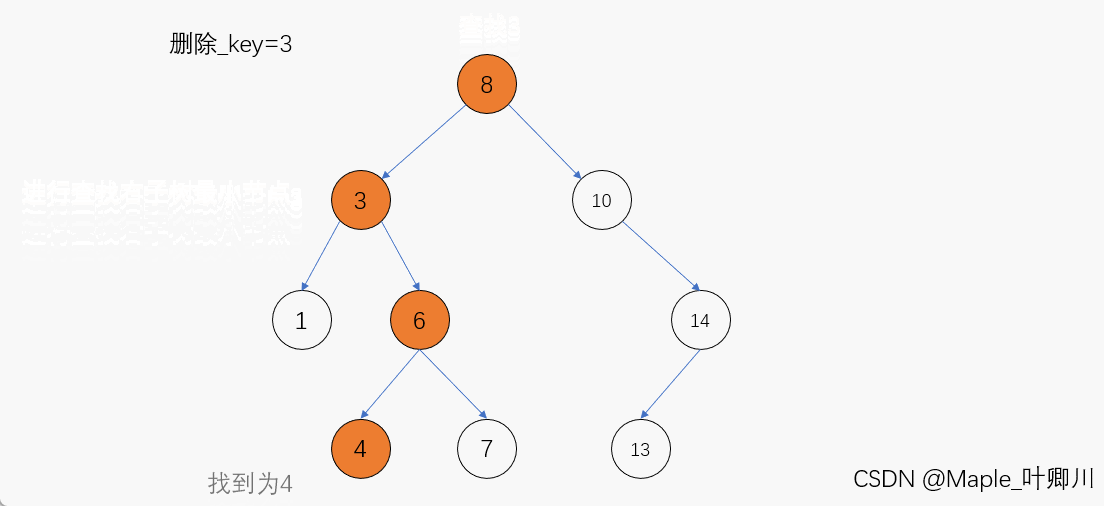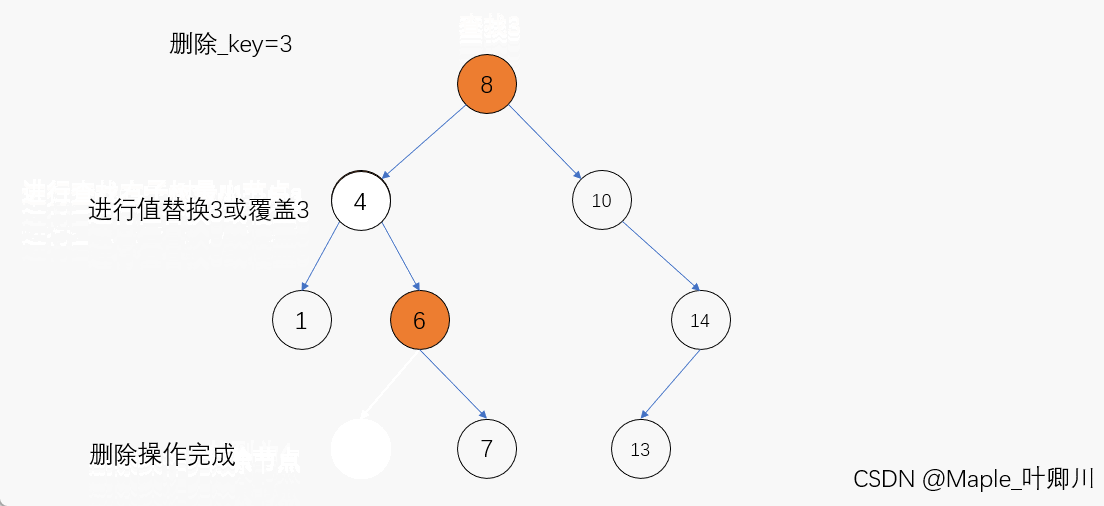
代码如下:
bool Erase(const K& key)
{Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key > key){parent = cur;cur = cur->_left;}else if (cur->_key < key){parent = cur;cur = cur->_right;}else//找到了要删除的节点{//左为空,右不为空if (cur->_left == nullptr){if (cur == _root)//要删除的为根节点{_root = cur->_right;}else//非根节点{parent->_right = cur->_right;}delete cur;}else if (cur->_right == nullptr)//左不为空,右为空{if (cur == _root)//要删除的为根节点{_root = cur->_left;}else//非根节点{parent->_left = cur->_left;}delete cur;}else//左右不为空,替换删除{//左右不为空,需要左子树的最大值 或 右子树的左小值充当新的根(对被删除节点进行值替换,然后进行删除)Node* minParent = cur;Node* minRight = cur->_right;//这里选用最小值进行替换while (minRight->_left){minParent = minRight;minRight = minRight->_left;}cur->_key = minRight->_key;//值替换,minRight换不换没影响,minRight是要被删除的//分两种情况if (minRight == minParent->_left){minParent->_left = minRight->_right;}else{minParent->_right = minRight->_right;}delete minRight;}return true;}}return false;
}2.3 二叉搜索数完整代码
BSTree.h
#pragma oncetemplate<class K>
struct BSTreeNode
{BSTreeNode(const K& key):_key(key), _left(nullptr), _right(nullptr){}K _key;BSTreeNode<K>* _left;BSTreeNode<K>* _right;
};template<class K>
class BSTree
{typedef BSTreeNode<K> Node;
public://构造函数BSTree():_root(nullptr){}//拷贝构造BSTree(const BSTree<K>& t){_root = Copy(t._root);}//赋值重载BSTree<K>& operator=(BSTree<K> t){swap(_root, t._root);return *this;}//析构~BSTree(){Destroy(_root);_root = nullptr;}bool Insert(const K& key){//_root为空树if (_root == nullptr){_root = new Node(key);return true;}//不为空树,进行查找Node* parent = nullptr;Node* cur = _root;while (cur)//遇到空就结束{if (_root->_key > key)//在左子树{parent = cur;cur = cur->_left;}else if (_root->_key < key)//在右子树{parent = cur;cur = cur->_right;}else//相等,直接返回,不允许插入相同值{return false;}}cur = new Node(key);if (parent->_key > key)//parent节点的_key比key大,插入到左边{parent->_left = cur;}else//parent节点的_key比key小,插入到右边{parent->_right = cur;}return true;}bool Find(const K& key){Node* cur = _root;while (cur){if (cur->_key > key){cur = cur->_left;}else if (cur->_key < key){cur = cur->_right;}else//找到了{return true;}}//空树或者找不到return false;}bool Erase(const K& key){Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key > key){parent = cur;cur = cur->_left;}else if (cur->_key < key){parent = cur;cur = cur->_right;}else//找到了要删除的节点{//左为空,右不为空if (cur->_left == nullptr){if (cur == _root)//要删除的为根节点{_root = cur->_right;}else//非根节点{parent->_right = cur->_right;}delete cur;}else if(cur->_right == nullptr)//左不为空,右为空{if (cur == _root)//要删除的为根节点{_root = cur->_left;}else//非根节点{parent->_left = cur->_left;}delete cur;}else//左右不为空,替换删除{//左右不为空,需要左子树的最大值 或 右子树的左小值充当新的根(对被删除节点进行值替换,然后进行删除)Node* minParent = cur;Node* minRight = cur->_right;//这里选用最小值进行替换while (minRight->_left){minParent = minRight;minRight = minRight->_left;}cur->_key = minRight->_key;//值替换,minRight换不换没影响,minRight是要被删除的//分两种情况if (minRight == minParent->_left){minParent->_left = minRight->_right;}else{minParent->_right = minRight->_right;}delete minRight;}return true;}}return false;}//遍历搜索树void InOrder(){_InOrder(_root);cout << endl;}
private:void Destroy(Node* root){if (root == nullptr){return;}Destroy(root->_left);Destroy(root->_right);delete root;}Node* Copy(Node* root){if (root == nullptr){return nullptr;}Node* newRoot = new Node(root->_key);newRoot->_left = Copy(root->_left);newRoot->_right = Copy(root->_right);return newRoot;}void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}
private:Node* _root;
};Test.cpp
#include <iostream>
using namespace std;#include "BSTree.h"void Test()
{BSTree<int> t;t.Insert(4);t.Insert(3);t.Insert(5);t.Insert(4);t.Insert(6);t.Insert(1);t.Insert(7);t.Insert(9);t.InOrder();//拷贝构造BSTree<int> t2 = t;t2.InOrder();//查找cout << t2.Find(1) << endl;cout << t2.Find(8) << endl;//赋值重载BSTree<int> t3;t3 = t;t3.InOrder();//删除t3.Erase(4);t3.InOrder();t3.Erase(5);t3.InOrder();t3.Erase(3);t3.InOrder();t3.Erase(7);t3.InOrder();
}int main()
{Test();return 0;
}
三、二叉搜索树的应用
3.1 K模型
K模型:K模型即只有key作为关键码,结构中只需要存储Key即可,关键码即为需要搜索到的值
比如:给一个单词word,判断该单词是否拼写正确,具体方式如下:
- 以词库中所有单词集合中的每个单词作为key,构建一棵二叉搜索树
- 在二叉搜索树中检索该单词是否存在,存在则拼写正确,不存在则拼写错误
3.2 KV模型
KV模型:每一个关键码 Key,都有与之对应的值 Value,即<Key, Value>的键值对,通过Key查找 Value
该种方式在现实生活中非常常见:
比如英汉词典就是英文与中文的对应关系,通过英文可以快速找到与其对应的中文,英文单词与其对应的中文<word, chinese>就构成一种键值对;
再比如统计单词次数,统计成功后,给定单词就可快速找到其出现的次数,单词与其出现次数就是<word, count>就构成一种键值对
四、二叉搜索树的性能分析
插入和删除操作都必须先查找,查找效率代表了二叉搜索树中各个操作的性能
对有n个结点的二叉搜索树,若每个元素查找的概率相等,则二叉搜索树平均查找长度是结点在二叉搜索树的深度的函数,即结点越深,则比较次数越多。但对于同一个关键码集合,如果各关键码插入的次序不同,可能得到不同结构的二叉搜索树
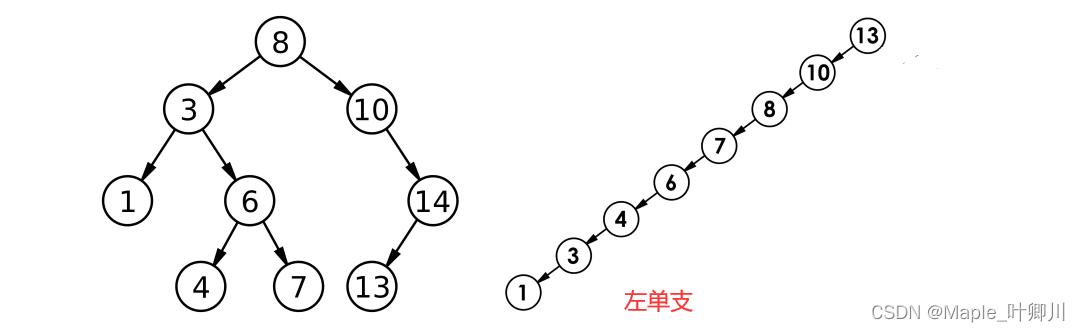
对于有n个结点的二叉搜索树:
- 最优的情况下,二叉搜索树为完全二叉树,其平均比较次数为:O(logN)
- 最差的情况下,二叉搜索树退化为单支树,其平均比较次数为:O(N / 2)
所以实际上,二叉搜索树在极端情况下是没办法保证效率的,因此由二叉搜索树又衍生出来了AVL树、红黑树,后面准备学
----------------我是分割线---------------
文章到这里就结束了,下一篇即将更新
相关文章:

【C++进阶】三、二叉搜索树
目录 一、二叉搜索树 1.1 概念 1.2 二叉搜索树操作 二、二叉搜索树实现 2.1 框架总览 2.2 实现接口总览 2.2.1 构造函数 2.2.2 拷贝构造 2.2.3 赋值重载 2.2.4 析构函数 2.2.5 二叉搜索树的遍历 2.2.6 插入函数 2.2.7 查找函数 2.2.8 删除函数 2.3 二叉搜索数完整…...

电脑系统崩溃怎么修复教程
系统崩溃了怎么办? 如今的软件是越来越复杂、越来越庞大。由系统本身造成的崩溃即使是最简单的操作,比如关闭系统或者是对BIOS进行升级都可能会对PC合操作系统造成一定的影响。下面一起来看看电脑系统崩溃修复方法步骤。 工具/原料: 系统版本…...

语义分割数据标注案例分析
语义分割(Semantic Segmentation)是计算机视觉领域中的一种重要任务,它的目的是将图像中的每个像素分配到对应的语义类别中。简单来说,就是将一张图像分割成多个区域,并为每个像素指定一个标签,标识出它属于…...

回归预测 | MATLAB实现GRU(门控循环单元)多输入单输出(多指标评价)
回归预测 | MATLAB实现GRU(门控循环单元)多输入单输出(多指标评价) 文章目录 回归预测 | MATLAB实现GRU(门控循环单元)多输入单输出(多指标评价)预测效果基本介绍程序设计参考资料预测效果 基本介绍 GRU神经网络是LST...
驱动程序开发:Buildroot根文件系统构建并加载驱动文件xxx.ko测试
目录一、buildroot根文件系统简介二、buildroot下载三、buildroot构建根文件系统1、配置 buildroot①配置 Target options②配置 Toolchain③配置 System configuration④配置 Filesystem images⑤禁止编译 Linux 内核和 uboot2、 buildroot 下的 busybox 配置①修改 Makefile&…...

R+VIC模型融合实践技术应用及未来气候变化模型预测
目录 理论专题一:VIC模型的原理及特点 综合案例一:基于QGIS的VIC模型建模 理论专题二:VIC模型率定验证 综合案例二:基于R语言VIC参数率定和优化 理论专题三:遥感技术与未来气候变化 综合案例三:运用V…...
第六章.决策树(Decision Tree)—ID3算法,C4.5算法
第六章.决策树(Decision Tree) 6.1 ID3算法,C4.5算法 1.决策树适用的数据类型 比较适合分析离散数据,如果是连续数据要先转换成离散数据再做分析 2.信息熵 1).概念: 一条信息的信息量大小和它的不确定性有直接的关系,要搞清楚一件非常不确…...
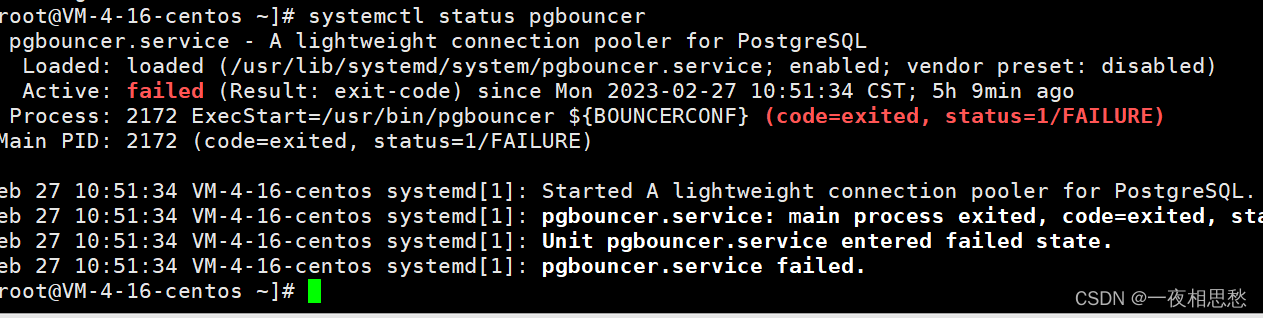
springboot+pgbouncer+postgres数据库连接池集成方案及问题解决
期望通过每一次分享,让技术的门槛变低,落地更容易。 —— around 前言 旨在解决微服务项目全是连接池并影响数据库并发连接,作者的环境是基于sprongboot微服务连接postgres数据库,每个微服务的DAO层配置都使用了连接池技术。后续…...

Mysql 常用日期处理函数
Mysql 常用日期处理函数 1 建表语句 SET NAMES utf8mb4; SET FOREIGN_KEY_CHECKS 0; -- ---------------------------- -- Table structure for emp -- ---------------------------- DROP TABLE IF EXISTS emp; CREATE TABLE emp (EMPNO int(4) NOT NULL,ENAME varchar(10…...

Pod中容器的健康检查
健康检查 上篇文章中我们了解了Pod中容器的生命周期的两个钩子函数,PostStart与PreStop,其中PostStart是在容器创建后立即执行的,而PreStop这个钩子函数则是在容器终止之前执行的。除了上面这两个钩子函数以外,还有一项配置会影响…...
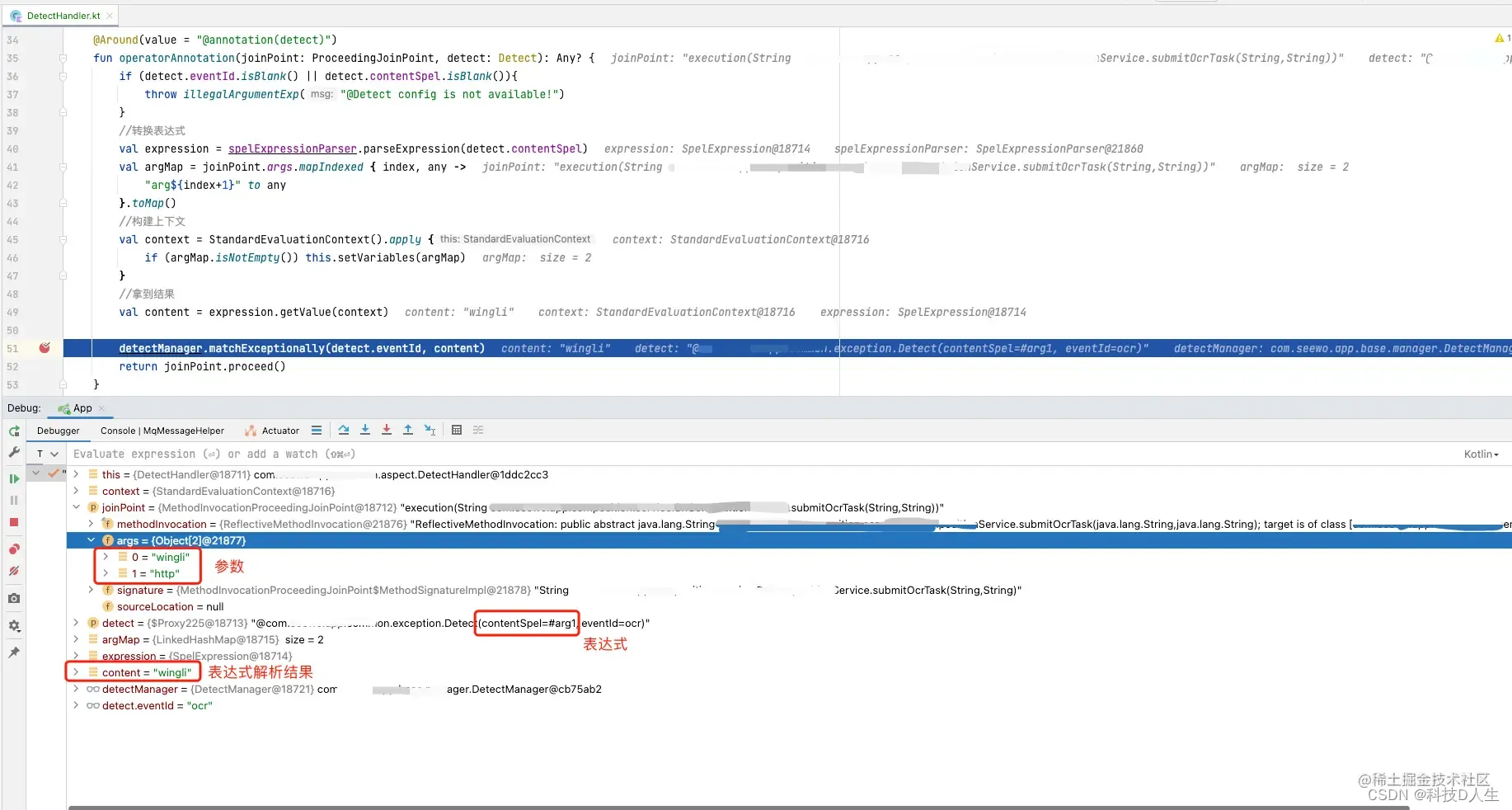
信贷系统学习总结(5)—— 简单的风控示例(含代码)
一、背景1.为什么要做风控?目前我们业务有使用到非常多的AI能力,如ocr识别、语音测评等,这些能力往往都比较费钱或者费资源,所以在产品层面也希望我们对用户的能力使用次数做一定的限制,因此风控是必须的!2.为什么要自己写风控?那么多开源的风控组件,为什么还要写呢?是不是想…...
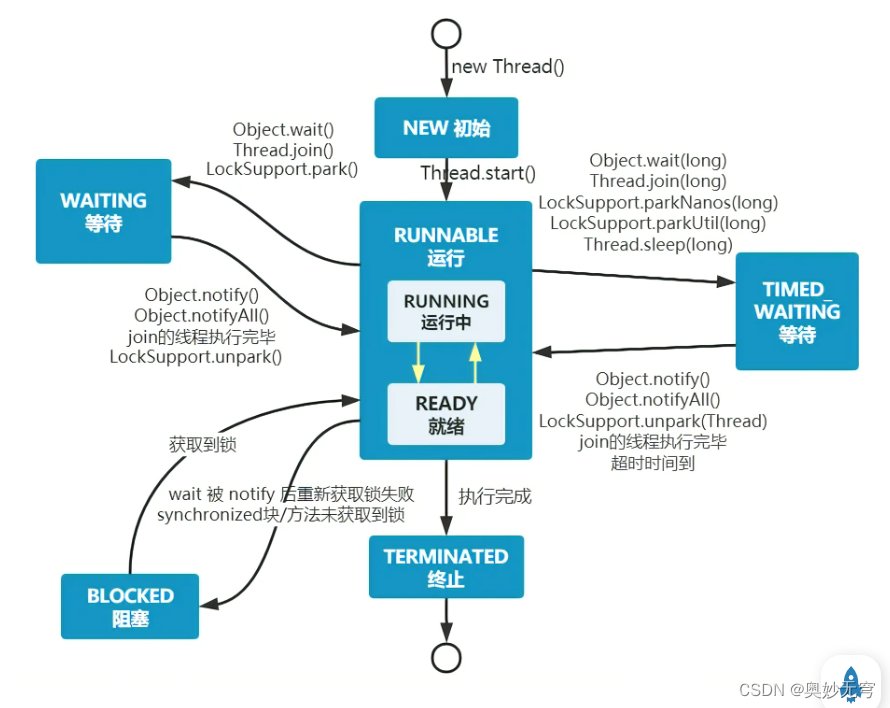
Java知识复习(四)多线程、并发编程
1、进程、线程和程序 进程:进程是程序的一次执行过程,是系统运行程序的基本单位,因此进程是动态的;在 Java 中,当我们启动 main 函数时其实就是启动了一个 JVM 的进程,而 main 函数所在的线程就是这个进程…...

一个9个月测试经验的人,居然在面试时跟我要18K,我都被他吓到了····
2月初我入职了深圳某家创业公司,刚入职还是很兴奋的,到公司一看我傻了,公司除了我一个测试,公司的开发人员就只有3个前端2个后端还有2个UI,在粗略了解公司的业务后才发现是一个从零开始的项目,目前啥都没有…...
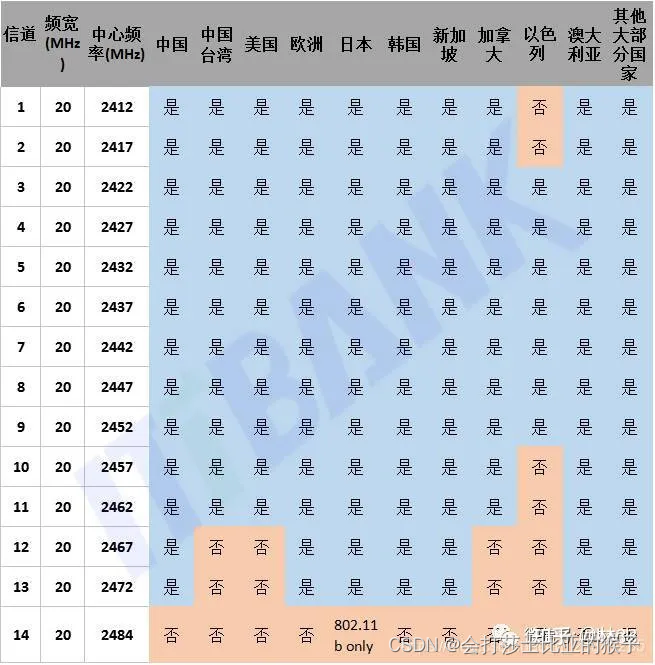
zigbee与WIFI同频干扰问题
zigbee与WIFI同频干扰 为了降低Wifi信道与Zigbee信道的同频干扰问题,Zigbee联盟在《Zigbee Home Automation Public Application Profile》中推荐使用11,14,15,19,20,24,25这七个信道。 为什么呢,我们看一下Wifi和Zigbee的信道分布。 WiFi带宽对干扰的…...
git拉取指定的单个或多个文件或文件夹
直接上步骤 初始化仓库 git init拉取远程仓库信息,省略号为仓库地址 git remote add -f origin http://****.git开启 sparse clone git config core.sparsecheckout true配置需要拉取的文件夹 有一个指定一个,有多个指定多个,路径写对即可&a…...
不是,到底有多少种图片懒加载方式?
一、也是我最开始了解到的 js方法,利用滚动事件,判断当时的图片位置是否在可视框内,然后进行渲染。 弊端:代码冗杂,你还要去监听页面的滚动事件,这本身就是一个不建议监听的事件,即便是我们做了…...

CAD坐标有哪些输入方式?来看看这些CAD坐标输入方式!
在CAD设计过程中,有时需要通过已知坐标点来画图,有时又需要通过已知角度和距离来画图,在这种情况下,由于已知条件不同,所以便需要用不同的方式来定位点。那么,你知道CAD坐标有哪些输入方式吗?本…...
铰链、弹簧,特殊的物理关节
title: 铰链、弹簧,特殊的物理关节 date: 2023-02-28T13:32:57Z lastmod: 2023-02-28T14:24:06Z 铰链关节(Hinge Join)组件 组件-Physics-Hinge Join Anchor 当物体挂载铰链组件以后,组件下Anchor等同于边长为1的立方体。当这…...

Android Studio相关记录
目录Android Studio 便捷插件Android LogcatJava文件的类头模板Android Studio 使用遇到的问题解决方案org.jetbrains.annotations.NullableBuild 控制台编译输出中文乱码Terminal 使用 git 命令窗口git 命令窗口中文乱码Android Studio 便捷插件 Android Logcat 配置路径 Fi…...
Linux 基础介绍-基础命令
文章目录01 学习目标02 Linux/Unix 操作系统简介2.1 Linux 操作系统的目标2.2 Linux 操作系统的作用2.3 Unix 家族历史2.4 Linux 家族历史2.5 Linux 和Unix 的联系2.6 Linux 内核介绍2.7 Linux 发行版本2.8 Unix/Linux 开发应用领域介绍03 Linux 目录结构3.1 Win 和Linux 文件系…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

leetcode_69.x的平方根
题目如下 : 看到题 ,我们最原始的想法就是暴力解决: for(long long i 0;i<INT_MAX;i){if(i*ix){return i;}else if((i*i>x)&&((i-1)*(i-1)<x)){return i-1;}}我们直接开始遍历,我们是整数的平方根,所以我们分两…...
动态规划-1035.不相交的线-力扣(LeetCode)
一、题目解析 光看题目要求和例图,感觉这题好麻烦,直线不能相交啊,每个数字只属于一条连线啊等等,但我们结合题目所给的信息和例图的内容,这不就是最长公共子序列吗?,我们把最长公共子序列连线起…...

基于stm32F10x 系列微控制器的智能电子琴(附完整项目源码、详细接线及讲解视频)
注:文章末尾网盘链接中自取成品使用演示视频、项目源码、项目文档 所用硬件:STM32F103C8T6、无源蜂鸣器、44矩阵键盘、flash存储模块、OLED显示屏、RGB三色灯、面包板、杜邦线、usb转ttl串口 stm32f103c8t6 面包板 …...

计算机系统结构复习-名词解释2
1.定向:在某条指令产生计算结果之前,其他指令并不真正立即需要该计算结果,如果能够将该计算结果从其产生的地方直接送到其他指令中需要它的地方,那么就可以避免停顿。 2.多级存储层次:由若干个采用不同实现技术的存储…...
数据挖掘是什么?数据挖掘技术有哪些?
目录 一、数据挖掘是什么 二、常见的数据挖掘技术 1. 关联规则挖掘 2. 分类算法 3. 聚类分析 4. 回归分析 三、数据挖掘的应用领域 1. 商业领域 2. 医疗领域 3. 金融领域 4. 其他领域 四、数据挖掘面临的挑战和未来趋势 1. 面临的挑战 2. 未来趋势 五、总结 数据…...
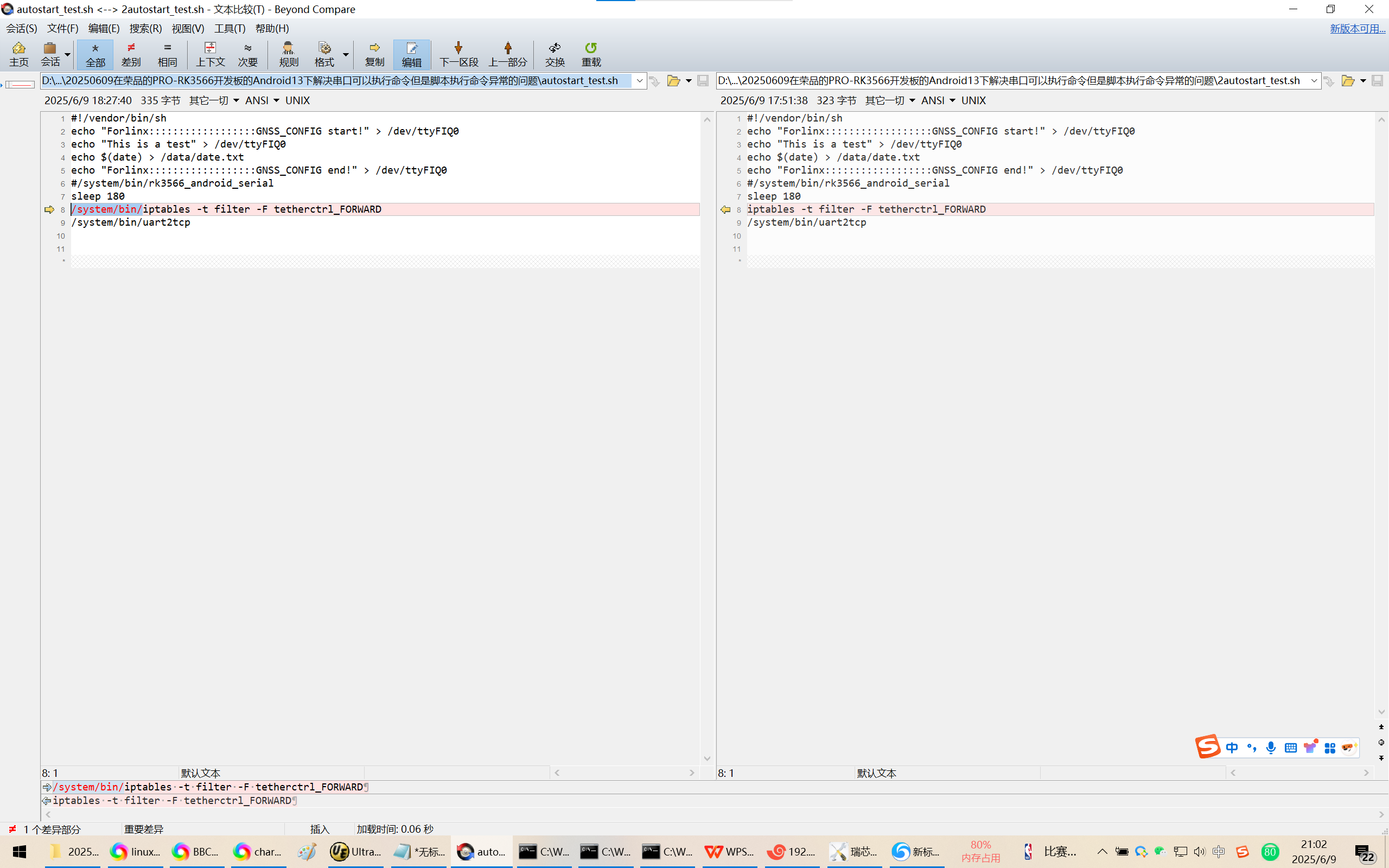
20250609在荣品的PRO-RK3566开发板的Android13下解决串口可以执行命令但是脚本执行命令异常的问题
20250609在荣品的PRO-RK3566开发板的Android13下解决串口可以执行命令但是脚本执行命令异常的问题 2025/6/9 20:54 缘起,为了跨网段推流,千辛万苦配置好了网络参数。 但是命令iptables -t filter -F tetherctrl_FORWARD可以在调试串口/DEBUG口正确执行。…...

使用VMware克隆功能快速搭建集群
自己搭建的虚拟机,后续不管是学习java还是大数据,都需要集群,java需要分布式的微服务,大数据Hadoop的计算集群,如果从头开始搭建虚拟机会比较费时费力,这里分享一下如何使用克隆功能快速搭建一个集群 先把…...
