第六章.决策树(Decision Tree)—ID3算法,C4.5算法
第六章.决策树(Decision Tree)
6.1 ID3算法,C4.5算法
1.决策树适用的数据类型
比较适合分析离散数据,如果是连续数据要先转换成离散数据再做分析
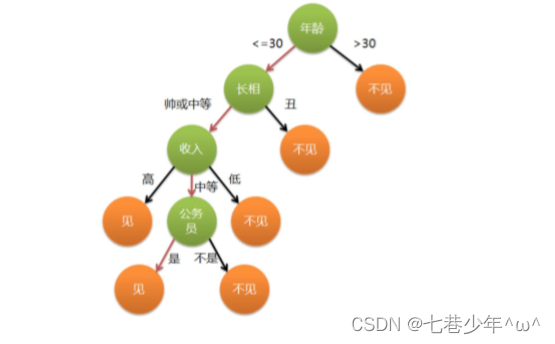
2.信息熵
1).概念:
- 一条信息的信息量大小和它的不确定性有直接的关系,要搞清楚一件非常不确定的事情(或者是我们一无所知的事情),需要了解大量信息->信息量的度量就等于不确定性的多少
2).公式:
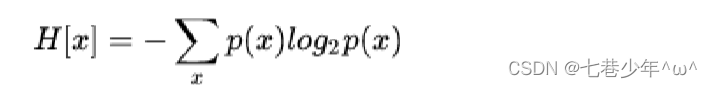
3).示例:
-
示例1:
假设有一个普通骰子A,扔出1-6的概率都是1/6;骰子B,扔出1-5的概率为10%,扔出6的概率为50%,骰子C,扔出6的概率为100% -
计算:
①.骰子A:

②.骰子B:
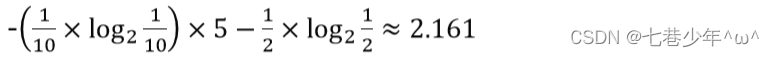
③.骰子C:

3.ID3算法
决策树会选择最大化信息增益来对结点进行划分。
1).信息增益计算公式:
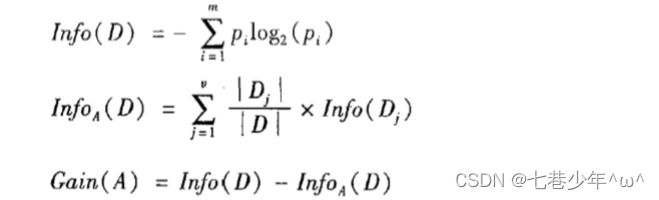
2).公式示例:
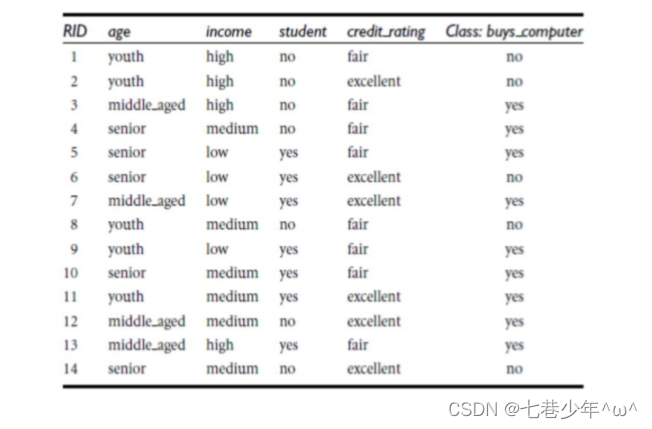
- 分析:
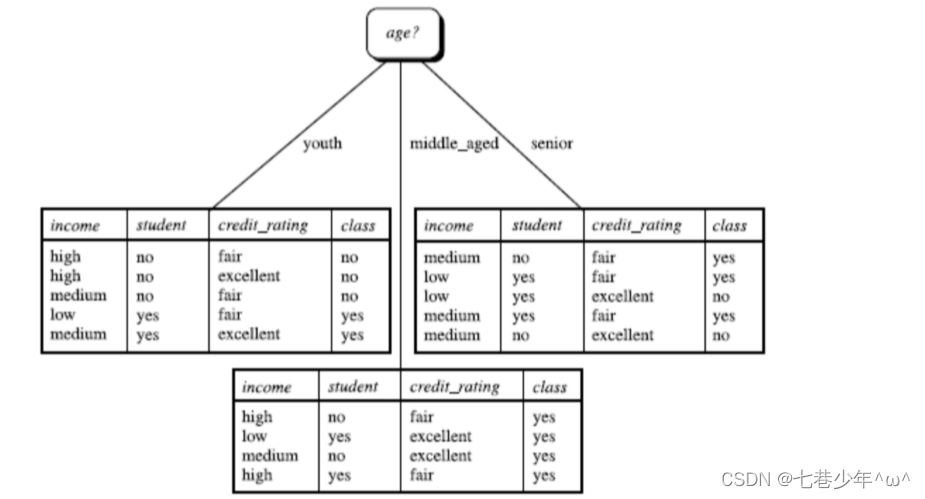
- 计算:

说明:
①.9/14,5/14对应Class:buys_computer那一列。
3).ID3算法示例:
·AllElectronics.csv中的数据:
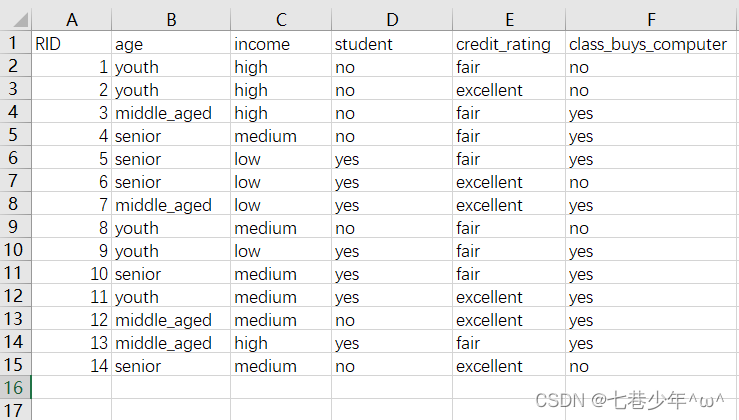
·代码:
from sklearn.feature_extraction import DictVectorizer
from sklearn import tree
from sklearn import preprocessing
import graphviz
import csv# 导入数据
DTree = open(r'D:\\data\\AllElectronics.csv', 'r')
reader = csv.reader(DTree)#使用import csv是因为表格中含有很多字符# 获取第一行数据
headers = reader.__next__()
# print(headers)# 定义两个列表
featureList = []
labelList = []for row in reader:# 把Label存入ListlabelList.append(row[-1])rowDict = {}for i in range(1, len(row) - 1):# 建立一个数据字典rowDict[headers[i]] = row[i]featureList.append(rowDict)# print(featureList)# 把数据转换成01表示
vec = DictVectorizer()
x_data = vec.fit_transform(featureList).toarray()
# print('x_data:'+ str(x_data))# 打印属性名称
feature_names = vec.get_feature_names_out()
# print(feature_names)# 打印标签
# print('labelList:'+ str(labelList))# 把标签转换成01表示
lb = preprocessing.LabelBinarizer()
y_data = lb.fit_transform(labelList)
# print('y_data'+str(y_data))# 创建并拟合模型
DTree_model = tree.DecisionTreeClassifier(criterion='entropy')
DTree_model.fit(x_data, y_data)# 测试
x_test = x_data[0]
print('x_test:' + str(x_test))predictions = DTree_model.predict(x_test.reshape(1, -1))#变成二维数据
print('predict:' + str(predictions))# 导出决策树
dot_data = tree.export_graphviz(DTree_model, out_file=None, feature_names=feature_names, class_names=lb.classes_,filled=True, rounded=True, special_characters=True)graph = graphviz.Source(dot_data)
graph.render('computer')·结果展示: (文件会保存在运行目录下)
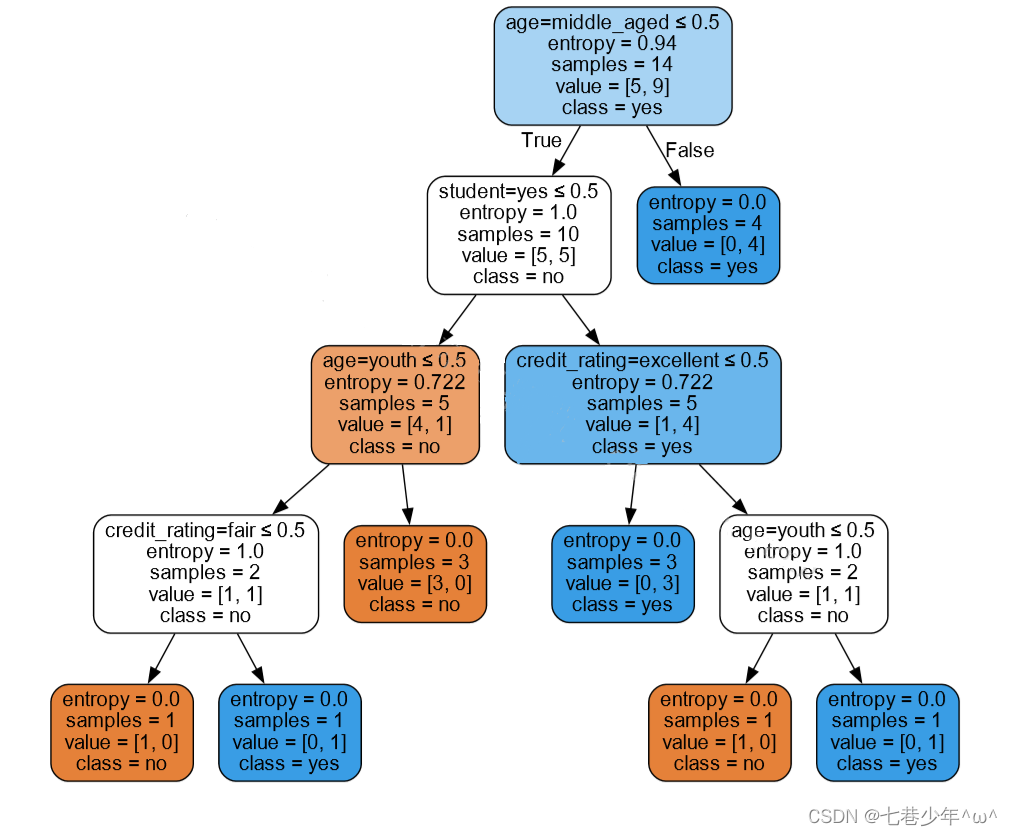
4.C4.5算法
ID3算法存在的缺陷:信息增益的方法倾向于首先选择因子数较多的变量。C4.5算法是ID3算法的优化版本。
1).信息增益的改进-增益率:
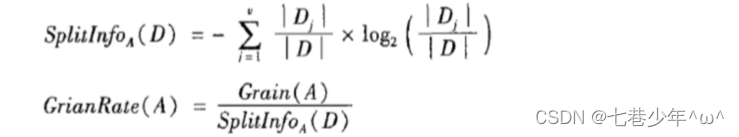
相关文章:
第六章.决策树(Decision Tree)—ID3算法,C4.5算法
第六章.决策树(Decision Tree) 6.1 ID3算法,C4.5算法 1.决策树适用的数据类型 比较适合分析离散数据,如果是连续数据要先转换成离散数据再做分析 2.信息熵 1).概念: 一条信息的信息量大小和它的不确定性有直接的关系,要搞清楚一件非常不确…...
springboot+pgbouncer+postgres数据库连接池集成方案及问题解决
期望通过每一次分享,让技术的门槛变低,落地更容易。 —— around 前言 旨在解决微服务项目全是连接池并影响数据库并发连接,作者的环境是基于sprongboot微服务连接postgres数据库,每个微服务的DAO层配置都使用了连接池技术。后续…...

Mysql 常用日期处理函数
Mysql 常用日期处理函数 1 建表语句 SET NAMES utf8mb4; SET FOREIGN_KEY_CHECKS 0; -- ---------------------------- -- Table structure for emp -- ---------------------------- DROP TABLE IF EXISTS emp; CREATE TABLE emp (EMPNO int(4) NOT NULL,ENAME varchar(10…...

Pod中容器的健康检查
健康检查 上篇文章中我们了解了Pod中容器的生命周期的两个钩子函数,PostStart与PreStop,其中PostStart是在容器创建后立即执行的,而PreStop这个钩子函数则是在容器终止之前执行的。除了上面这两个钩子函数以外,还有一项配置会影响…...
信贷系统学习总结(5)—— 简单的风控示例(含代码)
一、背景1.为什么要做风控?目前我们业务有使用到非常多的AI能力,如ocr识别、语音测评等,这些能力往往都比较费钱或者费资源,所以在产品层面也希望我们对用户的能力使用次数做一定的限制,因此风控是必须的!2.为什么要自己写风控?那么多开源的风控组件,为什么还要写呢?是不是想…...
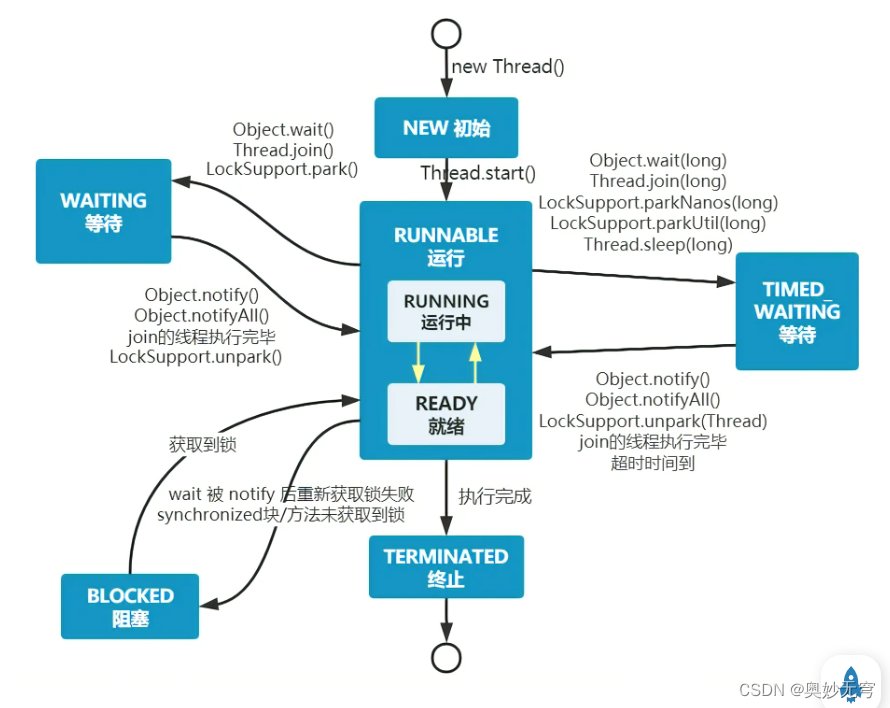
Java知识复习(四)多线程、并发编程
1、进程、线程和程序 进程:进程是程序的一次执行过程,是系统运行程序的基本单位,因此进程是动态的;在 Java 中,当我们启动 main 函数时其实就是启动了一个 JVM 的进程,而 main 函数所在的线程就是这个进程…...

一个9个月测试经验的人,居然在面试时跟我要18K,我都被他吓到了····
2月初我入职了深圳某家创业公司,刚入职还是很兴奋的,到公司一看我傻了,公司除了我一个测试,公司的开发人员就只有3个前端2个后端还有2个UI,在粗略了解公司的业务后才发现是一个从零开始的项目,目前啥都没有…...
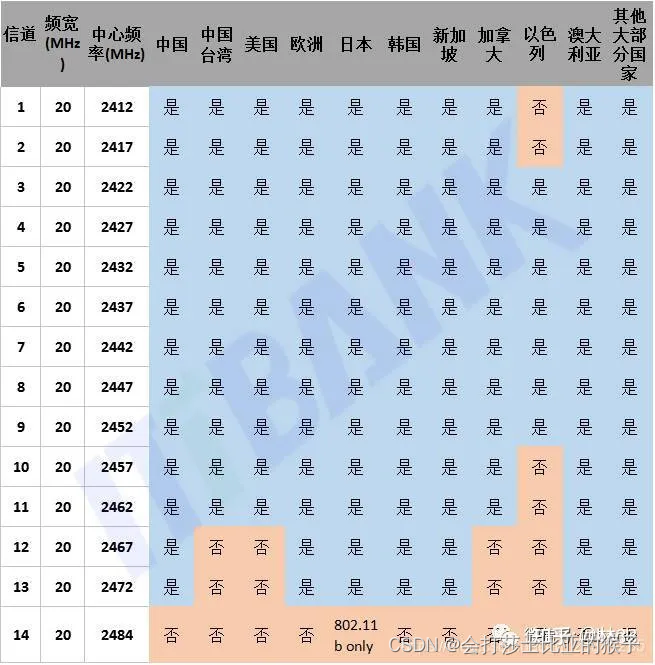
zigbee与WIFI同频干扰问题
zigbee与WIFI同频干扰 为了降低Wifi信道与Zigbee信道的同频干扰问题,Zigbee联盟在《Zigbee Home Automation Public Application Profile》中推荐使用11,14,15,19,20,24,25这七个信道。 为什么呢,我们看一下Wifi和Zigbee的信道分布。 WiFi带宽对干扰的…...
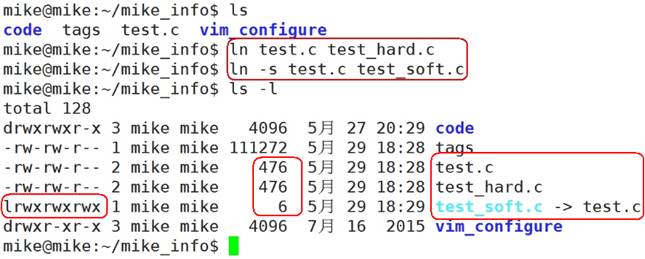
git拉取指定的单个或多个文件或文件夹
直接上步骤 初始化仓库 git init拉取远程仓库信息,省略号为仓库地址 git remote add -f origin http://****.git开启 sparse clone git config core.sparsecheckout true配置需要拉取的文件夹 有一个指定一个,有多个指定多个,路径写对即可&a…...
不是,到底有多少种图片懒加载方式?
一、也是我最开始了解到的 js方法,利用滚动事件,判断当时的图片位置是否在可视框内,然后进行渲染。 弊端:代码冗杂,你还要去监听页面的滚动事件,这本身就是一个不建议监听的事件,即便是我们做了…...

CAD坐标有哪些输入方式?来看看这些CAD坐标输入方式!
在CAD设计过程中,有时需要通过已知坐标点来画图,有时又需要通过已知角度和距离来画图,在这种情况下,由于已知条件不同,所以便需要用不同的方式来定位点。那么,你知道CAD坐标有哪些输入方式吗?本…...
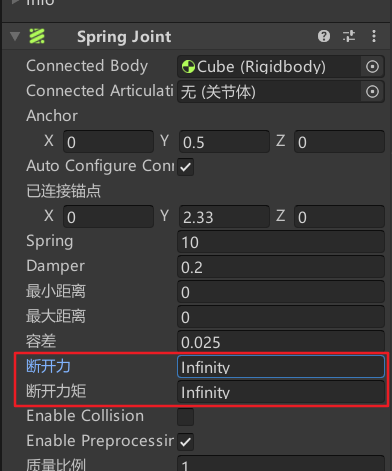
铰链、弹簧,特殊的物理关节
title: 铰链、弹簧,特殊的物理关节 date: 2023-02-28T13:32:57Z lastmod: 2023-02-28T14:24:06Z 铰链关节(Hinge Join)组件 组件-Physics-Hinge Join Anchor 当物体挂载铰链组件以后,组件下Anchor等同于边长为1的立方体。当这…...

Android Studio相关记录
目录Android Studio 便捷插件Android LogcatJava文件的类头模板Android Studio 使用遇到的问题解决方案org.jetbrains.annotations.NullableBuild 控制台编译输出中文乱码Terminal 使用 git 命令窗口git 命令窗口中文乱码Android Studio 便捷插件 Android Logcat 配置路径 Fi…...
Linux 基础介绍-基础命令
文章目录01 学习目标02 Linux/Unix 操作系统简介2.1 Linux 操作系统的目标2.2 Linux 操作系统的作用2.3 Unix 家族历史2.4 Linux 家族历史2.5 Linux 和Unix 的联系2.6 Linux 内核介绍2.7 Linux 发行版本2.8 Unix/Linux 开发应用领域介绍03 Linux 目录结构3.1 Win 和Linux 文件系…...

Linux 进程:程序地址空间 与 虚拟内存
目录一、程序地址空间二、虚拟地址空间1.虚拟内存的原理2.使用虚拟内存的原因?3.如何实现虚拟空间?4.使用虚拟内存的好处本文主要介绍程序地址空间和虚拟地址空间的概念,理解了虚拟地址空间,才可以更好的理解物理内存和进程pcb之间…...

python 密码学编程
最近在看一本书。名字是 python密码学编程。在此做一些笔记,同时也为有需要的人提供一些参考。 ******************************************************************** * quote : "http://inventwithpython.com/" …...

【C++ | bug | 运算符重载】定义矩阵(模板)类时,使用 “友元函数” 进行 * 运算符重载时编译报错
作者:非妃是公主 专栏:《C》 博客地址:https://blog.csdn.net/myf_666 个性签:顺境不惰,逆境不馁,以心制境,万事可成。——曾国藩 文章目录专栏推荐一、类的声明及函数定义二、错误信息三、问题…...
)
数学小课堂:无穷小(以动态的眼光看待世界,理解无限的世界)
文章目录 引言I 芝诺四个著名的悖论1.1 二分法悖论:从A点到B点是不可能的。1.2 阿喀琉斯悖论:阿喀琉斯追不上乌龟。1.3 飞箭不动悖论:射出去的箭是静止的。1.4 基本空间和相对运动悖论II 回答芝诺的悖论2.1 阿喀琉斯悖论2.2 相对运动悖论III 无穷小3.1 无穷小的定义3.1 无穷…...
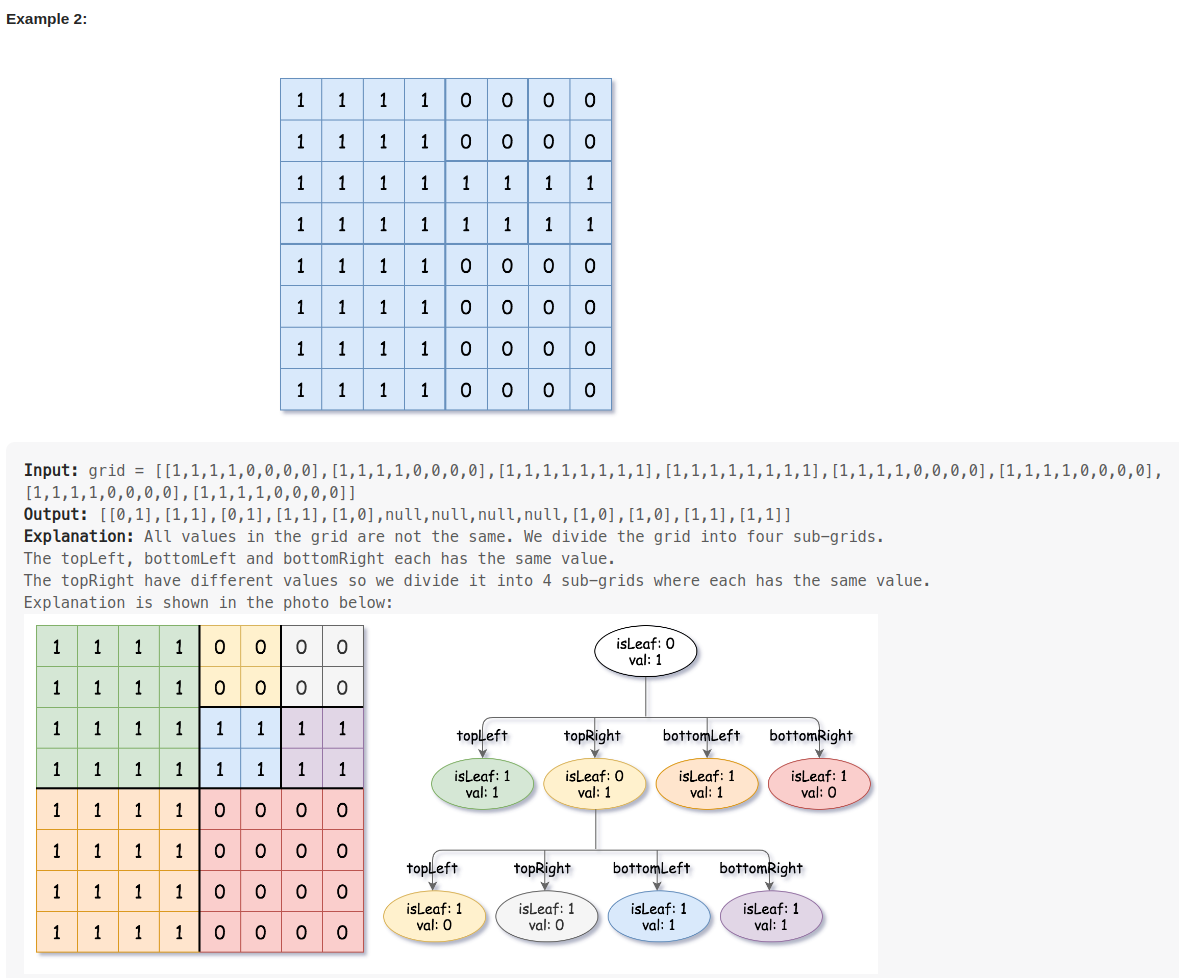
leetcode 427. Construct Quad Tree(构建四叉树)
刚看到题的时候是懵的,这也太长了。到底是要表达什么呢。 不妨把这个矩阵看成一个正方形的图片,想象你在处理图片,从整体逐步到局部。 刚开始看一整张图片,如果是全0或全1,这个就是叶子节点,怎么表达叶子节…...
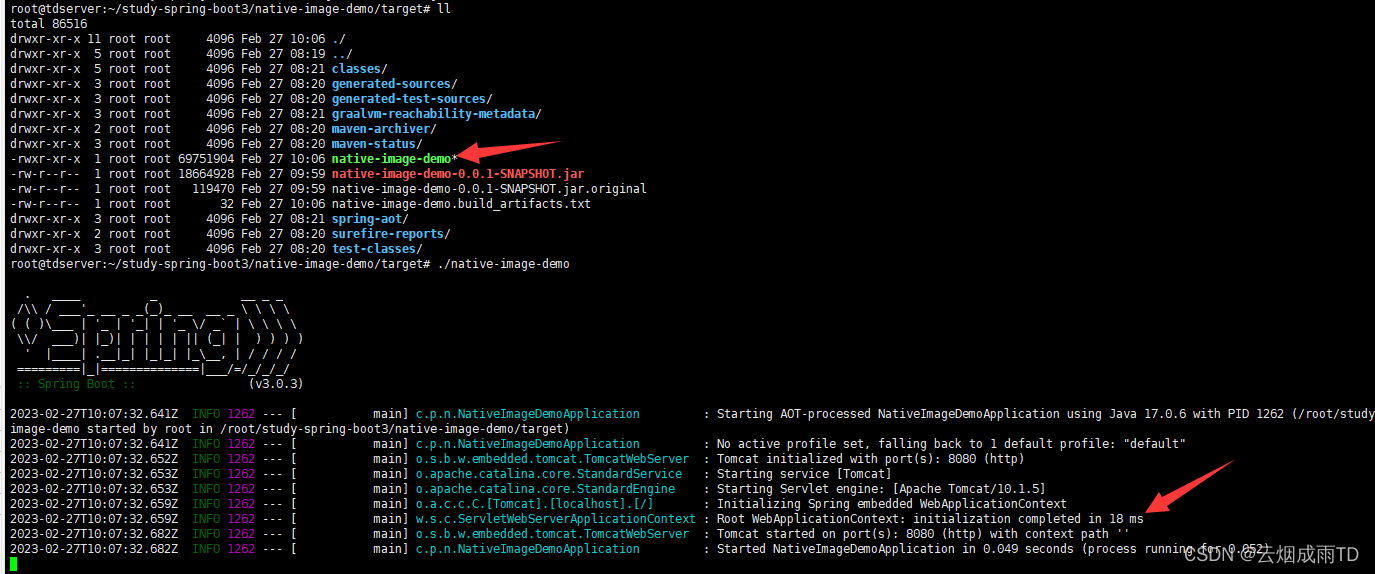
Spring Boot 3.0系列【2】部署篇之使用GraalVM构建原生镜像
有道无术,术尚可求,有术无道,止于术。 本系列Spring Boot版本2.7.0 文章目录概述JIT & AOTJIT (动态编译)AOT(静态编译)GraalVM简介运行模式Native Image(原生镜像)…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...
