离散数学笔记_第一章:逻辑和证明(2 )
1.2 命题逻辑的应用
- 1.2.1 语句翻译
- 1.2.2 系统规范说明
- 1.2.3 布尔搜索
- 1.2.4 逻辑谜题
- 泥巴孩子谜题
- 骑士和流氓
- (考研逻辑题)
- 1.
- 1.2.5 逻辑电路
1.2.1 语句翻译
🐳为啥要翻译语句?
➡因语言常常有二义性(有歧义,尤其是博大精深的汉语),把语句翻译成复合命题可以消除歧义!
把语句翻译成逻辑表达式的过程:
step①:设原子命题变量
step②:用所设的这些变量,通过逻辑联结词,表示出语句的各个部分
step③:把各个部分再通过逻辑联结词组合成最终的复合命题
1.2.2 系统规范说明
描述硬件系统和软件系统的时候,将自然语言语句翻译成逻辑表达式是很重要的一部分。系统和软件工程师根据自然语言描述的需求,生成精确而无二义的规范说明。
注意:系统规范说明应该是一致的!!!
⭐⭐⭐"一致"指的是: 存在同时为真的情况。
1.2.3 布尔搜索
逻辑联结词广泛用于海量信息如网页索引的搜索中。由于搜索采用命题逻辑的技术,因此被称为布尔搜索
布尔搜索中,联结词AND用于匹配同时包含两个搜索项的记录;OR用于匹配两个搜索项之一或者两项均匹配的记录;NOT(有时写作AND NOT),用于排除某个特定搜索项👇

1.2.4 逻辑谜题
泥巴孩子谜题
父亲让两个孩子(一个男孩和一个女孩)在后院玩耍,并让他们不要把身上搞脏。然而,在玩耍的过程中,两个孩子额头上都沾了泥。当孩子们回来后,父亲说:"你们当中至少有一个人额头上有泥。“然后要求孩子们用"是"和"否"回答问题:“你知道你额头上是否有泥吗?“父亲问了两遍同样的问题。假设每个孩子都可以看到对方的额头上是否有泥,但不能看见自己的额头,孩子们在每次被问到这个问题时将会怎样回答呢?(假设两个孩子都很诚实并且都同时回答每一次提问)
解:令 s 和 d 分别表示语句"儿子的额头上有泥"和"女儿的额头上有泥”。当父亲说:“你们当中至少有一个人额头上有泥"时,表示的是 sVd 为真。当父亲第一次问那个问题时两个孩子都将回答"否”,因为他们都看到对方的额头上有泥。也就是说,儿子知道 d 为真,但不知道 s 是否为真。而女儿知道 s 为真,但不知道 d 是否为真。
在儿子对第一次询问回答"否"后,女儿可以判断出 d 必为真。这是因为问第一次问题时,儿子知道 sVd 为真,但不能判断 s 是否为真。利用这个信息,女儿能够得出结论 d 必定为真,因为如果 d 为假,则儿子就有理由推出,由于 sVd 为真,那么 s 必定为真,因此他对第一个问题的回答应为"是”。儿子也可以类似推断出 s 必为真。因此,第二次两个孩子都将回答"是”。
骑士和流氓
一个岛上居住着两类人——骑士和流氓。骑士说的都是真话,而流氓总是说谎。现在碰到了两个人A和B,如果A说“B是骑士”,B说“我们两人不是一类人”。请判断A、B两人到底是骑士还是流氓。
解:每个人要么是骑士,要么是流氓。给出假设通过判断是否产生矛盾,来求解。
假设A是骑士(说真话),则B也是骑士,那么B也应当说真话,但B所说的与A说的矛盾→A不是骑士。
假设A是流氓(说假话),则B也是流氓,那么B也应当说谎话,可以判断出AB不矛盾,所以A和B都是流氓。
(考研逻辑题)
1.
某项测试共有4道题,每道题给出A、B、C、D四个选项,其中只有一项是正确答案。现有张、王、赵、李4人参加了测试,他们的答题情况和测试结果如下:
答题者第一题第二题第三题第四题测试结果:
①张A B A B均不正确
②王B D B C只答对一题
③赵D A A B均不正确
④李C C B D只答对一题
I、根据以上信息,可以得出以下哪项?
A.第二题的正确答案是C
B.第二题的正确答案是D
C.第三题的正确答案是D
D.第四题的正确答案是C
E.第四题的正确答案是A
II、如果每道题的正确答案各不相同,则可以得出以下哪项?
A.第一题的正确答案是B
B.第一题的正确答案是C
C.第二题的正确答案是D
D.第二题的正确答案是A
E.第三题的正确答案是C
解:由①、③得:
 B D B C只答对一题
B D B C只答对一题
C C B D只答对一题
Ⅰ假设第一题B对,则第二题的D、第三题的B、第四题的C错。
再根据CCBD只对一题,得:

Ⅱ假设第二题D对,则第一题的B、第三题的B、第四题的C错。再根据CCBD只对一题,得:
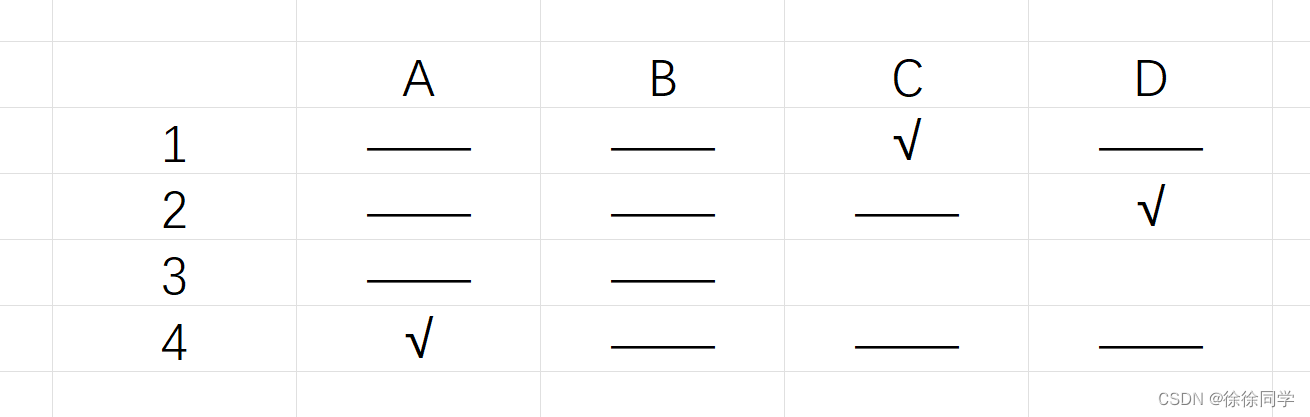 Ⅲ假设第三题B对,第一题的B、第二题的D、第四题的C错。
Ⅲ假设第三题B对,第一题的B、第二题的D、第四题的C错。
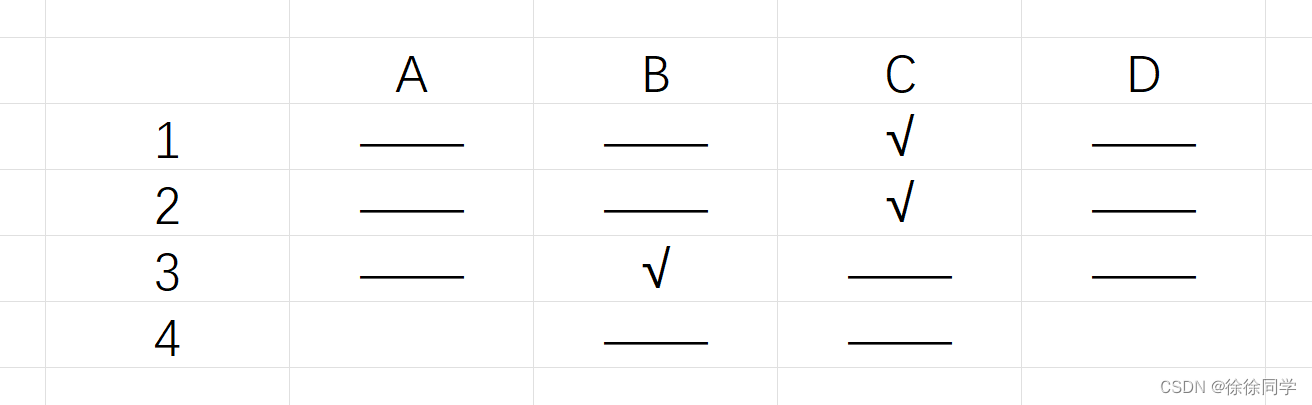 与C C B D只答对一题矛盾,故第三题B错
与C C B D只答对一题矛盾,故第三题B错
Ⅳ假设第四题C对,则第一题的B、第二题的D、第三题的B错。
 与C C B D只答对一题矛盾,故第四题C错
与C C B D只答对一题矛盾,故第四题C错
最终可以得到:

答案I.E、II.A
1.2.5 逻辑电路
逻辑电路(又叫做数字电路)接受输入信号p1,p2,······,pn,每个信号1bit[或0(关)或1(开)],产生输出信号s1,s2,······,sn, 每个1bit.
一般来说,数字电路可以有多个输出,但在这一节中只讨论只有一个输出信号的数字电路。
复杂的数字电路可以从三种基本的门电路构造而来:
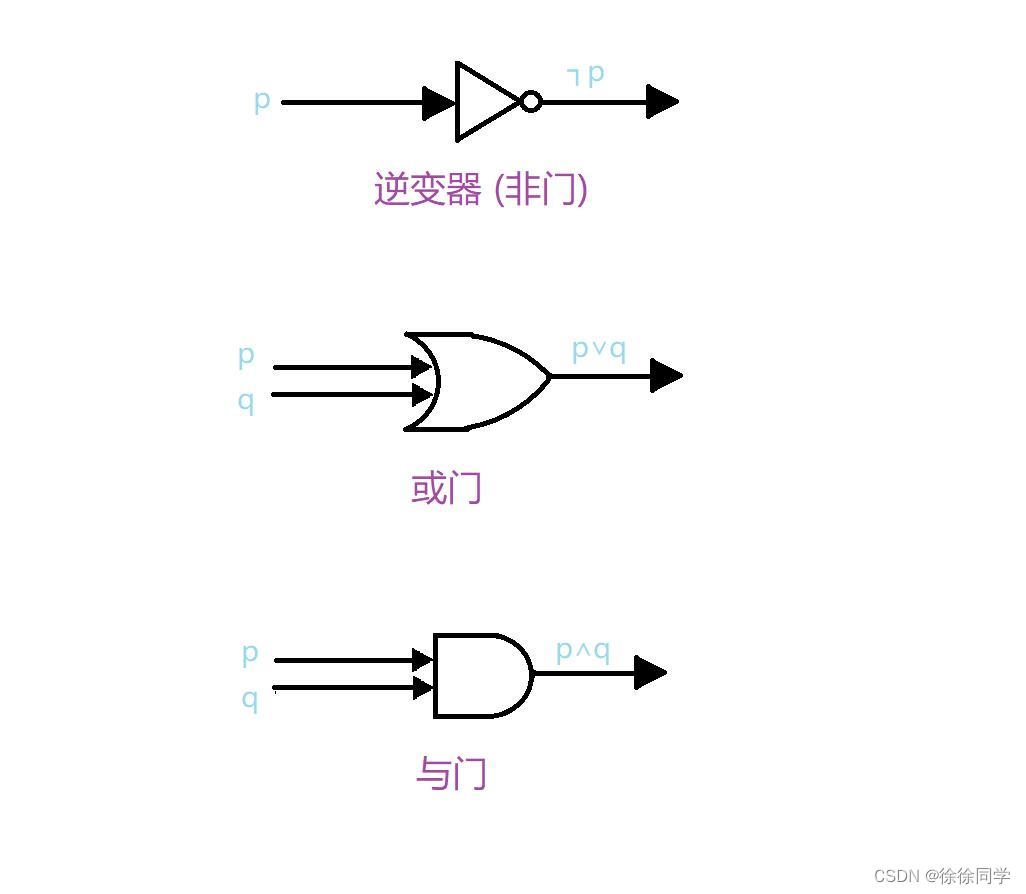
(网上没找着,自己在画图里画的,有些粗糙,见谅~)
相关文章:

离散数学笔记_第一章:逻辑和证明(2 )
1.2 命题逻辑的应用1.2.1 语句翻译 1.2.2 系统规范说明 1.2.3 布尔搜索 1.2.4 逻辑谜题泥巴孩子谜题骑士和流氓(考研逻辑题)1.1.2.5 逻辑电路1.2.1 语句翻译 🐳为啥要翻译语句? ➡因语言常常有二义性(有歧义&#x…...

MFCC语音特征值提取算法
博主简介 博主是一名大二学生,主攻人工智能研究。感谢让我们在CSDN相遇,博主致力于在这里分享关于人工智能,c,Python,爬虫等方面知识的分享。 如果有需要的小伙伴可以关注博主,博主会继续更新的,…...

TencentOS3.1编译安装redis6.2.5
下载地址:https://redis.io/download 最近版为7.0.8,本次安装的是6.2.5 软件包解包并进入目录。 redis是c语言编写的,编译需要gcc,按网上资料说默认安装的gcc版本过低(可能是4.8.5),使用rpm …...

AI顶会accepted papers list
为方便相关paper调研,对相关顶会文章列表和下载地址汇总,会议包括:AAAI、ACL、IJCAI、ICLR、COLING、SIGIR、WSDM、WWW、ICML、KDD、NeurIPS、CVPR、ECCV、ACM MM 2023 Accepted papers list 更新于:(2022.11.24&…...
IOS逆向之frida安装
首先手机要越狱,这个就不说了,博主就是咸鱼搞了个160的苹果6, 自己刷到苹果6支持最新的12.5.7版本后越狱; 谁让他低版本,不支持 CrackerXI砸壳呢,当时你要是使用 frida-ios-dump 也是可以的; …...

《金山区提信心扩需求稳增长促发展行动方案》的通知
金发改规〔2023〕1号 各镇政府、街道办事处、园区管委会,区政府各部门、各直属单位: 《金山区提信心扩需求稳增长促发展行动方案》已经区委、区政府同意,现印发给你们,请认真按照执行。 附件:金山区提信心扩需求稳增…...
【Redis】Java客户端JedisSpringDataRedis入门(三)
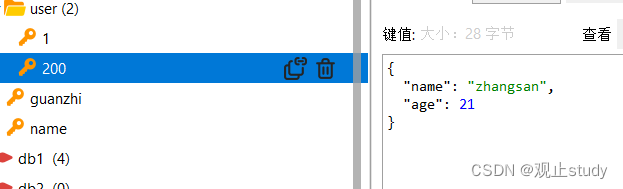
🚗Redis学习第三站~ 🚩起始站:【Redis】概述&环境搭建(一) 🚩本文已收录至专栏:数据库学习之旅 👍希望您能有所收获 在上一篇中我们学习了Redis常见命令的使用,显然,我们不可能一…...

挑选销售自动化工具应该关注什么功能?
销售自动化可以极大地提高你的生产力和效率,每周都为你节省时间。这样,你就可以把更多的时间用于完成交易,而减少用于行政任务的时间。市面上的销售自动化工具有很多,作为一般经验法则,以下是销售自动化工具中需要寻找…...
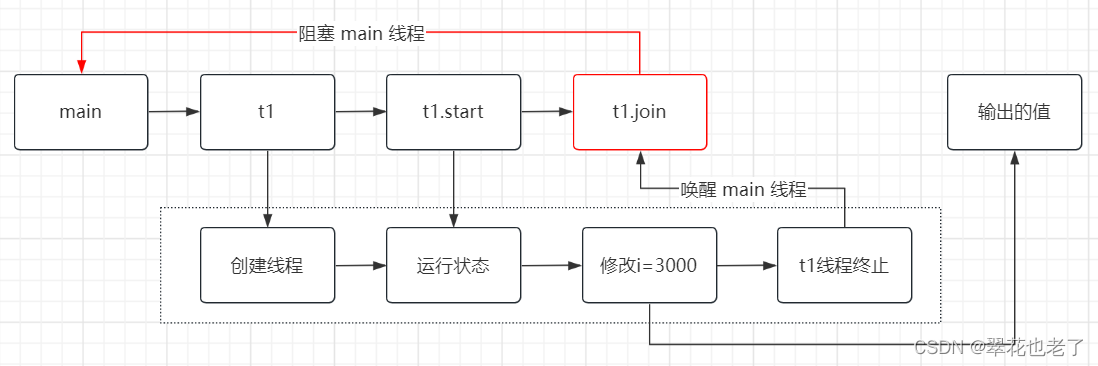
thread.join 是干什么的?原理是什么?
Thread.join 加了join,表示join的线程的修改对于join之外的代码是可见的。 代码示例: public class JoinDemo {private static int i 1000;public static void main(String[] args) {new Thread(()->{i 3000;}).start();System.out.println("…...

论文阅读 | Cross-Attention Transformer for Video Interpolation
前言:ACCV2022wrokshop用transformer做插帧的文章,q,kv,来自不同的图像 代码:【here】 Cross-Attention Transformer for Video Interpolation 引言 传统的插帧方法多用光流,但是光流的局限性在于 第一&…...
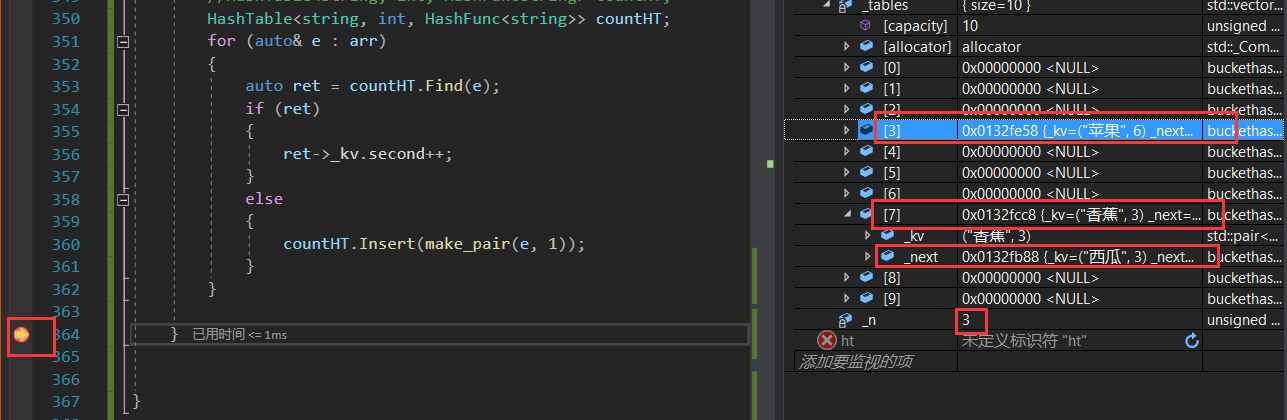
【C++修炼之路】22.哈希
每一个不曾起舞的日子都是对生命的辜负 哈希一.哈希概念及性质1.1 哈希概念1.2 哈希冲突1.3 哈希函数二.哈希冲突解决2.1 闭散列/开放定址法2.2 开散列/哈希桶三.开放定址法代码3.1 插入Insert3.2 查找Find3.3 删除Erase3.4 映射的改良&完整代码四.开散列代码4.1 插入Inser…...
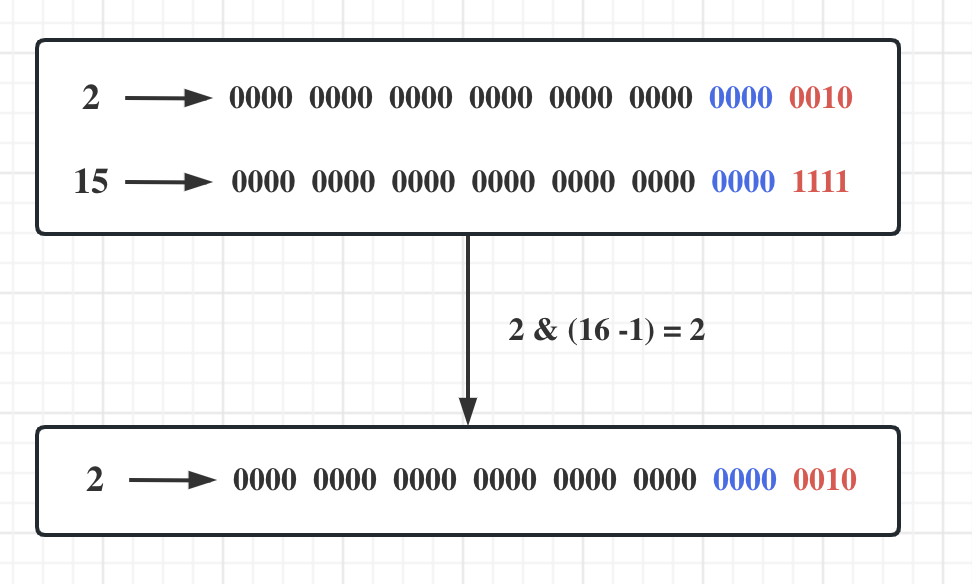
HashMap原理(一):哈希函数的设计
目录导航哈希函数的作用与本质哈希函数设计哈希表初始容量的校正哈希表容量为2的整数次幂的缺陷及解决办法注:为了简化代码,提高语义,本文将HashMap很多核心代码抽出并根据代码含义为代码片段取名,完全是为了方便读者理解。哈希函…...
06--WXS 脚本
1、简介WXS(WeiXin Script)是小程序的一套脚本语言,结合 WXML ,可以构建出页面的结构。 注意事项WXS 不依赖于运行时的基础库版本,可以在所有版本的小程序中运行。WXS 与 JavaScript 是不同的语言,有自己的…...
【Vue3】vue3 + ts 封装城市选择组件
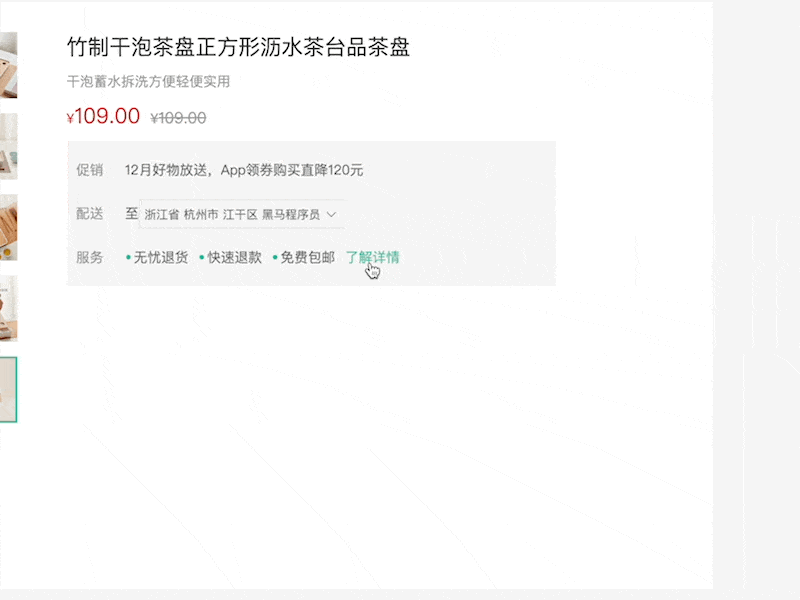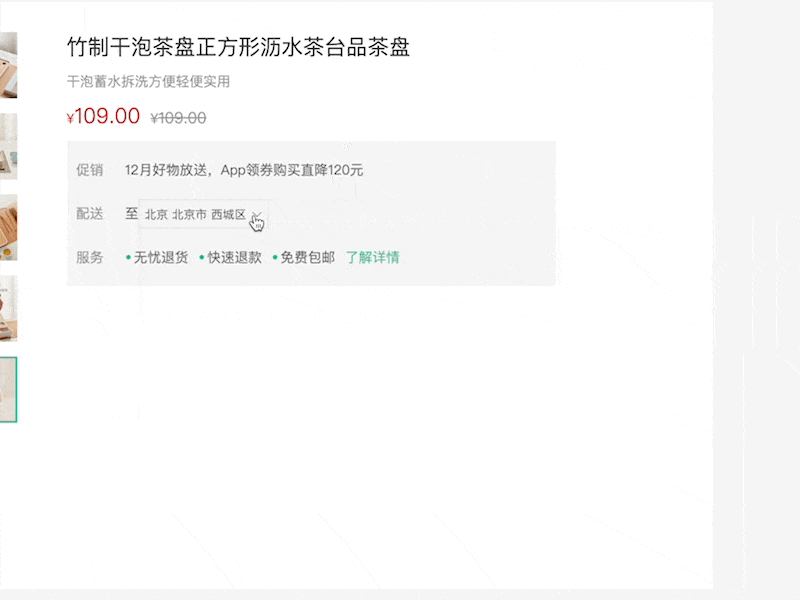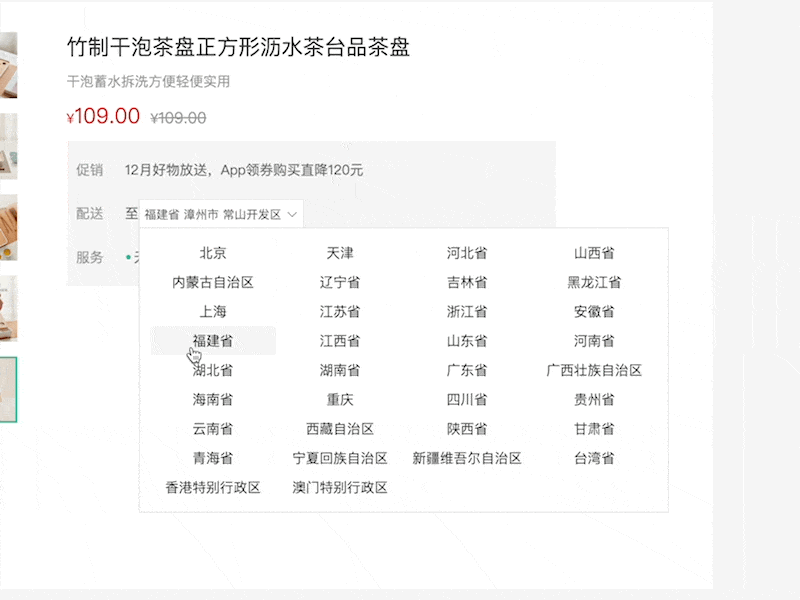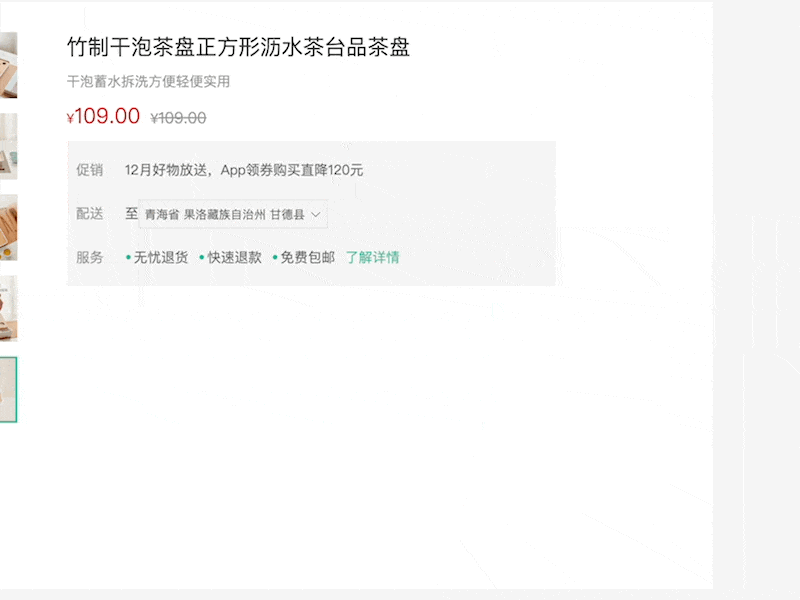
城市选择-基本功能 能够封装城市选择组件,并且完成基础的显示隐藏的交互功能 (1)封装通用组件src/components/city/index.vue <script lang"ts" setup name"City"></script> <template><div class…...
C语言if判断语句的三种用法
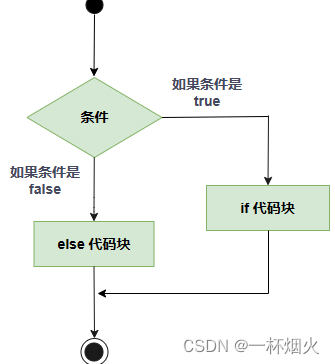
C if 语句 一个 if 语句 由一个布尔表达式后跟一个或多个语句组成。 语法 C 语言中 if 语句的语法: if(boolean_expression) {/* 如果布尔表达式为真将执行的语句 */ }如果布尔表达式为 true,则 if 语句内的代码块将被执行。如果布尔表达式为 false&…...

React中echarts的封装
做大屏的时候经常会遇到 echarts 展示 在 React (^18.2.0) 中对 echarts (^5.4.0) 的简单封装 echarts 封装使用 props 说明 参数说明类型可选值默认值opts初始化传入的 opts https://echarts.apache.org/zh/api.html#echarts…...

IV测试系统3A太阳能模拟器在光伏中应用
一、概述IV测试系统3A太阳能模拟器应具备光束准直、光斑均匀、辐照稳定、且与太阳光谱匹配的特点,使用户可足不出户的完成需要太阳光照条件的测试。科迎法电气提供多规格高品质的太阳模拟器,可适用于单晶硅、多晶硅、非晶硅、染料敏化、有机、钙钛矿等各…...
Vue 中过滤器 filter 使用教程
Vue 过滤器 filter 使用教程文章目录Vue 过滤器 filter 使用教程一、过滤器1.1 过滤器使用的背景1.2 格式化时间的不同实现1.3 过滤器的使用1.4 过滤器总结一、过滤器 1.1 过滤器使用的背景 过滤器提供给我们的一种数据处理方式。过滤器功能不是必须要使用的,因为它…...
源码numpy笔记
参考文章 numpy学习 numpy中的浅复制和深复制的详细用法 numpy中的np.where torch.gather() Numpy的核心数据结构,就叫做array就是数组,array对象可以是一维数组,也可以是多维数组 array本身的属性 shape:返回一个元组…...
【VUE】六 路由和传值
目录 一、 路由和传值 二、案例 三、案例存在无法刷新问题 一、 路由和传值 当某个组件可以根据某些参数值的不同,展示不同效果时,需要用到动态路由。 例如:访问网站看到课程列表,点击某个课程,就可以跳转到课程详…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...
