机器学习笔记之流形模型——标准流模型基本介绍

引言

本节将介绍概率生成模型——标准流模型($\text{Normalizing Flow}$)。

回顾：隐变量模型的缺陷

关于隐变量模型($\text{Latent Variable Model,LVM}$)，如果表示隐变量的随机变量集合$\mathcal{Z}$足够复杂的话，很容易出现积分难问题：
此时隐变量$\mathcal{Z}$的维度(随机变量个数)极高$(\mathcal{M})$,对$\mathcal{Z}$求解积分的代价是极大的$(\text{Intractable})$.
$$\begin{array}{rl}\underset{\text{Intractable}}{\underbrace{\mathcal{P}(\mathcal{X})}}& ={\int }_{\mathcal{Z}}\mathcal{P}(\mathcal{Z},\mathcal{X})d\mathcal{Z}\\ & ={\int }_{\mathcal{Z}}\mathcal{P}(\mathcal{Z})\cdot \mathcal{P}(\mathcal{X}\mid \mathcal{Z})d\mathcal{Z}\\ & ={\int }_{{\mathcal{Z}}_1}\cdots {\int }_{{\mathcal{Z}}_{\mathcal{M}}}\mathcal{P}({\mathcal{Z}}_1,\cdots ,{\mathcal{Z}}_{\mathcal{M}})\cdot \mathcal{P}(\mathcal{X}\mid {\mathcal{Z}}_1,\cdots ,{\mathcal{Z}}_{\mathcal{M}})d{\mathcal{Z}}_1,\cdots ,{\mathcal{Z}}_{\mathcal{M}}\end{array}$$
从而，关于隐变量$\mathcal{Z}$的后验概率$\mathcal{P}(\mathcal{Z}\mid \mathcal{X})$也同样是极难求解的：
$$\begin{array}{rl}\underset{\text{Intractable}}{\underbrace{\mathcal{P}(\mathcal{Z}\mid \mathcal{X})}}& =\frac{\mathcal{P}(\mathcal{Z},\mathcal{X})}{\mathcal{P}(\mathcal{X})}\\ & =\frac{\mathcal{P}(\mathcal{Z})\cdot \mathcal{P}(\mathcal{X}\mid \mathcal{Z})}{\underset{\text{Intractable}}{\underbrace{\mathcal{P}(\mathcal{X})}}}\end{array}$$

针对这种问题，由于无法得到精确解/精确解计算代价极高，因而通常采用近似推断($\text{Approximate Inference}$)的方式对$\mathcal{P}(\mathcal{Z}\mid \mathcal{X})$近似求解。

例如变分自编码器($\text{Variational Auto-Encoder,VAE}$)，它的底层逻辑是使用重参数化技巧将人为设定分布$\mathcal{Q}(\mathcal{Z}\mid \mathcal{X})$视作关于参数$\varphi$的函数$\mathcal{Q}(\mathcal{Z}\mid \mathcal{X},\varphi )$，并通过神经网络学习参数$\varphi$并使其近似$\mathcal{P}(\mathcal{Z}\mid \mathcal{X})$。关于变分自编码器的模型结构表示如下：

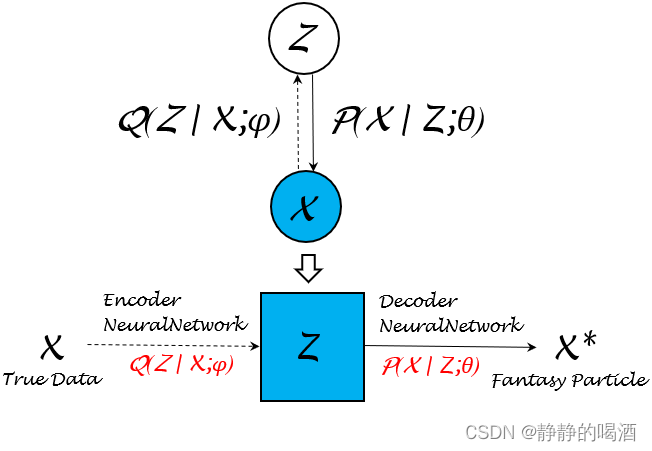
关于编码器($\text{Encoder}$)函数$\mathcal{Q}(\mathcal{Z}\mid \mathcal{X};\varphi )$与解码器($\text{Decoder}$)函数$\mathcal{P}(\mathcal{X}\mid \mathcal{Z};\theta )$，变分自编码器的目标函数表示如下：
一个有趣的现象：其中$-\text{KL}[\mathcal{Q}(\mathcal{Z}\mid \mathcal{X};\varphi )||\mathcal{P}(\mathcal{Z};{\theta }^{(t)})]$只是一个关于$\varphi$的惩罚项(约束)，并且这个约束直接作用于${\mathbb{E}}_{\mathcal{Q}(\mathcal{Z}\mid \mathcal{X};\varphi )}\left[\log \mathcal{P}(\mathcal{X}\mid \mathcal{Z};\theta )\right]$.因此真正迭代的只有参数$\theta ({\theta }^{(t)}\Rightarrow {\theta }^{(t+1)})$,参数$\varphi$仅是迭代过程中伴随着$\theta$的更新而更新。
$$\{\begin{array}{l}\mathcal{L}(\varphi ,\theta ,{\theta }^{(t)})={\mathbb{E}}_{\mathcal{Q}(\mathcal{Z}\mid \mathcal{X};\varphi )}\left[\log \mathcal{P}(\mathcal{X}\mid \mathcal{Z};\theta )\right]-\text{KL}[\mathcal{Q}(\mathcal{Z}\mid \mathcal{X};\varphi )||\mathcal{P}(\mathcal{Z};{\theta }^{(t)})]\\ \\ ({\hat{\theta }}^{(t+1)},{\hat{\varphi }}^{(t+1)})=\underset{\theta ,\varphi }{\mathrm{argmax}}\mathcal{L}(\varphi ,\theta ,{\theta }^{(t)})\end{array}$$
关于目标函数$\mathcal{L}(\varphi ,\theta ,{\theta }^{(t)})$的底层逻辑是最大化$\text{ELBO}$：
$$({\hat{\theta }}^{(t+1)},{\hat{\varphi }}^{(t+1)})=\underset{\theta ,\varphi }{\mathrm{argmax}}\left\{{\mathbb{E}}_{\mathcal{Q}(\mathcal{Z}\mid \mathcal{X};\varphi )}\left[\log \frac{\mathcal{P}(\mathcal{X},\mathcal{Z};\theta )}{\mathcal{Q}(\mathcal{Z}\mid \mathcal{X};\varphi )}\right]\right\}$$
也就是说，它仅仅是最大化了极大似然估计$\log \mathcal{P}(\mathcal{X};\theta )$的下界。实际上，它并没有直接对对数似然函数求解最优化问题。

这不可避免地存在误差，毕竟最优化对数似然函数和最优化它的下界 是两个概念。这一切的核心问题均在于$\mathcal{P}(\mathcal{X})$无法得到精确解。

如果存在一种模型，它在学习任务过程中，$\mathcal{P}(\mathcal{X})$是可求解的($\text{tractable}$)，自然不会出现上述一系列的近似操作了。

标准流($\text{Normalizing Flow}$)思想

关于样本$\mathcal{X}$的概率分布$\mathcal{P}(\mathcal{X})$，它可能是复杂的。但流模型($\text{Flow-based Model}$)的思想是：分布$\mathcal{P}(\mathcal{X})$的复杂并不是一蹴而就的，而是通过若干次的变化而产生出的复杂结果。

关于流模型的概率图结构可表示为如下形式：

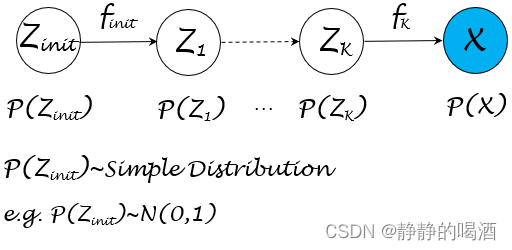
从模型结构中可以观察到，既然分布$\mathcal{P}(\mathcal{X})$比较复杂，那么可以构建隐变量$\mathcal{Z}$与$\mathcal{X}$之间的函数关系$\mathcal{X}=f(\mathcal{Z})$，从而通过换元的方式描述$\mathcal{P}(\mathcal{Z})$与$\mathcal{P}(\mathcal{X})$的函数关系。

如果隐变量$\mathcal{Z}$的结构同样复杂，可以继续针对该隐变量创造新的隐变量并构建函数关系。以此类推，最终可以通过一组服从简单分布的随机变量${\mathcal{Z}}_{init}$通过若干次的函数的嵌套表示，得到关于$\mathcal{X}$的关联关系，从而得到${\mathcal{P}}_{init}({\mathcal{Z}}_{init})\Rightarrow \mathcal{P}(\mathcal{X})$的函数关系。

分布变换的推导过程

以上图中隐变量${\mathcal{Z}}_{\mathcal{K}}$和观测变量$\mathcal{X}$之间关联关系示例：

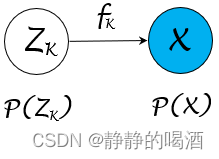
• 创建假设：$f_{\mathcal{K}}$是一个 连续、可逆 函数，满足$\mathcal{X}=f_{\mathcal{K}}({\mathcal{Z}}_{\mathcal{K}})$。其中${\mathcal{Z}}_{\mathcal{K}},\mathcal{X}$均表示随机变量集合，并服从对应的概率分布：
  • 其中${\mathcal{P}}_{\mathcal{X}}(\mathcal{X})$表示关于$\mathcal{X}$的概率分布，并且变量是$\mathcal{X}.{\mathcal{Z}}_{\mathcal{K}}$对应分布同理。
  • 反过来，由于$f_{\mathcal{K}}$函数可逆，因而有：${\mathcal{Z}}_{\mathcal{K}}=f_{\mathcal{K}}^{-1}(\mathcal{X})$.
    $${\mathcal{Z}}_{\mathcal{K}}\sim {\mathcal{P}}_{{\mathcal{Z}}_{\mathcal{K}}}({\mathcal{Z}}_{\mathcal{K}}),\mathcal{X}\sim {\mathcal{P}}_{\mathcal{X}}(\mathcal{X});{\mathcal{Z}}_{\mathcal{K}},\mathcal{X}\in {\mathbb{R}}^p$$
• 不可否认的是，无论是${\mathcal{P}}_{{\mathcal{Z}}_{\mathcal{K}}}({\mathcal{Z}}_{\mathcal{K}})$还是${\mathcal{P}}_{\mathcal{X}}(\mathcal{X})$，它们都是概率分布。根据概率密度积分的定义，必然有：
  $${\int }_{{\mathcal{Z}}_{\mathcal{K}}}{\mathcal{P}}_{{\mathcal{Z}}_{\mathcal{K}}}({\mathcal{Z}}_{\mathcal{K}})d{\mathcal{Z}}_{\mathcal{K}}={\int }_{\mathcal{X}}{\mathcal{P}}_{\mathcal{X}}(\mathcal{X})d\mathcal{X}=1$$
  从而有：
  在变分推断——重参数化技巧一节中也使用这种描述进行换元,在不定积分中,${\mathcal{P}}_{{\mathcal{Z}}_{\mathcal{K}}}({\mathcal{Z}}_{\mathcal{K}})d{\mathcal{Z}}_{\mathcal{K}}$和${\mathcal{P}}_{\mathcal{X}}(\mathcal{X})d\mathcal{X}$必然相等;但是在定积分中,${\mathcal{Z}}_{\mathcal{K}},\mathcal{X}$位于不同的特征空间，对应的积分值(有正有负)存在差异。因此需要加上‘模’符号。
  $$|{\mathcal{P}}_{{\mathcal{Z}}_{\mathcal{K}}}({\mathcal{Z}}_{\mathcal{K}})d{\mathcal{Z}}_{\mathcal{K}}|=|P_{\mathcal{X}}(\mathcal{X})d\mathcal{X}|$$
  但由于${\mathcal{P}}_{{\mathcal{Z}}_{\mathcal{K}}}({\mathcal{Z}}_{\mathcal{K}}),{\mathcal{P}}_{\mathcal{X}}(\mathcal{X})$它们是概率密度函数，它们的实际结果表示概率值(恒正)。因此$|{\mathcal{P}}_{\mathcal{X}}(\mathcal{X})|={\mathcal{P}}_{\mathcal{X}}(\mathcal{X})$，${\mathcal{P}}_{{\mathcal{Z}}_{\mathcal{K}}}({\mathcal{Z}}_{\mathcal{K}})$同理。经过移项，可将概率分布之间的关系表示为如下形式：
  $${\mathcal{P}}_{\mathcal{X}}(\mathcal{X})=\left|\frac{d{\mathcal{Z}}_{\mathcal{K}}}{d\mathcal{X}}\right|\cdot {\mathcal{P}}_{{\mathcal{Z}}_{\mathcal{K}}}({\mathcal{Z}}_{\mathcal{K}})$$
  将${\mathcal{Z}}_{\mathcal{K}}=f_{\mathcal{K}}^{-1}(\mathcal{X})$代入，最终可得到如下形式：
  $${\mathcal{P}}_{\mathcal{X}}(\mathcal{X})=\left|\frac{\partial f_{\mathcal{K}}^{-1}(\mathcal{X})}{\partial \mathcal{X}}\right|\cdot {\mathcal{P}}_{{\mathcal{Z}}_{\mathcal{K}}}({\mathcal{Z}}_{\mathcal{K}})$$
• 观察系数项$\left|\frac{\partial f_{\mathcal{K}}^{-1}(\mathcal{X})}{\partial \mathcal{X}}\right|$，它是一个标量、常数，但$\frac{\partial f_{\mathcal{K}}^{-1}(\mathcal{X})}{\partial \mathcal{X}}$自身是一个矩阵：
  该矩阵被称作雅可比矩阵$\text{Jacobian}$
  $$\frac{\partial f_{\mathcal{K}}^{-1}(\mathcal{X})}{\partial \mathcal{X}}={\left[\begin{array}{cccc}\frac{\partial f_{\mathcal{K}}^{-1}({\mathcal{X}}_1)}{\partial {\mathcal{X}}_1}& \frac{\partial f_{\mathcal{K}}^{-1}({\mathcal{X}}_1)}{\partial {\mathcal{X}}_2}& \cdots & \frac{\partial f_{\mathcal{K}}^{-1}({\mathcal{X}}_1)}{\partial {\mathcal{X}}_p}\\ \frac{\partial f_{\mathcal{K}}^{-1}({\mathcal{X}}_2)}{\partial {\mathcal{X}}_1}& \frac{\partial f_{\mathcal{K}}^{-1}({\mathcal{X}}_2)}{\partial {\mathcal{X}}_2}& \cdots & \frac{\partial f_{\mathcal{K}}^{-1}({\mathcal{X}}_2)}{\partial {\mathcal{X}}_p}\\ ⋮& ⋮& \ddots & ⋮\\ \frac{\partial f_{\mathcal{K}}^{-1}({\mathcal{X}}_p)}{\partial {\mathcal{X}}_1}& \frac{\partial f_{\mathcal{K}}^{-1}({\mathcal{X}}_p)}{\partial {\mathcal{X}}_2}& \cdots & \frac{\partial f_{\mathcal{K}}^{-1}({\mathcal{X}}_p)}{\partial {\mathcal{X}}_p}\end{array}\right]}_{p\times p}$$
  那么$\left|\frac{\partial f_{\mathcal{K}}^{-1}(\mathcal{X})}{\partial \mathcal{X}}\right|$实际上是与雅克比矩阵对应的雅克比行列式($\text{Jacobian Determinant}$)的绝对值。使用$\text{det}\left[\frac{\partial f_{\mathcal{K}}^{-1}(\mathcal{X})}{\partial \mathcal{X}}\right]$进行表示：
  $${\mathcal{P}}_{\mathcal{X}}(\mathcal{X})=\left|\text{det}\left[\frac{\partial f_{\mathcal{K}}^{-1}(\mathcal{X})}{\partial \mathcal{X}}\right]\right|\cdot {\mathcal{P}}_{{\mathcal{Z}}_{\mathcal{K}}}({\mathcal{Z}}_{\mathcal{K}})$$
• 继续变换，观察$\frac{\partial f_{\mathcal{K}}^{-1}(\mathcal{X})}{\partial \mathcal{X}}$，可以继续向下变换：
  $$\{\begin{array}{l}\frac{\partial f_{\mathcal{K}}^{-1}(\mathcal{X})}{\partial \mathcal{X}}\cdot \frac{\partial f_{\mathcal{K}}({\mathcal{Z}}_{\mathcal{K}})}{\partial {\mathcal{Z}}_{\mathcal{K}}}=1\Rightarrow \frac{\partial f_{\mathcal{K}}^{-1}(\mathcal{X})}{\partial \mathcal{X}}={\left[\frac{\partial f_{\mathcal{K}}({\mathcal{Z}}_{\mathcal{K}})}{\partial {\mathcal{Z}}_{\mathcal{K}}}\right]}^{-1}\\ \Rightarrow \left|\text{det}\left[\frac{\partial f_{\mathcal{K}}^{-1}(\mathcal{X})}{\partial \mathcal{X}}\right]\right|={\left|\text{det}\left[\frac{\partial f_{\mathcal{K}}({\mathcal{Z}}_{\mathcal{K}})}{\partial {\mathcal{Z}}_{\mathcal{K}}}\right]\right|}^{-1}\end{array}$$
  最终，分布${\mathcal{P}}_{\mathcal{X}}(\mathcal{X})$与分布${\mathcal{P}}_{{\mathcal{Z}}_{\mathcal{K}}}({\mathcal{Z}}_{\mathcal{K}})$之间的关系表示为：
  $${\mathcal{P}}_{\mathcal{X}}(\mathcal{X})={\left|\text{det}\left[\frac{\partial f_{\mathcal{K}}({\mathcal{Z}}_{\mathcal{K}})}{\partial {\mathcal{Z}}_{\mathcal{K}}}\right]\right|}^{-1}\cdot {\mathcal{P}}_{{\mathcal{Z}}_{\mathcal{K}}}({\mathcal{Z}}_{\mathcal{K}})$$

至此，从随机变量${\mathcal{Z}}_{\mathcal{K}}$与随机变量$\mathcal{X}$之间的函数关系，转化为概率分布${\mathcal{P}}_{\mathcal{X}}(\mathcal{X})$与${\mathcal{P}}_{{\mathcal{Z}}_{\mathcal{K}}}({\mathcal{Z}}_{\mathcal{K}})$之间的函数关系已表示出来。而流模型中的每一个过程均是基于上述关系，一层一层计算过来。

不同于以往对$\mathcal{P}(\mathcal{X})$的求解过程，它能够将$\mathcal{P}(\mathcal{X})$描述出来，直到使用隐变量的层数选择完成，其对应的$\mathcal{P}(\mathcal{X})$计算精度达到条件即可。关于流模型的学习方式依然是极大似然估计($\text{Maximum Likelihood Estimation,MLE}$)：
$$\begin{array}{rl}\log {\mathcal{P}}_{\mathcal{X}}(\mathcal{X})& =\log \left\{\prod _{k=1}^{\mathcal{K}}{\left|\text{det}\left[\frac{\partial f_k({\mathcal{Z}}_k)}{\partial {\mathcal{Z}}_k}\right]\right|}^{-1}\cdot {\mathcal{P}}_{init}({\mathcal{Z}}_{init})\right\}\\ & =\log {\mathcal{P}}_{init}({\mathcal{Z}}_{init})+\sum _{k=1}^{\mathcal{K}}\log \left\{{\left|\text{det}\left[\frac{\partial f_k({\mathcal{Z}}_k)}{\partial {\mathcal{Z}}_k}\right]\right|}^{-1}\right\}\end{array}$$

相关参考：
雅可比矩阵——百度百科
【机器学习白板推导系列(三十三) ~ 流模型(Flow Based Model)】