LeetCode练习四:栈
文章目录
- 一、 堆栈基础知识
- 1.1 简介
- 1.2 堆栈的顺序存储
- 1.2.1 堆栈顺序存储基本描述
- 1.2.2 堆栈顺序存储实现代码
- 1.3 堆栈的链式存储
- 1.3.1 堆栈的链式存储基本描述
- 1.3.2 堆栈的链式存储实现代码
- 二、 堆栈的基础应用
- 2.1 堆栈基础题列表
- 2.2 括号匹配问题
- 2.2.1 有效的括号
- 2.2.2 最长有效括号
- 2.3 前缀、中缀、后缀表达式
- 2.3.1 表达式简介
- 2.3.2 表达式转换原理
- 2.3.3 中缀转后缀算法
- 2.3.4 后缀表达式求值
- 2.4 表达式求值问题
- 2.4.1 基本计算器II
- 2.4.2 逆波兰表达式求值
- 2.4.3 基本计算器I
- 2.5 验证栈序列
- 三、单调栈
- 3.1 单调递增栈
- 3.2 单调递减栈
- 3.3 单调栈适用场景
- 3.3.1 寻找左侧第一个比当前元素大的元素
- 3.3.2 寻找左侧第一个比当前元素小的元素
- 3.3.3 寻找右侧第一个比当前元素大的元素
- 3.3.4 寻找右侧第一个比当前元素小的元素
- 四、 单调栈的应用
- 4.1 单调栈题目列表
- 4.2 下一个更大元素 I & II
- 4.3 每日温度
- 4.4 股票价格跨度
- 4.5 去除重复字母
- 4.6 柱状图中最大的矩形
- 4.7 接雨水
- 4.8 最大矩形
本文主要参考《算法通关手册》堆栈篇
一、 堆栈基础知识
1.1 简介
堆栈(Stack):简称为栈。一种线性表数据结构,是一种只允许在表的一端进行插入和删除操作的线性表。
我们把栈中允许插入和删除的一端称为 「栈顶(top)」;另一端则称为 「栈底(bottom)」。当表中没有任何数据元素时,称之为 「空栈」。
堆栈有两种基本操作:「插入操作」 和 「删除操作」。
- 栈的插入操作又称为「入栈」或者「进栈」。
- 栈的删除操作又称为「出栈」或者「退栈」。

简单来说,栈是一种 「后进先出(Last In First Out)」 的线性表,简称为 「LIFO 结构」。我们可以从两个方面来解释一下栈的定义:
-
「线性表」:栈首先是一个线性表,栈中元素具有前驱后继的线性关系。栈中元素按照 a1,a2,...,ana_1, a_2, ... , a_na1,a2,...,an 的次序依次进栈。栈顶元素为 ana_nan。
-
「后进先出原则」:根据堆栈的定义,每次删除的总是堆栈中当前的栈顶元素,即最后进入堆栈的元素。而在进栈时,最先进入堆栈的元素一定在栈底,最后进入堆栈的元素一定在栈顶。也就是说,元素进入堆栈或者退出退栈是按照「后进先出(Last In First Out)」的原则进行的。
堆栈的基本操作
栈作为一种线性表来说,理论上应该具备线性表所有的操作特性,但由于「后进先出」的特殊性,所以针对栈的操作进行了一些变化。尤其是插入操作和删除操作,改为了入栈(push)和出栈(pop)。
堆栈的基本操作如下:
-
初始化空栈:创建一个空栈,定义栈的大小
size,以及栈顶元素指针top。 -
判断栈是否为空:当堆栈为空时,返回
True。当堆栈不为空时,返回False。一般只用于栈中删除操作和获取当前栈顶元素操作中。 -
判断栈是否已满:当堆栈已满时,返回
True,当堆栈未满时,返回False。一般只用于顺序栈中插入元素和获取当前栈顶元素操作中。 -
插入元素(进栈、入栈):相当于在线性表最后元素后面插入一个新的数据元素。并改变栈顶指针
top的指向位置。 -
删除元素(出栈、退栈):相当于在线性表最后元素后面删除最后一个数据元素。并改变栈顶指针
top的指向位置。 -
获取栈顶元素:相当于获取线性表中最后一个数据元素。与插入元素、删除元素不同的是,该操作并不改变栈顶指针
top的指向位置。
接下来我们来看一下栈的顺序存储与链式存储两种不同的实现方式。
1.2 堆栈的顺序存储
和线性表类似,栈有两种存储表示方法:「顺序栈」 和 「链式栈」。
- 「顺序栈」:即堆栈的顺序存储结构。利用一组地址连续的存储单元依次存放自栈底到栈顶的元素,同时使用指针
top指示栈顶元素在顺序栈中的位置。 - 「链式栈」:即堆栈的链式存储结构。利用单链表的方式来实现堆栈。栈中元素按照插入顺序依次插入到链表的第一个节点之前,并使用栈顶指针
top指示栈顶元素,top永远指向链表的头节点位置。
堆栈最简单的实现方式就是借助于一个数组来描述堆栈的顺序存储结构。在 Python 中我们可以借助列表 list 来实现。这种采用顺序存储结构的堆栈也被称为 「顺序栈」。
1.2.1 堆栈顺序存储基本描述

我们约定 self.top 指向栈顶元素所在位置。
- 初始化空栈:使用列表创建一个空栈,定义栈的大小
self.size,并令栈顶元素指针self.top指向-1,即self.top = -1。 - 判断栈是否为空:当
self.top == -1时,说明堆栈为空,返回True,否则返回False。 - 判断栈是否已满:当
self.top == self.size - 1,说明堆栈已满,返回True,否则返回返回False。 - 插入元素(进栈、入栈):先判断堆栈是否已满,已满直接抛出异常。如果堆栈未满,则在
self.stack末尾插入新的数据元素,并令self.top向右移动1位。 - 删除元素(出栈、退栈):先判断堆栈是否为空,为空直接抛出异常。如果堆栈不为空,则删除
self.stack末尾的数据元素,并令self.top向左移动1位。 - 获取栈顶元素:先判断堆栈是否为空,为空直接抛出异常。不为空则返回
self.top指向的栈顶元素,即self.stack[self.top]。
1.2.2 堆栈顺序存储实现代码
class Stack:# 初始化空栈def __init__(self, size=100):self.stack = []self.size = sizeself.top = -1 # 判断栈是否为空def is_empty(self):return self.top == -1# 判断栈是否已满def is_full(self):return self.top + 1 == self.size# 入栈操作def push(self, value):if self.is_full():raise Exception('Stack is full')else:self.stack.append(value)self.top += 1# 出栈操作def pop(self):if self.is_empty():raise Exception('Stack is empty')else:self.stack.pop()self.top -= 1# 获取栈顶元素def peek(self):if self.is_empty():raise Exception('Stack is empty')else:return self.stack[self.top]
1.3 堆栈的链式存储
堆栈的顺序存储结构保留着顺序存储分配空间的固有缺陷,即在栈满或者其他需要重新调整存储空间时需要移动大量元素。为此,堆栈可以采用链式存储方式来实现。在 Python 中我们通过构造链表节点 Node 的方式来实现。这种采用链式存储结构的堆栈也被称为 「链式栈」。

1.3.1 堆栈的链式存储基本描述
我们约定 self.top 指向栈顶元素所在位置。
- 初始化空栈:使用列表创建一个空栈,并令栈顶元素指针
self.top指向None,即self.top = None。 - 判断栈是否为空:当
self.top == None时,说明堆栈为空,返回True,否则返回False。 - 插入元素(进栈、入栈):创建值为
value的链表节点,插入到链表头节点之前,并令栈顶指针self.top指向新的头节点。 - 删除元素(出栈、退栈):先判断堆栈是否为空,为空直接抛出异常。如果堆栈不为空,则先使用变量
cur存储当前栈顶指针self.top指向的头节点,然后令self.top沿着链表移动1位,然后再删除之前保存的cur节点。 - 获取栈顶元素:先判断堆栈是否为空,为空直接抛出异常。不为空则返回
self.top指向的栈顶节点的值,即self.top.value。
1.3.2 堆栈的链式存储实现代码
class Node:def __init__(self, value):self.value = valueself.next = Noneclass Stack:# 初始化空栈def __init__(self):self.top = None# 判断栈是否为空def is_empty(self):return self.top == None# 入栈操作def push(self, value):cur = Node(value)cur.next = self.topself.top = cur# 出栈操作def pop(self):if self.is_empty():raise Exception('Stack is empty')else:cur = self.topself.top = self.top.nextdel cur# 获取栈顶元素def peek(self):if self.is_empty():raise Exception('Stack is empty')else:return self.top.value
二、 堆栈的基础应用
堆栈是算法和程序中最常用的辅助结构,其的应用十分广泛。堆栈基本应用于两个方面:
- 使用堆栈可以很方便的保存和取用信息,因此长被用作算法和程序中的辅助存储结构,临时保存信息,供后面操作中使用。
- 例如:操作系统中的函数调用栈,浏览器中的前进、后退功能。
- 堆栈的后进先出规则,可以保证特定的存取顺序。
- 例如:翻转一组元素的顺序、铁路列车车辆调度。
2.1 堆栈基础题列表
| 题号 | 标题 | 题解 | 标签 | 难度 |
|---|---|---|---|---|
| 1047 | 删除字符串中的所有相邻重复项 | Python | 字符串、栈 | 简单 |
| 0155 | 最小栈 | Python | 栈、设计 | 简单 |
| 0020 | 有效的括号 | Python | 栈、字符串 | 简单 |
| 0227 | 基本计算器 II | Python | 栈、字符串 | 中等 |
| 0739 | 每日温度 | Python | 栈、哈希表 | 中等 |
| 0150 | 逆波兰表达式求值 | Python | 栈 | 中等 |
| 0232 | 用栈实现队列 | Python | 栈、设计 | 简单 |
| 剑指 Offer 09 | 用两个栈实现队列 | Python | 栈、设计、队列 | 简单 |
| 0394 | 字符串解码 | Python | 栈、深度优先搜索 | 中等 |
| 0032 | 最长有效括号 | Python | 栈、字符串、动态规划 | 困难 |
| 0946 | 验证栈序列 | Python | 栈、数组、模拟 | 中等 |
| 剑指 Offer 06 | 从尾到头打印链表 | Python | 栈、递归、链表、双指针 | 简单 |
| 0739 | 每日温度 | Python | 栈、哈希表 | 中等 |
| 0071 | 简化路径 |
下面我们来讲解一下栈应用的典型例子。
2.2 括号匹配问题
2.2.1 有效的括号
20. 有效的括号 - 力扣(LeetCode)
给定一个只包括 '(',')','{','}','[',']' 的字符串 s ,判断字符串 s 是否有效(即括号是否匹配)。
- 左括号必须用相同类型的右括号闭合。
- 左括号必须以正确的顺序闭合。
示例:
- 输入:s = “()[]{}”
- 输出:True
解题思路:括号匹配是「栈」的经典应用。我们可以用栈来解决这道题。
- 先判断一下字符串的长度是否为偶数。因为括号是成对出现的,所以字符串的长度应为偶数,可以直接判断长度为奇数的字符串不匹配。如果字符串长度为奇数,则说明字符串
s中的括号不匹配,直接返回False。 - 使用栈
stack来保存未匹配的左括号。然后依次遍历字符串s中的每一个字符。- 如果遍历到左括号时,将其入栈。
- 如果遍历到右括号时,先看栈顶元素是否是与当前右括号相同类型的左括号。
- 如果是与当前右括号相同类型的左括号,则令其出栈,继续向前遍历。
- 如果不是与当前右括号相同类型的左括号,则说明字符串
s中的括号不匹配,直接返回False。
- 遍历完,还要再判断一下栈是否为空。
- 如果栈为空,则说明字符串
s中的括号匹配,返回True。 - 如果栈不为空,则说明字符串
s中的括号不匹配,返回False。
- 如果栈为空,则说明字符串
代码
class Solution:def isValid(self, s: str) -> bool:if len(s) % 2 == 1:return Falsestack = list()for ch in s:if ch == '(' or ch == '[' or ch == '{':stack.append(ch)elif ch == ')':if len(stack) !=0 and stack[-1] == '(':stack.pop()else:return Falseelif ch == ']':if len(stack) !=0 and stack[-1] == '[':stack.pop()else:return Falseelif ch == '}':if len(stack) !=0 and stack[-1] == '{':stack.pop()else:return Falseif len(stack) == 0:return Trueelse:return False
- 时间复杂度:O(n)O(n)O(n)。
- 空间复杂度:O(1)O(1)O(1)。
2.2.2 最长有效括号
32 最长有效括号 - 力扣(LeetCode)
给你一个只包含 ‘(’ 和 ‘)’ 的字符串,找出最长有效(格式正确且连续)括号子串的长度。
示例:
- 输入:s = “)()())”
- 输出:4
- 解释:最长有效括号子串是 “()()”
参考官方题解,使用单调栈来解决。主要思路是我们始终保持栈底元素为当前已经遍历过的元素中,「最后一个没有被匹配的右括号的下标」。
- 对于遇到的每个 ‘
(’ ,直接入栈 - 对于遇到的每个 ‘
)’ ,我们先弹出栈顶元素表示匹配了当前右括号:- 如果栈为空,说明当前的右括号为没有被匹配的右括号,我们将其下标放入栈中来更新我们之前提到的「最后一个没有被匹配的右括号的下标」
- 如果栈不为空,当前右括号的下标减去栈顶元素即为,「以该右括号为结尾的最长有效括号的长度」。
我们从前往后遍历字符串并更新答案即可。
注意:如果一开始栈为空,第一个字符为左括号的时候,我们会将其放入栈中,这样就不满足提及的「最后一个没有被匹配的右括号的下标」,为了保持统一,我们在一开始的时候往栈中放入一个值为
−1的元素。
class Solution:def longestValidParentheses(self, s: str) -> int:stack=[-1] # 初始赋值为-1,这样匹配到都一个右括号时,长度=1-(-1)=2,刚刚好。ans=0for i in range(len(s)):if s[i]=="(":stack.append(i)else:stack.pop()if len(stack)==0:stack.append(i)else:ans=max(ans,i-stack[-1]) return ans
- 时间复杂度:O(n)O(n)O(n)。
- 空间复杂度:O(n)O(n)O(n)。
2.3 前缀、中缀、后缀表达式
2.3.1 表达式简介
- 中缀表达式
- 中缀表达式:操作符介于操作数之间的表达式。
- 中缀(infix)表达式:A + B * C + D ,为了避免计算顺序混淆,引入全括号表达式;
- 全括号中缀表达式:((A + (B * C)) + D),内层括号优先级更高。
- 前缀和后缀表达式
- 前缀(prefix)表达式:将操作符移到前面,形式变为:操作符、第一操作数、第二操作数。
- 后缀(postfix)表达式:将操作符移到后面,形式变为:第一操作数、第二操作数、操作符。

2.3.2 表达式转换原理
例:(A + (B * C))
- 中缀转后缀表达式:把操作符移到相应的右括号替代之,并删掉左括号
- 把操作符
*移到子表达式(B * C)的右括号位置替代它,再删去左括号得到BC* - 把操作符
+移到相应的右括号并删掉左括号,表达式就转为 后缀 形式,即:ABC*+。
- 把操作符
- 中缀转前缀表达式:同理,把操作符移到相应的左括号替代之,并删掉右括号,表达时就转换为 前缀 形式,即:
+A*BC。
总结:
- 前后缀表达式中,操作符顺序完全决定了运算的次序,多数情况下计算机用此方法,特别是后缀法。
- 离操作数越近的越先做
- 无论表达式多复杂,转换为前缀或后缀只需要两个步骤:
- 将中缀表达式转换为全括号形式;
- 将所有操作符移动到子表达式所在的左括号(前缀)或者右括号(后缀)处,替代之,再删除所有括号。
2.3.3 中缀转后缀算法
- 在中缀表达式转换为后缀形式的处理过程中,操作符比操作数要晚输出,所以在扫描到对应的第二个操作数之前,需要把操作符先保存起来;
- 而这些暂存的操作符,由于优先级的规则还有可能要反转次序输出。
在A+B*C中,+虽然先出现,但优先级比后面这个*要低,所以它要等*处理完后,才能再处理。 - 这种反转特性,使得我们考虑用
栈来保存暂时未处理的操作符。
总结下,在从左到右扫描逐个字符扫描中缀表达式的过程中,采用一个栈来暂存未处理的操作符。这样,栈顶的操作符就是最近暂存进去的,当遇到一个新的操作符,就需要跟栈顶的操作符比较下优先级,再行处理。
所以遇到左括号,要标记下,其后出现的操作符优先级提升了,一旦扫描到对应的右括号,就可以马上输出这个操作符
流程:
- 从左到右扫描中缀表达式单词列表
- 如果单词是操作数,则直接添加到后缀表达式列表的末尾;
- 如果单词是左括号,则压入opstack栈顶;
- 如果单词是右括号,则反复弹出opstack栈顶操作符,加入到输出列表末尾,直到碰到左括号;
- 如果单词是操作符,则压入opstack栈顶,但在压入栈顶之前,要比较其与栈顶操作符的优先级,如果栈顶的高于或等于它,就要反复弹出栈顶操作符,加入到输出列表末尾;直到栈顶的操作符优先级低于它。
- 中缀表达式单词列表扫描结束后,把opstack栈中的所有剩余操作符 依次弹出,添加到输出列表末尾。
- 把输出列表再用join方法合并成后缀表达式字符串,算法结束。
代码实现:
from pythonds.basic.stack import Stackdef infixToPostfix(infixexpr):prec = {}prec["*"] = 3prec["/"] = 3prec["+"] = 2prec["-"] = 2prec["("] = 1opStack = Stack()postfixList = []tokenList = infixexpr.split()for token in tokenList:if token in "ABCDEFGHIJKLMNOPQRSTUVWXYZ" or token in "0123456789":postfixList.append(token)elif token == '(':opStack.push(token)elif token == ')':topToken = opStack.pop()while topToken != '(':postfixList.append(topToken)topToken = opStack.pop()else:while (not opStack.isEmpty()) and \(prec[opStack.peek()] >= prec[token]):postfixList.append(opStack.pop())opStack.push(token)while not opStack.isEmpty():postfixList.append(opStack.pop())return " ".join(postfixList)
2.3.4 后缀表达式求值
- 创建空栈operandStack用于暂存操作数。
- 将后缀表达式用split方法解析为单词(token)的列表。
- 从左到右扫描单词列表,如果单词是一个操作数,将单词转换为整数int,压入operandStack栈顶;如果单词是一个操作符,就开始求值,从栈顶弹出两个操作数,先弹出的是右操作数,后弹出的是左操作数,计算后将值重新压入栈顶。
- 单词列表扫描结束后,表达式的值就在栈顶。
- 弹出栈顶的值,返回。

代码实现:
from pythonds.basic.stack import Stackdef postfixEval(postfixExpr):operandStack = Stack()tokenList = postfixExpr.split()for token in tokenList:if token in "0123456789":operandStack.push(int(token))else:operand2 = operandStack.pop()operand1 = operandStack.pop()result = doMath(token,operand1,operand2)operandStack.push(result)return operandStack.pop()def doMath(op,op1,op2):if op == "*":return op1 * op2elif op == "/":return op1 / op2elif op == "+":return op1 + op2else:return op1 - op2
2.4 表达式求值问题
2.4.1 基本计算器II
227. 基本计算器 II - 力扣(LeetCode)
给定一个字符串表达式 s,表达式中所有整数为非负整数,运算符只有 +、-、*、/,没有括号。请实现一个基本计算器来计算并返回它的值。
- 1≤s.length≤3∗1051 \le s.length \le 3 * 10^51≤s.length≤3∗105。
s由整数和算符(+、-、*、/)组成,中间由一些空格隔开。s表示一个有效表达式。- 表达式中的所有整数都是非负整数,且在范围 [0,231−1][0, 2^{31} - 1][0,231−1] 内。
- 题目数据保证答案是一个 32-bit 整数。
示例:
- 输入:s = “
3+2*2” - 输出:7
解题思路
计算表达式中,乘除运算优先于加减运算。我们可以先做所有的乘除运算,将其结果放回表达式的原位置,这样整个表达式的值,就成了一系列加减的结果。
- 遍历字符串,使用op记录每个数字之前的运算符。对于第一个数字,其之前的运算符视为‘+’。每次遍历到数字末尾时,根据op决定当前数字的计算方式:
+:直接入栈-:将数字的负数入栈*/:将栈顶数字弹出,计算其与当前数字的结果,再将计算结果入栈- 处理完当前数字后,更新操作符op,进行下一次计算
- 遍历完后,计算栈中所有数字的累加结果
class Solution:def calculate(self, s: str) -> int:s=list(s)stack=[]op='+' # 记录操作符,默认为+num=""for i in range(len(s)):if s[i].isdigit():num+=s[i]if i==len(s)-1 or s[i] in '+-*/':num=int(num)if op=='+':stack.append(num)elif op=='-':stack.append(-num)elif op=='*':stack.append(stack.pop()*num)elif op=='/':stack.append(int(stack.pop()/num))op=s[i]num=""return sum(stack)
2.4.2 逆波兰表达式求值
150. 逆波兰表达式求值
给你一个字符串数组 tokens ,表示一个根据 逆波兰表示法 表示的算术表达式。
- 两个整数之间的除法总是 向零截断
- 表达式中不含除零运算
- 输入是一个根据逆波兰表示法表示的算术表达式,有效的算符为 ‘+’、‘-’、‘*’ 和 ‘/’ 。
- 示例:
- 输入:tokens =
["10","6","9","3","+","-11","*","/","*","17","+","5","+"] - 输出:22
- 该算式转化为常见的中缀算术表达式为:
((10 * (6 / ((9 + 3) * -11))) + 17) + 5
- 输入:tokens =
本题实际是后缀表达式求值问题。因为前缀或者后缀表达式中,靠近数字的操作符先运算,所以不存在中缀表达式那种需要先比较运算符优先级的情况,直接运算就行了。唯一注意的是,数字可以是负数,需要稍微处理一下。
class Solution:def evalRPN(self, tokens: List[str]) -> int:Stack = [] for token in tokens:# 数字直接入栈,负数将其乘以-1再入栈if token.isdigit():Stack.append(int(token))elif token[0]=="-" and len(token)>1:# 此时表示的是负数Stack.append(int(token[1:])*-1)# 碰到操作符就开始运算,弹出的第一个栈顶元素是第二操作数 else: num2 = Stack.pop()num1 = Stack.pop()result = self.doMath(token,num1,num2)Stack.append(result)return Stack.pop()def doMath(self,op,num1,num2):if op == "*":return num1 * num2elif op == "/":return int(num1 / num2)elif op == "+":return num1 + num2else:return num1 - num2
2.4.3 基本计算器I
224. 基本计算器
给你一个字符串表达式 s ,请你实现一个基本计算器来计算并返回它的值。
- s 由数字、加减乘除和小括号 组成
- ‘+’ 不能用作一元运算,例如, “
+1” 和 “+(2 + 3)” 无效 - ‘-’ 可以用作一元运算,即 “
-1” 和 “-(2 + 3)” 是有效的 - 输入中不存在两个连续的操作符
- 示例:
- 输入:
s= "(1+(4+5+2)-3)+(6+8)" - 输出:23
- 输入:
解题思路一:括号展开+栈


class Solution:def calculate(self, s: str) -> int:ops = [1]sign = 1ret = 0n = len(s)i = 0while i < n:if s[i] == ' ':i += 1elif s[i] == '+':sign = ops[-1]i += 1elif s[i] == '-':sign = -ops[-1]i += 1elif s[i] == '(':ops.append(sign)i += 1elif s[i] == ')':ops.pop()i += 1else:num = 0while i < n and s[i].isdigit():num = num * 10 + ord(s[i]) - ord('0')i += 1ret += num * signreturn ret
解题思路2:构造nums和ops两个栈,分别存放操作数和操作符,然后遍历表达式:
参考《使用「双栈」解决「究极表达式计算」问题》
- 遇到空格,跳过
- 遇到数字,将连续数字直接在nums中入栈(负数乘以-1)
- 遇到右括号时,优先级最大,反复弹出ops和nums中的元素进行计算,直到遇到左括号,将结果存入nums中。
- 因为我们是从前往后做的,假设我们当前已经扫描到 2 + 1 了(此时栈内的操作为 + )。
- 遇到操作符,在ops中入栈。在放入之前先把栈内可以算的都算掉(只有「栈内运算符」比「当前运算符」优先级高/同等,才进行运算),使用现有的 nums 和 ops 进行计算,直到没有操作或者遇到左括号,计算结果放到 nums
- 以
2 + 1为例,如果后面出现的 + 2 或者 - 1 的话,满足「栈内运算符」比「当前运算符」优先级高/同等,可以将 2 + 1 算掉,把结果放到 nums 中; - 如果后面出现的是 * 2 或者 / 1 的话,不满足「栈内运算符」比「当前运算符」优先级高/同等,这时候不能计算 2 + 1。
- 由于第一个数可能是负数,为了减少边界判断。一个小技巧是先往 nums 添加一个 0
- 为防止 () 内出现的首个字符为运算符,将所有的空格去掉,并将 (- 替换为 (0-,(+ 替换为 (0+(当然也可以不进行这样的预处理,将这个处理逻辑放到循环里去做)
- 以
2.5 验证栈序列
946 验证栈序列
给定 pushed 和 popped 两个序列,每个序列中的 值都不重复,只有当它们可能是在最初空栈上进行的推入 push 和弹出 pop 操作序列的结果时,返回 true;否则,返回 false 。
- 示例 1:
- 输入:pushed = [1,2,3,4,5], popped = [4,5,3,2,1]
- 输出:true
- 解释:我们可以按以下顺序执行:
- push(1), push(2), push(3), push(4), pop() -> 4,
- push(5), pop() -> 5, pop() -> 3, pop() -> 2, pop() -> 1
- 示例 2:
- 输入:pushed = [1,2,3,4,5], popped = [4,3,5,1,2]
- 输出:false
- 解释:1 不能在 2 之前弹出。
使用分离双指针i和j,分别遍历pushed 和 popped两个数组。再用空栈存储每次操作的元素。
pushed[i]入栈,i右移- 当
popped[j]在栈中时,开始弹出,弹出前进行比较popped[j]等于栈顶元素时,栈顶元素出栈,j右移- 否则弹出次序不对,返回
False
class Solution:def validateStackSequences(self, pushed: List[int], popped: List[int]) -> bool:n=len(popped)stack=[]i,j=0,0# 分离双指针while i<n and j<n:stack.append(pushed[i])i+=1while stack and popped[j] in stack:if popped[j]==stack[-1]:j+=1stack.pop()else:return Falsereturn True
也可以写成:(popped[j]等于栈顶元素就出栈,遍历完看栈是否为空)
class Solution:def validateStackSequences(self, pushed: List[int], popped: List[int]) -> bool:n=len(popped)stack=[]i,j=0,0# 分离双指针while i<n and j<n:stack.append(pushed[i])i+=1while stack and popped[j]==stack[-1]:j+=1stack.pop() return len(stack)==0
三、单调栈
-
单调栈(Monotone Stack):一种特殊的栈。在栈的「先进后出」规则基础上,要求「从 栈顶 到 栈底 的元素是单调递增(或者单调递减)」。
-
单调递增栈:从栈顶到栈底的元素是单调递增的栈
-
单调递减栈:从栈顶到栈底的元素是单调递减的栈
注意:这里定义的顺序是从「栈顶」到「栈底」。有的文章里是反过来的。本文全文以「栈顶」到「栈底」的顺序为基准来描述单调栈。
3.1 单调递增栈
只有比栈顶元素小的元素才能直接进栈,否则需要先将栈中比当前元素小的元素出栈,再将当前元素入栈。 下面我们以数组 [2, 7, 5, 4, 6, 3, 4, 2] 为例,从左到右遍历,模拟一下「单调递增栈」的进栈、出栈过程:
| 第 i 步 | 待插入元素 | 操 作 | 结 果(左侧为栈底) | 作 用 |
|---|---|---|---|---|
| 1 | 2 | 2 入栈 | [2] | 元素 2 的左侧无比 2 大的元素 |
| 2 | 7 | 2 出栈,7 入栈 | [7] | 元素 7 的左侧无比 7 大的元素 |
| 3 | 5 | 5 入栈 | [7, 5] | 元素 5 的左侧第一个比 5 大的元素为:7 |
| 4 | 4 | 4 入栈 | [7, 5, 4] | 元素 4 的左侧第一个比 4 大的元素为:5 |
| 5 | 6 | 4 出栈,5 出栈,6 入栈 | [7, 6] | 元素 6 的左侧第一个比 6 大的元素为:7 |
| 6 | 3 | 3 入栈 | [7, 6, 3] | 元素 3 的左侧第一个比 3 大的元素为:6 |
| 7 | 4 | 3 出栈,4 入栈 | [7, 6, 4] | 元素 4 的左侧第一个比 4 大的元素为:6 |
| 8 | 2 | 2 入栈 | [7, 6, 4, 2] | 元素 2 的左侧第一个比 2 大的元素为:4 |
最终栈中元素为 [7, 6, 4, 2]。因为从栈顶(右端)到栈底(左侧)元素的顺序为 2, 4, 6, 7,满足递增关系,所以这是一个单调递增栈。
我们以上述过程第 5 步为例,所对应的图示过程为:
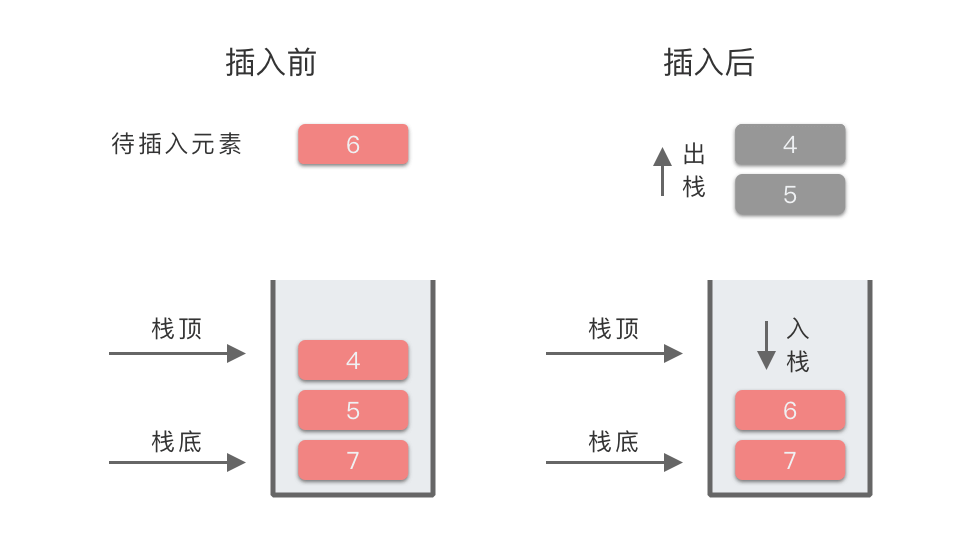
以从左到右遍历元素为例,单调递增栈伪代码为:
def monotoneIncreasingStack(nums):stack = []for num in nums:while stack and num >= stack[-1]:stack.pop()stack.append(num)
3.2 单调递减栈
只有比栈顶元素大的元素才能直接进栈,否则需要先将栈中比当前元素大的元素出栈,再将当前元素入栈。下面我们以数组 [4, 3, 2, 5, 7, 4, 6, 8] 为例,模拟一下「单调递减栈」的进栈、出栈过程:
| 第 i 步 | 待插入元素 | 操 作 | 结 果(左侧为栈底) | 作用 |
|---|---|---|---|---|
| 1 | 4 | 4 入栈 | [4] | 元素 4 的左侧无比 4 小的元素 |
| 2 | 3 | 4 出栈,3 入栈 | [3] | 元素 3 的左侧无比 3 小的元素 |
| 3 | 2 | 3 出栈,2 入栈 | [2] | 元素 2 的左侧无比 2 小的元素 |
| 4 | 5 | 5 入栈 | [2, 5] | 元素 5 的左侧第一个比 5 小的元素是:2 |
| 5 | 7 | 7 入栈 | [2, 5, 7] | 元素 7 的左侧第一个比 7 小的元素是:5 |
| 6 | 4 | 7 出栈,5 出栈,4 入栈 | [2, 4] | 元素 4 的左侧第一个比 4 小的元素是:2 |
| 7 | 6 | 6 入栈 | [2, 4, 6] | 元素 6 的左侧第一个比 6 小的元素是:4 |
| 8 | 8 | 8 入栈 | [2, 4, 6, 8] | 元素 8 的左侧第一个比 8 小的元素是:6 |
最终栈中元素为 [2, 4, 6, 8]。因为从栈顶(右端)到栈底(左侧)元素的顺序为 8, 6, 4, 2,满足递减关系,所以这是一个单调递减栈。
我们以上述过程第 6 步为例,所对应的图示过程为:

以从左到右遍历元素为例,单调递减栈伪代码为:
def monotoneDecreasingStack(nums):stack = []for num in nums:while stack and num <= stack[-1]:stack.pop()stack.append(num)
3.3 单调栈适用场景
单调栈可以在时间复杂度为 O(n)O(n)O(n) 的情况下,求解出某个元素左边或者右边第一个比它大或者小的元素。
所以单调栈一般用于解决一下几种问题:
- 寻找左侧第一个比当前元素大的元素。
- 寻找左侧第一个比当前元素小的元素。
- 寻找右侧第一个比当前元素大的元素。
- 寻找右侧第一个比当前元素小的元素。
下面分别说一下这几种问题的求解方法。
3.3.1 寻找左侧第一个比当前元素大的元素
- 从左到右遍历元素,构造单调递增栈(从栈顶到栈底递增):
- 一个元素左侧第一个比它大的元素就是将其「插入单调递增栈」时的栈顶元素。
- 如果插入时的栈为空,则说明左侧不存在比当前元素大的元素。
3.3.2 寻找左侧第一个比当前元素小的元素
- 从左到右遍历元素,构造单调递减栈(从栈顶到栈底递减):
- 一个元素左侧第一个比它小的元素就是将其「插入单调递减栈」时的栈顶元素。
- 如果插入时的栈为空,则说明左侧不存在比当前元素小的元素。
3.3.3 寻找右侧第一个比当前元素大的元素
-
从左到右遍历元素,构造单调递增栈(从栈顶到栈底递增):
- 一个元素右侧第一个比它大的元素就是将其「弹出单调递增栈」时即将插入的元素。
- 如果该元素没有被弹出栈,则说明右侧不存在比当前元素大的元素。
-
从右到左遍历元素,构造单调递增栈(从栈顶到栈底递增):
- 一个元素右侧第一个比它大的元素就是将其「插入单调递增栈」时的栈顶元素。
- 如果插入时的栈为空,则说明右侧不存在比当前元素大的元素。
3.3.4 寻找右侧第一个比当前元素小的元素
-
从左到右遍历元素,构造单调递减栈(从栈顶到栈底递减):
- 一个元素右侧第一个比它小的元素就是将其「弹出单调递减栈」时即将插入的元素。
- 如果该元素没有被弹出栈,则说明右侧不存在比当前元素小的元素。
-
从右到左遍历元素,构造单调递减栈(从栈顶到栈底递减):
- 一个元素右侧第一个比它小的元素就是将其「插入单调递减栈」时的栈顶元素。
- 如果插入时的栈为空,则说明右侧不存在比当前元素小的元素。
上边的分类解法有点绕口,可以简单记为以下条规则:
-
无论哪种题型,都建议从左到右遍历元素。
-
查找 「比当前元素大的元素」 就用 单调递增栈,查找 「比当前元素小的元素」 就用 单调递减栈。
-
从 「左侧」 查找就看 「插入栈」 时的栈顶元素,从 「右侧」 查找就看 「弹出栈」 时即将插入的元素。
四、 单调栈的应用
4.1 单调栈题目列表
| 题号 | 标题 | 题解 | 标签 | 难度 |
|---|---|---|---|---|
| 0739 | 每日温度 | Python | 栈、哈希表 | 中等 |
| 0496 | 下一个更大元素 I | Python | 栈、数组、哈希表、单调栈 | 简单 |
| 0503 | 下一个更大元素 II | Python | 栈、数组、单调栈 | 中等 |
| 0901 | 股票价格跨度 | Python | 栈、设计、数据流、单调栈 | 中等 |
| 0084 | 柱状图中最大的矩形 | Python | 栈、数组、单调栈 | 困难 |
| 0316 | 去除重复字母 | Python | 栈、贪心、字符串、单调栈 | 中等 |
| 1081 | 不同字符的最小子序列 | Python | 栈、贪心、字符串、单调栈 | 中等 |
| 0042 | 接雨水 | Python | 栈、数组、双指针、动态规划、单调栈 | 困难 |
| 0085 | 最大矩形 | 单调栈 | 困难 |
下面介绍一下经典题目
4.2 下一个更大元素 I & II
- 0496. 下一个更大元素 I
- 0503. 下一个更大元素 II
给定两个没有重复元素的数组 nums1 和 nums2 ,其中 nums1 是 nums2 的子集。要求找出 nums1 中每个元素在 nums2 中的下一个比其大的值,如果不存在,对应位置输出 -1。
示例 :
- 输入:nums1 = [4,1,2], nums2 = [1,3,4,2].
- 输出:[-1,3,-1]
- 解释:nums1 中每个值的下一个更大元素如下所述:
- 4 ,用加粗斜体标识,nums2 = [1,3,4,2]。不存在下一个更大元素,所以答案是 -1 。
- 1 ,用加粗斜体标识,nums2 = [1,3,4,2]。下一个更大元素是 3 。
- 2 ,用加粗斜体标识,nums2 = [1,3,4,2]。不存在下一个更大元素,所以答案是 -1 。
解题思路
-
暴力求解:
根据题意直接暴力求解。遍历nums1中的每一个元素。对于nums1的每一个元素nums1[i],再遍历一遍nums2,查找nums2中对应位置右边第一个比nums1[i]大的元素。这种解法的时间复杂度是 O(n2)O(n^2)O(n2)。 -
使用单调递增栈。因为
nums1是nums2的子集,所以我们可以先遍历一遍nums2,并构造单调递增栈,求出nums2中每个元素右侧下一个更大的元素。然后将其存储到哈希表中。然后再遍历一遍nums1,从哈希表中取出对应结果,存放到答案数组中。这种解法的时间复杂度是 O(n)O(n)O(n)。
解题步骤
-
使用数组
ans存放答案。使用stack表示单调递增栈。使用哈希表d用于存储nums2中下一个比当前元素大的数值,映射关系为当前元素值:下一个比当前元素大的数值。 -
遍历数组
nums2,对于当前元素:- 如果当前元素值较小,则直接让当前元素值入栈。
- 如果当前元素值较大,则一直出栈,直到当前元素值小于栈顶元素。
- 出栈时,出栈元素是第一个大于当前元素值的元素。则将其映射到
d中。
- 出栈时,出栈元素是第一个大于当前元素值的元素。则将其映射到
-
遍历完数组
nums2,建立好所有元素下一个更大元素的映射关系之后,再遍历数组nums1。 -
从
d中取出对应的值,将其加入到答案数组中,最终输出答案数组ans。
代码
class Solution:def nextGreaterElement(self, nums1: List[int], nums2: List[int]) -> List[int]:stack=[]d=dict()ans=[]for i in nums2:while stack and i>stack[-1]: d[stack[-1]]=istack.pop()stack.append(i)for j in nums1:ans.append(d.get(j,-1))return ans
类似的题目还有下一个更大元素 I I,唯一不同的是数组是循环的。简单做法是将nums循环一次,即nums=nums+nums,再求解后,取结果的前m个数值作为答案:
class Solution:def nextGreaterElements(self, nums: List[int]) -> List[int]:m=len(nums)nums=nums+nums n=len(nums)stack=[]ans=[-1]*nfor i in range(n):while stack and nums[i]>nums[stack[-1]]:index=stack.pop()ans[index]=nums[i]stack.append(i)return ans[:m]
上面代码中 index=stack.pop()等同于
index=stack[-1]
stack.pop()
4.3 每日温度
739. 每日温度 - 力扣(LeetCode)
给定一个整数数组 temperatures ,表示每天的温度,返回一个数组 answer ,其中 answer[i] 是指对于第 i 天,下一个更高温度出现在几天后。如果气温在这之后都不会升高,请在该位置用 0 来代替。
- 1≤temperatures.length≤1051 \le temperatures.length \le 10^51≤temperatures.length≤105。
- 30≤temperatures[i]≤10030 \le temperatures[i] \le 10030≤temperatures[i]≤100。
示例:
- 输入: temperatures = [73,74,75,71,69,72,76,73]
- 输出: [1,1,4,2,1,1,0,0]
解题思路
本题就是寻找每个元素右侧第一个更大的元素,然后返回「该元素」与「右侧第一个比当前元素更大的元素」之间的距离,将所有距离保存为数组返回结果。考虑使用「单调递增栈」,栈中保存元素的下标。
详细步骤
- 将答案数组
ans全部赋值为 0。然后遍历数组每个位置元素。 - 如果栈为空,则将当前元素的下标入栈。
- 如果栈不为空,且当前数字大于栈顶元素对应数字,则栈顶元素出栈,并计算下标差。
- 此时当前元素就是栈顶元素的下一个更高值,将其下标差存入答案数组
ans中保存起来,判断栈顶元素。 - 直到当前数字小于或等于栈顶元素,则停止出栈,将当前元素下标入栈。
- 最后输出答案数组
ans。
代码
class Solution:def dailyTemperatures(self, temperatures: List[int]) -> List[int]:stack=[]n=len(temperatures)ans=[0]*nfor i in range(n):while stack and temperatures[i]>temperatures[stack[-1]]:index=stack.pop()ans[index]=i-indexstack.append(i)return ans
4.4 股票价格跨度
0901. 股票价格跨度
设计一个算法收集某些股票的每日报价,并返回该股票当日价格的跨度 。当日股票价格的跨度被定义为股票价格小于或等于今天价格的最大连续日数(从今天开始往回数,包括今天)。
实现 StockSpanner 类:
StockSpanner():初始化类对象。int next(int price):给出今天的股价price,返回该股票当日价格的 跨度 。
示例
- 输入: [100,80,60,70,60,75,85]
- 输出:那么股票跨度将是 [1,1,1,2,1,4,6] 。
解题思路
「求解小于或等于今天价格的最大连续日」等价于「求出左侧第一个比当前股票价格大的股票,并计算距离」。求出左侧第一个比当前股票价格大的股票我们可以使用「单调递减栈」来做。
详细步骤
-
初始化方法:初始化一个空栈,即
self.stack = [] -
求解今天股票价格的跨度:
-
初始化跨度
span为1。 -
如果今日股票价格
price大于等于栈顶元素self.stack[-1][0],则:- 将其弹出,即
top = self.stack.pop()。 - 跨度累加上弹出栈顶元素的跨度,即
span += top[1]。 - 继续判断,直到遇到一个今日股票价格
price小于栈顶元素的元素位置,再将[price, span]压入栈中。
- 将其弹出,即
-
如果今日股票价格
price小于栈顶元素self.stack[-1][0],则直接将[price, span]压入栈中。 -
最后输出今天股票价格的跨度
span。
-
代码
class StockSpanner:def __init__(self):self.stack = []def next(self, price: int) -> int:span = 1while self.stack and price >= self.stack[-1][0]:top = self.stack.pop()span += top[1]self.stack.append([price, span])return span
也可以将遍历时每个元素的下标 self.cur存入栈中,然后计算入栈时,当前元素下标和入栈前栈顶元素的下标差就行:
class StockSpanner:def __init__(self):#单调递增插入栈。左侧第一个更大的元素就是插入元素时的栈顶元素self.stack = [(inf,-1)]self.cur=-1 # 遍历时的当前元素下标,赋值为-1,第一次遍历时下标=0def next(self, price: int) -> int:self.cur+=1 # 第一个元素下标为0while self.stack and price>=self.stack[-1][0]: self.stack.pop() self.stack.append([price,self.cur])# 当前元素已入栈,所以其插入前的栈顶元素是stack[-2]return self.cur-self.stack[-2][1]
4.5 去除重复字母
0316. 去除重复字母 ,这道题和1081. 不同字符的最小子序列是一样的。
给你一个字符串 s ,请你去除字符串中重复的字母,使得每个字母只出现一次。需保证 返回结果的字典序最小(要求不能打乱其他字符的相对位置)。
示例:
- 输入:s = “cbacdcbc”
- 输出:“acdb”
解题思路
- 去重:可以通过 「使用哈希表存储字母出现次数」 的方式,将每个字母出现的次数统计起来,再遍历一遍,去除重复的字母。
- 不能打乱其他字符顺序:按顺序遍历,将非重复的字母存储到答案数组或者栈中,最后再拼接起来,就能保证不打乱其他字符顺序。
- 字典序最小:意味着字典序小的字母应该尽可能放在前面。
- 对于第
i个字符s[i]而言,如果第0~i - 1之间的某个字符s[j]在s[i]之后不再出现了,那么s[j]必须放到s[i]之前。 - 而如果
s[j]在之后还会出现,并且s[j]的字典序大于s[i],我们则可以先舍弃s[j],把s[i]尽可能的放到前面。后边再考虑使用s[j]所对应的字符。
- 对于第
要满足第 3 条需求,我们可以使用 「单调递减栈」 来解决,即使用单调栈存储 s[i] 之前出现的非重复、并且字典序最小的字符序列。整个算法步骤如下:
- 先遍历一遍字符串,用哈希表
d统计出每个字母出现的次数。 - 然后使用单调递减栈保存当前字符之前出现的非重复、并且字典序最小的字符序列。
- 当遍历到
s[i]时,如果s[i]没有在栈中出现过:- 比较
s[i]和栈顶元素stack[-1]的字典序。如果s[i]的字典序小于栈顶元素stack[-1],并且栈顶元素次数>1,则将栈顶元素弹出,并从哈希表d中减去栈顶元素出现的次数,继续遍历。 - 直到栈顶元素出现次数为
1时停止弹出。此时将s[i]添加到单调栈中。
- 比较
- 如果 遍历时,
s[i]在栈中出现过,就将其次数-1,因为我们只在s[i]首次遍历时将其入栈,后续重复时不入栈,其统计次数应该-1。 - 最后将单调栈中的字符依次拼接为答案字符串,并返回。
class Solution:def removeDuplicateLetters(self, s: str) -> str:from collections import Counterd=dict(Counter(s))# 使用单调递减栈保证字典序最小# 如果遍历的当前元素小于栈顶元素,当其次数大于1时,将栈顶弹出,对应次数-1。直至=0时不再弹出stack=[]for ch in s:if ch not in stack:while stack and ch<stack[-1] and d[stack[-1]]>1:# 注意,这里是先统计次数,再执行pop操作,并且是ch<=stack[-1]d[stack[-1]]-=1stack.pop() stack.append(ch)# 如果ch已经在栈中,将其次数-1,等同于之前的相同元素会出栈,当前重复元素入栈。# 否则[bbcaac]这种会出错。else: d[ch]-=1return "".join(stack)
4.6 柱状图中最大的矩形
0084. 柱状图中最大的矩形
给定一个非负整数数组 heights ,heights[i] 用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。要求计算出在该柱状图中,能够勾勒出来的矩形的最大面积。
示例
- 输入:heights = [2,1,5,6,2,3]
- 输出:10
- 解释:最大的矩形为图中红色区域,面积为 10
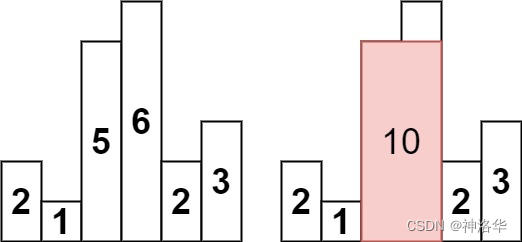
解题思路
-
暴力枚举「宽度」:
一重循环枚举所有柱子,第二重循环遍历柱子右侧的柱子,所得的宽度就是两根柱子形成区间的宽度,高度就是这段区间中的最小高度。然后计算出对应面积,记录并更新最大面积。这样下来,时间复杂度为 O(n2)O(n^2)O(n2)。 -
暴力枚举枚举「高度」。一重循环枚举所有柱子,以柱子高度为当前矩形高度,然后向两侧延伸,遇到小于当前矩形高度的情况就停止。然后计算当前矩形面积,记录并更新最大面积。这样下来,时间复杂度也是 O(n2)O(n^2)O(n2)。
-
单调栈遍历,求左右边界
- 当前柱子
heights[i]所能延伸到的最大面积S[i],其实就是左右两侧高度不小于heights[i]的最远柱子之间的面积。也就是说,柱子i往左右延伸,直到碰到的柱子高度<heights[i]时停止。所以本题关键是求数组heights中,每个元素左侧最近的更小值和右侧最近的更小值,考虑使用单调递减栈求解。 - 注意,面积延伸时,碰到更小的高度才停止,所以使用严格单调递减栈,遍历的元素严格大于栈顶元素才入栈,小于等于栈顶元素时,栈顶弹出。所以判断条件是
heights[i]<=heights[stack[-1]],有等号。
- 当前柱子
class Solution:def largestRectangleArea(self, heights: List[int]) -> int:stack=[]n=len(heights)# 寻找左侧更小值,使用单调递减插入栈,栈中只存入栈元素的下标。# 当前元素≤栈顶元素时,栈顶弹出。# 直到当前元素入栈,此时栈顶元素就是当前元素的左侧第一个更小值。# 如果碰到空栈,说明左侧没有更小的元素,将其下标记为-1(哨兵,表示往左可以延伸到数组开头)left=[-1]*n for i in range(n):while stack and heights[i]<=heights[stack[-1]]:stack.pop() left[i]=stack[-1] if stack else -1stack.append(i)# print(left)right=[n]*nstack=[] # 没有重新设置stack初始化,坑# 寻找右侧更小值,使用单调递减弹出栈# 当前元素≤栈顶元素时,将栈顶弹出。此时,弹出前的栈顶元素的右侧第一个更小值就是当前元素# 如果为空栈,说明右侧没有更小元素,将其下标记为n(也就是往右遍历到数组结尾)for i in range(n):while stack and heights[i]<=heights[stack[-1]]: right[stack[-1]]=i if stack else nstack.pop() stack.append(i)# print(right) ans = [(right[i]-left[i]-1) * heights[i] for i in range(n)] return max(ans)
上面的代码中,我们用插入栈得到左侧更小的元素,使用弹出栈得到右侧更小的元素,但都使用了单调递减栈,判断条件也相同,所以其实可以一次遍历得到左右边界,优化后代码为:
class Solution:def largestRectangleArea(self, heights: List[int]) -> int:stack=[]n=len(heights)left=[-1]*n right=[n]*n for i in range(n):while stack and heights[i]<=heights[stack[-1]]:right[stack[-1]]=i stack.pop() left[i]=stack[-1] if stack else -1stack.append(i)ans = [(right[i]-left[i]-1) * heights[i] for i in range(n)] if n > 0 else 0return max(ans)
4.7 接雨水
0042. 接雨水
给定n个非负整数组成的数组 height ,其表示表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
- 输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
- 输出:6
- 解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。

- n==height.lengthn == height.lengthn==height.length。
- 1≤n≤2∗1041 \le n \le 2 * 10^41≤n≤2∗104。
- 0≤height[i]≤1050 \le height[i] \le 10^50≤height[i]≤105。
解题思路
-
求出蓄水边界
- 最明显的,某个柱子左右有更高的柱子时,这个柱子上才可以接雨水 ,这样需要首先求出数组中每个元素左侧和右侧最近的更高柱子,即蓄水的左右边界。
- 所以考虑使用单调递增栈求出左右边界的下标。比如
height = [0,1,0,2,1,0,1,3,2,1,2,1]时,左边界left=[-1, -1, 1, -1, 3, 4, 3, -1, 7, 8, 7, 10],右边界right=[1, 3, 3, 7, 7, 6, 7, 12, 12, 10, 12, 12] - 寻找左右边界时,因为是寻找两侧严格大的柱子,判断条件不一样,没办法一次遍历出来(可以自行测试)。
-
求出蓄水面积
- 蓄水宽度=左右边界下标差,蓄水高度=min(左右边界高度)- 当前柱子高度。这样可以算出每个柱子可以接的雨水。
- 还是以上面例子为例,此时得到的结果ans(柱子下标i,接水面积area)=
[(2,1),(4,3),(5,1),(6,3),(9,1)]。可见计算的结果都是对的,唯一错误是下标4和6的这两个柱子,蓄水面积都计算了一次。观察可以发现,这两个柱子的左右边界完全相同,其结果只需要计算一次 - 考虑使用字典
d,存储每个柱子的边界。对于相同的边界,蓄水面积只计算一次。
class Solution:def trap(self, height: List[int]) -> int:#寻找左边界n=len(height)stack=[]# 构造单调递增栈,更小的元素才入栈。例如[8,3,3,7.7,9],当第一个3入栈时,7才是右侧更大的元素,所以是当前元素严格大于栈顶元素才入栈left,right=[-1]*n,[n]*nfor i in range(n):while stack and height[i]>height[stack[-1]]:right[stack[-1]]=i stack.pop() #left[i]=stack[-1] if stack else -1stack.append(i)stack=[] # 构造单调递增栈,更小的元素才入栈。例如[8,3,3],当第二个3入栈时,8才是左侧更大的元素# 所以判断条件中有等号,相同元素也要弹出。for i in range(n):while stack and height[i]>=height[stack[-1]]:stack.pop()left[i]=stack[-1] if stack else -1stack.append(i)print("left:",left)print("right:",right)# 如果碰到左右边界完全一样,只计算一次ans=[]d=dict()for i in range(n):# 遍历每个元素的左右边界l,r=left[i],right[i]if l!=-1 and r!=n: if (l,r) not in d: # 相同边界的柱子蓄水量只计算一次area=(min(height[l],height[r])-height[i])*(right[i]-left[i]-1)ans.append(area)#print(i,area)d[(l,r)]=ireturn sum(ans)
优化一:一次遍历出左右边界
上面代码可以优化,其实无论是height[i]>=height[stack[-1]]还是height[i]>height[stack[-1]],只用一个判断条件得到的结果,有一个边界是不完全准确的,但是不影响最终结果。比如:
height[i]>height[stack[-1]]时,左边界不准,为left= [-1, -1, 1, -1, 3, 4, 4(3), -1, 7, 8, 8(7), 10],右边界是准的,right= [1, 3, 3, 7, 7, 6, 7, 12, 12, 10, 12, 12]。- 上面第6个柱子左边界应该是3,这里判断是4。结果就是计算时,左边界4和柱子6的高度一样,area=0。所以,虽然不是严格的左边界,但是不影响最终结果。以上面数组为例,
area=[(2,1),(4,3),(5,1),(6,0),(9,1)]
class Solution:def trap(self, height: List[int]) -> int:#寻找左右边界n=len(height)stack=[]# 构造单调递增栈,更小的元素才入栈。例如[8,3,3,7.7,9],当第一个3入栈时,7才是右侧更大的元素,所以是当前元素严格大于栈顶元素才入栈# 例如[8,3,3],当第二个3入栈时,8才是左侧更大的元素left,right=[-1]*n,[n]*nfor i in range(n):while stack and height[i]>height[stack[-1]]: # 这里可以是≥right[stack[-1]]=i stack.pop() left[i]=stack[-1] if stack else -1stack.append(i)# print("left:",left)# print("right:",right)ans=[] for i in range(n):# 遍历每个元素的左右边界l,r=left[i],right[i]if l!=-1 and r!=n: area=(min(height[l],height[r])-height[i])*(right[i]-left[i]-1)ans.append(area)# print(i,area)return sum(ans)
优化二:在一次遍历中求左右边界,并同时求出蓄水面积
这里需要将判断条件左右边界不为数组头尾(if l!=-1 and r!=n: ) ,改为if stack,因为只有遇到空栈,才说明左右侧没有更高的柱子。
class Solution:def trap(self, height: List[int]) -> int:ans = 0stack = []size = len(height)for i in range(size):# 这里写成height[i] >= height[stack[-1]]也是没有问题的while stack and height[i] > height[stack[-1]]:cur = stack.pop(-1)# 当前元素被弹出时,其上一个元素是左侧更大值,将要入栈的是右侧更大值if stack:left = stack[-1] right = i high = min(height[i], height[stack[-1]]) - height[cur]ans += high * (right - left - 1)else: # 遇到空栈,停止弹出,跳出循环breakstack.append(i)return ans
4.8 最大矩形
0085:最大矩阵 ,参考题解《Python3 前缀和+单调栈计算最大矩形》
给定一个仅包含 0 和 1 ,大小为 rows x cols 的二维二进制矩阵,找出只包含 1 的最大矩形,并返回其面积。
示例:
-
输入:matrix = [[“1”,“0”,“1”,“0”,“0”],[“1”,“0”,“1”,“1”,“1”],[“1”,“1”,“1”,“1”,“1”],[“1”,“0”,“0”,“1”,“0”]]
-
输出:6
-
解释:最大矩形如下图所示。

解题思路 :
-
我们可以统计每一行中,每个元素上方“1”的个数,这样就等同于得到了每一行柱子的高度
height。- 对于
height的计算,根据最大前缀和思想,当前位置j为‘0’,则height[j]=0,当前位置为‘1’,则需要加上上一层连续1的个数,即height[j]+=1。 - 例如本题中,
height[2]=[3, 1, 3, 2, 2]
- 对于
-
用0084. 柱状图中最大的矩形中同样的做法,求得柱状图的最大面积就行。例如示例中,第二行面积为
[3, 5, 3, 6, 2] -
遍历每一行,得到各行的最大面积,取全局最大值就行。
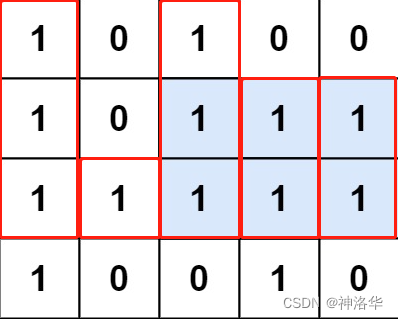
class Solution:def maximalRectangle(self, matrix: List[List[str]]) -> int:m,n=len(matrix),len(matrix[0])height=[0]*n # 每行上方1的个数,可视作柱子的高度ans=[] # 存储每行的最大面积for i in range(m):for j in range(n):# 第m行每个位置含1的高度height[j]=height[j]+1 if matrix[i][j]=="1" else 0#根据柱子高度计算最大面积,等同于第84题stack=[]left,right=[-1]*n,[n]*nfor h in range(n):while stack and height[h]<height[stack[-1]]:right[stack[-1]]=hstack.pop()left[h]=stack[-1] if stack else -1stack.append(h)res=[(right[h]-left[h]-1)*height[h] for h in range(n)] ans.append(max(res))return max(ans)
相关文章:

LeetCode练习四:栈
文章目录一、 堆栈基础知识1.1 简介1.2 堆栈的顺序存储1.2.1 堆栈顺序存储基本描述1.2.2 堆栈顺序存储实现代码1.3 堆栈的链式存储1.3.1 堆栈的链式存储基本描述1.3.2 堆栈的链式存储实现代码二、 堆栈的基础应用2.1 堆栈基础题列表2.2 括号匹配问题2.2.1 有效的括号2.2.2 最长…...

【Python实战】爬虫教程千千万,一到实战全完蛋?今天手把手教你一键采集某网站图书信息数据啦~排名第一的竟是...(爬虫+数据可视化)
前言 一本本书,是一扇扇窗,为追求知识的人打开认知世界的窗口 一本本书,是一双双翅膀,让追求理想的人张开翅膀翱翔 所有文章完整的素材源码都在👇👇 粉丝白嫖源码福利,请移步至CSDN社区或文末…...

【数据结构】堆的详解
本章的知识需要有树等相关的概念,如果你还不了解请先看这篇文章:初识二叉树 堆的详解一、二叉树的顺序结构及实现1、二叉树的顺序结构2、堆的概念及结构二、堆的简单实现 (以大堆为例)1、堆的定义2、堆的初始化3、堆的销毁4、堆的打印5、堆的插入6、堆顶元素的获取7…...

New Bing怼人、说谎、PUA,ChatGPT已经开始胡言乱语了
最近,来自大洋彼岸那头的ChatGPT科技浪潮席卷而来,微软将chatGPT整合搜索引擎Bing开启内测后,数百万用户蜂拥而至,都想试试这个「百事通」。 赶鸭子上架,“翻车”了? 但短短上线十几天,嵌入了…...
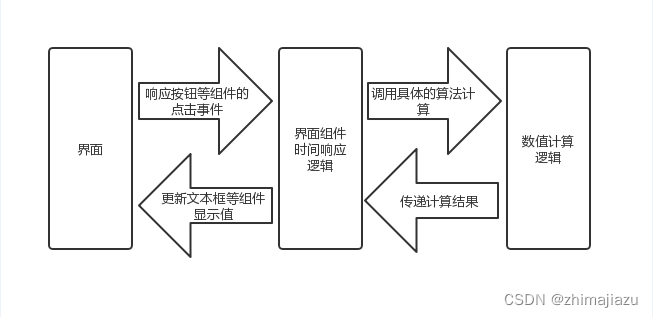
简易计算器-课后程序(JAVA基础案例教程-黑马程序员编著-第十一章-课后作业)
【案例11-2】 简易计算器 【案例介绍】 1.案例描述 本案例要求利用Java Swing 图形组件开发一个可以进行简单的四则运算的图形化计算器。 2.运行结果 运行结果 【案例分析】 要制作一个计算器,首先要知道它由哪些部分组成,如下图所示: 一…...
)
chatGPT使用:询问简历和面试相关话题(持续更新中)
chatGPT使用:询问简历和面试相关话题 写一份Java简历,价值2万元包装上面的Java简历面试自我介绍面试简述稿包装简历的方法技巧如何进行良好的自我介绍如何写一份优秀的面试简述稿如何写一份优秀的简历如何写一份优秀的面试讲述稿如何提高面试录取率如何拿到offer写一份Java简…...

Java的 Stream流
Stream流?结合Lambda表达式,用于简化集合和数组操作的API。Stream流的一个小例子:创建一个集合,存储多个姓名,把集合中所有以"张"开头的长度为3的元素存储到一个新的集合并输出。List<String> namesne…...
FL Studio 21 中文正式版发布支持多种超个性化主题
万众期待的 FL Studio 21 版本正式发布上线,目前在紧锣密鼓的安排上线中,届时所有购买正版 FL Studio 的用户,都可以免费升级到21版! 按照惯例,本次新版也会增加全新插件,来帮助大家更好地创作。今天先给大…...

【微信小程序】-- 全局配置 -- window - 导航栏(十五)
💌 所属专栏:【微信小程序开发教程】 😀 作 者:我是夜阑的狗🐶 🚀 个人简介:一个正在努力学技术的CV工程师,专注基础和实战分享 ,欢迎咨询! &…...
Spring中最常用的11个扩展点
前言我们一说到spring,可能第一个想到的是 IOC(控制反转) 和 AOP(面向切面编程)。没错,它们是spring的基石,得益于它们的优秀设计,使得spring能够从众多优秀框架中脱颖而出。除此之外…...

网络协议丨HTTPS是什么?
我们都知道HTTP协议,那什么是HTTPS? 我们都知道,HTTP有两个缺点——“明文”和“不安全”仅凭 HTTP 自身是无力解决的,需要引入新的 HTTPS 协议。 由于 HTTP 天生“明文”的特点,整个传输过程完全透明,任…...
Anaconda常用命令总结,anaconda、conda、miniconda的关系
Anaconda、conda、miniconda的关系 Anaconda Anaconda 是一个用于数据科学,机器学习和深度学习的开源软件包管理系统,其中包括了许多流行的 Python 包和工具Anaconda主要用于科学计算和数据分析。 conda Conda 是 Anaconda 中的包管理器,…...

【蓝桥杯入门到入土】最基础的数组你真的掌握了吗?
文章目录一:数组理论基础二:数组知识点总结三:数组这种数据结构的优点和缺点是什么?四:实战解题1. 移除元素暴力解法双指针法2.有序数组的平方暴力解法双指针法最后说一句一:数组理论基础 首先要知道数组在…...
)
Java Set系列集合(Collections集合工具类、可变参数)
目录Set系列集系概述HashSet集合元素无序的底层原理:哈希表HashSet集合元素去重复的底层原理LinkedHashSet有序实现原理TreeSetCollection集合总结可变参数Collections集合工具类Set系列集系概述 Set系列集合特点 无序:存取顺序不一致不重复࿱…...

chromium构建原生AS项目-记录1
构建的chromium版本:待补充重要说明:so文件加载的过程文件:base_java.jar包文件路径:org.chromium.base.library_loader.LibraryLoader方法:loadAlreadyLocked(Context context)line166 :Native…...
Mybatis-Plus 开发提速器:mybatis-plus-generator-ui
Mybatis-Plus 开发提速器:mybatis-plus-generator-ui 1.简介 github地址 : https://github.com/davidfantasy/mybatis-plus-generator-ui 提供交互式的Web UI用于生成兼容mybatis-plus框架的相关功能代码,包括Entity,Mapper,Mapper.xml,Se…...

李迟2023年02月工作生活总结
本文为 2023 年 2 月工作生活总结。 研发编码 Linux Go 某工程使用到一些数据的统计,为方便,使用 map 存储数量,由于其是无序的,输出的列表顺序不固定,将其和历史版本对比不方便,所以需要将 key 排序再输…...

【Python百日进阶-Web开发-Vue3】Day542 - Vue3 商城后台 02:Windi CSS 与 Vue Router4
文章目录 一、WindiCSS 初始1.1 WindiCSS 是什么?1.2 为什么选择 Windi CSS?1.3. 基础用法1.4 集成二、简单按钮2.1 设置背景色2.2 设置字体颜色和上下左右padding2.3 设置圆角2.4 鼠标悬浮,颜色加深2.5 鼠标划入动画2.6 设置阴影2.7 @apply 抽离class代码到 style 块中三、…...
Jupyter Lab | “丢下R,一起来快乐地糟蹋服务器!”
写作前面 工具永远只是为了帮助自己提升工作效率 —— 沃兹基硕得 所以说,为什么要使用jupyterlab呢?当然是因为基于服务器来处理数据就可以使劲造了,而且深切地感觉到,“R这玩意儿是人用的吗”。 jupyter-lab | mamba安装以及…...
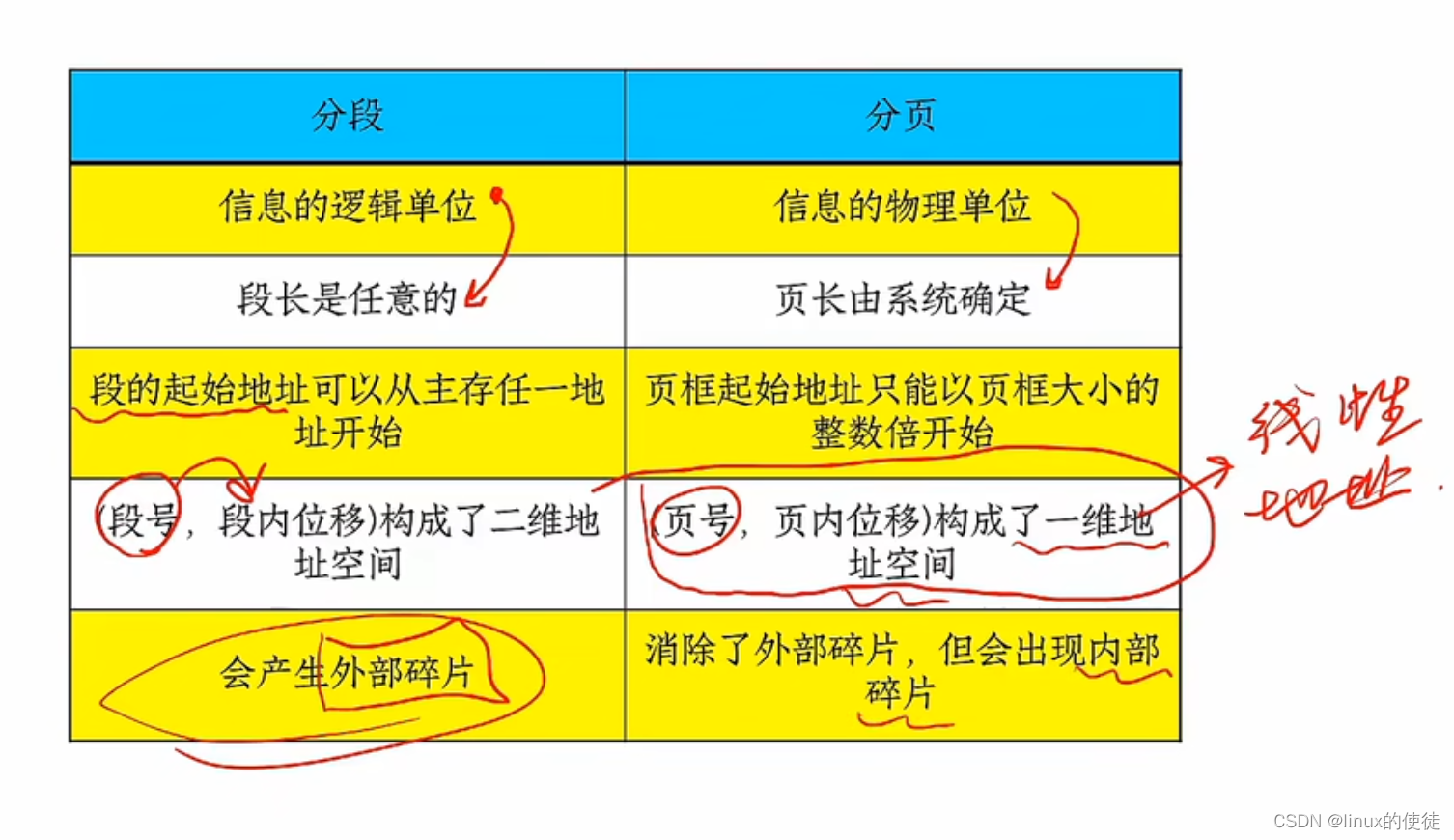
分页与分段
前面我们分析了虚拟地址和物理地址 我们这里进行一个简单的分析 这个是程序运行时的地址映射 那么这些碎片,我们现在的操作系统究竟如何处理呢? 我们再引入一个实际问题 我们如何把右边的进程p塞入左边的内存空间里面 有一种方法将p5kill掉ÿ…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...

用鸿蒙HarmonyOS5实现中国象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的中国象棋小游戏的实现代码。这个实现使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chinesechess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├──…...

【堆垛策略】设计方法
堆垛策略的设计是积木堆叠系统的核心,直接影响堆叠的稳定性、效率和容错能力。以下是分层次的堆垛策略设计方法,涵盖基础规则、优化算法和容错机制: 1. 基础堆垛规则 (1) 物理稳定性优先 重心原则: 大尺寸/重量积木在下…...
