电子技术——CMOS-AB类输出阶
电子技术——CMOS-AB类输出阶

本节我们研究CMOS-AB类输出阶。
经典配置
下图展示了一个经典的CMOS-AB类输出阶:
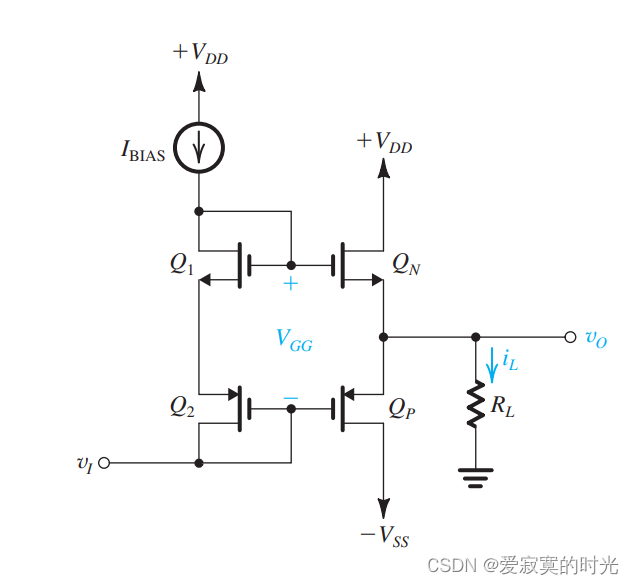
这个很像BJT+二极管偏置版本的AB类输出阶,在这里二极管偏置变成了 Q1Q_1Q1 和 Q2Q_2Q2 偏置。不想BJT的情况,这里 QNQ_NQN 无栅极电流,因此偏置电流 III 完全流过 Q1Q_1Q1 和 Q2Q_2Q2 ,偏置电压 VGGV_{GG}VGG 是一个和负载电流无关的常量。
我们知道:
ID1=I=12kn′(W/L)1(VGS1−Vtn)2I_{D1} = I = \frac{1}{2}k_n'(W/L)_1(V_{GS1} - V_{tn})^2 ID1=I=21kn′(W/L)1(VGS1−Vtn)2
ID2=I=12kp′(W/L)2(VSG2−∣Vtp∣)2I_{D2}= I = \frac{1}{2}k_p'(W/L)_2(V_{SG2} - |V_{tp}|)^2 ID2=I=21kp′(W/L)2(VSG2−∣Vtp∣)2
上述两个式子能够导出:
VGG=VGS1+VSG2=Vtn+∣Vtp∣+2I(1kn′(W/L)1+1kp′(W/L)2)V_{GG} = V_{GS1} + V_{SG2} = V_{tn} + |V_{tp}| + \sqrt{2I} (\frac{1}{\sqrt{k_n'(W/L)_1}} + \frac{1}{\sqrt{k_p'(W/L)_2}}) VGG=VGS1+VSG2=Vtn+∣Vtp∣+2I(kn′(W/L)11+kp′(W/L)21)
同样假设此时处在调平电压 vO=0v_O = 0vO=0 的情况下:
VGG=VGSN+VSGP=Vtn+∣Vtp∣+2IQ(1kn′(W/L)n+1kp′(W/L)p)V_{GG} = V_{GSN} + V_{SGP} = V_{tn} + |V_{tp}| + \sqrt{2I_Q} (\frac{1}{\sqrt{k_n'(W/L)_n}} + \frac{1}{\sqrt{k_p'(W/L)_p}}) VGG=VGSN+VSGP=Vtn+∣Vtp∣+2IQ(kn′(W/L)n1+kp′(W/L)p1)
联立能够导出:
IQ=I[1/kn′(W/L)1+1/kp′(W/L)21/kn′(W/L)n+1/kp′(W/L)p]2I_Q = I [\frac{1 / \sqrt{k_n'(W/L)_1} + 1 / \sqrt{k_p'(W/L)_2}}{1 / \sqrt{k_n'(W/L)_n} + 1 / \sqrt{k_p'(W/L)_p}}]^2 IQ=I[1/kn′(W/L)n+1/kp′(W/L)p1/kn′(W/L)1+1/kp′(W/L)2]2
这表明偏置电流 IQI_QIQ 和电流源 III 的关系只和MOS管的宽长比有关,对于完全匹配的MOS,即 kp′(W/L)2=kn′(W/L)1k_p'(W/L)_2 = k_n'(W/L)_1kp′(W/L)2=kn′(W/L)1 和 kp′(W/L)p=kn′(W/L)nk_p'(W/L)_p = k_n'(W/L)_nkp′(W/L)p=kn′(W/L)n 有:
IQ=I(W/L)n(W/L)1I_Q = I\frac{(W/L)_n}{(W/L)_1} IQ=I(W/L)1(W/L)n
这个方法存在一个缺点,就是限制输出电压的压摆范围,我们假设电流源的压降为 VVV ,我们有:
vO=VDD−V−vGSNv_O = V_{DD} - V - v_{GSN} vO=VDD−V−vGSN
则最大输出电压是当电流源保持最小压降的时候:
vOmax=VDD−Vmin−vGSNv_{Omax} = V_{DD} - V_{min} - v_{GSN} vOmax=VDD−Vmin−vGSN
当 vOv_OvO 达到最大值的时候,此时 iLi_LiL 达到最大值,所有的负载电流都由 QNQ_NQN 提供,此时 vGSNv_{GSN}vGSN 也达到最大值。
vOmax=VDD−Vmin−Vtn−VOVNv_{Omax} = V_{DD} - V_{min} - V_{tn} - V_{OVN} vOmax=VDD−Vmin−Vtn−VOVN
这里的 VOVNV_{OVN}VOVN 是当 QNQ_NQN 通过最大电流 iLi_LiL 时候的过驱动电压。
同样的对于负半周期的最小输出电压为:
vOmin=−VSS+Vmin′+∣Vtp∣+∣vOVP∣v_{Omin} = -V_{SS} + V'_{min} + |V_{tp}| + |v_{OVP}| vOmin=−VSS+Vmin′+∣Vtp∣+∣vOVP∣
不同的是这里的 Vmin′V'_{min}Vmin′ 指的是信号源 vIv_IvI 对 −VSS-V_{SS}−VSS 的最小压降。
我们发现,MOS推挽结构的压摆范围主要收到 VOVNV_{OVN}VOVN 和 ∣vOVP∣|v_{OVP}|∣vOVP∣ 限制,因此最大负载电流越大,压摆范围就越小。因为BJT的压降基本保持在 0.7V0.7V0.7V 左右,因此不受到这个因素的影响,而对于MOS来说,过驱动电压的范围通常变化比较大,我们可以控制MOS的宽长比来限制过驱动电压的最大值,但是对于大型MOS器件来说是不实际的。
使用共源晶体管的另一种替代方案
下面是使用共源晶体管的一种MOS推挽方案:
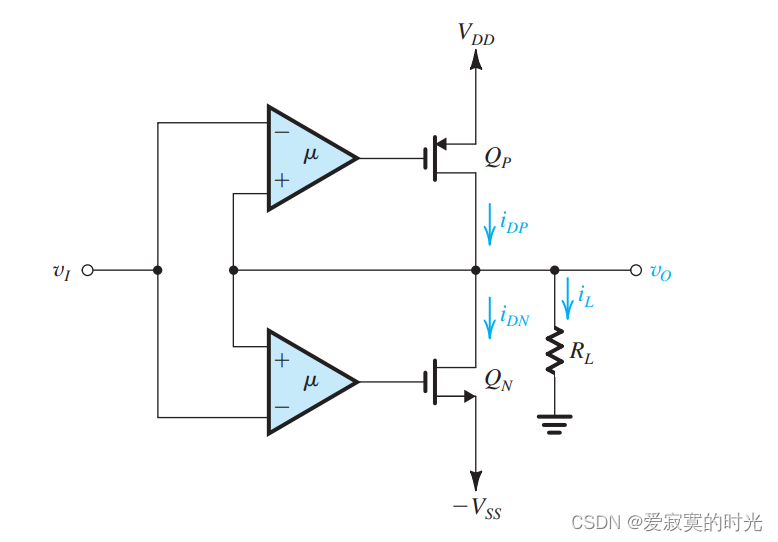
上图中,两个推挽MOS管是共源配置,输入端由两个运算放大器提供驱动,运放和输出电压形成负反馈,根据运放虚短的原理,我们知道 vO≃vIv_O \simeq v_IvO≃vI ,因此我们称运放为 误差放大器 。
为了说明上图中是负反馈,我们假设当 vOv_OvO 升高的时候,此时 QPQ_PQP 的栅极电压升高, iDPi_{DP}iDP 减小,而 QNQ_NQN 的栅极电压升高, iDNi_{DN}iDN 增大,那么 iLi_LiL 就要减小,导致 vOv_OvO 减小。因此上图中是负反馈。
并且,我们之前学过,上图是一个串联-并联结构,是一个典型的电压放大器,增益为单位增益,具有较大的输入阻抗和较小的输出阻抗。
为了计算小信号的输出阻抗,我们分别考虑电路的一半,对于上半部分计算 RoutpR_{outp}Routp 下半部分计算 RoutnR_{outn}Routn 那么整体的输出阻抗为:
Rout=Routp∣∣RoutnR_{out} = R_{outp} || R_{outn} Rout=Routp∣∣Routn
下图是上半部分电路:
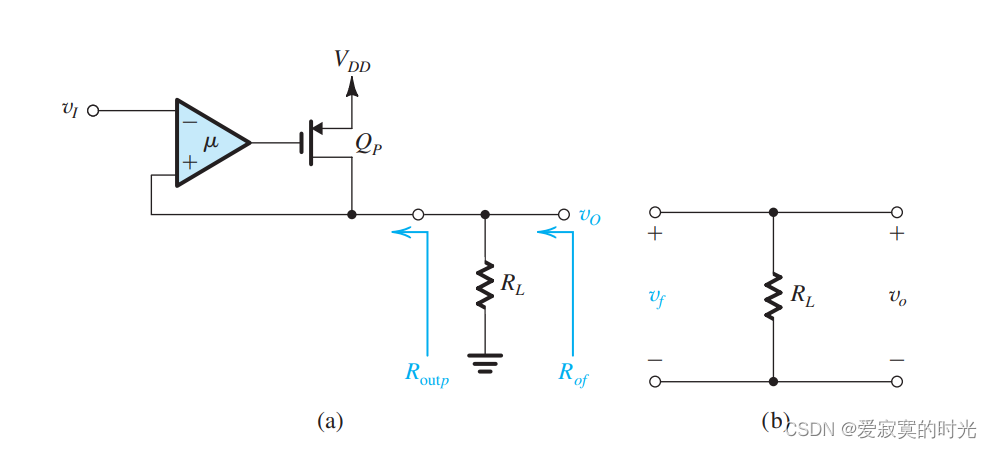
其中反馈网络为图 (b) 反馈因子为 β=1\beta = 1β=1 。
使用系统分析法分析开环增益,如图:

然后施加测试源 viv_ivi 计算输出 vov_ovo 我们知道:
A=μgmp(rop∣∣RL)A = \mu g_{mp} (r_{op} || R_L) A=μgmp(rop∣∣RL)
其中 gmpg_{mp}gmp 和 ropr_{op}rop 是 QPQ_PQP 的小信号参数,可由 QPQ_PQP 的电流决定,开环输出阻抗为:
Ro=RL∣∣ropR_o = R_L || r_{op} Ro=RL∣∣rop
则负反馈等效输出阻抗为:
Rof=Ro1+Aβ=(rop∣∣RL)1+μgmp(rop∣∣RL)R_{of} = \frac{R_o}{1 + A\beta} = \frac{(r_{op} || R_L)}{1 + \mu g_{mp} (r_{op} || R_L)} Rof=1+AβRo=1+μgmp(rop∣∣RL)(rop∣∣RL)
那么输出阻抗为:
Routp=1/(1Rof−1RL)=rop∣∣1μgmp≃1μgmpR_{outp} = 1 / (\frac{1}{R_{of}} - \frac{1}{R_L}) = r_{op} || \frac{1}{\mu g_{mp}} \simeq \frac{1}{\mu g_{mp}} Routp=1/(Rof1−RL1)=rop∣∣μgmp1≃μgmp1
可见输出阻抗足够小,对于下半部分电路同样的:
Routn≃1μgmnR_{outn} \simeq \frac{1}{\mu g_{mn}} Routn≃μgmn1
则总输出阻抗为:
Rout≃1μ(gmp+gmn)R_{out} \simeq \frac{1}{\mu (g_{mp} + g_{mn})} Rout≃μ(gmp+gmn)1
接下来,我们推导其传导特性,我们使用下面的电路图:
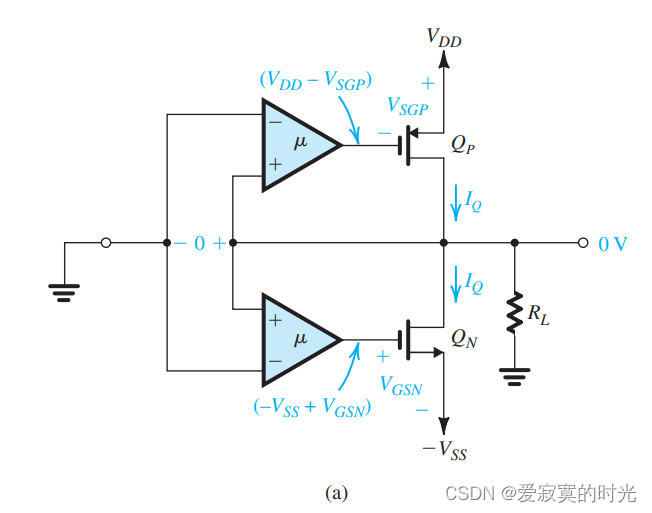
首先我们考虑其静态点参数,对于 vI=0v_I = 0vI=0 此时 vO=0v_O = 0vO=0 。此时偏置电流 IQI_QIQ 将完全由电路的静态点误差决定:
IQ=12kp′(W/L)pVOV2=12kn′(W/L)nVOV2I_Q = \frac{1}{2} k_p'(W/L)_p V_{OV}^2 = \frac{1}{2} k_n'(W/L)_n V_{OV}^2 IQ=21kp′(W/L)pVOV2=21kn′(W/L)nVOV2
这里的 VOV2V_{OV}^2VOV2 是静态点的过驱动电压,若两个MOS完全匹配:
IQ=12kVOV2I_Q = \frac{1}{2}k V_{OV}^2 IQ=21kVOV2
接下来考虑应用输入信号电压 vIv_IvI ,如下图:
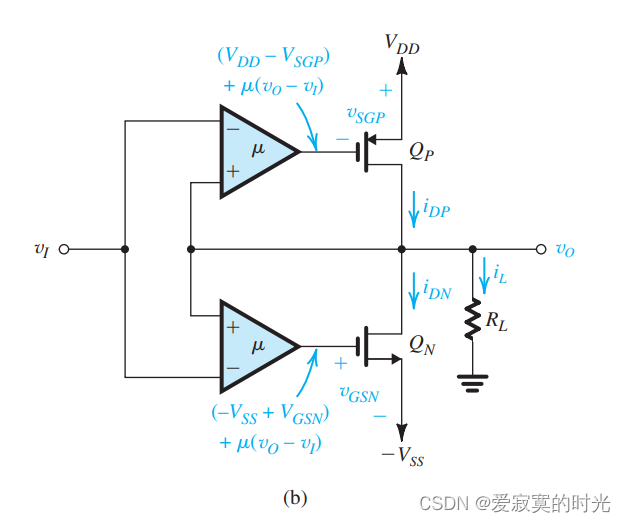
此时两个误差放大器的输出增加了输入输出误差 μ(vO−vI)\mu(v_O - v_I)μ(vO−vI) ,则此时:
iDP=12k[VOV−μ(vO−vI)]2=IQ(1−μvO−vIVOV)2i_{DP} = \frac{1}{2}k[V_{OV} - \mu(v_O - v_I)]^2 = I_Q (1 - \mu\frac{v_O - v_I}{V_{OV}})^2 iDP=21k[VOV−μ(vO−vI)]2=IQ(1−μVOVvO−vI)2
iDN=IQ(1+μvO−vIVOV)2i_{DN} =I_Q (1 + \mu\frac{v_O - v_I}{V_{OV}})^2 iDN=IQ(1+μVOVvO−vI)2
则信号电流为:
iL=iDP−iDNi_L = i_{DP} - i_{DN} iL=iDP−iDN
带入 iL=vO/RLi_L = v_O / R_LiL=vO/RL 得到:
vO=vI1+VOV4μIQRLv_O = \frac{v_I}{1 + \frac{V_{OV}}{4 \mu I_Q R_L}} vO=1+4μIQRLVOVvI
又因为 VOV4μIQRL≪1\frac{V_{OV}}{4 \mu I_Q R_L} \ll 14μIQRLVOV≪1 近似为:
vO≃vI(1−VOV4μIQRL)v_O \simeq v_I(1 - \frac{V_{OV}}{4 \mu I_Q R_L}) vO≃vI(1−4μIQRLVOV)
增益误差定义为:
E≡vOvI−1=−VOV4μIQRLE \equiv \frac{v_O}{v_I} - 1 = -\frac{V_{OV}}{4 \mu I_Q R_L} E≡vIvO−1=−4μIQRLVOV
因为在静态点处 gmp=gmn=gm=2IQVOVg_{mp} = g_{mn} = g_m = \frac{2I_Q}{V_{OV}}gmp=gmn=gm=VOV2IQ 也可以表示为:
E=−12μgmRLE = -\frac{1}{2 \mu g_m R_L} E=−2μgmRL1
因此选择较大的 μ\muμ 可以降低输入输出误差,以及降低输出阻抗。然而较大的 μ\muμ 会让 IQI_QIQ 过于依赖运放的输入偏移电压。一般,通常让 μ\muμ 在5到10的范围内。同时,较大的 IQI_QIQ 会减小交越失真,输出阻抗和误差,但是会引起较大的静态耗散功率。
书中没给出 IQI_QIQ 的计算方法,故在此给出,假设静态输出电压为 VOV_OVO ,那么有:
IQ=12kp(VDD−μVO−∣Vtp∣)2I_Q = \frac{1}{2}k_p(V_{DD} - \mu V_O - |V_{tp}|)^2 IQ=21kp(VDD−μVO−∣Vtp∣)2
IQ=12kn(VSS+μVO−Vtn)2I_Q = \frac{1}{2}k_n(V_{SS} + \mu V_O - V_{tn})^2 IQ=21kn(VSS+μVO−Vtn)2
两个式子联立可以解得 IQI_QIQ 和 VOV_OVO 的值:
VO=kp(VDD−∣Vtp∣)−kn(VSS−Vtn)μ(kp+kn)V_O = \frac{\sqrt{k_p}(V_{DD} - |V_{tp}|) - \sqrt{k_n}(V_{SS} - V_{tn})}{\mu (\sqrt{k_p} + \sqrt{k_n})} VO=μ(kp+kn)kp(VDD−∣Vtp∣)−kn(VSS−Vtn)
我们发现 IQI_QIQ 理论上是与 μ\muμ 无关量,调整MOS参数即可调整 IQI_QIQ 。
相关文章:

电子技术——CMOS-AB类输出阶
电子技术——CMOS-AB类输出阶 本节我们研究CMOS-AB类输出阶。 经典配置 下图展示了一个经典的CMOS-AB类输出阶: 这个很像BJT二极管偏置版本的AB类输出阶,在这里二极管偏置变成了 Q1Q_1Q1 和 Q2Q_2Q2 偏置。不想BJT的情况,这里 QNQ_NQN…...

2023王道考研数据结构笔记第二章线性表
第二章 线性表 2.1 线性表的定义 2.1.1 线性表的基本概念 线性表是具有相同数据类型的n(n>0)个数据元素的有限序列,其中n为表长,当n0时线性表是一个空表。若用L命名线性表,则其一般表示为: L(a1,a2,...,ai,ai1,...,an)L(a_1…...
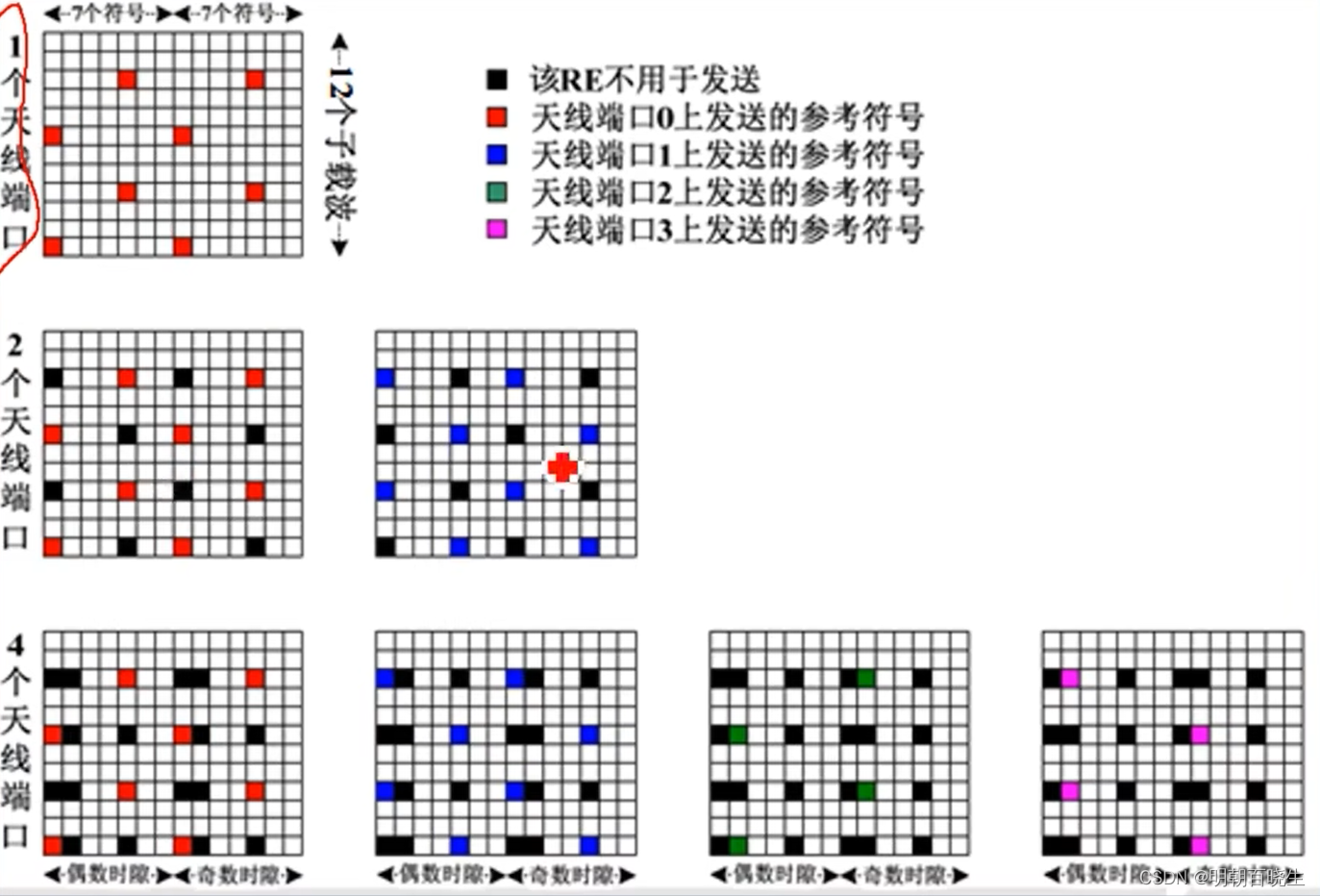
[chapter 11][NR Physical Layer][Layer Mapping]
前言:这里参考Curious Being系列 ,简单介绍一下NR 5G 物理层核心技术层映射.我们主要讲了一下what is layer Mapping, why need layer Mapping, how layer Mapping 参考文档:3GPP 38.211- 6.3.1.3 Layer mapping《5G NR Physical Layer | Cha…...

什么是工业物联网(IIoT)?
什么是工业物联网(IIoT)?工业物联网(IIoT) 被定义为一组设备和应用,允许大企业创建从核心到边缘的端到端连接环境。其还包括传统的物理基础设施,如集装箱和物流卡车,以收集数据,对事件做出反应,并在智能设备的帮助下做…...
「TCG 规范解读」PC 平台相关规范(4)
可信计算组织(Ttrusted Computing Group,TCG)是一个非盈利的工业标准组织,它的宗旨是加强在相异计算机平台上的计算环境的安全性。TCG于2003年春成立,并采纳了由可信计算平台联盟(the Trusted Computing Platform Alli…...

CSS背景属性之颜色渐变
颜色渐变 颜色渐变其实在网页设计中并不是特别常见, 但也不可避免的会出现导航栏是渐变色这种情况或者别的不是单一颜色的情况, 例如:这样的设计解决方案并不是只可以使用颜色渐变,我们可以使用两个div拼接,将文字放…...
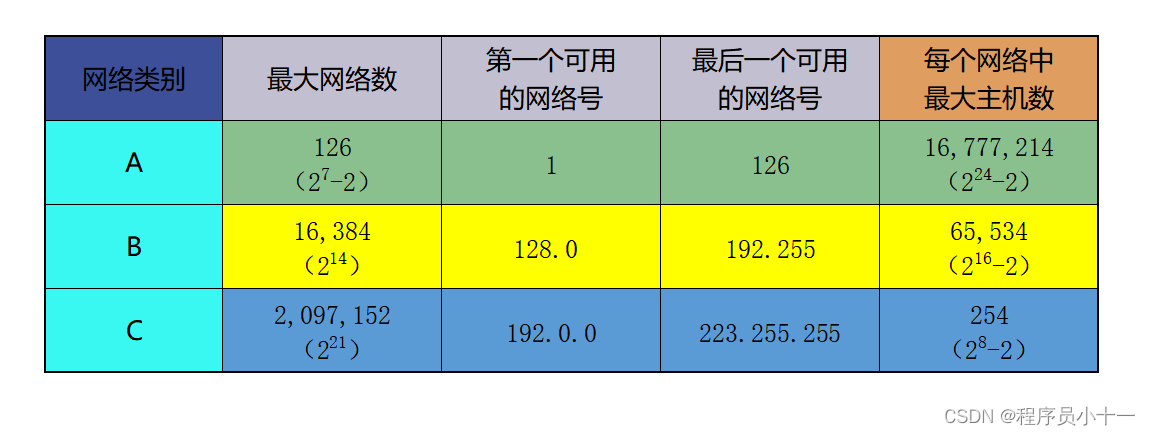
IPv4地址细讲
文章目录一、IPv4地址简介二、IPv4地址的表示方法点分十进制记法三、IP地址的分类四、特殊IPv4地址:全 “0” 和全 “1”五、常用的三类IP地址使用范围六、五类IP地址的范围一、IPv4地址简介 IPv4地址分5类,每一类地址都由固定长度的字段组成࿱…...

sql语句中exists用法详解
文章目录一、语法说明exists:not exists:二、常用示例说明1.查询a表在b表中存在数据2.查询a表在b表中不存在数据3.查询时间最新记录4.exists替代distinct剔除重复数据总结一、语法说明 exists: 括号内子查询sql语句返回结果不为空ÿ…...

思迅软件端口不通导致软件和软锁报错的问题
一、端口不通导致软件和软锁报错的问题 问题说明:打开软件提示到:xxx.xxx.xxx.xxx失败! 处理步骤1: 假设软锁服务器IP为192.168.0.1,分别在服务器本机和客户端电脑测试软锁服务: 在服务器的浏览器中访问地址: http:/…...
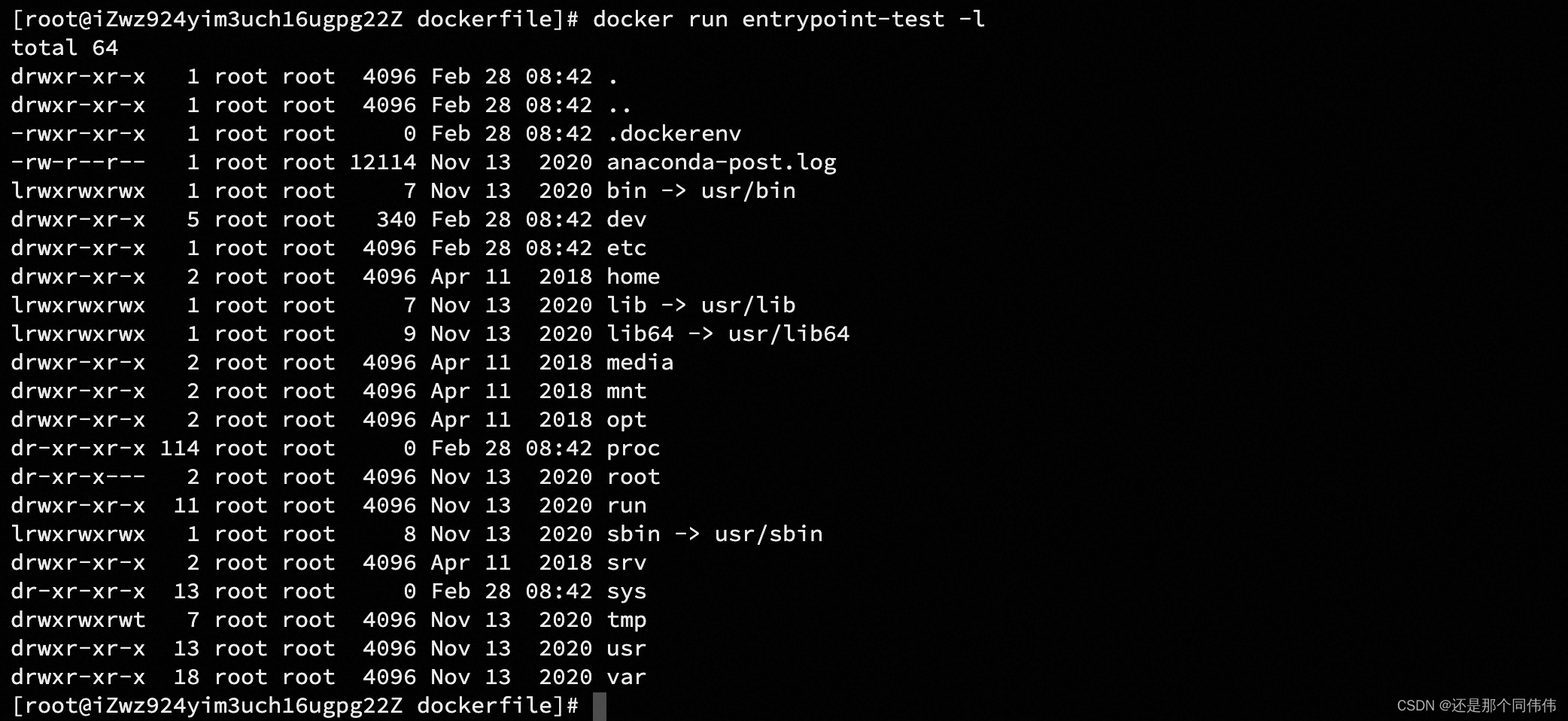
Docker之路(7.DockerFile文件编写、DockerFile 指令解释、CMD与ENTRYPOINT的区别)
1.DockerFile介绍 dockerfile 是用来构建docker镜像的文件!命令参数脚本! 构建步骤: 编写一个dockerfile文件docker build构建成为一个镜像docker run 运行镜像docker push发布镜像(DockerHub、阿里云镜像仓库) 2.Dock…...

[软件测试]如何使用Eclipse导入项目并打开
🧑🎓个人介绍:大二软件生,现学JAVA、Linux、MySQL、算法 💻博客主页:渡过晚枫渡过晚枫 👓系列专栏:[编程神域 C语言],[java/初学者],[蓝桥杯] Ὅ…...

emplace_back与push_back异同
vector的emplace_back与push_back 文章目录vector的emplace_back与push_back前言1.区别总览2.push_back支持右值引用不支持传入多个构造参数总是会进行拷贝构造3.emplace_backemplace_back可以接受多个构造参数支持原地构造前言 在vector中,通过push_back与emplace_…...
【C语言航路】第十五站:程序环境和预处理
目录 一、程序的翻译环境和执行环境 二、编译和链接 1.翻译环境 2.编译本身也分为几个阶段 3.运行环境 三、预处理 1.预定义符号 2.#define 1.#define定义标识符 2.#define定义宏 3.#define 替换规则 4.#和## 5.带副作用的宏参数 6.宏和函数的对比 7.命名约定 …...
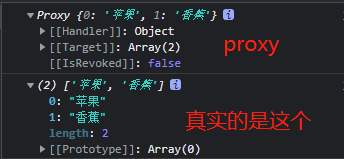
Vue3 - 获取 Proxy 对象代理中包裹的 “真实数据“,解决对象或数组打印后是 Proxy 对象无法拿到原始数据的问题(提供 2 种详细解决方案)
前言 在 Vue3 中很多数据都被 Proxy 代理对象 “包裹”(无法拿到其真正的原始数据),另外就是请求回来的数据,例如通过 res.data.data 拿到了一个数组对象格式的数据。但是这个数据被 Proxy 包裹,你根本拿不到值无法进行处理。 本文实现了 Vue3 取到被 proxy 对象包裹的原始…...

ESP32设备驱动-ML8511紫外线传感器驱动
ML8511紫外线传感器驱动 1、ML8511介绍 ML8511 是一款紫外线传感器,适用于室内或室外获取紫外线强度。 ML8511 配备了一个内部放大器,可根据紫外线强度将光电流转换为电压。 这种独特的功能提供了与 ADC 等外部电路的简单接口。 在掉电模式下,典型的待机电流为 0.1 μ \mu…...

SC12B触摸感应芯片评测方案(1)
MM32F0160SC12B Touch Application Evaluation 文章目录MM32F0160SC12B Touch Application EvaluationIntroduction & RequirementHardwareSC12B & SC12B Sample Demo boardMini-F0160 boardSoftwareMCU Software - MM32F0160PC Tool - FreeMASTERSummaryIntroduction …...
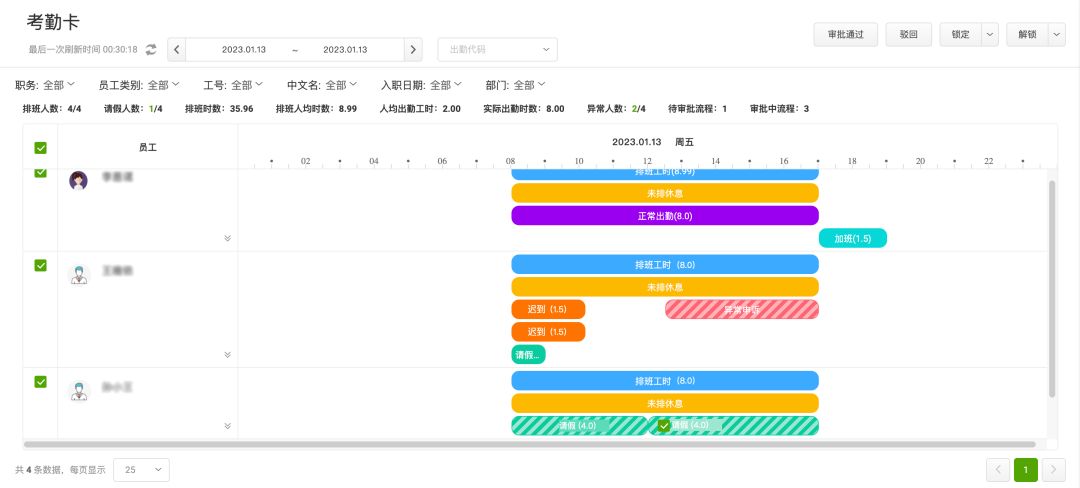
企业如何实现精细化人员管理?五大业务场景值得关注
近年来,随着大数据、人工智能和云计算等信息技术不断升级与渗透,处在数字化变革的劳动力密集型企业希望利用更加智能化的劳动力管理软件,帮助企业实现规范化的管理。 面对企业劳动力管理理念的变化,以及数字化转型的发展渗透&…...
C/C++每日一练(20230301)
目录 1. 冒泡排序法排序 ★ 2. 有效的数独 ★★ 3. 不同的二叉搜索树 II ★★ 附录 二叉搜索树 1. 冒泡排序法排序 输入n(1≤n≤10)个整数,用冒泡排序法对其从小到大排序,共进行n-1趟,要求输出每一趟的排序情…...
Vue项目中components组件的使用笔记
目录 前言 一、components和component的区别? 二、components使用的步骤 1.创建组件vue文件 2.引入组件 3.注册组件 4.应用组件 总结 前言 本文章,只是初步了解记录components的使用步骤。 一、components和component的区别? compo…...

2023软件测试行情不行了?
一、2023年软件测试行业的现状 2020年开年,一不小心,【新冠】黑天鹅从头上飘过,持续影响全国乃至全球的经济,软件行业公司也迎来了不少的冲击,那么一个值得打算入行软件测试行业,或者已经在软件测试行业耕耘…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...

《Offer来了:Java面试核心知识点精讲》大纲
文章目录 一、《Offer来了:Java面试核心知识点精讲》的典型大纲框架Java基础并发编程JVM原理数据库与缓存分布式架构系统设计二、《Offer来了:Java面试核心知识点精讲(原理篇)》技术文章大纲核心主题:Java基础原理与面试高频考点Java虚拟机(JVM)原理Java并发编程原理Jav…...
