二分算法题
文章目录
- 一、在排序数组中查找数字
- 二、0~n-1中缺失的数字
- 三、旋转数组的最小数字
- 四、二维数组中的查找
一、在排序数组中查找数字
题目传送门
法一:暴力解
直接遍历然后计数
法二:二分法求边界
看到关键字排序数组、有序数组,一定要想到二分的方法,效率高,思路也比较简单
思路:使用二分法、找数组的左边界(left)和右边界(right),最后目标数字个数就是right-left+1
对于二分法,我们可以分别求左边界和右边界,也可以二分求左边界之后接着遍历计数,两种情况对应在真实场景下连续相等的数据一般有多长。如果经常出现很长一串连续相等的数据,就用二分法求右边界,否则容易使算法退化到O(N)。PS: 在C ++11 标准中,nums.size()的时间复杂度是Constant常数级,O(1)
class Solution {
public:int search(vector<int>& nums, int target) {int res=0;int idx=getFirstIndex(nums,target);if(idx==-1) return res;for(int i=idx;i<nums.size()&&nums[i]==target;i++){res++;}return res;}int getFirstIndex(vector<int> & nums,int target){int left=0;int right=nums.size()-1;int res=-1;while(left<=right){int mid=(left+right)/2;if(nums[mid]>target){right=mid-1;}else if(nums[mid]<target){left=mid+1;}else{res=mid;right=mid-1;} }return res;}
};
标准解法:
class Solution {
public:int binarySearch(vector<int>& nums, int target, bool lower) {int left = 0, right = (int)nums.size() - 1, ans = (int)nums.size();while (left <= right) {int mid = (left + right) / 2;if (nums[mid] > target || (lower && nums[mid] >= target)) {right = mid - 1;ans = mid;} else {left = mid + 1;}}return ans;}int search(vector<int>& nums, int target) {int leftIdx = binarySearch(nums, target, true);int rightIdx = binarySearch(nums, target, false) - 1;if (leftIdx <= rightIdx && rightIdx < nums.size() && nums[leftIdx] == target && nums[rightIdx] == target) {return rightIdx - leftIdx + 1;}return 0;}
};
二、0~n-1中缺失的数字
题目传送门
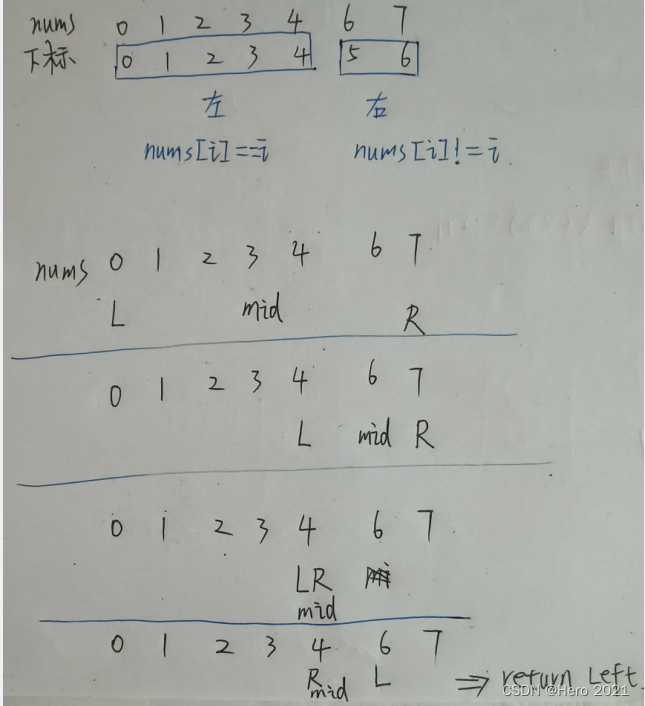
思路:因为有序,所以可以看看下标是否等于数组中的对应元素
初始化: 左边界 left = 0 ,右边界 right = len(nums)−1 ;代表闭区间 [left, right] 。
循环二分: 当 left ≤ right 时循环 (即当闭区间 [left, right] 为空时跳出) ;
1、计算中点 mid = (left + right)//2 ,其中 “//” 为向下取整除法;
2、若 nums[mid] = mid ,说明mid前面的元素肯定都是完整的不少元素所以只需要继续二分右边的数组即可,则 “右子数组的首位元素” 一定在闭区间 [mid+1, right] 中,因此执行 left = mid+1;
3、若 nums[mid] != mid ,说明mid前面的元素就有少的所以只要继续二分左边的数组即可,则 “左子数组的末位元素” 一定在闭区间 [left, mid−1] 中,因此执行 right = mid−1;
4返回值: 跳出时,变量 i 和 j 分别指向 “右子数组的首元素” 和 “左子数组的末元素” 。因此返回 i 即可。
class Solution {
public:int missingNumber(vector<int>& nums) {int left=0,right=nums.size()-1;while(left<=right){int mid=(left+right)/2;if(nums[mid]==mid){left=mid+1;}else{right=mid-1;}}return left;}
};
三、旋转数组的最小数字
题目传送门
题目分析
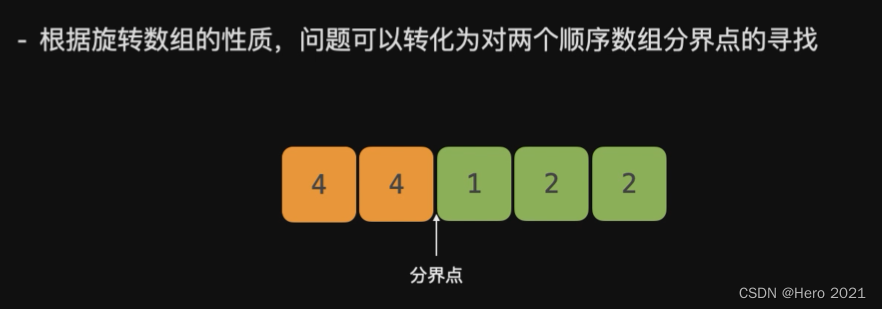
旋转数组:把一个有重复数字的有序数组,末位一部分移动到头部,这就叫做旋转数组。在这里插入图片描述
我们的目标就是找到这个分界点!
法一:暴力
分界点右边的第一个数字就是我们要找的最小数字
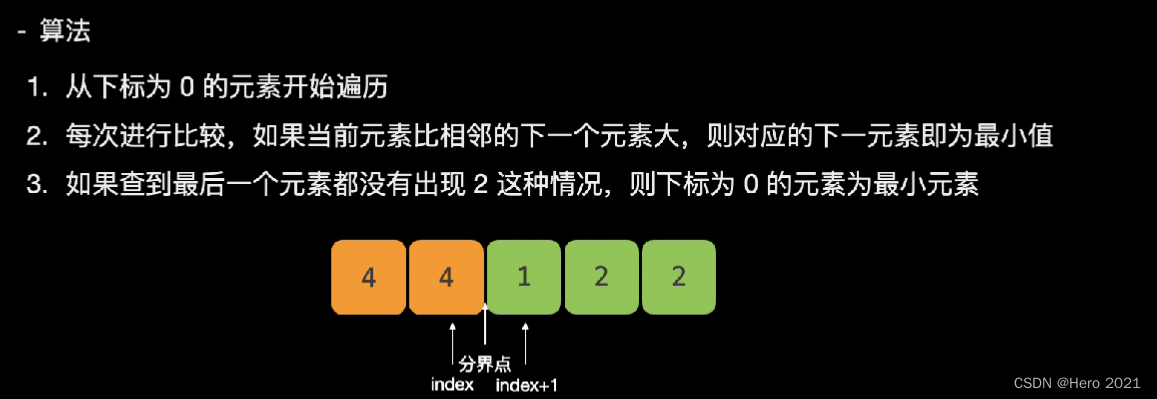
其实可以类比数学中的找极点

class Solution {
public:int minArray(vector<int>& numbers) {// 注意i=0开始,要越界,特殊处理一下,从1开始可以避免for(int i=1;i<numbers.size();i++){if(numbers[i-1]>numbers[i])return numbers[i];}return numbers[0];}
};
法二:二分法
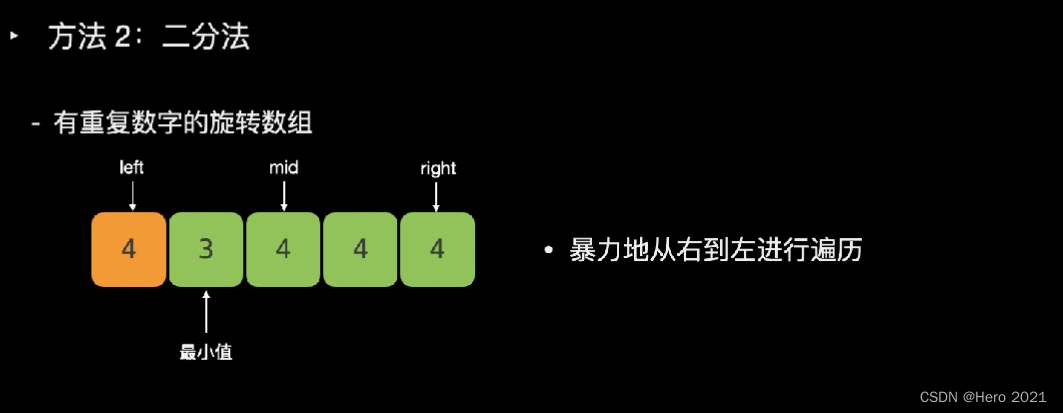
题目说了,可能存在重复的数字
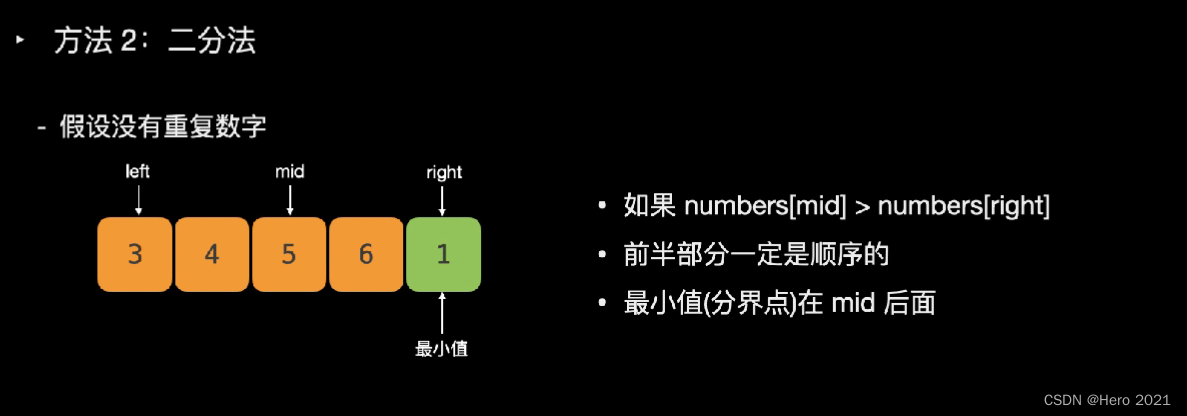

---------------------===

class Solution {
public:int minArray(vector<int>& numbers) {int left=0;int right=numbers.size()-1;if(right==0) return numbers[0];while(left<right){int mid=left+(right-left)/2;if(numbers[mid]>numbers[right])left=mid+1;else if(numbers[mid]<numbers[right])right=mid;elseright--;}return numbers[left];}
};
四、二维数组中的查找
TP
法一:暴力
直接遍历矩阵,判断有没有target
class Solution {
public:bool findNumberIn2DArray(vector<vector<int>>& matrix, int target) {for(auto row: matrix){for(auto e: row){if(e==target)return true;}}return false;}
};
时间复杂度:O(MN)
空间复杂度:O(1)
法二:行二分
对二维数组每一行,进行二分查找
class Solution {
public:bool findNumberIn2DArray(vector<vector<int>>& matrix, int t) {if (matrix.size() == 0 || matrix[0].size() == 0) return false;int n = matrix.size(), m = matrix[0].size();int l = 0, r = 0, mid = 0;for (int i = 0; i < n; i ++) {l = 0;r = m - 1;while (l <= r) {mid = l + (r - l) / 2;if (matrix[i][mid] == t) return true;if (matrix[i][mid] < t) l = mid + 1;if (matrix[i][mid] > t) r = mid - 1;} }return false;}
};
时间复杂度:O(MlogN)
空间复杂度:O(1)
法三:Z字形查找
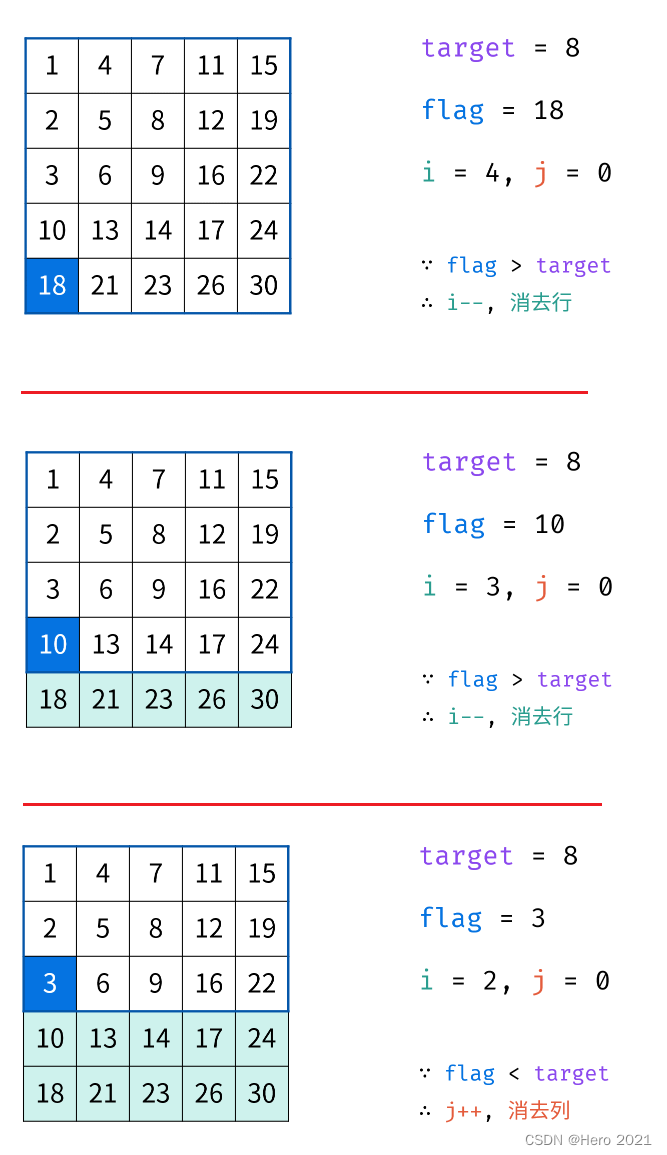
class Solution
{
public:bool findNumberIn2DArray(vector<vector<int>> &matrix, int target){int i = matrix.size() - 1; // 行int j = 0; // 列if (matrix.size() == 0 || matrix[0].size() == 0)return false;while (i >= 0 && j <= matrix[0].size() - 1){if (matrix[i][j] > target)i--;else if (matrix[i][j] < target)j++;elsereturn true;}return false;}
};
时间复杂度:O(M+N)
M,N为矩阵的行数和列数
空间复杂度:O(1)
相关文章:

二分算法题
文章目录一、在排序数组中查找数字二、0~n-1中缺失的数字三、旋转数组的最小数字四、二维数组中的查找一、在排序数组中查找数字 题目传送门 法一:暴力解 直接遍历然后计数 法二:二分法求边界 看到关键字排序数组、有序数组,一定要想到二分…...
Vue+ElementUI+SpringBoot项目配合分页插件快速实现分页(简单暴力)
首先需要在项目中引入Element-UI的组件库,使用以下命令,不会引入的请自行百度。 npm i element-ui -S Element官网地址:https://element.eleme.cn/#/zh-CN/component/changelog 去Element-UI官网组件库找到合适的分页插件,并把他引…...
)
【回眸】牛客网刷刷刷!嵌入式软件中也会遇到的嵌入式硬件,通讯,通讯协议专题(一)
前言 最近继续刷题,看看嵌入式软件还需要了解一些嵌入式硬件中的通讯协议和常用接口协议 比如说SPI CAN I2C 通讯协议专题 1.波特率 波特率 每秒传送的字符数 * 字符位数。串口的工作模式为1个起始位,7个数据位,1个校验位,1个…...
使用Vue展示数据(动态查询)
学习内容来源:视频P4 本篇文章进度接着之前的文章进行续写 精简前后端分离项目搭建 Vue基础容器使用 目录选择组件修改表格组件修改分页组件增加后端接口前端请求数据接口页面初始化请求数据点击页码请求数据选择组件 在官方文档中选择现成的组件,放在页…...

构建数据库测试数据——mysql
建表脚本 -- 建表 CREATE TABLE test_table (id INT(11) NOT NULL AUTO_INCREMENT,varchar_col VARCHAR(50),char_col CHAR(10),text_col TEXT,tinyint_col TINYINT(4),smallint_col SMALLINT(6),mediumint_col MEDIUMINT(9),int_col INT(11),bigint_col BIGINT(20),float_col…...
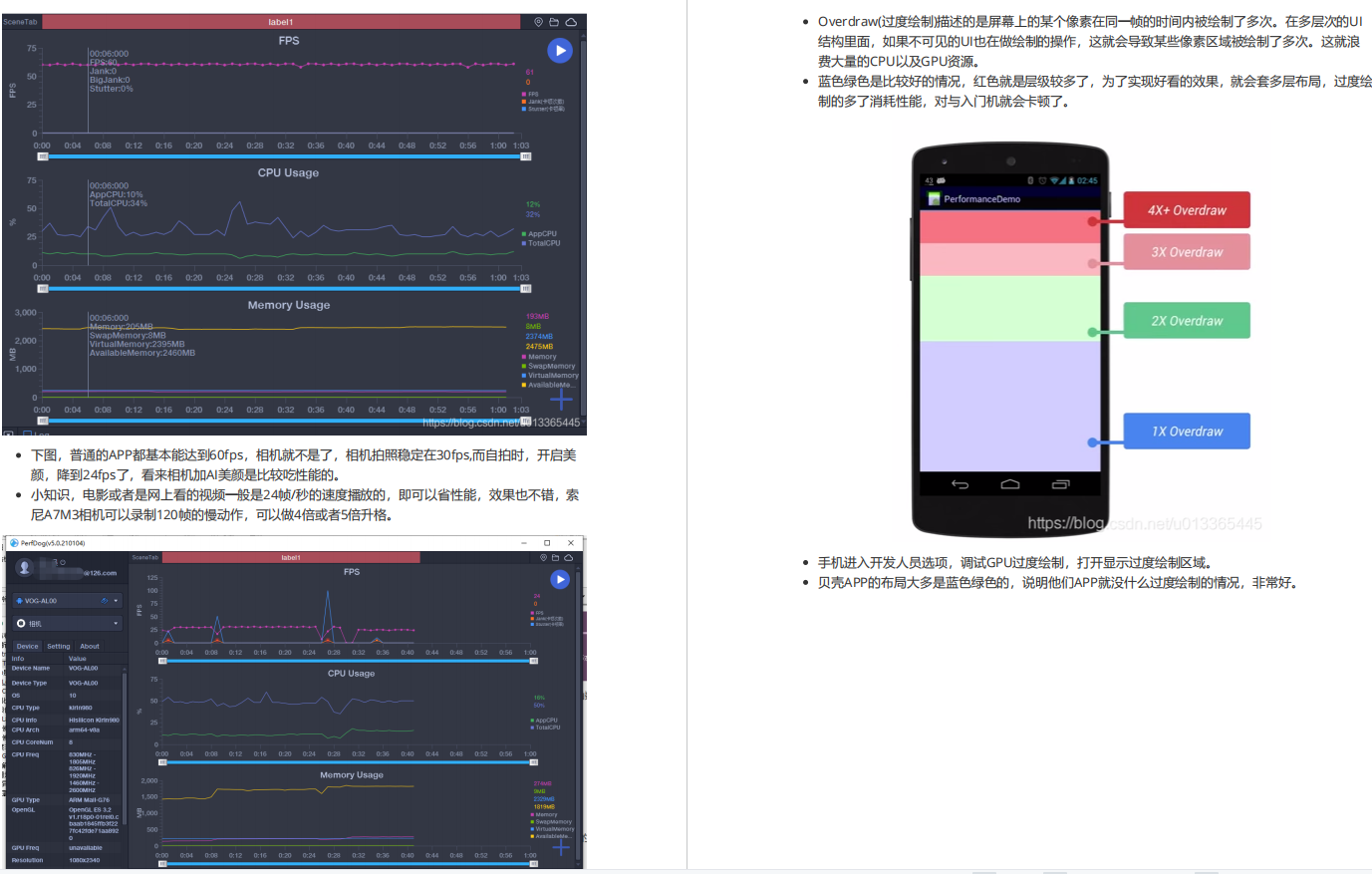
你想要的Android性能优化系列:启动优化 !
App启动优化为什么要做App的启动优化?网页端存在的一个定律叫8秒定律:即指用户访问一个网站时,如果等待打开的时间超过8秒,超过70%的用户将会放弃等待。同样的,移动端也有一个8秒定律:如果一个App的启动时间…...

python3的基础入门3:基本数据类型
基本数据类型 python 中的变量不需要声明。每个变量在使用前都必须赋值,变量赋值以后该变量才会被创建。 在 Python 中,变量就是变量,它没有类型,我们所说的"类型"是变量所指的内存中对象的类型。 等号(&…...
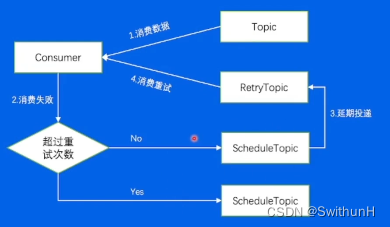
消息队列原理与实战-学习笔记
消息队列:保存消息的一个容器,本质是个队列,但是需要支持高吞吐、高并发、高可用。 1 前世今生 1.1 业界消息队列对比 Kafka:分布式的、分区的、多副本的日志提交服务,在高吞吐场景下发挥较为出色RocketMQ:低延迟、强一致、高性…...

Linux权限相关知识(大量图文展示,及详细操作)
Linux权限相关概念 Linux下有两种用户:一种是超级用户(root)、一种是普通用户。 超级用户:可以在linux系统下做任何事情,不受限制 普通用户:在linux下做有限的事情。 超级用户的命令提示符是“#”…...
Ep_操作系统面试题-什么是协程
协程 是一种 比线程更加轻量级的存 在,一个线程可以拥有多个协程。是一个特殊的 函数 ,这个函数可以在某个地方挂起,并且可以重新在挂起处外继续运行。协程 不是被操作系统内核所管理 , 而完全是由程序所控制(也就是在…...

在C#中使用互斥量解决多线程访问共享资源的冲突问题
在阿里云上对互斥量的概述:互斥量的获取是完全互斥的,即同一时刻,互斥量只能被一个任务获取。而信号量按照起始的计数值的配置,可以存在多个任务获取同一信号量的情况,直到计数值减为0,则后续任务无法再获取…...

JavaEE进阶第六课:SpringBoot配置文件
上篇文章介绍了SpringBoot的创建和使用,这篇文章我们将会介绍SpringBoot配置文件 目录1.配置文件的作用2.配置文件的格式2.1 .properties语法2.1.1.properties的缺点2.2 .yml语法2.2.1优点分析2.2.2配置与读取对象2.2.3配置与读取集合2.2.4补充说明3.设置不同环境的…...
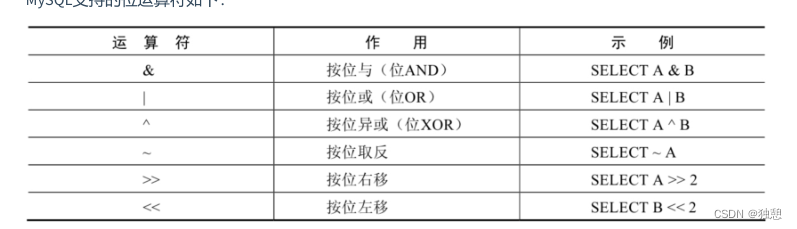
MySQL基础(一)SQL分类、导入、SELECT语句,运算符
目录 MySQL安装以及相关工具 SQL分类 导入数据 最基本的SELECT语句 SELECT FROM 列的别名 去除重复行 着重号 查询常数 描述表结构 过滤数据(重要) 运算符 算数运算符 比较运算符 符号运算符 非符号运算符 逻辑运算符 位运算符 MySQL安…...

反激与正激的区别
之前学习了正激开关电源,但是对于正激和反激一直不是很清楚,网上找了一篇,觉得感觉该可以,以此记录。正激和反激是两种不同的开关电源技术一、正激(1)概述正激式开关电源是指使用正激高频变压器隔离耦合能量…...
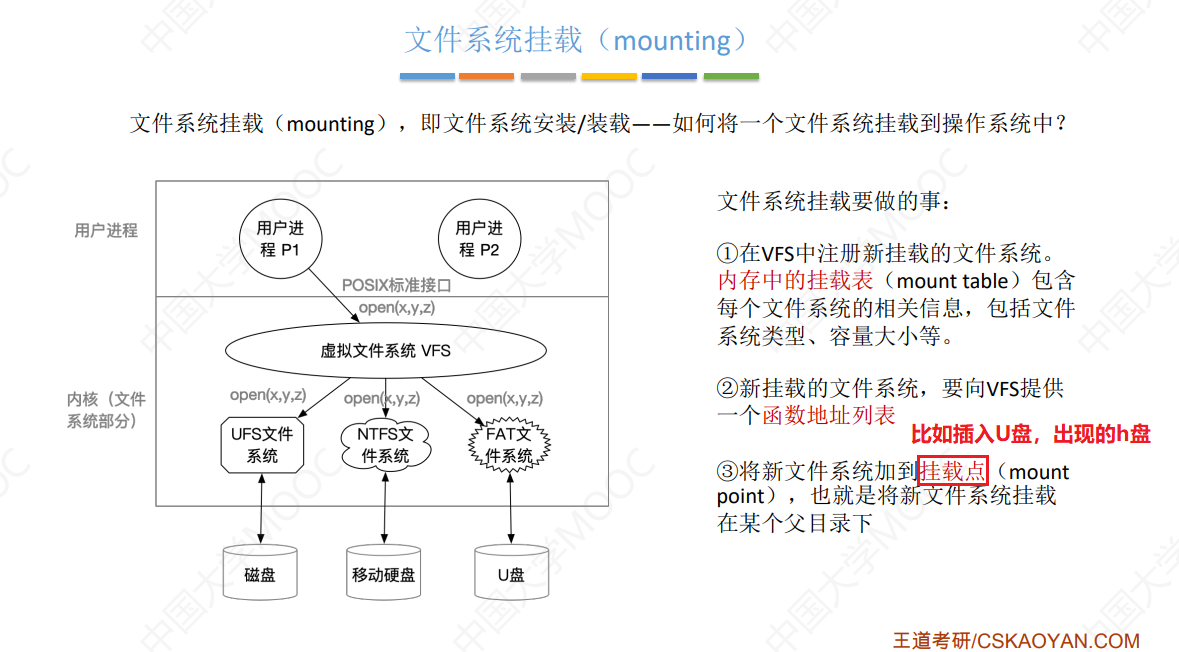
王道操作系统课代表 - 考研计算机 第四章 文件管理 究极精华总结笔记
本篇博客是考研期间学习王道课程 传送门 的笔记,以及一整年里对 操作系统 知识点的理解的总结。希望对新一届的计算机考研人提供帮助!!! 关于对 “文件管理” 章节知识点总结的十分全面,涵括了《操作系统》课程里的全部…...

前端开发规范,你真的了解吗?一起来学习一下前端开发规范,让你的代码高级起来!
代码规范 1 编码风格规范 1.1 使用ES6风格编码源码 定义变量使用let ,定义常量使用const 使用export ,import 模块化 1.2 组件 props 原子化 提供默认值 使用 type 属性校验类型 使用 props 之前先检查该 prop 是否存在 1.3 避免 this.$parent 1.4 谨慎使用 …...
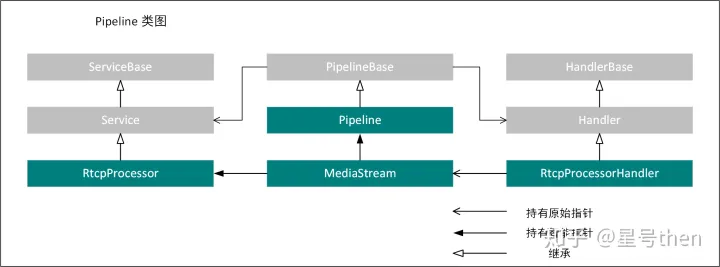
Licode—基于webrtc的SFU/MCU实现
1. webrtc浅析webrtc的前世今生、编译方法、行业应用、最佳实践等技术与产业类的文章在网上卷帙浩繁,重复的内容我不再赘述。对我来讲,webrtc的概念可以有三个角度去解释:(1).一个W3C和IETF制定的标准,约定…...
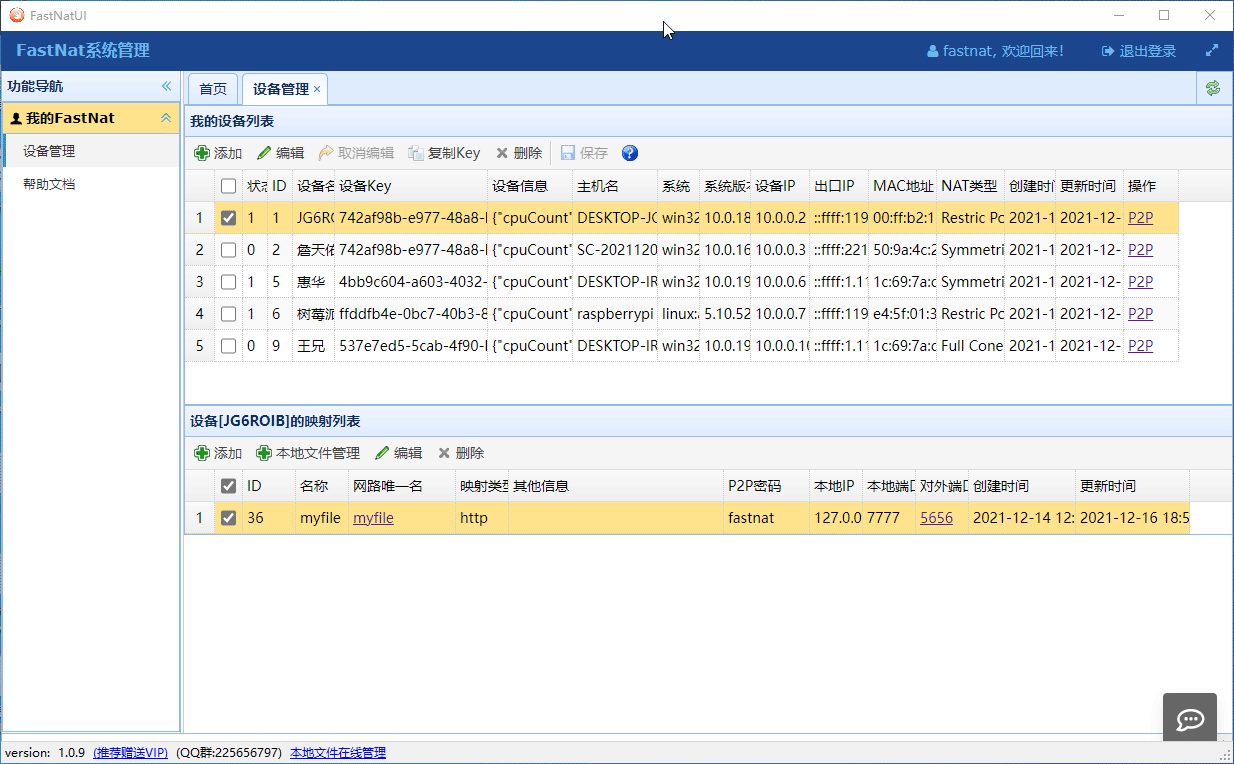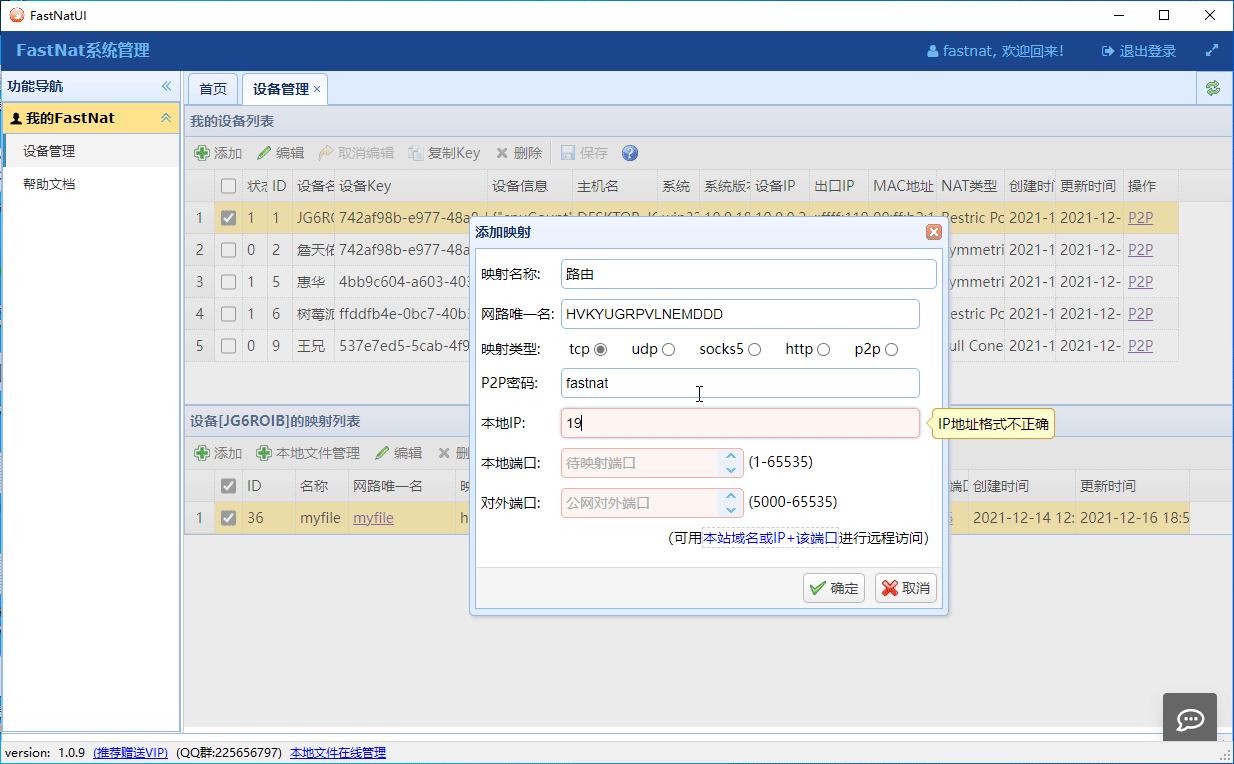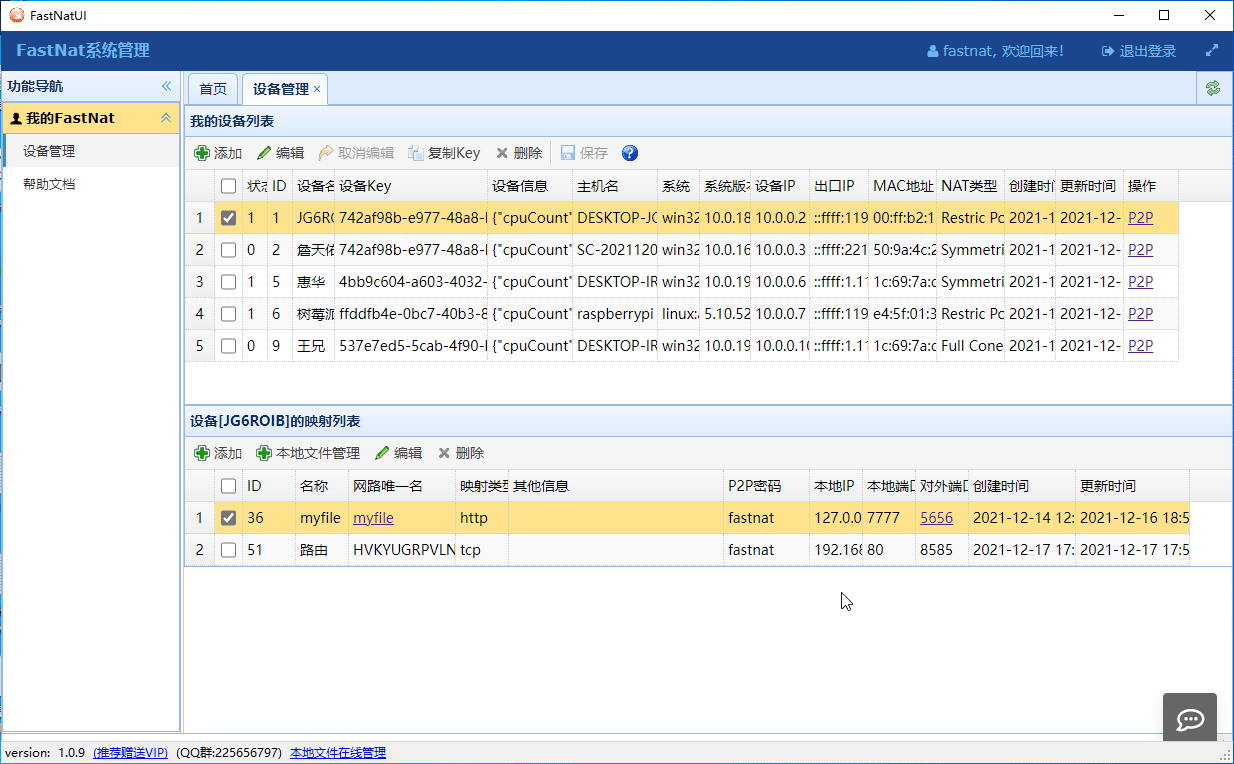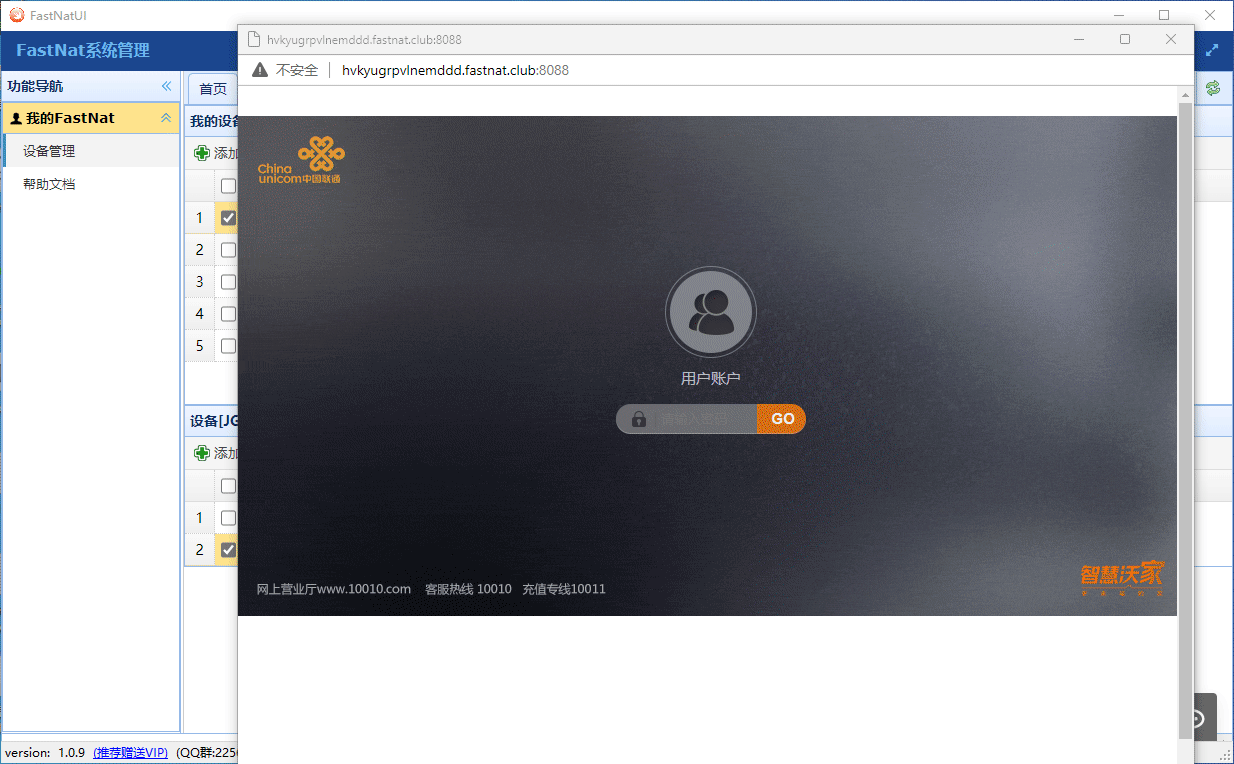
开发运维工具推荐 --- 解决远程访问局域网服务的问题。开发调试推荐
一、FastNat 可为您解决的问题1. 没公网服务器,需要发布本地的站点或网络程序到公网上,供他人访问;此项功能大大方面开发人员进行远程调试,微信小程序等开发工作进行。2. 需要远程到在其他网络中的设备,但两处的网络不…...
)
【华为OD机试 】单词倒序(C++ Java JS Python)
文章目录 题目描述输入描述输出描述备注用例题目解析C++ 解法JavaScript算法源码Java算法源码Python解法题目描述 输入单行英文句子,里面包含英文字母,空格以及,.?三种标点符号,请将句子内每个单词进行倒序,并输出倒序后的语句。 输入描述 输入字符串S,S的长度 1 ≤ N…...

PLC 诊断故障的基本原理
(1)东欢坨选煤厂机电设备故障信号主要取自开关量信号,PLC 通过开关量的通和断对设备进行故障诊断。PLC 对开关量的识别是通过输入模块来实现的。PLC 控制设备运行时,设备中的温度、压力、急停、跑偏、速度、过热以及各种按钮和行程开关的传感器与 PLC 输入模块相连接,输入模块的…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...
