机器学习复习--logistic回归简单的介绍和代码调用
最近需要复习一下机器学习相关知识,记录一下
一、简介
线性回归:h(x)=wTx+bh(x)=w^T x +bh(x)=wTx+b
logistic回归就是在线性模型的基础上加上一个sigmoid函数ggg,即h(x)=g(wTx+b)h(x)=g(w^T x+b)h(x)=g(wTx+b)。。。g(z)=1/(1+e−z)g(z)=1/(1+e^{-z})g(z)=1/(1+e−z)。
它可以将一个线性回归中的结果转化为一个概率值。此时h(x)h(x)h(x)表示的就是某件事发生的概率,我们也可以记为p(Y=1∣x)p(Y=1|x)p(Y=1∣x)
二、 逻辑回归的损失函数
逻辑回归采用的是交叉熵的损失函数。
对于一般的二分类的逻辑回归来说交叉熵函数为:J(θ)=−[yln(y′)+(1−y)ln(1−y′)]J(\theta)=-[yln(y')+(1-y)ln(1-y')]J(θ)=−[yln(y′)+(1−y)ln(1−y′)],其中y′y'y′是预测值。
实际上我们求的是训练中所有样本的损失,因此:
J(θ)=−1m∑[yiln(yi‘)+(1−yi)ln(1−yi‘)]J(\theta )=-\frac{1}{m}\sum[y_i ln(y_i`)+(1-y_i )ln(1-y_i`)] J(θ)=−m1∑[yiln(yi‘)+(1−yi)ln(1−yi‘)]
三、逻辑回归的优化方法
3.1 梯度下降
函数梯度的方向就是函数增长最快的方向,反之梯度的反方向就是函数减少最快的方向。因此我们想要计算一个函数的最小值,就朝着该函数梯度相反的方向前进。
假设我们需要优化的函数:f(X)=f(x1,...,xn)f(X)=f(x_1,...,x_n)f(X)=f(x1,...,xn)
首先我们初始化自变量,从X(0)=(x1(0),...xn(0))X^(0)=(x_1^{(0)},...x_n^{(0)})X(0)=(x1(0),...xn(0))开始。设置一个学习率η\etaη。
对于任何i>=0i>=0i>=0:
如果是最小化fff
x1i+1=x1i−η∂f∂x1(x(i))x_1^{i+1}=x_1^{i}-\eta \frac{\partial{f}}{\partial{x_1}}(x^{(i)})x1i+1=x1i−η∂x1∂f(x(i))
xni+1=xni−η∂f∂xn(x(i))x_n^{i+1}=x_n^{i}-\eta \frac{\partial{f}}{\partial{x_n}}(x^{(i)})xni+1=xni−η∂xn∂f(x(i))
反之如果求fff的最大值,则
x1i+1=x1i+η∂f∂x1(x(i))x_1^{i+1}=x_1^{i}+\eta \frac{\partial{f}}{\partial{x_1}}(x^{(i)})x1i+1=x1i+η∂x1∂f(x(i))
xni+1=xni+η∂f∂xn(x(i))x_n^{i+1}=x_n^{i}+\eta \frac{\partial{f}}{\partial{x_n}}(x^{(i)})xni+1=xni+η∂xn∂f(x(i))
3.2逻辑回归的优化
逻辑回归优化的目标函数:
J(w,b)=−1m∑[yiln(σ(wTx+b))+(1−yi)ln(1−σ(wTx+b))]J(w,b )=-\frac{1}{m}\sum[y_i ln(\sigma(w^T x +b))+(1-y_i )ln(1-\sigma(w^T x +b))]J(w,b)=−m1∑[yiln(σ(wTx+b))+(1−yi)ln(1−σ(wTx+b))]
我们需要优化参数w,bw,bw,b,从而使其在我们已知的样本X,yX,yX,y上值最小。也就是我们常说的经验风险最小。
首先我们需要对J(w,b)J(w,b)J(w,b)求导。
先令 g=σ(wTx+b)g=\sigma(w^T x +b)g=σ(wTx+b)
∂J(g)∂g=−∂∂g[yln(g)+(1−y)ln(1−g)]=−yg+1−y1−g\frac{\partial J(g)}{\partial g}=-\frac{\partial}{\partial g}[yln(g)+(1-y)ln(1-g)]=-\frac{y}{g}+\frac{1-y}{1-g} ∂g∂J(g)=−∂g∂[yln(g)+(1−y)ln(1−g)]=−gy+1−g1−y
再令:a=wTx+ba=w^T x +ba=wTx+b
∂g∂a=∂(11+e−a)∂a=−(1+e−a)−2−e−a=11+e−a1+e−a−11+e−a=σ(a)(1−σ(a))=g(1−g)\frac{\partial g}{\partial a}=\frac{\partial ({\frac{1}{1+e^{-a}}})}{\partial a}=-(1+e^{-a})^{-2}-e^{-a}=\frac{1}{1+e^{-a}}\frac{1+e^{-a}-1}{1+e^{-a}}=\sigma(a)(1-\sigma (a))=g(1-g) ∂a∂g=∂a∂(1+e−a1)=−(1+e−a)−2−e−a=1+e−a11+e−a1+e−a−1=σ(a)(1−σ(a))=g(1−g)
可以发现g=σ(a)g=\sigma(a)g=σ(a),但是ggg对aaa求导之后居然是 g(1−g)g(1-g)g(1−g),在后续的梯度下降优化中,Sigmoid函数的这个性质可以减少很多不必要的计算。
接下来求需要优化的参数w,bw,bw,b的梯度。
根据链式求导:
∂J∂w=∂J∂g∂g∂a∂a∂w=(−yg+1−y1−g)g(1−g)x=(g−y)x\frac{\partial J}{\partial w}=\frac{\partial J}{\partial g}\frac{\partial g}{\partial a}\frac{\partial a}{\partial w}=(-\frac{y}{g}+\frac{1-y}{1-g})g(1-g)x=(g-y)x ∂w∂J=∂g∂J∂a∂g∂w∂a=(−gy+1−g1−y)g(1−g)x=(g−y)x
∂J∂b=∂J∂g∂g∂a∂a∂b=(−yg+1−y1−g)g(1−g)=(g−y)\frac{\partial J}{\partial b}=\frac{\partial J}{\partial g}\frac{\partial g}{\partial a}\frac{\partial a}{\partial b}=(-\frac{y}{g}+\frac{1-y}{1-g})g(1-g)=(g-y) ∂b∂J=∂g∂J∂a∂g∂b∂a=(−gy+1−g1−y)g(1−g)=(g−y)
四、调用sklearn中的lr
import numpy as np
from sklearn import datasets
from sklearn.model_selection import train_test_split
X=datasets.load_iris()['data']
Y=datasets.load_iris()['target']
from sklearn.linear_model import LogisticRegression
X_train,X_test,y_train,y_test=train_test_split(X,Y,test_size=0.1,stratify=Y)model=LogisticRegression(penalty='l2',class_weight=None,random_state=None, max_iter=100)
model.fit(X_train,y_train)
model.predict_proba(X_test)
penalty:惩罚系数,也就是我们常说的正则化,默认为"l2",可选为l1。
class_weight:类别权重,一般我们在分类不均衡的时候使用,比如{0:0.1,1:1}代表在计算loss的时候,0类别的loss乘以0.1。这样在0类别的数据过多时候就相当于给1类别提权了。
max_iter:最大迭代次数。
五、为什么逻辑回归中经常会将特征离散化。
这个是工业界中常见的操作,一般我们不会将连续的值作为特征输入到逻辑回归的模型之中,而是将其离散成0,1变量。这样的好处有:
1:稀疏变量的内积乘法速度快,计算结果方便存储,并且容易扩展;
2:离散化后的特征对异常数据有很强的鲁棒性:比如一个特征是年龄>30是1,否则0。如果特征没有离散化,一个异常数据“年龄300岁”会给模型造成很大的干扰。
3:逻辑回归属于广义线性模型,表达能力受限;单变量离散化为N个后,每个变量有单独的权重,相当于为模型引入了非线性,能够提升模型表达能力,加大拟合;
4:离散化后可以进行特征交叉,由M+N个变量变为M*N个变量,进一步引入非线性,提升表达能力;
5:特征离散化后,模型会更稳定,比如如果对用户年龄离散化,20-30作为一个区间,不会因为一个用户年龄长了一岁就变成一个完全不同的人。当然处于区间相邻处的样本会刚好相反,所以怎么划分区间是比较重要的。
相关文章:

机器学习复习--logistic回归简单的介绍和代码调用
最近需要复习一下机器学习相关知识,记录一下 一、简介 线性回归:h(x)wTxbh(x)w^T x bh(x)wTxb logistic回归就是在线性模型的基础上加上一个sigmoid函数ggg,即h(x)g(wTxb)h(x)g(w^T xb)h(x)g(wTxb)。。。g(z)1/(1e−z)g(z)1/(1e^{-z})g(z)…...
uniapp小程序接入腾讯地图sdk
新建一个项目。配置uniapp配置文件设置小程序的appid注意:匿名用户可能存在地理定位失效。查uniapp官网官网->apiuni.getLocation(OBJECT) 获取当前的地理位置、速度。属性:success匿名函数返回值:uni.getLocation({type: gcj02,success: …...

总结JavaScript中的条件判断与比较运算
一、条件判断 JavaScript 中有三种方法可以用来进行条件判断: 1、使用 if-else 语句。这种方法用于在特定条件为 true 时执行一段代码,否则执行另一段代码。例如: let a 5; if (a > 10) {console.log("a is greater than 10"…...

算法练习-排序(一)
算法练习-排序(一) 文章目录算法练习-排序(一)1 排序算法1.1 冒泡排序1.1.1代码1.2插入排序1.2.1代码1.3 选择排序1.3.1代码1.4归并排序1.4.1代码1.5 快速排序1.5.1 思路1.5.2 代码2 题目2.1 特殊排序2.1.1 题目2.1.2 题解2.2 数组中的第k个最大元素2.2.1 题目2.2.2 题解2.3 对…...

CentOS7.6快速安装Docker
快速安装 官网安装参考手册:https://docs.docker.com/install/linux/docker-ce/centos/ 确定你是CentOS7及以上版本,yum是在线安装! [rootVM-4-5-centos ~]# cat /etc/redhat-releaseCentOS Linux release 7.6.1810 (Core)接下来您只管自上向下执行命令即可&#x…...
CentOS 7安装N卡驱动和CUDA和cuDNN
前言系统一开始是CentOS 7.6,安装依赖时yum给的内核文件的版本号和uname -r的结果不一样,这时不能直接装依赖,装上后后面装驱动时会报错找不到内核头文件(最开始我直接装依赖了,以为高版本兼容低版本,然后装驱动时报错…...

Java开发 - 分页查询初体验
前言在上一篇,我们对es进行了深入讲解,相信看过的小伙伴已经能基本掌握es的使用方法,我们知道,es主要针对的是搜索条件,在这方面es具有无可比拟的优势,但我们也会注意到,有时候搜索条件过于宽泛…...
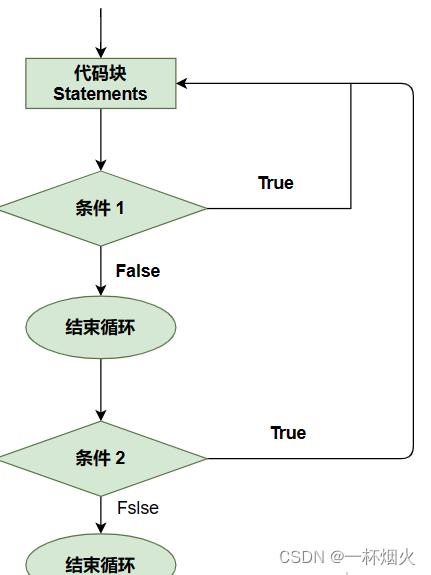
C语言循环语句do while和嵌套循环语句讲解
C do…while 循环 不像 for 和 while 循环,它们是在循环头部测试循环条件。在 C 语言中,do…while 循环是在循环的尾部检查它的条件。 do…while 循环与 while 循环类似,但是 do…while 循环会确保至少执行一次循环。 语法 C 语言中 do…w…...
【7】:拼接图像)
【计算机视觉】OpenCV 4高级编程与项目实战(Python版)【7】:拼接图像
我们已经知道,图像是通过数组描述的,那么拼接图像其实就是拼接数组。NumPy提供了2个拼接数组的函数,分别是hstack函数和vstack函数,这两个拼接函数可以将两个数组水平和垂直拼接在一起,也就相当于将两幅图像水平和垂直拼接在一起,本节将详细讲解如何使用这两个函数水平拼…...
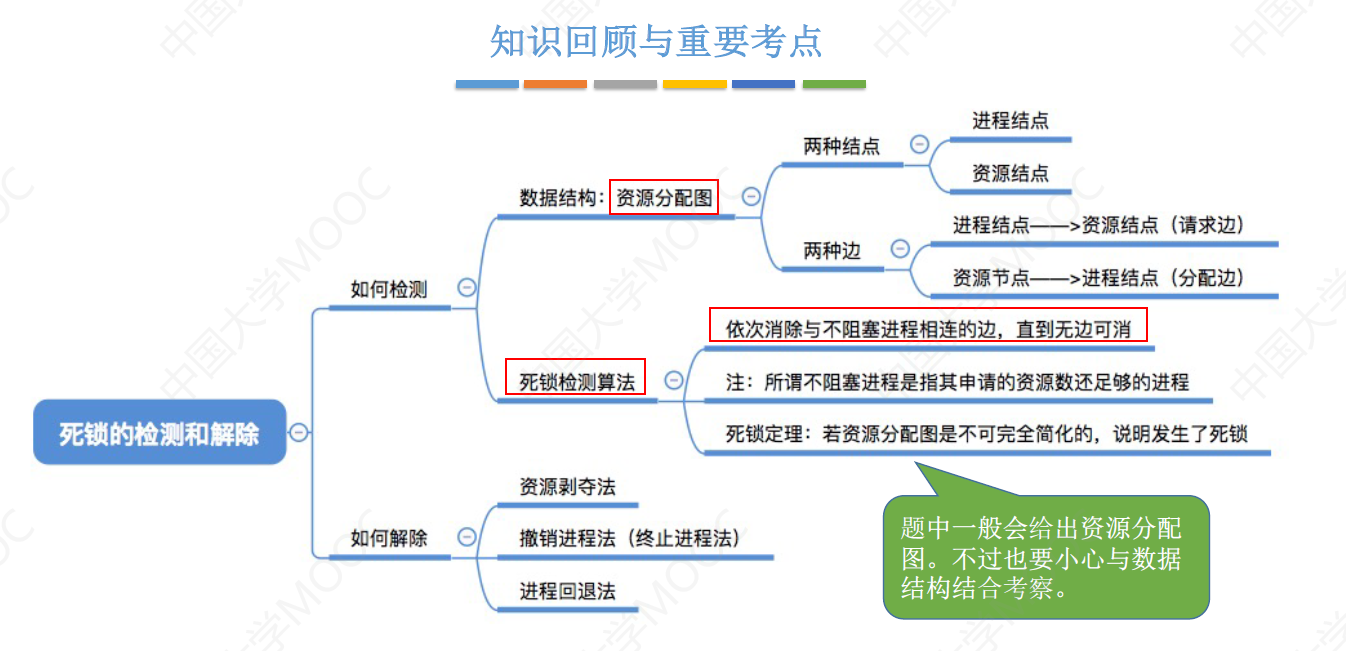
王道操作系统课代表 - 考研计算机 第二章 进程与线程 究极精华总结笔记
本篇博客是考研期间学习王道课程 传送门 的笔记,以及一整年里对 操作系统 知识点的理解的总结。希望对新一届的计算机考研人提供帮助!!! 关于对 “进程与线程” 章节知识点总结的十分全面,涵括了《操作系统》课程里的全…...

C++修炼之练气期三层——函数重载
目录 1.引例 2.函数重载的概念 3.C支持函数重载的原理 1.引例 倘若现在要实现一个加法计算器,用C语言实现的话我们会选择这样的方式: int Add_int(int a, int b) {return a b; }double Add_double(double a, double b) {return a b; } 在使用加…...

在linux上运行jar程序操作记录
1.文件传送 使用ftp把打包后的项目jar包上传到linux服务器的目录上(这里有两个文件,一个pengning.jar,一个配置文件application.yml) 2.进入目录并运行程序 打开终端,进入pengning.jar所在的目录 [rootcampus /]# [rootcampu…...
:实时操作系统RTOS和通用操作系统GPOS的区别)
【STM32】入门(十二):实时操作系统RTOS和通用操作系统GPOS的区别
1、简述 实时操作系统(RTOS,Real Time Operating System) 通用操作系统(GPOS,General Purpose Operating System) 2、区别 1)任务 实时操作系统:使用分时设计,其中每个任务被分配一小段时间,在切换到另一…...

2023-3-1刷题情况
在网格图中访问一个格子的最少时间 题目描述 给你一个 m x n 的矩阵 grid ,每个元素都为 非负 整数,其中 grid[row][col] 表示可以访问格子 (row, col) 的 最早 时间。也就是说当你访问格子 (row, col) 时,最少已经经过的时间为 grid[row][…...

Web前端学习:五 - 练习
四二-四八:baidu糯米 44-48 1、写法1 (1)a.movie1 .Navigation .recommend .listbanner a.movie1{background: url(img/h_1.jpg) no-repeat 63px 9px;}表示a标签且class为movie1的元素 如: <a href"#" class&quo…...

软件测试之测试用例设计方法—等价类划分法
测试用例设计方法—等价类划分法 掌握常用测试用例设计方法,再结合测试用例的要素能给快速的实现测试用例的设计和编写.但是由于软件系统大小的不同我们不可能把所有的单个或组合的情况都进行测试,所以我们测试时应该根据不同的场景设计不同的测试用例,尽可能的覆盖到全部需要…...
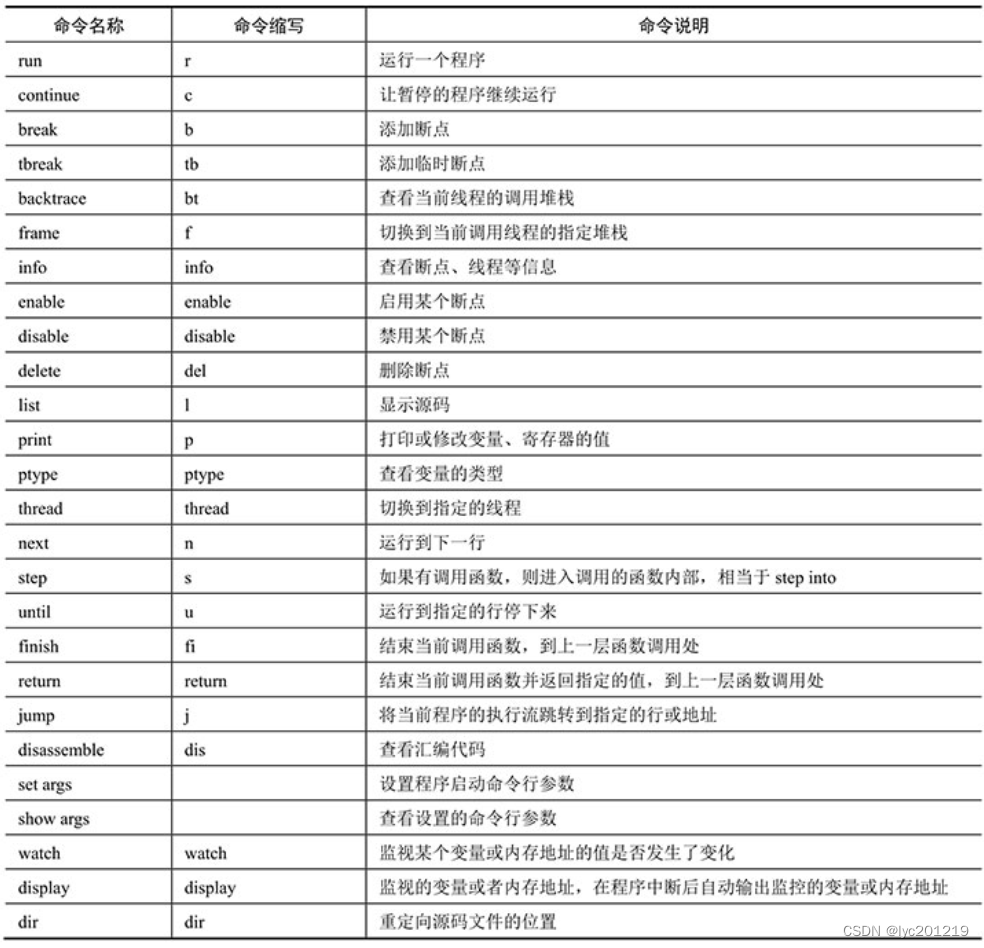
gdb常用命令详解
gdb常用调试命令概览和说明 run命令 在默认情况下,gdbfilename只是attach到一个调试文件,并没有启动这个程序,我们需要输入run命令启动这个程序(run命令被简写成r)。如果程序已经启动,则再次输入 run 命令…...
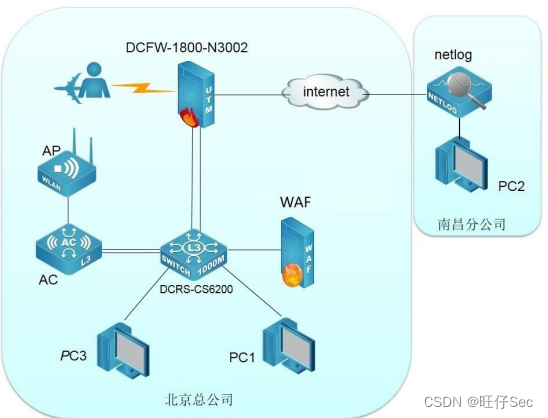
2022 年江西省职业院校技能大赛高职组“信息安全管理与评估”赛项样题
2022 年江西省职业院校技能大赛高职组 “信息安全管理与评估”赛项样题 一、 赛项信息 第一场比赛: 竞赛阶段 任务阶 段 竞赛任务 竞赛时 间 分值 第一阶段 任务 1 网络平台搭建 90 平台搭建与安全 任务 2 网络安全设备配置与防护 210 设备配置防护…...
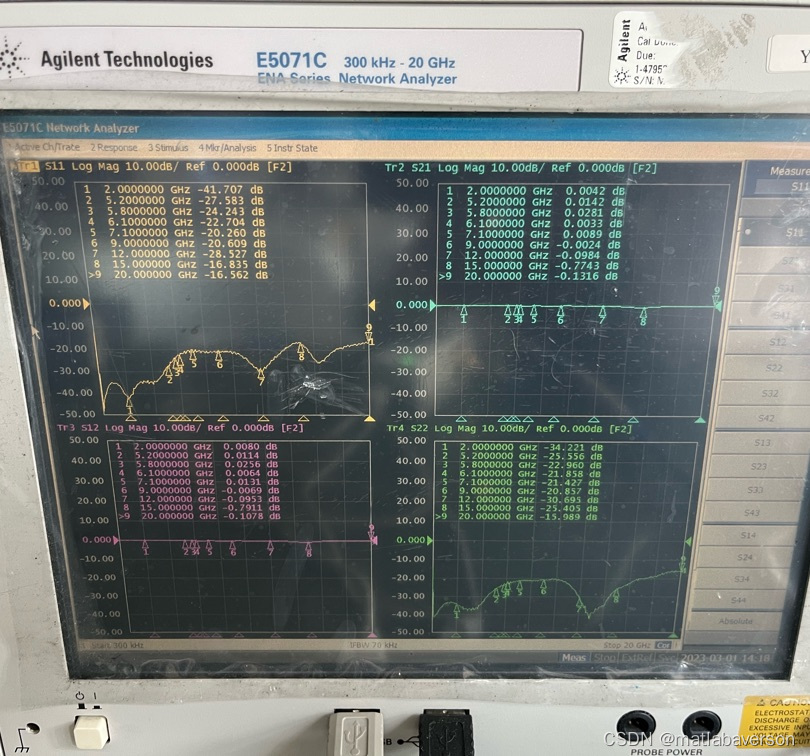
射频调试的习惯
三月开工了,一个月的调试即将开始。其实调试的重心是测试,核心的推动力是做事的习惯和思维。测试很重要,数据不对,能力和时间都浪费了上面了。测试的问题初步解完了,今天吃饭的时候碰到大领导。领导好忙,我…...
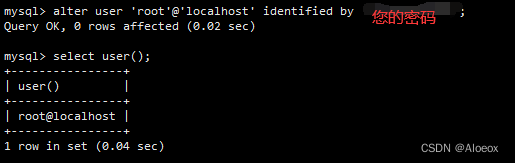
centos7上安装mysql8.0
1、检查一下自己电脑上安装了哪些mysql [rootlocalhost ~]# find / -name mysql 2、把安装的mysql全部删掉 [rootlocalhost ~]# rm -rf /usr/lib64/mysql/ [rootlocalhost ~]# rm -rf /usr/local/mysql/ [rootlocalhost ~]# rm -rf /etc/selinux/targeted/active/modules/100…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...

Python实现简单音频数据压缩与解压算法
Python实现简单音频数据压缩与解压算法 引言 在音频数据处理中,压缩算法是降低存储成本和传输效率的关键技术。Python作为一门灵活且功能强大的编程语言,提供了丰富的库和工具来实现音频数据的压缩与解压。本文将通过一个简单的音频数据压缩与解压算法…...
