使用正则表达式时-可能会导致性能下降的情况
目录
前言
正则表达式引擎
NFA自动机的回溯
解决方案
-
前言
- 正则表达式是一个用正则符号写出的公式,程序对这个公式进行语法分析,建立一个语法分析树,再根据这个分析树结合正则表达式的引擎生成执行程序(这个执行程序我们把它称作状态机,也叫状态自动机),用于字符匹配
- 使用不恰当的正则表达式可能会导致很严重的性能问题
- 比如:
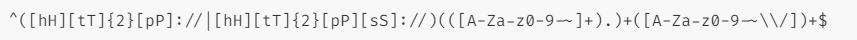
- 这个正则表达式看起来没什么问题,它可以分为三个部分:
- 第一部分匹配 http 和 https 协议,第二部分匹配 www. 字符,第三部分匹配许多字符
- 其实这里会导致 CPU 使用率高的关键原因就是:Java 正则表达式使用的引擎实现是 NFA 自动机,这种正则表达式引擎在进行字符匹配时会发生回溯backtracking
- 而一旦发生回溯,那其消耗的时间就会变得很长,有可能是几分钟,也有可能是几个小时,时间长短取决于回溯的次数和复杂度
-
正则表达式引擎
- 正则表达式引擎就是一套核心算法,用于建立状态机
- 简单地说,实现正则表达式引擎的有两种方式:DFA 自动机(Deterministic Final Automata 确定型有穷自动机)和 NFA 自动机(Non deterministic Finite Automaton 不确定型有穷自动机)
- 简单来讲,NFA 对应的是正则表达式主导的匹配,而 DFA 对应的是文本主导的匹配
- 简单来讲,DFA 自动机的时间复杂度是线性的,更加稳定,但是功能有限;而 NFA 的时间复杂度比较不稳定,有时候很好,有时候不怎么好,好不好取决于你写的正则表达式;但是胜在 NFA 的功能更加强大,所以包括 Java、.NET、Perl、Python、Ruby、PHP 等语言都使用了 NFA 去实现其正则表达式
- 那 NFA 自动机到底是怎么进行匹配的呢?我们以下面的字符和表达式来举例说明:

- 要记住一个很重要的点,即:NFA 是以正则表达式为基准去匹配的
- 也就是说,NFA 自动机会读取正则表达式的一个一个字符,然后拿去和目标字符串匹配,匹配成功就换正则表达式的下一个字符,否则继续和目标字符串的下一个字符比较
- 首先,拿到正则表达式的第一个匹配符:d
- 于是拿去和字符串的字符进行比较,字符串的第一个字符是T,不匹配,换下一个
- 第二个是o,也不匹配,再换下一个
- 第三个是d,匹配了,那么就读取正则表达式的第二个字符:a
- 读取到正则表达式的第二个匹配符:a
- 拿着继续和字符串的第四个字符 a 比较,又匹配了
- 那么接着读取正则表达式的第三个字符:y
- 读取到正则表达式的第三个匹配符:y
- 拿着继续和字符串的第五个字符 y 比较,又匹配了
- 尝试读取正则表达式的下一个字符,发现没有了,那么匹配结束
- 上面这个匹配过程就是 NFA 自动机的匹配过程,但实际上的匹配过程会比这个复杂非常多,但其原理是不变的
-
NFA自动机的回溯
- 了解了 NFA 是如何进行字符串匹配的,接下来我们就可以讲讲这篇文章的重点了:回溯
- 为了更好地解释回溯,我们同样以下面的例子来讲解:

- 上面的这个例子的目的比较简单,匹配以 a 开头,以 c 结尾,中间有 1-3 个 b 字符的字符串
- NFA 对其解析的过程是这样子的:
- 首先,读取正则表达式第一个匹配符 a 和 字符串第一个字符 a 比较,匹配了
- 于是读取正则表达式第二个字符
- 读取正则表达式第二个匹配符 b{1,3} 和字符串的第二个字符 b 比较,匹配了
- 但因为 b{1,3} 表示 1-3 个 b 字符串,以及 NFA 自动机的贪婪特性(也就是说要尽可能多地匹配),所以此时并不会再去读取下一个正则表达式的匹配符,而是依旧使用 b{1,3} 和字符串的第三个字符 b 比较,发现还是匹配
- 于是继续使用 b{1,3} 和字符串的第四个字符 c 比较,发现不匹配了
- 此时就会发生回溯
- 发生回溯是怎么操作呢?
- 发生回溯后,我们已经读取的字符串第四个字符 c 将被吐出去,指针回到第三个字符串的位置
- 之后,程序读取正则表达式的下一个操作符 c,读取当前指针的下一个字符 c 进行对比,发现匹配
- 于是读取下一个操作符,但这里已经结束了
- 下面我们回过头来看看前面的那个校验 URL 的正则表达式:

- 出现问题的 URL 是:

- 我们把这个正则表达式分为三个部分:
- 第一部分:校验协议;^([hH][tT]{2}[pP]://|[hH][tT]{2}[pP][sS]://)
- 第二部分:校验域名;(([A-Za-z0-9-~]+).)+
- 第三部分:校验参数;([A-Za-z0-9-~\\/])+$
- 我们可以发现正则表达式校验协议 http:// 这部分是没有问题的,但是在校验 www.fapiao.com 的时候,其使用了 xxxx. 这种方式去校验
- 那么匹配过程是这样的:
- 匹配到 www.
- 匹配到 fapiao.
- 匹配到 com/dzfp-web/pdf/download?request=6e7JGm38jf.....,你会发现因为贪婪匹配的原因,所以程序会一直读后面的字符串进行匹配,最后发现没有点号,于是就一个个字符回溯回去了
- 这是这个正则表达式存在的第一个问题
- 另外一个问题是在正则表达式的第三部分,我们发现出现问题的 URL 是有下划线(_)和百分号(%)的,但是对应第三部分的正则表达式里面却没有
- 这样就会导致前面匹配了一长串的字符之后,发现不匹配,最后回溯回去
- 这是这个正则表达式存在的第二个问题
-
解决方案
- 明白了回溯是导致问题的原因之后,其实就是减少这种回溯,你会发现如果我在第三部分加上下划线和百分号之后,程序就正常了

- 运行上面的程序,立刻就会打印出match!!
- 但这是不够的,如果以后还有其他 URL 包含了乱七八糟的字符呢,我们难不成还再修改一遍
- 肯定不现实
- 其实在正则表达式中有这么三种模式:贪婪模式、懒惰模式、独占模式
- 在关于数量的匹配中,有 + ? * {min,max} 四种两次,如果只是单独使用,那么它们就是贪婪模式
- 如果在他们之后多加一个 ? 符号,那么原先的贪婪模式就会变成懒惰模式,即尽可能少地匹配
- 但是懒惰模式还是会发生回溯现象
- 例如下面这个例子:

- 正则表达式的第一个操作符 a 与 字符串第一个字符 a 匹配,匹配成功
- 于是正则表达式的第二个操作符 b{1,3}? 和 字符串第二个字符 b 匹配,匹配成功
- 因为最小匹配原则,所以拿正则表达式第三个操作符 c 与字符串第三个字符 b 匹配,发现不匹配
- 于是回溯回去,拿正则表达式第二个操作符 b{1,3}? 和字符串第三个字符 b 匹配,匹配成功
- 于是再拿正则表达式第三个操作符 c 与字符串第四个字符 c 匹配,匹配成功;于是结束
- 如果在他们之后多加一个 + 符号,那么原先的贪婪模式就会变成独占模式,即尽可能多地匹配,但是不回溯
- 于是乎,如果要彻底解决问题,就要在保证功能的同时确保不发生回溯
- 将上面校验 URL 的正则表达式的第二部分后面加多了个 + 号,即变成这样:

- 这样之后,运行原有的程序就没有问题了
相关文章:

使用正则表达式时-可能会导致性能下降的情况
目录 前言 正则表达式引擎 NFA自动机的回溯 解决方案 前言 正则表达式是一个用正则符号写出的公式,程序对这个公式进行语法分析,建立一个语法分析树,再根据这个分析树结合正则表达式的引擎生成执行程序(这个执行程序我们把它称作状态机&a…...
Maven生命周期
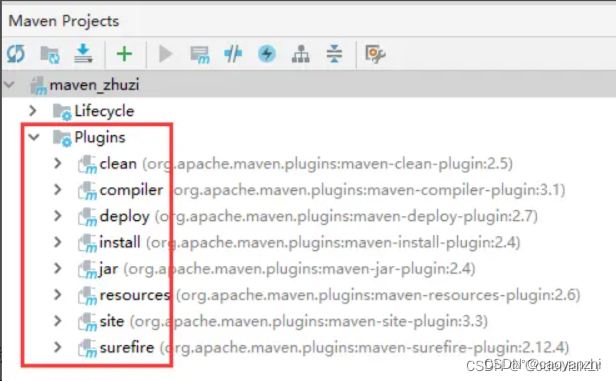
Maven生命周期 通过IDEA工具的辅助,能很轻易看见Maven的九种生命周期命令,如下: 双击其中任何一个,都会执行相应的Maven构建动作,为啥IDEA能实现这个功能呢?道理很简单,因为IDEA封装了Maven提供…...

深度学习(五):pytorch迁移学习之resnet50
1.迁移学习 迁移学习是一种机器学习方法,它通过将已经在一个任务上学习到的知识应用到另一个相关任务上,来改善模型的性能。迁移学习可以解决数据不足或标注困难的问题,同时可以加快模型的训练速度。 迁移学习的核心思想是将源领域的知识迁…...

面试官:说说synchronized与ReentrantLock的区别
程序员的公众号:源1024,获取更多资料,无加密无套路! 最近整理了一波电子书籍资料,包含《Effective Java中文版 第2版》《深入JAVA虚拟机》,《重构改善既有代码设计》,《MySQL高性能-第3版》&…...
数据结构学习笔记——广义表
目录 一、广义表的定义二、广义表的表头和表尾三、广义表的深度和长度四、广义表与二叉树(一)广义表表示二叉树(二)广义表表示二叉树的代码实现 一、广义表的定义 广义表是线性表的进一步推广,是由n(n≥0&…...
)
为什么每次optimizer.zero_grad()
当你训练一个神经网络时,每一次的传播和参数更新过程可以被分解为以下步骤: 1前向传播:网络对输入数据进行操作,最终生成输出。这个过程会基于当前的参数(权重和偏差)计算出一个或多个损失函数的值。 2计…...

一个页面从输入 URL 到页面加载显示完成,这个过程中都发生了什么
一个页面从输入URL到加载显示完成经历了以下过程: DNS解析:浏览器会解析URL中的域名,将其转换为对应的IP地址。如果浏览器缓存中存在该域名的IP地址,则跳过DNS解析步骤。 建立TCP连接:通过解析得到的IP地址࿰…...

iOS ------ UICollectionView
一,UICollectionView的简介 UICollectionView是iOS6之后引入的一个新的UI控件,它和UITableView有着诸多的相似之处,其中许多代理方法都十分类似。简单来说,UICollectionView是比UITbleView更加强大的一个UI控件,有如下…...
ElasticSearch知识体系详解
1.介绍 ElasticSearch是基于Lucene的开源搜索及分析引擎,使用Java语言开发的搜索引擎库类,并作为Apache许可条款下的开放源码发布,是当前流行的企业级搜索引擎。 它可以被下面这样准确的形容: 一个分布式的实时文档存储…...

Linux自启服务提示:systemd[1]: *.service: main process exited, code=exited, status=1问题
这两天一直在沉迷于配脚本,由于服务器很多,所以我都是从一台服务器上配置好的脚本直接copy到另一台服务器,按说完全一样的脚本一样的操作,那么应该是一样的执行结果 but, Gul’dan,代…我重启服务器后服务并没有正常启…...
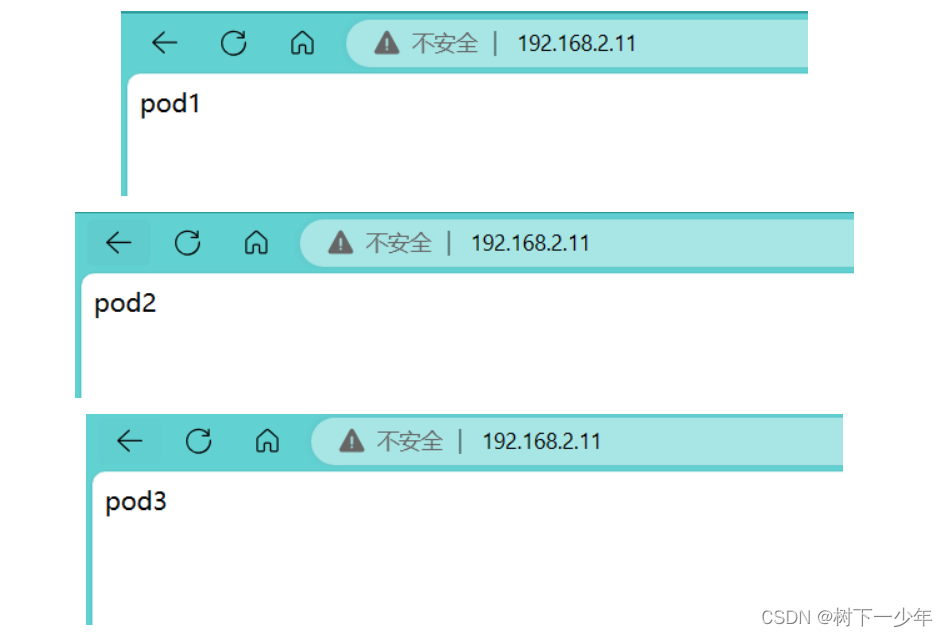
LoadBalancer将服务暴露到外部实现负载均衡purelb-layer2模式配置介绍
目录 一.purelb简介 1.简介 2.purelb的layer2工作模式特点 二.layer2的配置演示 1.首先准备ipvs和arp配置环境 2.purelb部署开始 (1)下载purelb-complete.yaml文件并应用 (2)查看该有的资源是否创建完成并运行 ÿ…...
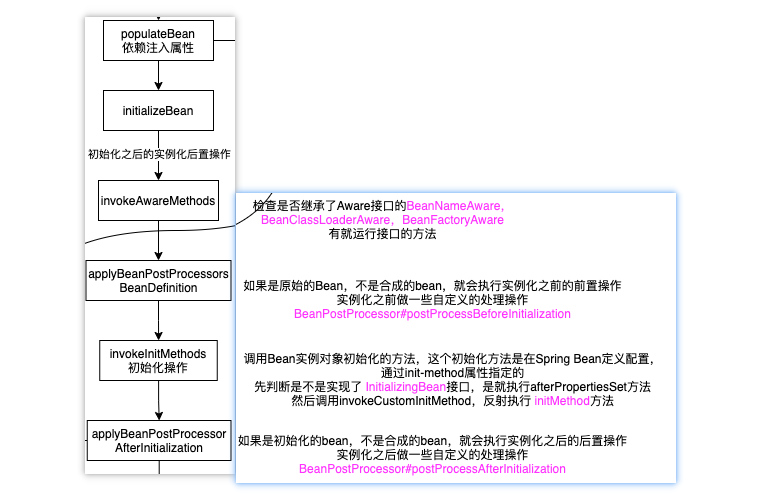
Spring Bean的生命周期各阶段详解附源码
目录 Bean的生命周期Bean定义阶段Bean实例化阶段Bean属性注入阶段Bean初始化阶段Bean销毁阶段 Bean的生命周期 bean的生命周期,我们都知道大致是分为:bean定义,bean的实例化,bean的属性注入,bean的初始化以及bean的销毁…...
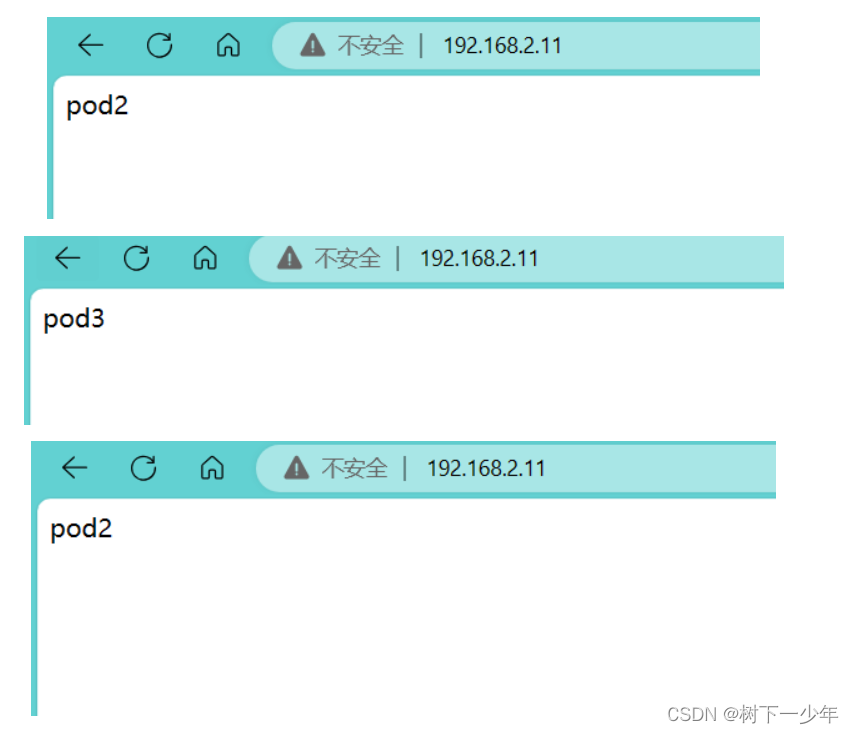
LoadBalancer将服务暴露到外部实现负载均衡Openelb-layer2模式配置介绍
目录 一.openelb简介 二.主要介绍layer2模式 1.简介 2.原理 3.部署 (1)先在集群master上开启kube-proxy的strictARP (2)应用下载openelb.yaml(需要修改镜像地址) (3)编写yam…...

Android异步之旅:探索IntentService
1.介绍IntentService IntentService是Android中的一个Service类,用于在后台执行耗时操作,而不会阻塞UI线程。它封装了HandlerThread和Handler,使得我们可以方便地在后台执行任务,而不需要自己管理线程和消息处理。 以下是 Intent…...
)
131.类型题-计算数学序列的和,请编写函数fun,其功能是S=……【满分解题代码+详细分析】(数学序列的和类型题-C/C++JavaPython实现)
文章目录 131.类型题-计算数学序列的和:计算并输出一.题目1.1 解题思路二.解题代码2.1 C/C++解题代码2.2 python解题代码2.3 Java解题代码三.解题代码仔细分析3.1 C/C++解题代码仔细分析3.2 Java解题代码仔细分析3.3 Python解题代码仔细分析四.本类型题解题诀窍五.寄语131.类型…...
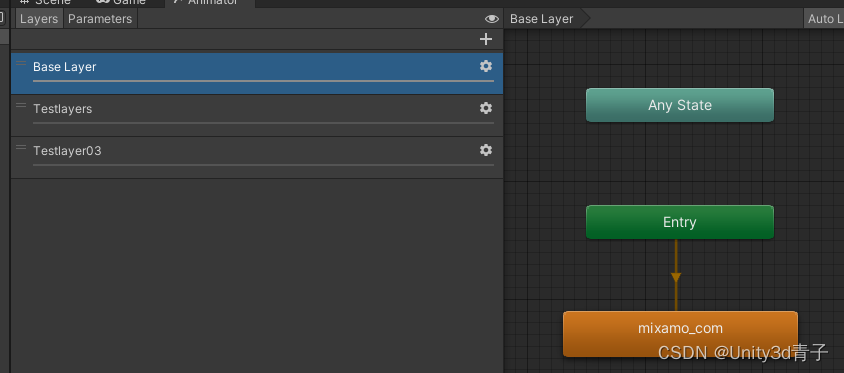
【Unity动画】状态机中层的融合原理与用法详解
1. 状态机概念介绍 在Unity中,动画状态机(Animator State Machine)是一种强大的工具,用于控制游戏对象的动画行为。动画状态机由多个动画状态Animation和过渡条件Transition、层组成!而层(Layersÿ…...

等保之道:从基础出发,解密网站防护的重要性
随着数字化时代的推进,网站安全问题日益凸显。网站被攻击不仅会导致信息泄漏、服务中断,还可能损害用户信任和企业声誉。为了更好地解决这一问题,我们需从等保的角度审视网站防护,全面提升网络安全水平。 等保背景 等保࿰…...

7. 系统信息与系统资源
7. 系统信息与系统资源 1. 系统信息1.1 系统标识 uname()1.2 sysinfo()1.3 gethostname()1.4 sysconf() 2. 时间、日期2.1 Linux 系统中的时间2.1.1 Linux 怎么记录时间2.1.2 jiffies 的引入 2.2 获取时间 time/gettimeofday2.2.1 time()2.2.2 gettimeofday() 2.3 时间转换函数…...

【重点】【滑动窗口】239. 滑动窗口最大值
题目 也可参考:剑指offer——面试题65:滑动窗口的最大值 class Solution {public int[] maxSlidingWindow(int[] nums, int k) {int[] res new int[nums.length - k 1];Deque<Integer> q new LinkedList<>();int inx 0;while (inx <…...

d3dx9_43.dll丢失原因以及5个解决方法详解
在电脑使用过程中,我们可能会遇到一些错误提示,其中之一就是“d3dx9_43.dll缺失”。这个错误提示通常表示我们的电脑上缺少了DirectX的一个组件,而DirectX是游戏和多媒体应用所必需的软件。本文将介绍d3dx9_43.dll缺失对电脑的影响以及其原因…...

celldex包深度解析:如何选择最适合你研究的参考数据集?
celldex包深度解析:如何选择最适合你研究的参考数据集? 如果你正在单细胞转录组数据分析的海洋里航行,那么“细胞类型注释”这个任务,大概率是你绕不开的挑战。面对成千上万个细胞,每个都表达着数万个基因,…...

LKT4304加密芯片在工业PLC控制器中的安全应用案例
在工业自动化领域,可编程逻辑控制器(PLC)作为产线核心控制单元,其运行的控制程序直接决定设备动作逻辑与生产安全。然而,PLC固件常面临被逆向破解、非法复制或恶意篡改的风险——攻击者可能植入后门指令导致设备异常停…...

C4D接入腾讯混元AI:3D建模进入Text-to-3D时代
2026年3月,在巴塞罗那举行的世界移动通信大会(MWC 2026)上,Maxon正式宣布了一项足以改写3D创作流向的决定:与腾讯云达成战略合作,将腾讯混元(HY)3D全局AI引擎深度集成至Cinema 4D&am…...

MongoDB分片集群实战:从零搭建高可用分布式数据库
1. 为什么你需要一个MongoDB分片集群? 如果你正在读这篇文章,我猜你大概率已经遇到了单台MongoDB服务器的瓶颈。可能是磁盘空间快满了,加硬盘也解决不了根本问题;也可能是查询速度越来越慢,即使加了索引,面…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...
