数据结构学习笔记——广义表
目录
- 一、广义表的定义
- 二、广义表的表头和表尾
- 三、广义表的深度和长度
- 四、广义表与二叉树
- (一)广义表表示二叉树
- (二)广义表表示二叉树的代码实现
一、广义表的定义
广义表是线性表的进一步推广,是由n(n≥0)个数据元素组成的有限序列。线性表中的数据元素只能是单个元素(原子),它是不可分割的,而广义表中的数据元素既可以是原子,也可以是一个广义表(包括空表和非空表),广义表通过圆括号“()”括起来,通过逗号“,”隔开表中的各个数据元素。

一个n维数组可以看成元素是n-1维数组的广义表,广义表的元素都是n-1维数组。广义表满足线性表的特征,只是其中的元素是原子或广义表(子表),分别只有一个表头元素和表尾元素,表头元素有后继但是没有前驱,表尾元素有前驱但是没有后继,剩下每个元素都有唯一的前驱和后继。
二、广义表的表头和表尾
广义表是可以递归的,一个广义表也可以是其自身的子表,广义表中的第一个元素称为广义表的表头,而剩余数据元素组成的表称为广义表的表尾,广义表的表头和表尾可以看作通过函数head()和tail()对广义表操作。例如,已知广义表S=(((a)),(b),c,(a),(((d,e)))),通过head()和tail()取出元素e的操作如下:
head(tail(head(head(head(tail(tail(tail(tail(A)))))))))
任何一个非空广义表,表头可能是单个元素(原子)或广义表,但表尾只可能是广义表,其原因是广义表的取表尾tail()是非空广义表除去表头元素后,剩余元素组成的表,所以不可能是原子。
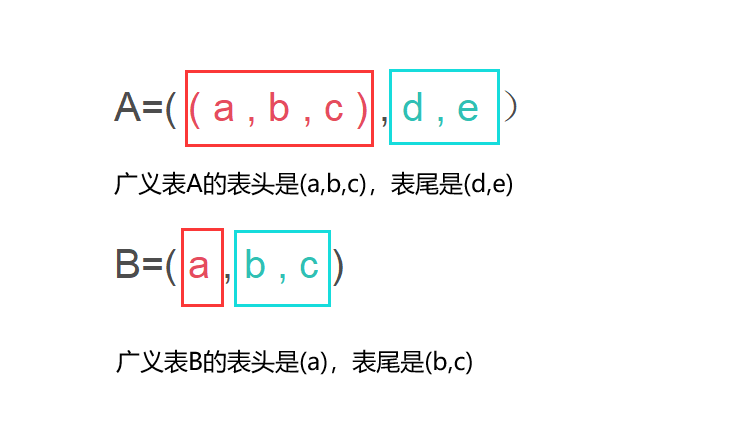
例如,C=(a,b,c,d,e,f,g),该广义表的表头是(a),表尾是(b,c,d,e,f,g);
例如,D=((a,b),((c,d,e),(f,g,h))),该广义表的表头是(a,b),表尾是((c,d,e),(f,g,h))。
另外,若一个广义表为空,则为一个空表。例如,E=( ),F=(( )),广义表E是一个空表,只有非空广义表才能取表头,广义表F的表头和表尾都是()。
三、广义表的深度和长度
- 广义表的深度通过
括号的层数求得,而长度是广义表中所含元素的个数。【深度层数,长度个数】
例如,一个空广义表G=(),括号层数为1,所以广义表的深度为1,而由于是空表,所以广义表的长度为0;
例如,一个广义表H=((a,b),(c,(d,e))),括号层数为3,所以广义表的深度为3,最高层为(c,(d,e)),逗号隔开了原子( c )和广义表( d,e ),元素个数为2,所以广义表的长度为2。
例如,一个广义表I=((),(a),(b,c,(d),((d,f)))),由于括号的最大层数为4,所以广义表的深度为4,可知广义表有三个元素,分别是()、(a)、(b,c,(d),((d,f))),元素个数为3,所以广义表的长度为3。
例如,设广义表J=(( ),( )),对广义表J,head(J)=( ),tail(J)=(( )),括号的最大层数为2,所以广义表的深度为2,广义表有两个元素,分别是()、(),元素个数为2,所以广义表长度为2。
注:这里的Tail(J)=(( )),而不是( )。
四、广义表与二叉树
(一)广义表表示二叉树
根据广义表中“ 数据元素既可以是原子,也可以是一个广义表(包括空表和非空表) ”这一点可以来表示二叉树,即通过(根结点,根结点的广义表)的形式来表示,其中可以嵌套。
例如,下面是一个满二叉树:
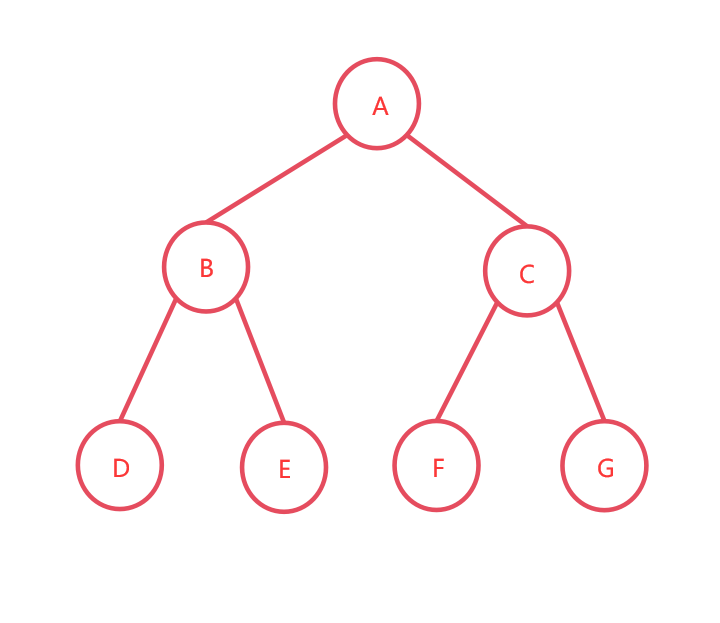
通过广义表表示该二叉树:
(A , ( B , ( D , E ) ) , ( C , ( F , G ) ) ) )
这个二叉树的解释如下:
根结点是A,它的左孩子是B,B的左孩子是D,B的右孩子是E。
根结点A的右孩子是C,C的左孩子是F,C的右孩子是G。
(二)广义表表示二叉树的代码实现
通过广义表来显示建立的二叉树,一个非空的二叉树T,当对于左孩子结点或右孩子结点时,此时输出一个左括号“(”,递归处理左子树,输出一个“,”用于隔开结点,然后递归处理右子树,输出一个右括号“)”,从而完成一个根结点以下的两个左/右结点处理,代码如下:
/*广义表输出二叉树*/
void ShowTree(BTree T) {if(T!=NULL) {//当二叉树不为空时printf("%c",T->data); //输入出该结点的数据域if(T->lchild!=NULL) { //若该结点的左子树不为空printf("("); //输出一个左括号ShowTree(T->lchild); //通过递归继续输出结点的左子树结点下的各结点if(T->rchild!=NULL) { //若该结点右子树不为空printf(","); //输出一个逗号ShowTree(T->rchild); //通过递归继续输出结点的右子树结点下的各结点}printf(")"); //输出一个右括号} else { //若左子树为空,右子树不为空if(T->rchild!=NULL) {printf("("); //输出一个左括号ShowTree(T->lchild); //通过递归继续输出结点的左子树结点下的各结点if(T->rchild!=NULL) { //若该结点的右子树不为空 printf(","); //输出一个逗号ShowTree(T->rchild); //通过递归继续输出结点的右子树结点下的各结点}printf(")"); //输出一个右括号}}}
}
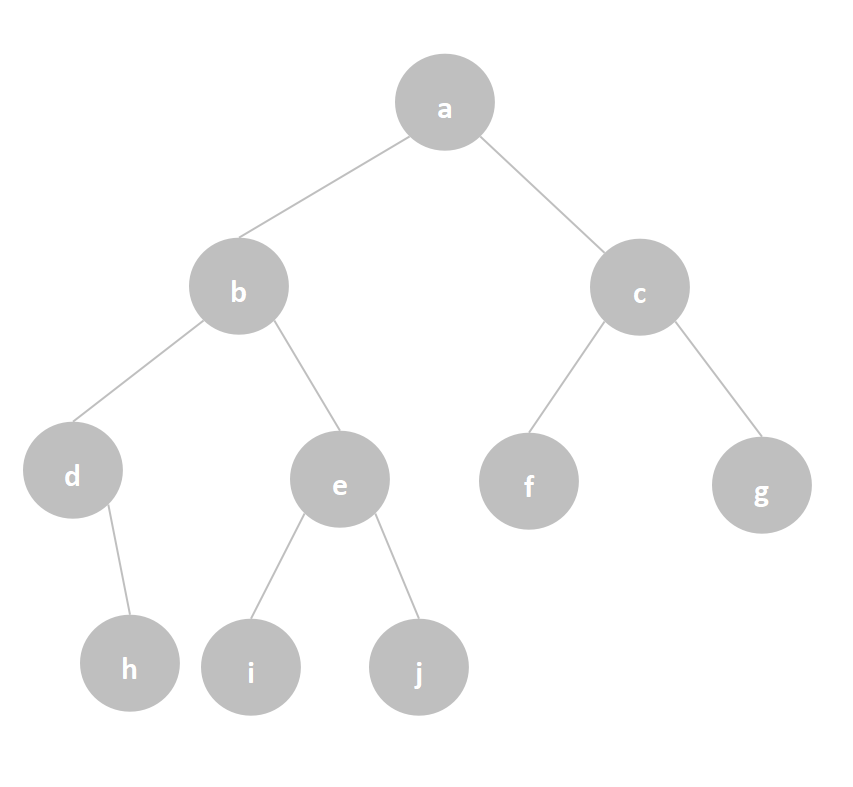
例如,一个二叉树如下图,通过链式存储结构实现建立二叉树并输出。
代码如下:
#include <stdio.h>
#include <malloc.h>
/*1、二叉树的定义*/
typedef struct BNode {int data; //数据域struct BNode *lchild,*rchild; //左孩子、右孩子指针
} *BTree;/*2、二叉树的建立*/
BTree CreateTree() {BTree T;char ch;scanf("%c",&ch);getchar(); //getchar()用于接收每次输入字符结点后的回车符,从而以便输入下一个字符结点if(ch=='0') //当为0时,将结点置空T=NULL;else {T=(BTree)malloc(sizeof(BTree)); //分配一个新的结点T->data=ch;printf("请输入%c结点的左孩子结点:",T->data);T->lchild=CreateTree(); //通过递归建立左孩子结点printf("请输入%c结点的右孩子结点:",T->data);T->rchild=CreateTree(); //通过递归建立右孩子结点}return T;
}/*3、广义表输出二叉树*/
void ShowTree(BTree T) {if(T!=NULL) {//当二叉树不为空时printf("%c",T->data); //输入出该结点的数据域if(T->lchild!=NULL) { //若该结点的左子树不为空printf("("); //输出一个左括号ShowTree(T->lchild); //通过递归继续输出结点的左子树结点下的各结点if(T->rchild!=NULL) { //若该结点右子树不为空printf(","); //输出一个逗号ShowTree(T->rchild); //通过递归继续输出结点的右子树结点下的各结点}printf(")"); //输出一个右括号} else { //若左子树为空,右子树不为空if(T->rchild!=NULL) {printf("("); //输出一个左括号ShowTree(T->lchild); //通过递归继续输出结点的左子树结点下的各结点if(T->rchild!=NULL) { //若该结点的右子树不为空 printf(","); //输出一个逗号ShowTree(T->rchild); //通过递归继续输出结点的右子树结点下的各结点}printf(")"); //输出一个右括号}}}
}/*主函数*/
int main() {BTree T;T=NULL;printf("请输入二叉树的根结点:");T=CreateTree(); //建立二叉树printf("建立的二叉树如下:\n");ShowTree(T); //通过广义表显示二叉树
}
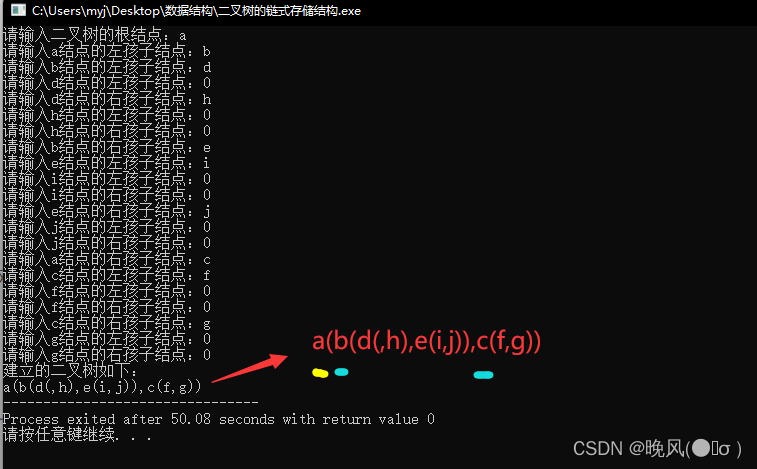
依次输入各个结点的左右孩子结点,若结点不存在则输入0,例如树中结点d的左孩子结点不存在,结点f、g、h、i、j的左右孩子都不存在,输入时都输入0。
运行结果如下,结果通过广义表的定义显示:
相关文章:

数据结构学习笔记——广义表
目录 一、广义表的定义二、广义表的表头和表尾三、广义表的深度和长度四、广义表与二叉树(一)广义表表示二叉树(二)广义表表示二叉树的代码实现 一、广义表的定义 广义表是线性表的进一步推广,是由n(n≥0&…...
)
为什么每次optimizer.zero_grad()
当你训练一个神经网络时,每一次的传播和参数更新过程可以被分解为以下步骤: 1前向传播:网络对输入数据进行操作,最终生成输出。这个过程会基于当前的参数(权重和偏差)计算出一个或多个损失函数的值。 2计…...

一个页面从输入 URL 到页面加载显示完成,这个过程中都发生了什么
一个页面从输入URL到加载显示完成经历了以下过程: DNS解析:浏览器会解析URL中的域名,将其转换为对应的IP地址。如果浏览器缓存中存在该域名的IP地址,则跳过DNS解析步骤。 建立TCP连接:通过解析得到的IP地址࿰…...

iOS ------ UICollectionView
一,UICollectionView的简介 UICollectionView是iOS6之后引入的一个新的UI控件,它和UITableView有着诸多的相似之处,其中许多代理方法都十分类似。简单来说,UICollectionView是比UITbleView更加强大的一个UI控件,有如下…...
ElasticSearch知识体系详解
1.介绍 ElasticSearch是基于Lucene的开源搜索及分析引擎,使用Java语言开发的搜索引擎库类,并作为Apache许可条款下的开放源码发布,是当前流行的企业级搜索引擎。 它可以被下面这样准确的形容: 一个分布式的实时文档存储…...

Linux自启服务提示:systemd[1]: *.service: main process exited, code=exited, status=1问题
这两天一直在沉迷于配脚本,由于服务器很多,所以我都是从一台服务器上配置好的脚本直接copy到另一台服务器,按说完全一样的脚本一样的操作,那么应该是一样的执行结果 but, Gul’dan,代…我重启服务器后服务并没有正常启…...
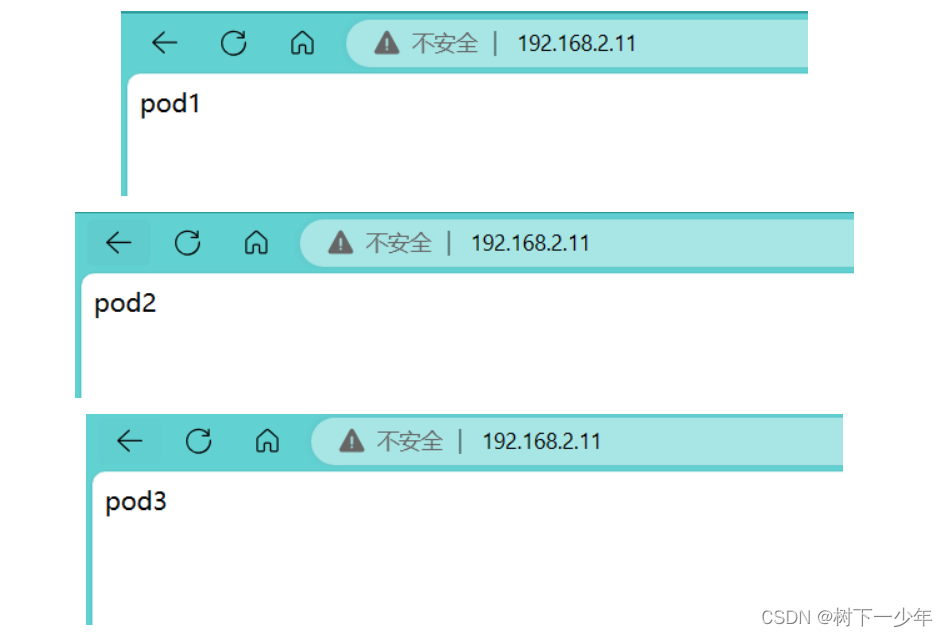
LoadBalancer将服务暴露到外部实现负载均衡purelb-layer2模式配置介绍
目录 一.purelb简介 1.简介 2.purelb的layer2工作模式特点 二.layer2的配置演示 1.首先准备ipvs和arp配置环境 2.purelb部署开始 (1)下载purelb-complete.yaml文件并应用 (2)查看该有的资源是否创建完成并运行 ÿ…...
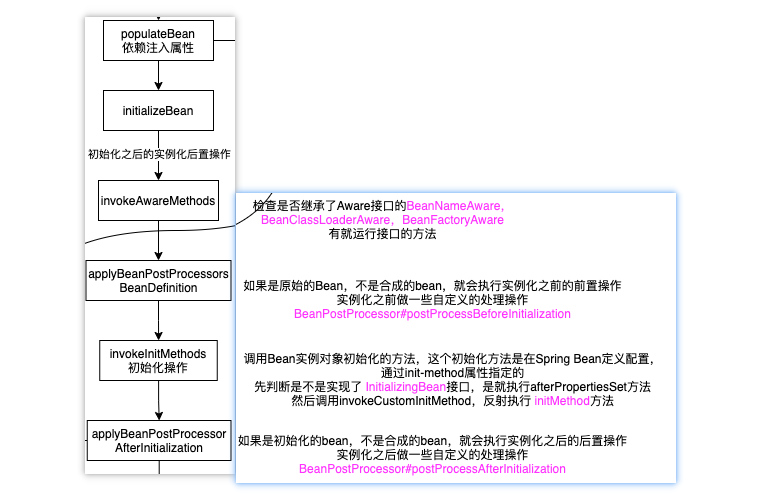
Spring Bean的生命周期各阶段详解附源码
目录 Bean的生命周期Bean定义阶段Bean实例化阶段Bean属性注入阶段Bean初始化阶段Bean销毁阶段 Bean的生命周期 bean的生命周期,我们都知道大致是分为:bean定义,bean的实例化,bean的属性注入,bean的初始化以及bean的销毁…...
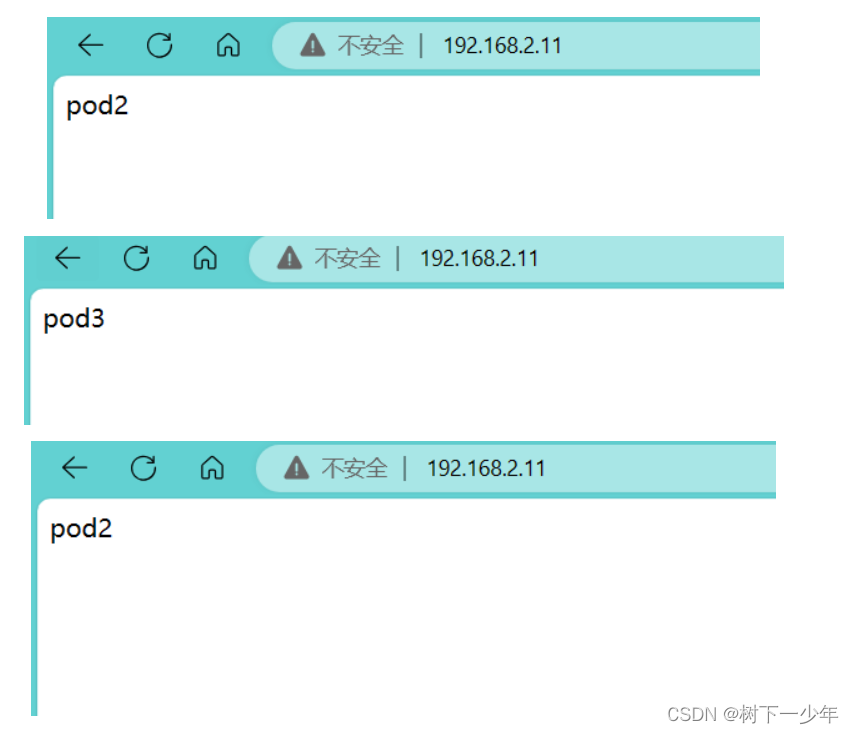
LoadBalancer将服务暴露到外部实现负载均衡Openelb-layer2模式配置介绍
目录 一.openelb简介 二.主要介绍layer2模式 1.简介 2.原理 3.部署 (1)先在集群master上开启kube-proxy的strictARP (2)应用下载openelb.yaml(需要修改镜像地址) (3)编写yam…...

Android异步之旅:探索IntentService
1.介绍IntentService IntentService是Android中的一个Service类,用于在后台执行耗时操作,而不会阻塞UI线程。它封装了HandlerThread和Handler,使得我们可以方便地在后台执行任务,而不需要自己管理线程和消息处理。 以下是 Intent…...
)
131.类型题-计算数学序列的和,请编写函数fun,其功能是S=……【满分解题代码+详细分析】(数学序列的和类型题-C/C++JavaPython实现)
文章目录 131.类型题-计算数学序列的和:计算并输出一.题目1.1 解题思路二.解题代码2.1 C/C++解题代码2.2 python解题代码2.3 Java解题代码三.解题代码仔细分析3.1 C/C++解题代码仔细分析3.2 Java解题代码仔细分析3.3 Python解题代码仔细分析四.本类型题解题诀窍五.寄语131.类型…...
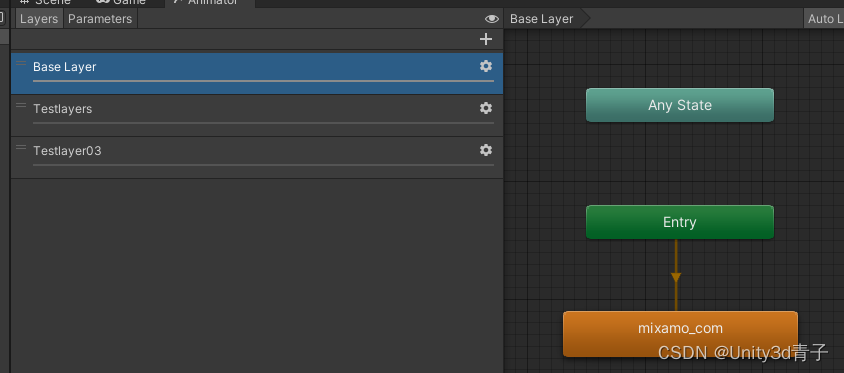
【Unity动画】状态机中层的融合原理与用法详解
1. 状态机概念介绍 在Unity中,动画状态机(Animator State Machine)是一种强大的工具,用于控制游戏对象的动画行为。动画状态机由多个动画状态Animation和过渡条件Transition、层组成!而层(Layersÿ…...

等保之道:从基础出发,解密网站防护的重要性
随着数字化时代的推进,网站安全问题日益凸显。网站被攻击不仅会导致信息泄漏、服务中断,还可能损害用户信任和企业声誉。为了更好地解决这一问题,我们需从等保的角度审视网站防护,全面提升网络安全水平。 等保背景 等保࿰…...

7. 系统信息与系统资源
7. 系统信息与系统资源 1. 系统信息1.1 系统标识 uname()1.2 sysinfo()1.3 gethostname()1.4 sysconf() 2. 时间、日期2.1 Linux 系统中的时间2.1.1 Linux 怎么记录时间2.1.2 jiffies 的引入 2.2 获取时间 time/gettimeofday2.2.1 time()2.2.2 gettimeofday() 2.3 时间转换函数…...

【重点】【滑动窗口】239. 滑动窗口最大值
题目 也可参考:剑指offer——面试题65:滑动窗口的最大值 class Solution {public int[] maxSlidingWindow(int[] nums, int k) {int[] res new int[nums.length - k 1];Deque<Integer> q new LinkedList<>();int inx 0;while (inx <…...

d3dx9_43.dll丢失原因以及5个解决方法详解
在电脑使用过程中,我们可能会遇到一些错误提示,其中之一就是“d3dx9_43.dll缺失”。这个错误提示通常表示我们的电脑上缺少了DirectX的一个组件,而DirectX是游戏和多媒体应用所必需的软件。本文将介绍d3dx9_43.dll缺失对电脑的影响以及其原因…...
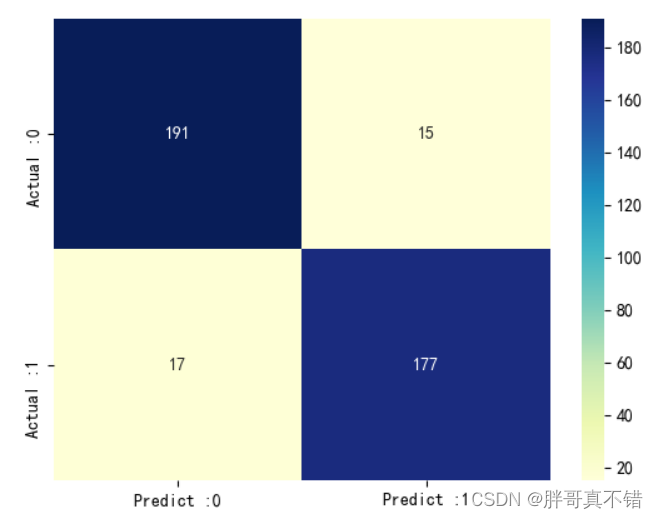
Python实现FA萤火虫优化算法优化卷积神经网络分类模型(CNN分类算法)项目实战
说明:这是一个机器学习实战项目(附带数据代码文档视频讲解),如需数据代码文档视频讲解可以直接到文章最后获取。 1.项目背景 萤火虫算法(Fire-fly algorithm,FA)由剑桥大学Yang于2009年提出 , …...

不瞒各位,不安装软件也能操作Xmind文档
大家好,我是小悟 作为搞技术的一个人群,时不时就要接收产品经理发过来的思维脑图,而此类文档往往是以Xmind编写的,如果你的电脑里面没有安装Xmind的话,不好意思,是打不开这类后缀结尾的文档。 打不开的话…...

你了解Redis 的二进制安全吗
最近面试的时候被问到Redis 的二进制安全相关八股文面试题。Redis二进制安全内容比较多,以下是简单的总结大致的过程,需要深入学习的建议跳过 Redis是基于C语言进行开发的,而C语言中的字符串是二进制不安全的,所以Redis就没有直接…...
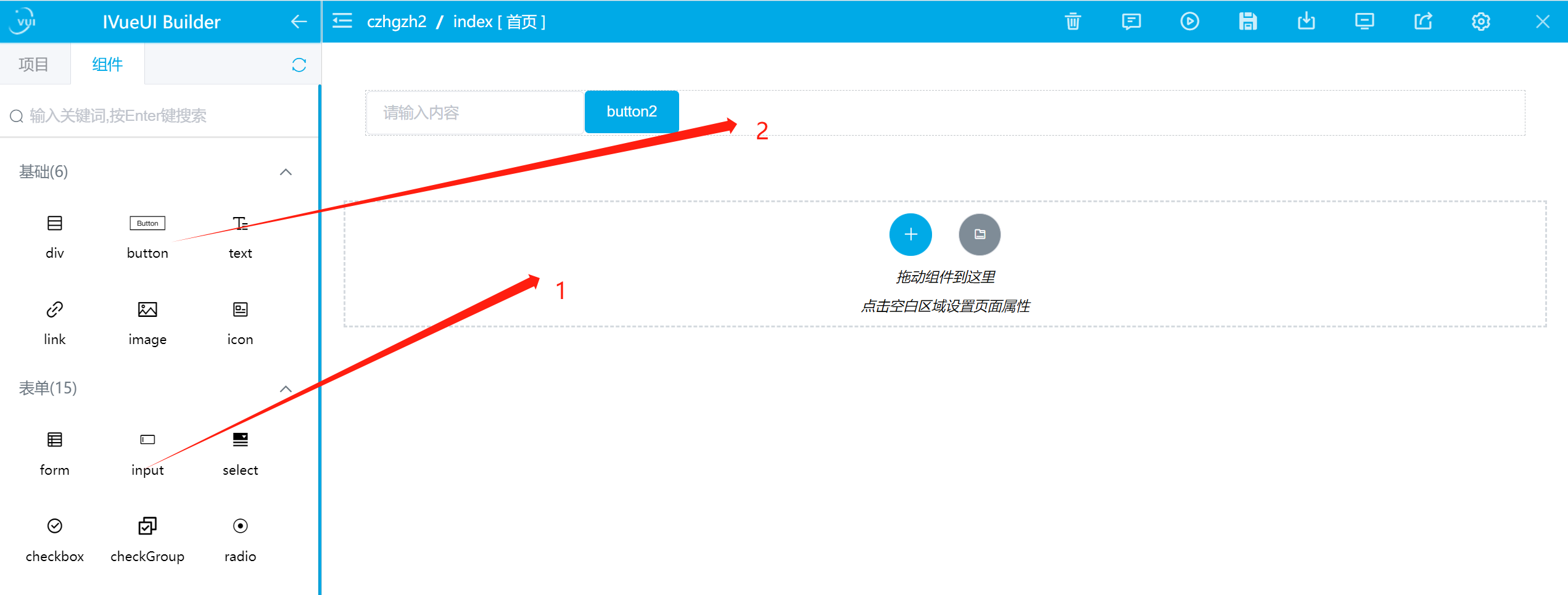
探索前端设计的新境界——介绍IVueUI工具助力Vue页面设计
在快速发展的前端领域,Vue.js作为一款渐进式JavaScript框架,一直备受开发者喜爱。然而,在Vue前端开发的旅程中,页面设计常常是一个不可避免的挑战。今天,我要向大家介绍一款令Vue前端开发者受益匪浅的工具——www.ivue…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程(限时至2025/5/15) Oracle AI Vector Search 1Z0-184-25考试,都顺利拿到certified了没。 各行各业的AI 大模型的到来,传统的数据库中的SQL还能不能打,结构化和非结构的话数据如何和…...
