【爬虫逆向分析实战】某笔登录算法分析——本地替换分析法
前言
作者最近在做一个收集粉币的项目,可以用来干嘛这里就不展开了😁,需要进行登录换算token从而达到监控收集的作用,手机抓包发现他是通过APP进行计算之后再请求接口的,通过官网分析可能要比APP逆向方便多,但是通过这几天的观察我并没有头绪,这篇文章草稿创建了接近一个月了,无从下笔,借助了人工智能也没有达到效果,可见它的难度不一般(也可能是我JS基础太过薄弱的原因),本次我们用一种分析方法慢慢的瓦解击破他的层层逻辑!
JS启动分析
这里从网站入手,原因如下:
没有验证码JS结构清晰
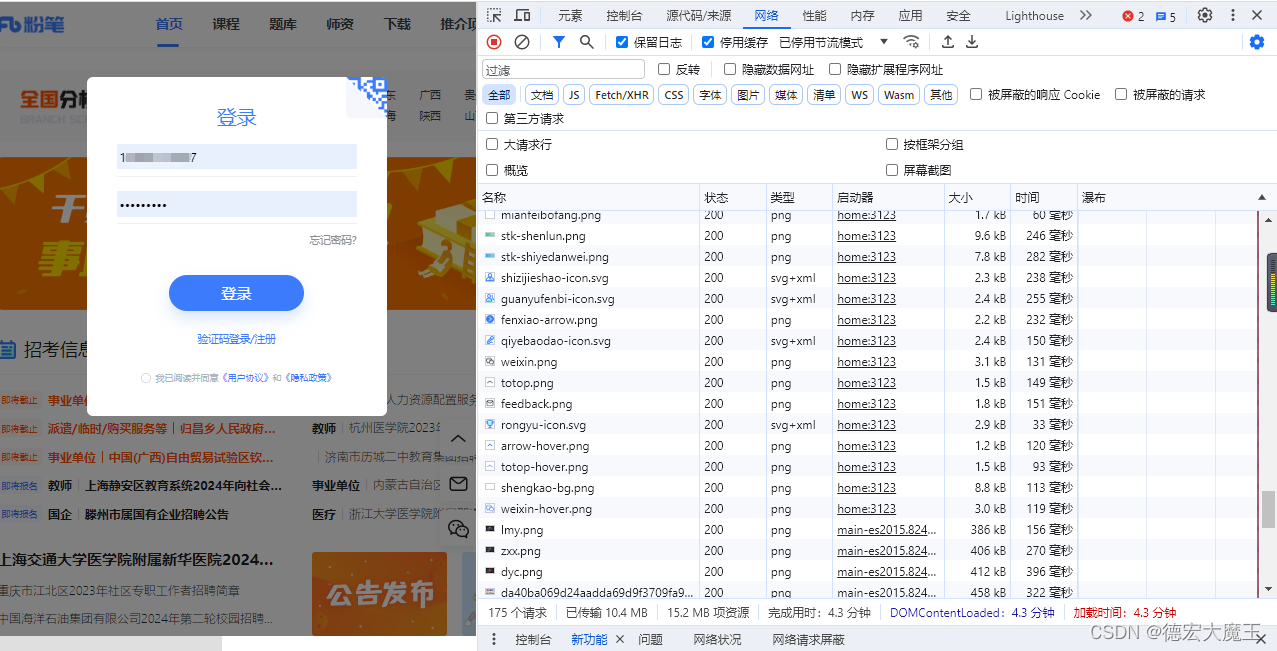
观察不难发现,密码是被加密的
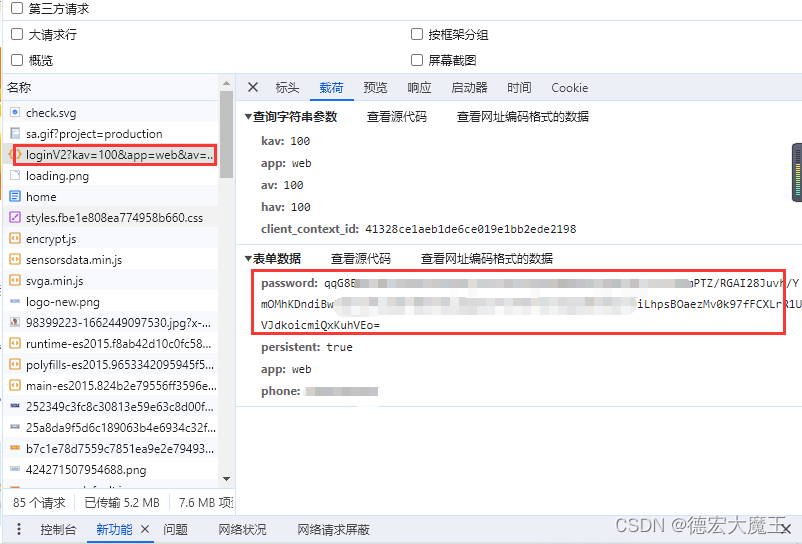
必定是通过js进行加密的,我们查看启动器

发现有以下几个关键JS
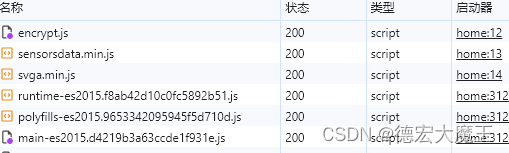
第一感觉是,main为主方法,其他的是用来调用的,encrypt应该是用于加密的方法,通过上面的启动器证实了main.js的确是优先启动的
找到main.js搜索password
密码通过this.encrypt()进行加密的
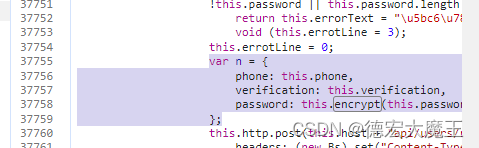
var n = {
phone: this.phone,
verification: this.verification,
password: this.encrypt(this.password)
};
找到encrypt()方法
encrypt(n) {
return window.encrypt(this.publicKey, n)
}
需要用到一个参数publicKey
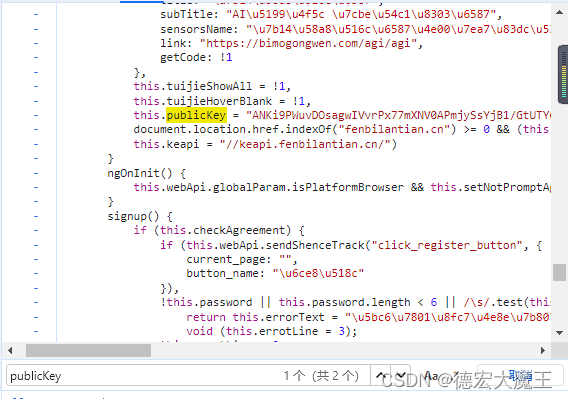
到这里我们基本搞清楚了,登录时将原密码,进行调用window.encrypt(this.publicKey, n)加密
猜想
猜测n为原密码,如何证实呢?有很多人想说观察代码的调用,这当然可以,但如果是复杂的代码或者加密的你还能看吗?
这里用了一个浏览器自带的功能本地替换,可以无视代码加密,为什么这么说,因为代码加密最后还是要被执行,不能执行的代码加密了有啥用呢??
我们找到main.js将n弹窗显示
encrypt(n) {alert(n);return encrypt(this.publicKey, n)}
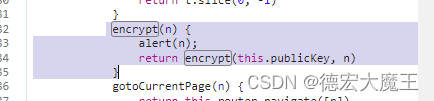
替换到本地启用后,我们进行登录模拟,看看有没有效果?
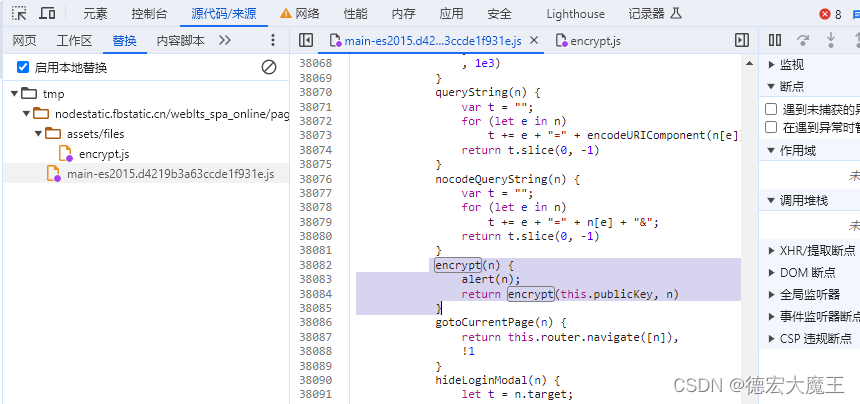
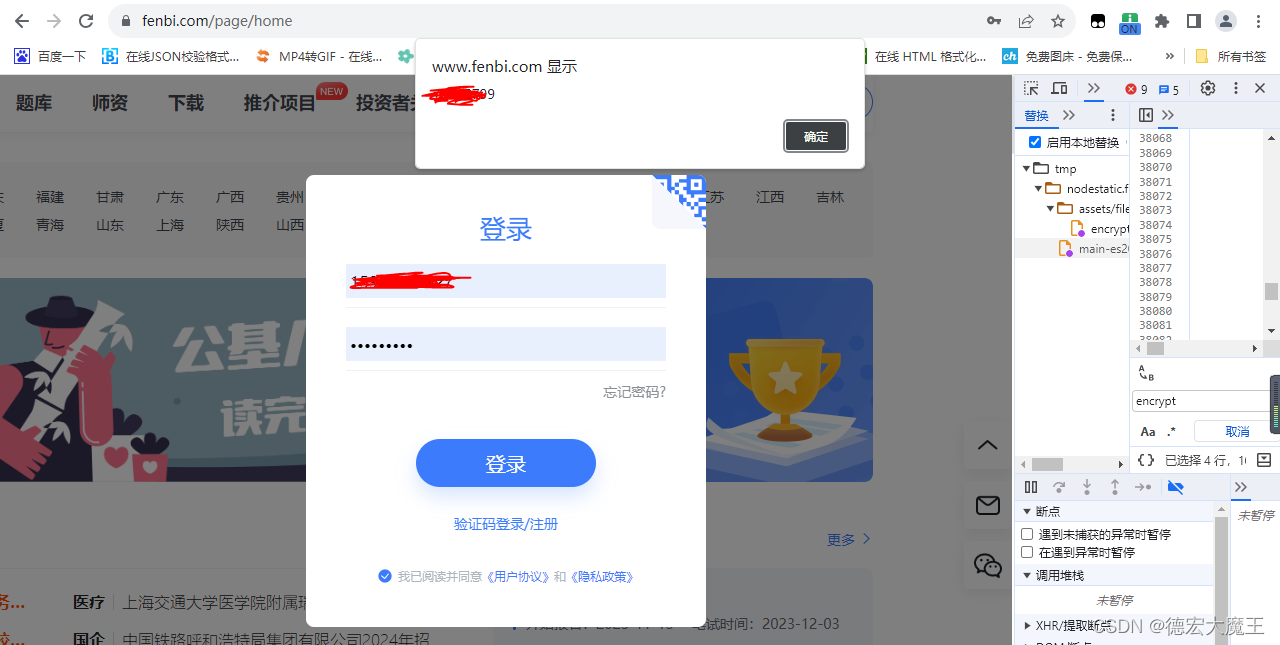
这里将我的登录密码弹出来了,猜想正确!
顺藤摸瓜
有了刚刚的思想,我们直接找encrypt.js,因为在main.js中最后调用了
return encrypt(this.publicKey, n)
而在main.js中没有其他方法了 ,在encrypt.js我们找到了相关方法
av.encrypt = function(aG, z) {var t = new N();t.setPublic(a(aG), "10001");return ai(t.encrypt(z))}
代码是否运行到这里,和刚刚一样验证一下就可以了

发现又调用了新的方法ai(t.encrypt(z))
function ai(aG) {var z;var aH;var t = "";for (z = 0; z + 3 <= aG.length; z += 3) {aH = parseInt(aG.substring(z, z + 3), 16);t += ad.charAt(aH >> 6) + ad.charAt(aH & 63)}if (z + 1 == aG.length) {aH = parseInt(aG.substring(z, z + 1), 16);t += ad.charAt(aH << 2)} else {if (z + 2 == aG.length) {aH = parseInt(aG.substring(z, z + 2), 16);t += ad.charAt(aH >> 2) + ad.charAt((aH & 3) << 4)}}while ((t.length & 3) > 0) {t += Y}alert(t);return t}
我们在修改代码将t进行弹窗显示,重新来一遍整个登录过程,观察最后的加密密码是否与请求的一致
模拟登录测试
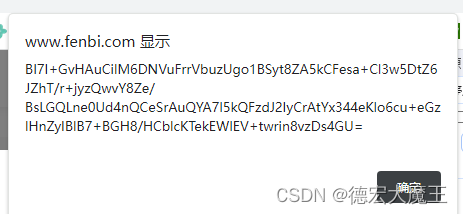
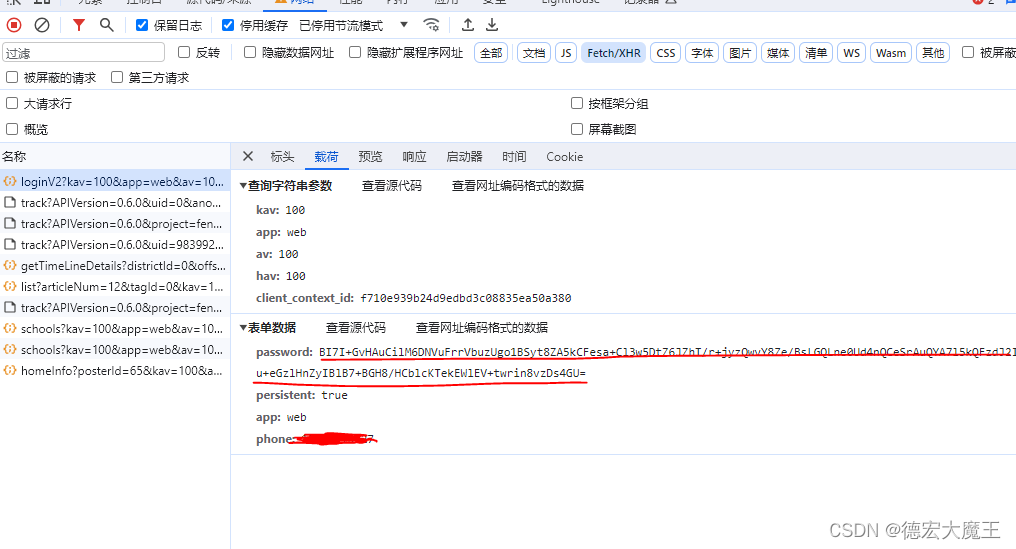
经过对比是一致的,由于我们的环境是python,接下来借助GPT进行代码转换
代码转换
通过将涉及到的函数调用方法进行罗列,通过人工智能改写
var publicKey='ANKi9PWuvDOsagwIVvrPx77mXNV0APmjySsYjB1/GtUTY6cyKNRl2RCTt608m9nYk5VeCG2EAZRQmQNQTyfZkw0Uo+MytAkjj17BXOpY4o6+BToi7rRKfTGl6J60/XBZcGSzN1XVZ80ElSjaGE8Ocg8wbPN18tbmsy761zN5S';
var n='密码'
encrypt(publicKey, n)encrypt(aG, z) {var t = new N();t.setPublic(a(aG), "10001");return ai(t.encrypt(z))}function a(aI) {alert("经过");var aG = "";var aH;var t = 0;var z;for (aH = 0; aH < aI.length; ++aH) {if (aI.charAt(aH) == Y) {break}v = ad.indexOf(aI.charAt(aH));if (v < 0) {continue}if (t == 0) {aG += aF(v >> 2);z = v & 3;t = 1} else {if (t == 1) {aG += aF((z << 2) | (v >> 4));z = v & 15;t = 2} else {if (t == 2) {aG += aF(z);aG += aF(v >> 2);z = v & 3;t = 3} else {aG += aF((z << 2) | (v >> 4));aG += aF(v & 15);t = 0}}}}if (t == 1) {aG += aF(z << 2)}return aG}function ai(aG) {// alert(aG);var z;var aH;var t = "";for (z = 0; z + 3 <= aG.length; z += 3) {aH = parseInt(aG.substring(z, z + 3), 16);t += ad.charAt(aH >> 6) + ad.charAt(aH & 63)}if (z + 1 == aG.length) {aH = parseInt(aG.substring(z, z + 1), 16);t += ad.charAt(aH << 2)} else {if (z + 2 == aG.length) {aH = parseInt(aG.substring(z, z + 2), 16);t += ad.charAt(aH >> 2) + ad.charAt((aH & 3) << 4)}}while ((t.length & 3) > 0) {t += Y}alert(t);return t}
相关文章:

【爬虫逆向分析实战】某笔登录算法分析——本地替换分析法
前言 作者最近在做一个收集粉币的项目,可以用来干嘛这里就不展开了😁,需要进行登录换算token从而达到监控收集的作用,手机抓包发现他是通过APP进行计算之后再请求接口的,通过官网分析可能要比APP逆向方便多࿰…...

vue3使用动态component
使用场景: 多个组件通过component标签挂载在同一个组件中,通过触发时间进行动态切换。vue3与vue2用法不一样,这里有坑! 使用方法: 1.通过vue的defineAsyncComponent实现挂载组件 2.component中的is属性 父组件&am…...

单机游戏推荐:巨击大乱斗 GIGABASH 中文安装版
在泰坦之中称霸天下吧!《GigaBash 巨击大乱斗》是一款多人战斗擂台游戏,有着受特摄片启发的巨型怪兽,具有传奇色彩的英雄,震天动地的特别攻击,以及可以完全摧毁的擂台场景。 游戏特点 怪物大解放 多达10个独特的角…...

计算机系统启动过程
计算机系统启动过程 阅读笔记: 《计算机体系结构基础(第三版)》-- 胡伟武 第7章:计算机系统启动过程分析 系统启动的整个过程中, 计算机系统在软件的控制下由无序到有序, 所有的组成部分都由程序管理, 按照程序的执行发挥各自的功…...

DedeCms后台文章列表文档id吗?或者快速定位id编辑文章
我们在建站时有的时候发现之前的文章有错误了,要进行修改,但又不知道文章名,只知道大概的文章id,那么可以搜索到DedeCms后台文章列表文档id吗?或者快速定位文章id方便修改? 第一种方法:复制下面…...
【开发问题解决方法记录】03.dian
登录提示 ERR-1002 在应用程序 "304" 中未找到项 "ROLE_ID" 的项 ID。 一开始找错方向了,以为是代码错误,但是后来在蒋老师的提醒下在共享组件-应用程序项 中发现设的项不是ROLE_ID而是ROLEID,怪不得找不到ORZ 解决方法…...

QT之QString
QT之QString 添加容器 点击栅格布局 添加容器,进行栅格布局 布局总结:每一个模块放在一个Group中,排放完之后,进行栅格布局。多个Group进行并排时,先将各个模块进行栅格布局,然后都选中进行垂直布…...

常见的几种计算机编码格式
前言: 计算机编码是指将字符、数字和符号等信息转换为计算机可识别的二进制数的过程,正因如此,计算机才能识别中英文等各类字符。计算机中有多种编码格式用于表示和存储文本、字符和数据,实际走到最后都是二进制,本质一…...

3D旋转tab图
上图 代码 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>3D旋转tab图</title><style>* {margin: 0;padding: 0;}body {height: 100vh;background: linear-gradient(to top, #29323c, #…...

openGL 三:矩阵和向量
1.使用glm数学库进行矩阵和向量的计算 2.位置坐标可以看做一个向量 3.向量的移动,缩放,旋转,都是可以通过和矩阵的计算得出 4.向量的缩放乘一个44的矩阵 5.注意事项(有些版本的glm::mat4 不是默认构建一个单位44的矩阵)…...
Socket和Http的通讯原理,遇到攻击会受到哪些影响以及如何解决攻击问题。
德迅云安全-领先云安全服务与解决方案提供商 Socket和HTTP通信原理: Socket通信原理: Socket是一种应用程序编程接口(API),用于在单个进程或多个进程之间进行通信。它提供了一种灵活的、异步的通信方式,使…...
【springboot】整合redis
1.前提条件:docker安装好了redis确定redis可以访问 可选软件: 2.测试代码 (1)redis依赖 org.springframework.boot spring-boot-starter-data-redis (2)配置redis (3) 注入 Resource StringRedisTemplate stringRedisTemplate; 对键进行操作 –o…...

回溯和分支算法
状态空间图 “图”——状态空间图 例子:农夫过河问题——“图”状态操作例子:n后问题、0-1背包问题、货郎问题(TSP) 用向量表示解,“图”由解向量扩张得到的解空间树。 ——三种图:n叉树、子集树、排序树 剪枝 不满住条件的…...

深入理解:指针变量的解引用 与 加法运算
前言 指针变量的解引用和加法运算是非常高频的考点,也是难点,因为对初学者的不友好,这就导致了各大考试都很喜欢在这里出题,通常会伴随着强制类型转换、二维数组、数组指针等一起考查大家对指针的理解。但是不要怕,也许…...

Docker 镜像构建的最佳做法
一、镜像分层 使用docker image history命令,可以看到用于在镜像中创建每个层的命令。 1、 使用docker image history命令查看创建的入门镜像中的层。 docker image history getting-started 您应该得到如下所示的输出: IMAGE CREATED…...
工作上Redis安装及配置
下载redis软件 第一步:解压压缩包 tar -zxvf redis-7.0.14.tar.gz 第二步:移动redis存放目录(结合个人需求而定!) redis-7.0.14:解压后的文件路径 /usr/local:移动后的文件路径 mv redis-7.0.…...

电商项目之Web实时消息推送(附源码)
文章目录 1 问题背景2 前言3 什么是消息推送4 短轮询5 长轮询5.1 demo代码 6 iframe流6.1 demo代码 7 SSE7.1 demo代码7.2 生产环境的应用 (重要) 8 MQTT 1 问题背景 扩宽自己的知识广度,研究一下web实时消息推送 2 前言 文章参考自Web 实时消…...

上机实验四 哈希表设计 西安石油大学数据结构
实验名称:哈希表设计 (1)实验目的:掌握哈希表的设计方法及其冲突解决方法。 (2)主要内容: 已知一个含有10个学生信息的数据表,关键字为学生“姓名”的拼音,给出此表的一…...

Ubuntu22.04 交叉编译mp4V2 for Rv1106
一、配置工具链环境 sudo vim ~/.bashrc在文件最后添加 export PATH$PATH:/opt/arm-rockchip830-linux-uclibcgnueabihf/bin 保存,重启机器 二、下载mp4v2 下载路径:MP4v2 | mp4v2 三、修改CMakeLists.txt 四、执行编译 mkdir build cd buildcmak…...
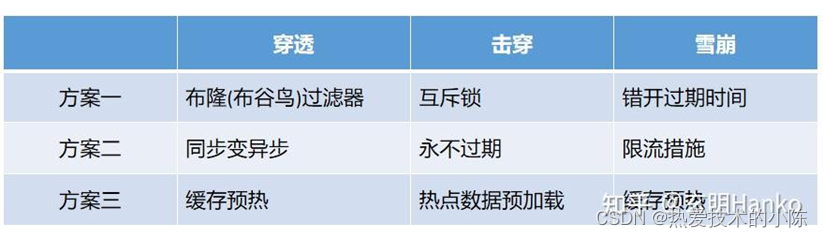
缓存穿透、击穿、雪崩
缓存穿透: 指的是恶意用户或攻击者通过请求不存在于缓存和后端存储中的数据来使得所有请求都落到后端存储上,导致系统瘫痪。 解决方案: 通常包括使用布隆过滤器或者黑白名单等方式来过滤掉无效请求,以及在应用程序中加入缓存预热…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...
