【Docker】从零开始:13.Docker安装tomcat
Docker】从零开始:13.Docker安装Tomcat
- 下载Tomcat镜像
- 启动Tomcat镜像
- 新版本Tomcat修改
- 访问Tomact首页
下载Tomcat镜像
[root@docker ~]# docker pull tomcat
Using default tag: latest
latest: Pulling from library/tomcat
0e29546d541c: Pull complete
9b829c73b52b: Pull complete
cb5b7ae36172: Pull complete
6494e4811622: Pull complete
668f6fcc5fa5: Pull complete
dc120c3e0290: Pull complete
8f7c0eebb7b1: Pull complete
77b694f83996: Pull complete
0f611256ec3a: Pull complete
4f25def12f23: Pull complete
Digest: sha256:9dee185c3b161cdfede1f5e35e8b56ebc9de88ed3a79526939701f3537a52324
Status: Downloaded newer image for tomcat:latest
docker.io/library/tomcat:latest
[root@docker ~]# docker images
REPOSITORY TAG IMAGE ID CREATED SIZE
tomcat latest fb5657adc892 23 months ago 680MB
[root@docker ~]#
启动Tomcat镜像
[root@docker ~]# docker run -d -p8080:8080 --name tomcat tomcat
3b44ad54e93b0a0c0b7d4c92bfdcce8c9189efae8bfbaf6f0701545bac2f6b07
[root@docker ~]# docker ps
CONTAINER ID IMAGE COMMAND CREATED STATUS PORTS NAMES
3b44ad54e93b tomcat "catalina.sh run" 9 seconds ago Up 8 seconds 0.0.0.0:8080->8080/tcp, :::8080->8080/tcp tomcat
[root@docker ~]#
新版本Tomcat修改
- 新版本Tomcat webapps为空 原webapps目录移动至 webapps.dist下,所以我们要进行处理
[root@docker ~]# docker exec -it 3b44ad54e93b /bin/bash
root@3b44ad54e93b:/usr/local/tomcat# ls -l
total 132
-rw-r--r--. 1 root root 18994 Dec 2 2021 BUILDING.txt
-rw-r--r--. 1 root root 6210 Dec 2 2021 CONTRIBUTING.md
-rw-r--r--. 1 root root 60269 Dec 2 2021 LICENSE
-rw-r--r--. 1 root root 2333 Dec 2 2021 NOTICE
-rw-r--r--. 1 root root 3378 Dec 2 2021 README.md
-rw-r--r--. 1 root root 6905 Dec 2 2021 RELEASE-NOTES
-rw-r--r--. 1 root root 16517 Dec 2 2021 RUNNING.txt
drwxr-xr-x. 2 root root 4096 Dec 22 2021 bin
drwxr-xr-x. 1 root root 22 Dec 5 04:55 conf
drwxr-xr-x. 2 root root 4096 Dec 22 2021 lib
drwxrwxrwx. 1 root root 80 Dec 5 04:55 logs
drwxr-xr-x. 2 root root 159 Dec 22 2021 native-jni-lib
drwxrwxrwx. 2 root root 30 Dec 22 2021 temp
drwxr-xr-x. 2 root root 6 Dec 22 2021 webapps
drwxr-xr-x. 7 root root 81 Dec 2 2021 webapps.dist
drwxrwxrwx. 2 root root 6 Dec 2 2021 work
root@3b44ad54e93b:/usr/local/tomcat# rm -rf webapps
root@3b44ad54e93b:/usr/local/tomcat# mv webapps.dist webapps
root@3b44ad54e93b:/usr/local/tomcat# 访问Tomact首页
相关文章:

【Docker】从零开始:13.Docker安装tomcat
Docker】从零开始:13.Docker安装Tomcat 下载Tomcat镜像启动Tomcat镜像新版本Tomcat修改访问Tomact首页 下载Tomcat镜像 [rootdocker ~]# docker pull tomcat Using default tag: latest latest: Pulling from library/tomcat 0e29546d541c: Pull complete 9b829c7…...
:Java 动态脚本)
风控规则引擎(一):Java 动态脚本
风控规则引擎(一):Java 动态脚本 日常场景 共享单车会根据微信分或者芝麻分来判断是否交押金汽车租赁公司也会根据微信分或者芝麻分来判断是否交押金在一些外卖 APP 都会提供根据你的信用等级来发放贷款产品金融 APP 中会根据很复杂规则来判…...

第五十六天|583. 两个字符串的删除操作 72. 编辑距离
583. 两个字符串的删除操作 可以求出最大子序列然后用字符串长度去减,也可以用删除的思路,如下: class Solution { public:int minDistance(string word1, string word2) {vector<vector<int>> dp(word1.size()1,vector<int…...

java中Lists.newArrayList和new ArrayList的详细区别?
下面是对Lists.newArrayList()和new ArrayList<>()的详细区别进行举例说明: 创建具有初始数据的列表: java Copy code import com.google.common.collect.Lists; List<String> list1 Lists.newArrayList("apple", "banana…...
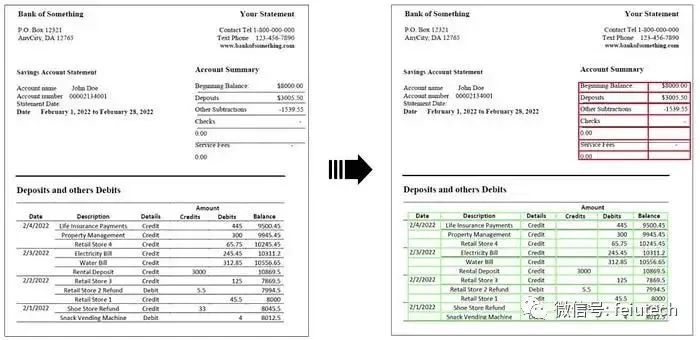
从图片或PDF文件识别表格提取内容的简单库img2table
img2table是一个基于OpenCV 图像处理的用于 PDF 和图像的表识别和提取 Python库。由于其设计基于神经网络的解决方案,提供了一种实用且更轻便的替代方案,尤其是在 CPU 上使用时。 该库的特点: 识别图像和PDF文件中的表格,包括在表…...

CSV文件中使用insert 函数在指定列循环插入不同数据
文章目录 一、系统、工具要求二、需求三、代码实现:四、核心代码解读五、逐行更改某一列数据六:实现在文件的末尾增加指定内容列 一、系统、工具要求 pandaspythoncsv Windows 系统 二、需求 我有两个文件: 文件一:subject_ma…...
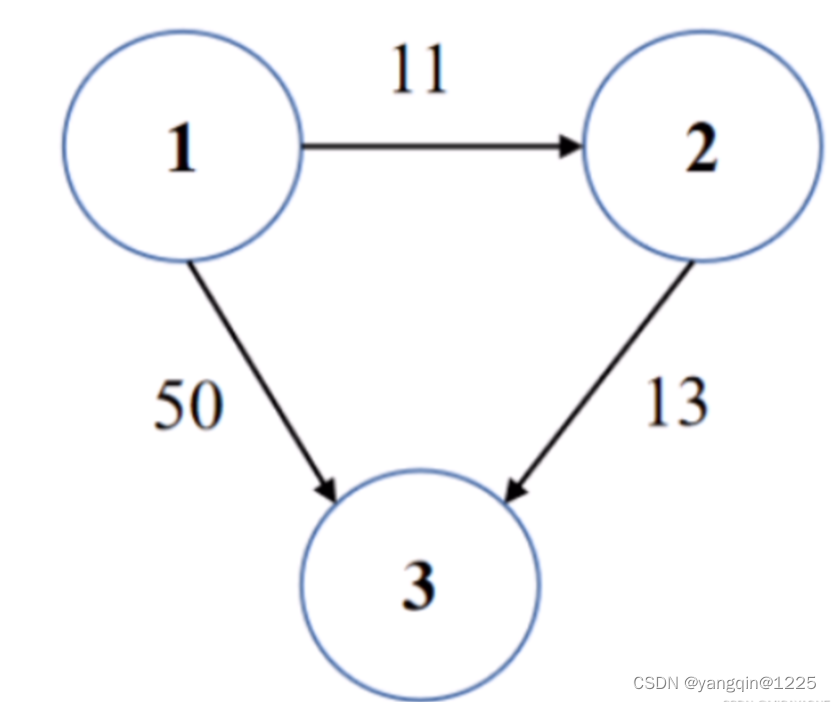
【华为OD题库-064】最小传输时延I-java
题目 某通信网络中有N个网络结点,用1到N进行标识。网络通过一个有向无环图.表示,其中图的边的值表示结点之间的消息传递时延。 现给定相连节点之间的时延列表times[]{u,v, w),其中u表示源结点,v表示目的结点࿰…...
全文检索[ES系列] - 第495篇
历史文章(文章累计490) 《国内最全的Spring Boot系列之一》 《国内最全的Spring Boot系列之二》 《国内最全的Spring Boot系列之三》 《国内最全的Spring Boot系列之四》 《国内最全的Spring Boot系列之五》 《国内最全的Spring Boot系列之六》 M…...

【预计IEEE出版|EI征稿通知】第六届下一代数据驱动网络国际学术会议 (NGDN 2024)
第六届下一代数据驱动网络国际学术会议 (NGDN 2024) The Sixth International Conference on Next Generation Data-driven Networks 2024年4月26-28日 | 中国沈阳 基于前几届在英国埃克塞特 (ISPA 2020) 、中国沈阳 (TrustCom 2021) 和中国武汉 (IEEETrustCom-2022) 成功举…...

C++软件在Win平台运行总结
Windows平台: 1.需要安装运行库:无论是exe还是动态库用的哪种平台工具集(visual2010-visual2019)进行编译,需要安装对应的运行时库vc_redist.x64.exe/vc_redist.x86.exe。比如Exe用的是VisualStdio2010工具集编译,其中链接的一个…...
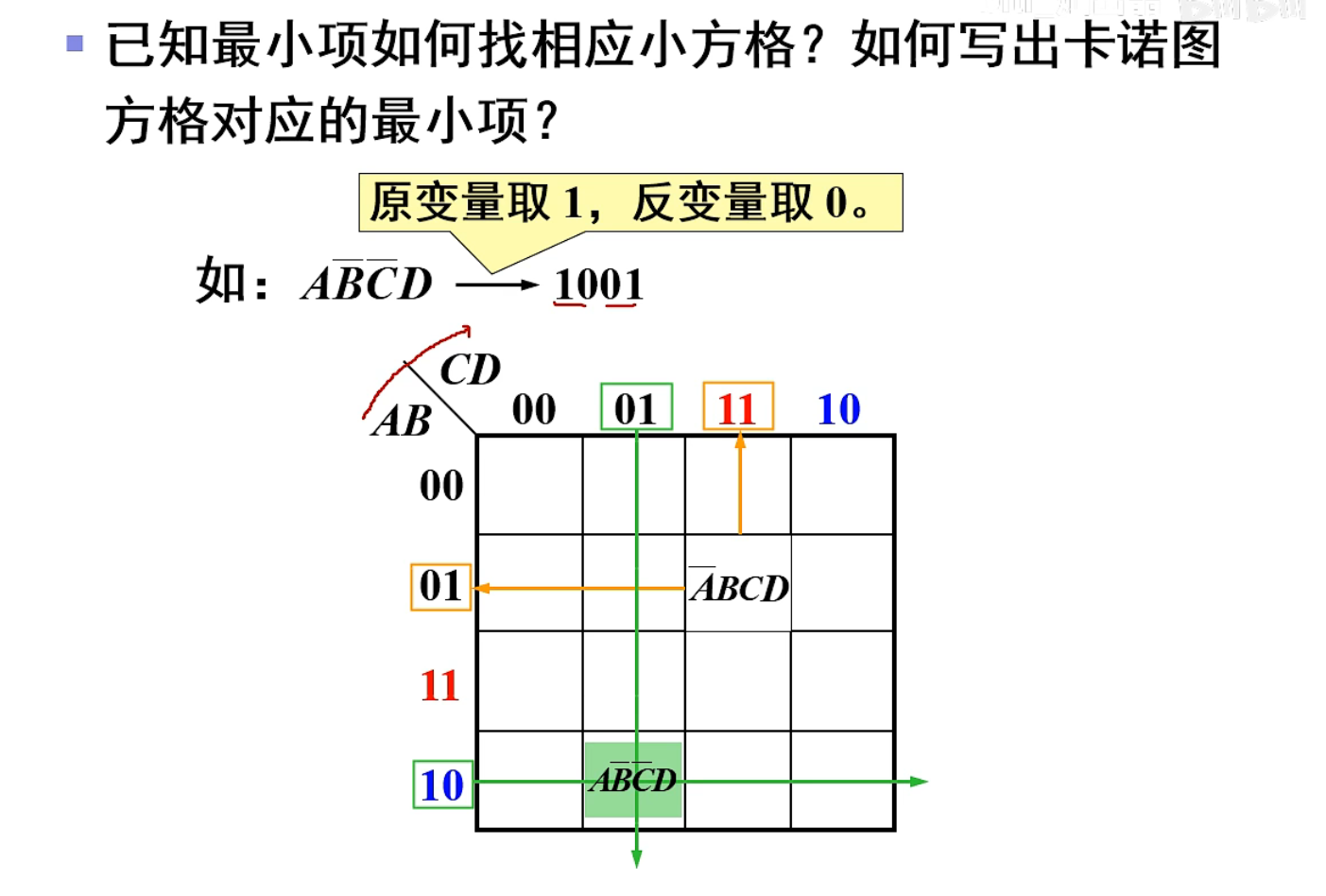
【数电笔记】16-卡诺图绘制(逻辑函数的卡诺图化简)
目录 说明: 最小项卡诺图的组成 1. 相邻最小项 2. 卡诺图的组成 2.1 二变量卡诺图 2.2 三表变量卡诺图 2.3 四变量卡诺图 3. 卡诺图中的相邻项(几何相邻) 说明: 笔记配套视频来源:B站;本系列笔记并…...
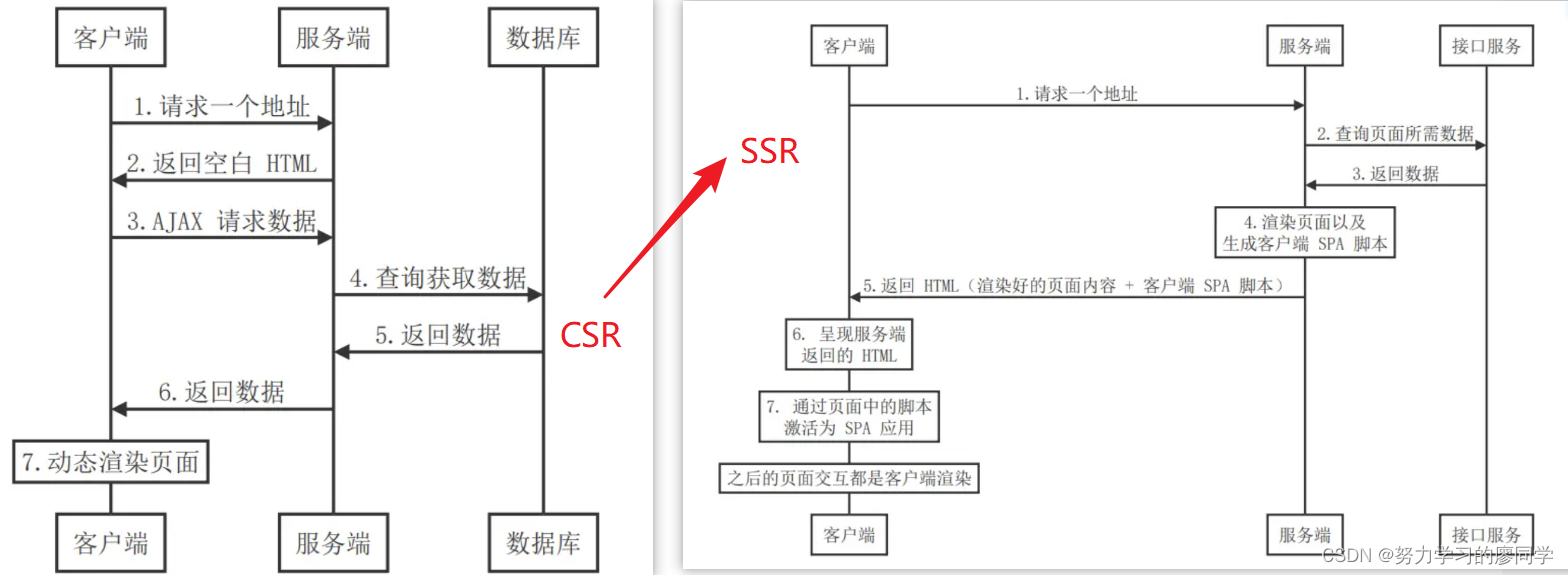
前端面试灵魂提问(1)
1.自我介绍 2.在实习中,你负责那一模块 3.any与unknow的异同 相同点:any和unkonwn 可以接受任何值 不同点:any会丢掉类型限制,可以用any 类型的变量随意做任何事情。unknown 变量会强制执行类型检查,所以在使用一个…...
Linux中项目部署步骤
安装jdk,tomcat 安装步骤 1,将压缩包,拷贝到虚拟机中。 通过工具,将文件直接拖到虚拟机的/home下 2,回到虚拟机中,查看/home下,有两个压缩文件 3,给压缩文件做解压缩操作 tar -z…...

cmd下查看python命令的用法
在cmd下,可以运行python --help或者py --help来查看python命令的用法。例如:...
)
大型语言模型在实体关系提取中的应用探索(二)
上一篇文章我们探讨了如何使用大语言模型进行实体关系的抽取。本篇文章我们将进一步探索这个话题。比较一下国内外几款知名大模型在相同的实体关系提取任务下的表现。由于精力有限,我们无法全面测试各模型的实体关系抽取能力,因此,看到的效果…...

Easy Excel设置表格样式
1. 设置通用样式 import com.alibaba.excel.annotation.ExcelProperty; import com.alibaba.excel.annotation.write.style.*; import com.fasterxml.jackson.annotation.JsonFormat; import com.xxx.npi.config.easypoi.EasyExcelDateConverter; import lombok.Data; import …...
HarmonyOS/OpenHarmony应用开发
OpenHarmony是由开放原子开源基金会(OpenAtom Foundation)孵化及运营的开源项目, 目标是面向全场景、全连接、全智能时代, 搭建一个智能终端设备操作系统的框架和平台, 促进万物互联产业的繁荣发展。 了解OpenHarmony HarmonyOS是华为通过OpenHarmony项目,结合商业…...
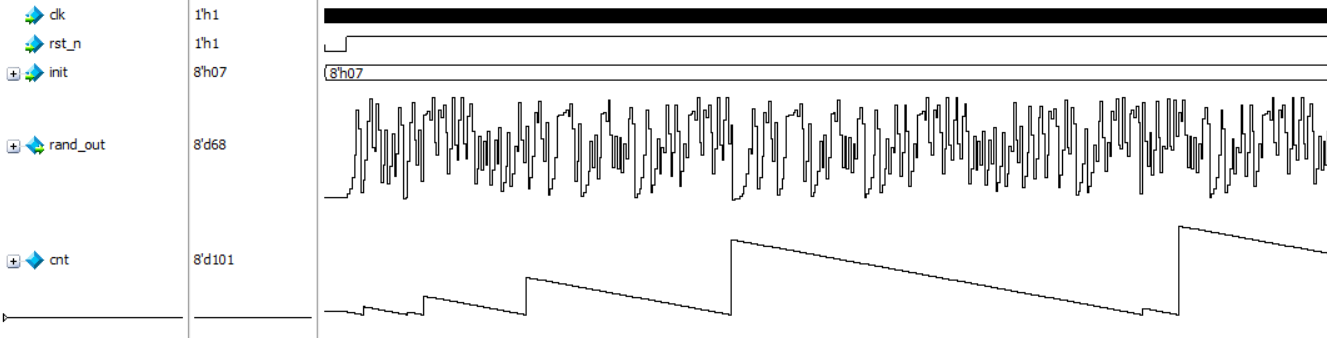
孩子都能学会的FPGA:第二十一课——用线性反馈移位寄存器实现伪随机序列
(原创声明:该文是作者的原创,面向对象是FPGA入门者,后续会有进阶的高级教程。宗旨是让每个想做FPGA的人轻松入门,作者不光让大家知其然,还要让大家知其所以然!每个工程作者都搭建了全自动化的仿…...

国内 AI 成图第一案!你来你会怎么判?
我国目前并未出台专门针对网络爬虫技术的法律规范,但在司法实践中,相关判决已屡见不鲜,K 哥特设了“K哥爬虫普法”专栏,本栏目通过对真实案例的分析,旨在提高广大爬虫工程师的法律意识,知晓如何合法合规利用…...

快速登录界面关于如何登录以及多账号列表解析以及config配置文件是如何读取(1)
快速登录界面关于如何登录以及多账号列表解析以及config配置文件是如何读取 1、快速登录界面关于如何登录以及快速登录界面账号如何显示 如图所示:根据按下按钮一键登录中途会发生什么。 关于一键登录按钮皮肤skin的设置: <Button name"QuickLoginOkBtn" text&q…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...

Java 与 MySQL 性能优化:MySQL 慢 SQL 诊断与分析方法详解
文章目录 一、开启慢查询日志,定位耗时SQL1.1 查看慢查询日志是否开启1.2 临时开启慢查询日志1.3 永久开启慢查询日志1.4 分析慢查询日志 二、使用EXPLAIN分析SQL执行计划2.1 EXPLAIN的基本使用2.2 EXPLAIN分析案例2.3 根据EXPLAIN结果优化SQL 三、使用SHOW PROFILE…...

深入理解 React 样式方案
React 的样式方案较多,在应用开发初期,开发者需要根据项目业务具体情况选择对应样式方案。React 样式方案主要有: 1. 内联样式 2. module css 3. css in js 4. tailwind css 这些方案中,均有各自的优势和缺点。 1. 方案优劣势 1. 内联样式: 简单直观,适合动态样式和…...

Python打卡训练营学习记录Day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

触发DMA传输错误中断问题排查
在STM32项目中,集成BLE模块后触发DMA传输错误中断(DMA2_Stream1_IRQHandler进入错误流程),但单独运行BLE模块时正常,表明问题可能源于原有线程与BLE模块的交互冲突。以下是逐步排查与解决方案: 一、问题根源…...

Monorepo架构: 项目管理模式对比与考量
关于 monorepo 相关概念及项目管理模式 在软件开发中,尤其是前端项目,我们会涉及到不同的项目管理模式,这里先介绍几个重要的概念“monorepo”是当前较为热门的一种项目管理方式,虽然很多人可能听说过,但可能在实际项…...

OD 算法题 B卷【删除字符串中出现次数最少的字符】
文章目录 删除字符串中出现次数最少的字符 删除字符串中出现次数最少的字符 实现删除字符串中出现次数最少的字符,若(最少的)有多个字符出现次数一样,则都删除。输出删除后的字符串,其他字符保持原有顺序;…...
)
vue-14(使用 ‘router.push‘ 和 ‘router.replace‘ 进行编程导航)
使用 ‘router.push’ 和 ‘router.replace’ 进行编程导航 编程导航是使用 Vue Router 构建动态和交互式 Web 应用程序的一个重要方面。它允许您根据应用程序逻辑、用户作或特定条件控制用户的导航流。您可以使用 router.push 和 router.replace 方法以编程方式导航到不同的路…...
