[Rust] 可迭代类型, 迭代器, 如何正确的创建自定义可迭代类型
在 Rust 中, for 语句的执行依赖于类型对于 IntoIterator 的实现, 如果某类型实现了这个 trait, 那么它就可以直接使用 for 进行循环.
直接实现
在 Rust 中, 如果一个类型实现了 Iterator, 那么它会被同时实现 IntoIterator, 具体逻辑是返回自身, 因为自身就是迭代器.
但是如果自身就是迭代器的话, 就意味着自身必须存储迭代状态, 例如当前迭代的位置. 如果是这样的话, 迭代器就只能被使用一次. 况且自身直接被传入 into_iter 方法后, 所有权被转移, 该对象就无法被再次使用了.
定义类型本身:
struct IntRange {current: i32,step: i32,end: i32
}
直接为其实现迭代器:
impl Iterator for IntRange {type Item = i32;fn next(&mut self) -> Option<Self::Item> {if self.current == self.end {return None;} else {let current = self.current;self.current += self.step;return Some(current);}}
}
使用该类型:
let range = IntRange { current: 0, step: 1, end: 10 };
for value in range {println!("v: {}", value);
}
所以结论是, 如果你的类型是一次性用品, 你可以直接对其实现 Iterator
手动实现迭代器
如果你向手动实现类似于容器的东西, 那么它当然不是一次性的. 我们应该仿照 Rust 中对切片的迭代器实现.
- 同时实现会转移所有权和不会转移所有权的两个迭代器
- 对
self和&self都实现IntoIterator, 这样就可以做不转移所有权的迭代了
类型本身:
struct IntRange {step: i32,end: i32
}
两个迭代器:
struct IntRangeIter<'a> {range: &'a IntRange,current: i32,
}struct IntRangeIntoIter {range: IntRange,current: i32,
}
两个迭代器实现:
impl Iterator for IntRangeIter<'_> {type Item = i32;fn next(&mut self) -> Option<Self::Item> {if self.current == self.range.end {return None;} else {let current = self.current;self.current += self.range.step;return Some(current);}}
}impl Iterator for IntRangeIntoIter {type Item = i32;fn next(&mut self) -> Option<Self::Item> {if self.current == self.range.end {return None;} else {let current = self.current;self.current += self.range.step;return Some(current);}}
}
实现返回两种迭代器的 IntoIterator:
impl<'a> IntoIterator for &'a IntRange {type Item = i32;type IntoIter = IntRangeIter<'a>;fn into_iter(self) -> Self::IntoIter {IntRangeIter {range: self,current: 0}}
}impl IntoIterator for IntRange {type Item = i32;type IntoIter = IntRangeIntoIter;fn into_iter(self) -> Self::IntoIter {IntRangeIntoIter {range: self,current: 0}}
}
使用它:
let range = IntRange { step: 1, end: 10 };// 可以使用引用来进行 for 循环
for value in &range {println!("v: {}", value);
}// 也可以直接对其进行 for 循环
for value in range {println!("v: {}", value);
}
切片对迭代的实现
我们知道, Rust 的切片有一个 iter 方法, 其实它就相当于对当前切片的引用调用 into_iter.
其实, 在调用切片引用的 into_iter 方法时, 本质上就是调用的其 iter 方法. 方法的实现是在 iter 内的.
let v = vec![1, 2, 3];// 下面两个调用是等价的
let iter1 = v.iter();
let iter2 = (&v).into_iter();
如果你希望实现迭代变量可变的迭代器, 还可以为 &mut T 实现 into_iter, 当然, Rust 内部对于切片的实现, 也是这样的:
let mut v = vec![1, 2, 3];// 下面两个调用是等价的
let mutIter = v.iter_mut();
let mutIter = (&mut v).into_iter();
总结
两种类型:
-
对于一次性使用的类型, 可以直接对其实现迭代器 trait.
-
对于容器, 不应该对容器本身直接实现迭代器, 而是应该单独创建迭代器类型, 然后对其本身实现
IntoIterator
为了方便用户使用, 调用之间的实现应该是这样:
- 实现
T的IntoIterator - 实现
&T的iter函数, 返回借用的迭代器. - 实训
&mut T的iter_mut函数, 返回可变借用的迭代器. - 对
&T和&mut T实现into_iter函数, 并在内部调用刚刚实现的iter和iter_mut函数.
这样, 用户就可以直接调用 iter 方法获得借用的迭代器, 然后使用 map, filter 等方法进行集合的复杂操作了
相关文章:

[Rust] 可迭代类型, 迭代器, 如何正确的创建自定义可迭代类型
在 Rust 中, for 语句的执行依赖于类型对于 IntoIterator 的实现, 如果某类型实现了这个 trait, 那么它就可以直接使用 for 进行循环. 直接实现 在 Rust 中, 如果一个类型实现了 Iterator, 那么它会被同时实现 IntoIterator, 具体逻辑是返回自身, 因为自身就是迭代器. 但是如…...

MySQL中,text,mediumtext, 和 longtext字符类型
需求 由于项目需要,需要在mysql数据库,储存长文本,长文本格式可能为markdown也可能为html。 思路 测试存入html时,字符类型为varcar 255。很明显字符长度达不到要求。数据库抛错,修改字符类型 解决方案 将原本的字…...
网页开发 JS基础
目录 JS概述 基本语法 数据类型内置方法 DOM对象 查找标签 绑定事件 操作标签 jQuery 查找标签 绑定事件 操作标签 Ajax请求 数据接口 前后端分离 ajax的使用 JS概述 一门弱类型的编程语言,属于基于对象和基于原型的脚本语言. 1 直接编写<script>console…...
如何在财税行业查找批量客户?
现在市场上代记账公司也不算少,做过这行的都知道,最初呢行业竞争不强,都是靠地推、老客户转介绍,或者长期以往的蹲守各个地区的工商注册服务中心,找那些才注册企业的老板或者创业者。但是,随着市场经济的发…...

IntelliJ IDEA详细完整安装教程
IntelliJ IDEA 是一款强大的Java集成开发环境,以下是安装和使用教程: 1. 下载IntelliJ IDEA:访问JetBrains官网(jetbrains.com),点击“Download”按钮,选择适合自己操作系统的版本进行下载。 2.…...
)
【.NET Core】Linq查询运算符(一)
【.NET Core】Linq查询运算符(一) 文章目录 【.NET Core】Linq查询运算符(一)一、概述二、筛选数据三、投影运算3.1 Select 3.2 SelectMany3.3 Zip3.4 Select 与 SelectMany 四、Set(设置)运算4.1 Distinct…...

Python sorted函数及用法以及如何用json模块存储数据
Python sorted函数及用法 sorted() 函数与 reversed() 函数类似,该函数接收一个可迭代对象作为参数,返回一个对元素排序的列表。 在交互式解释器中测试该函数,可以看到如下运行过程: >>> a [20, 30, -1.2, 3.5, 90, 3.…...
使用opencv将sRGB格式的图片转换为BT.2020格式【sRGB】【BT.2020】
将sRGB格式的图片转换为BT.2020格式涉及到两个步骤:首先将sRGB转换到线性RGB,然后将线性RGB转换到BT.2020。这是因为sRGB图像通常使用伽马校正,而BT.2020工作在线性色彩空间中。 从sRGB到线性RGB:sRGB图像首先需要进行伽马校正解码…...

聊天注意事项
聊天成功的核心就是双方都能舒服 有些人不会聊天是缺乏引导性 聊天聊两句话就没了 聊天要把话题引导向对方 从倾诉者变为倾听者 才能不断交流 沟通不是一个人的独角戏 每个人都渴望被理解 要注意倾听别人说的话 不要只顾自己说一大堆,别人都瞌睡了 不要查户口式问…...
12.5 作业
1, 以下是一个简单的比喻,将多态概念与生活中的实际情况相联系: 比喻:动物园的讲解员和动物表演 想象一下你去了一家动物园,看到了许多不同种类的动物,如狮子、大象、猴子等。现在,动物园里有…...

深入理解指针3
hello,各位小伙伴,本篇文章跟大家一起继续深入学习指针,感谢大家对我上一篇的支持,如有什么问题,还请多多指教 如果本篇文章对你有帮助,还请各位点点赞!!! 话不多说&am…...

大数据环境下在线考试系统安全策略研究
摘 要 随着云计算、物联网、电子商务、企业信息化等的飞速发展,以及智能终端和各种检测、感应设备的普及和建设,全球逐渐进入信息化、网络化,由此产生了指数爆炸般的数据增长,一个大规模生产、分享和应用的数据的时代正在开启&am…...
Python中程序的异常处理
Python程序一般对输入有一定要求,担当实际输入不满足程序要求时,可能会产生程序的运行错误。Python语言使用的保留太容易try和except进行异常处理! try: 语句块1 except: 语句块2 语句块1是正常执行的程序内容,当这个语句块发生异…...
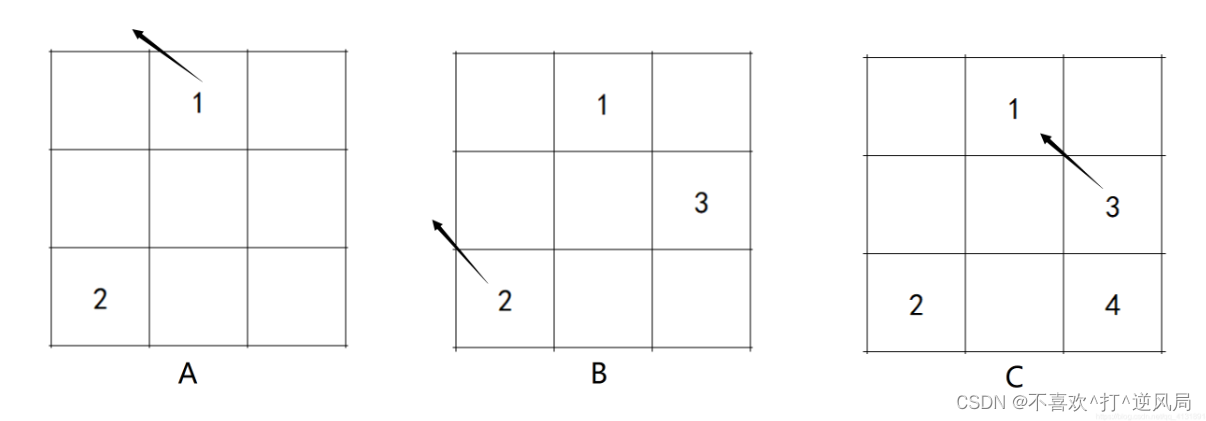
有趣的代码——有故事背景的程序设计3
这篇文章再和大家分享一些有“背景”的程序设计,希望能够让大家学到知识的同时,对编程学习更感兴趣,更能在这条路上坚定地走下去。 目录 1.幻方问题 2.用函数打印九九乘法表 3.鸡兔同笼问题 4.字数统计 5.简单选择排序 1.幻方问题 幻方又…...

聚观早报 |国行PS5轻薄版开售;岚图汽车11月交付7006辆
【聚观365】12月2日消息 国行PS5轻薄版开售 岚图汽车11月交付7006辆 比亚迪推出12月限时优惠 特斯拉正式交付首批Cybertruck 昆仑万维发布「天工 SkyAgents」平台 国行PS5轻薄版开售 索尼最新的PlayStation5主机(CFI-2000型号组-轻薄版)国行版本正…...
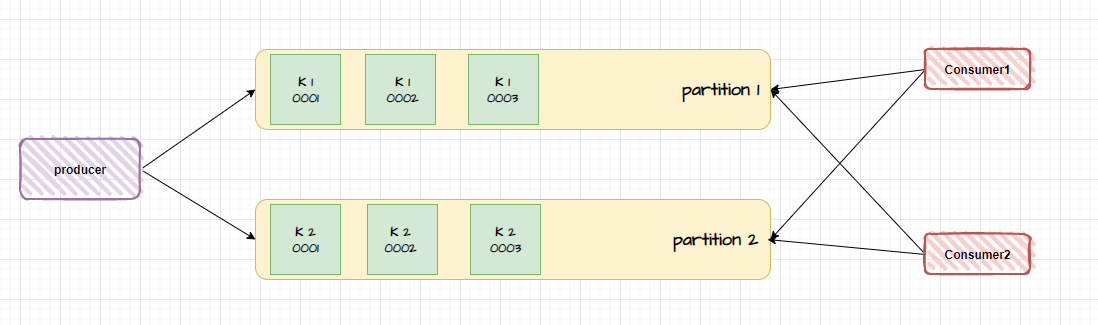
Kafka 保证消息消费全局顺序性
当有消息被生产出来的时候,如果没有指定分区或者指定 key ,那么消费会按照【轮询】的方式均匀地分配到所有可用分区中,但不一定按照分区顺序来分配 我们知道,在 Kafka 中消费者可以订阅一个或多个主题,并被分配一个或多…...

3分钟在CentOS 7上离线安装Docker
在CentOS 7上离线安装Docker的详细步骤如下: 环境检查和准备 检查内核版本:Docker要求系统为64位且内核版本至少为3.10。使用命令uname -r查看内核版本。 检查CentOS版本:通过命令cat /etc/redhat-release查看版本信息。 更新yum包࿰…...
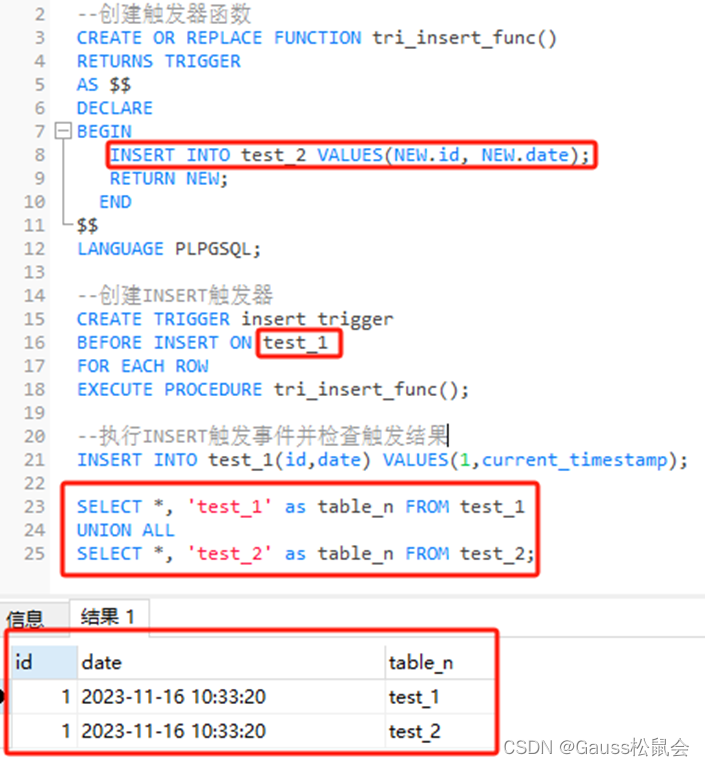
GaussDB数据库SQL系列-触发器
目录 一、前言 二、触发器概念 三、GaussDB数据库中的触发器 1、语法格式 2、创建步骤 3、注意事项 4、附:表和视图上支持的触发器种类 四、GaussDB数据库中的示例 示例一、在GaussDB数据库中创建一个触发器,以便在插入新记录时自动将记录的创建…...
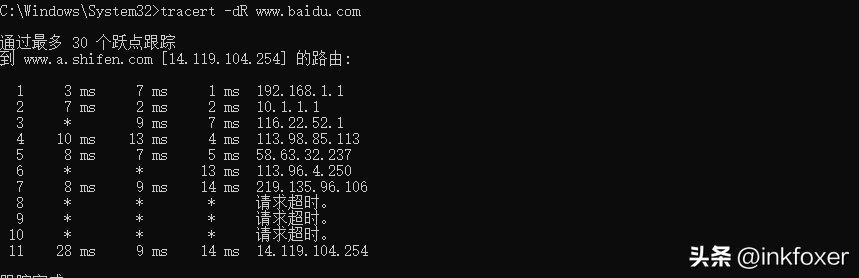
网工学习10-IP地址
一、IP地址概念 IP地址是一个32位的二进制数,它由网络ID和主机ID两部份组成,用来在网络中唯一的标识的一台计算机。网络ID用来标识计算机所处的网段;主机ID用来标识计算机在网段中的位置。IP地址通常用4组3位十进制数表示,中间用…...
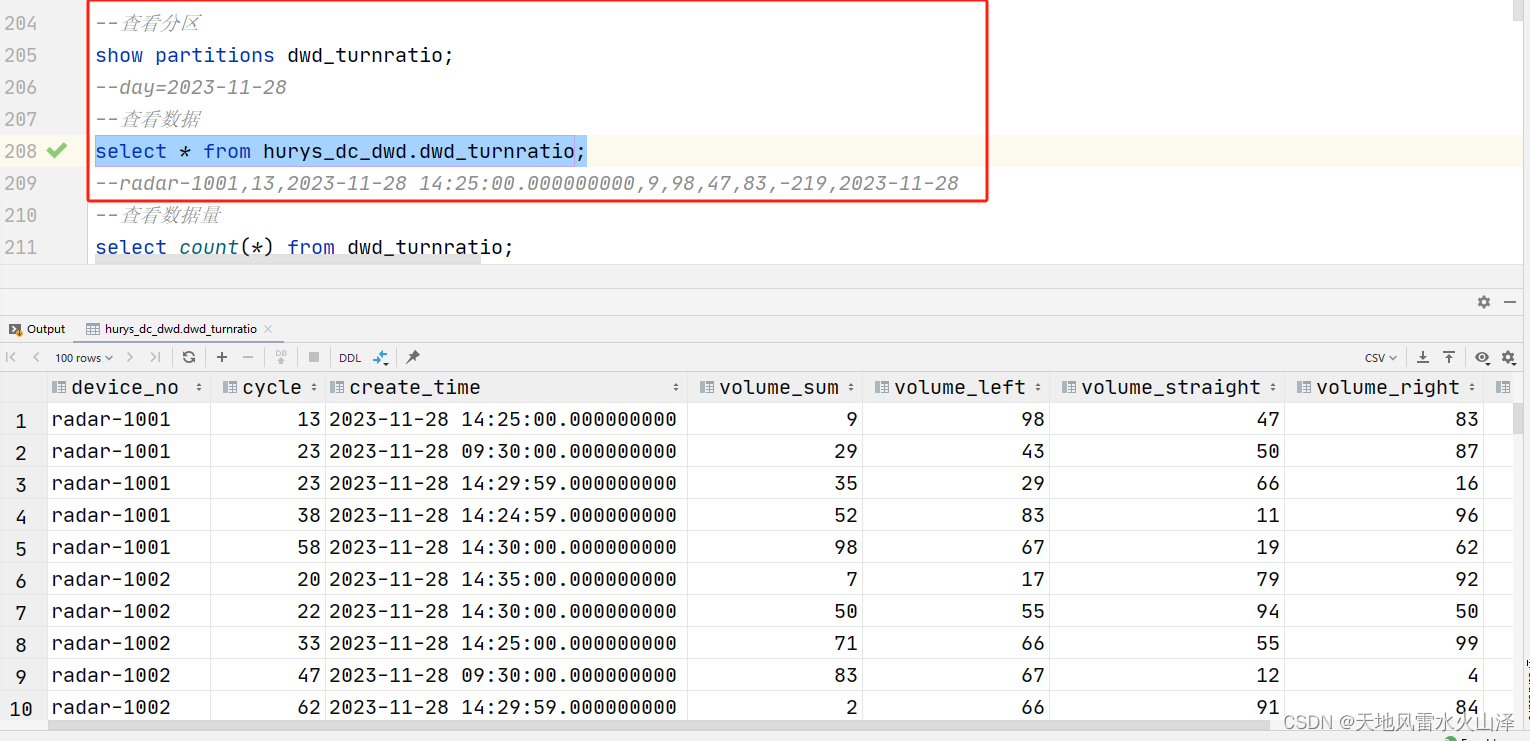
二百零八、Hive——HiveSQL异常:Select查询数据正常,但SQL语句加上group by查询数据为空
一、目的 在HiveSQL的DWD层中,需要对原始数据进行去重在内的清洗,结果一开始其他数据类型的清洗工作都正常,直到碰到转向比数据。 一般的SQL查询有数据,但是加上group by以后就没数据; 一般的SQL查询有数据…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

人工智能--安全大模型训练计划:基于Fine-tuning + LLM Agent
安全大模型训练计划:基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标:为安全大模型创建高质量、去偏、符合伦理的训练数据集,涵盖安全相关任务(如有害内容检测、隐私保护、道德推理等)。 1.1 数据收集 描…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...

【安全篇】金刚不坏之身:整合 Spring Security + JWT 实现无状态认证与授权
摘要 本文是《Spring Boot 实战派》系列的第四篇。我们将直面所有 Web 应用都无法回避的核心问题:安全。文章将详细阐述认证(Authentication) 与授权(Authorization的核心概念,对比传统 Session-Cookie 与现代 JWT(JS…...

DAY 26 函数专题1
函数定义与参数知识点回顾:1. 函数的定义2. 变量作用域:局部变量和全局变量3. 函数的参数类型:位置参数、默认参数、不定参数4. 传递参数的手段:关键词参数5 题目1:计算圆的面积 任务: 编写一…...

AxureRP-Pro-Beta-Setup_114413.exe (6.0.0.2887)
Name:3ddown Serial:FiCGEezgdGoYILo8U/2MFyCWj0jZoJc/sziRRj2/ENvtEq7w1RH97k5MWctqVHA 注册用户名:Axure 序列号:8t3Yk/zu4cX601/seX6wBZgYRVj/lkC2PICCdO4sFKCCLx8mcCnccoylVb40lP...
