利大于弊:物联网技术对电子商务渠道的影响
For Better or For Worse: Impacts of IoT Technology in e-Commerce Channel
物联网技术使用传感器和其他联网设备来手机和共享数据,并且被视为一种可以为供应链成员带来巨大的机会的突破性技术。本文的研究背景是:一个提供物联网基础设备的电子商务平台,一个在该平台上销售产品的制造商。本文的研究问题:制造商的IOT投资决策、平台的定价决策,平台的转移支付策略。本文的研究结论:相较于代理模型,在批发价模型中,制造商更愿意投资物联网技术,并且投资更多;仅仅有投资物联网技术的选择就能让制造商和渠道的表现更差,因此物联网技术可能不会对制造商或者整个工业界有好处。
模型部分:
制造商
制造商生产一种智能设备,其现在的基本质量为q,为了着重研究物联网技术的影响,假设q是固定的。
另外,制造商可以依靠平台的物联网基础设施来投资物联网技术来收集用户的使用信息,这些信息可以用于调整产品的设置,以更符合消费者需求,并使消费者直接获利。
物联网带来的额外的功能是a。
物联网技术的成本包括两部分:固定成本(研发成本)和可变成本。
例如一个智能冰箱,当制造商投资物联网技术时,他需要设计对应的芯片和软件。
因此研发成本定义为 k a 2 ka^2 ka2。
在芯片和软件研发出来之后,还需要把它们嵌入设备中,功能越高,那么嵌入成本越高,用 η a \eta a ηa表示。
c是基本质量q的产品所需的生产成本。
假设制造商只销售一类产品,智能产品或者基础产品,而不是同时生产智能产品和基础产品,文章可能证明了现实中制造商倾向于只生产一类产品(在附录中证明了)。
客户
所有的客户在使用智能设备时,依旧可以享受到基础设备的价值。
例如,智能冰箱也可以像普通冰箱一样,仅仅用于存储食物。
然而,智能冰箱有额外的性能,例如,可以提醒主人在库存少的时候购买食品,或者为主人推荐适合的食品。
消费者异质性
假设消费者对智能设备的基础质量q的估值v,均匀分布于0-1.
假设消费者在对共享数据的敏感性上分为两类,一类是高度敏感(比例为 α \alpha α),因此不能享受物联网带来的附加效用a。第二类是不敏感的消费者(privacy-indifferent customers)(比例为 1 − α 1-\alpha 1−α),可以享受到a。
假设在消费者使用一个智能设备之前,它们的敏感类型是私有信息,因此两类消费者为设备支付同样的价格。
不隐私敏感的消费者的效用是:
U i = θ ∗ q + β ∗ a − p U_i = \theta *q +\beta * a - p Ui=θ∗q+β∗a−p
其中, β \beta β是物联网带来的附加价值a的边际效用。
隐私敏感的消费者的效用是:
U s = θ ∗ q − p U_s = \theta *q - p Us=θ∗q−p
令 U i > 0 U_i>0 Ui>0可以得到 θ > ( p − β ∗ a ) / q \theta > (p-\beta * a)/q θ>(p−β∗a)/q
不隐私敏感的消费者的需求是:
D i = ( 1 − ( p − β ∗ a ) / q ) ∗ α D_i = (1-(p-\beta * a)/q)* \alpha Di=(1−(p−β∗a)/q)∗α
类似,隐私敏感客户的需求是:
D s = ( 1 − p / q ) ∗ ( 1 − α ) D_s = (1-p/q)* (1-\alpha) Ds=(1−p/q)∗(1−α)
因此,总需求为:
D t = D i + D s = ( 1 − ( p − β ∗ a ) / q ) ∗ α + ( 1 − p / q ) ∗ ( 1 − α ) = ( q + a ∗ α ∗ β − p ) / q D_t = D_i + D_s = (1-(p-\beta * a)/q)* \alpha + (1-p/q)* (1-\alpha) = (q+ a*\alpha * \beta -p)/q Dt=Di+Ds=(1−(p−β∗a)/q)∗α+(1−p/q)∗(1−α)=(q+a∗α∗β−p)/q
平台:
平台相较于制造商有更多市场权力,因此平台决定定价模型是批发价模型还是代理模型。
平台也会使用一个转移支付机制来最大化自己的利润。例如,每销售一台智能设备,平台会给制造商转移s的利润。这里不严格限制s为正,即,如果s为正,那么转移支付是平台为制造商提供补贴,即鼓励制造商投资物联网技术。如果s是负数,那么转移支付是向制造商收取一个使用物联网技术的许可费。
物联网带来的交叉销售:平台可以通过收集隐私不敏感客户的使用数据产生额外的销售量。
这种对平台的好处是正比于隐私不敏感客户的数量和物联网功能的水平的。建模为: γ ∗ a ∗ D i \gamma * a * D_i γ∗a∗Di。其中, γ \gamma γ是信息的边际价值。
定价模型:
批发价模型:
制造商决定批发价格w,平台决定零售价格p。
制造商的利润是:
π m = ( w − η ∗ a − c + s ) ∗ D t − k ∗ a 2 \pi_m = (w-\eta *a -c+s)*D_t - k* a^2 πm=(w−η∗a−c+s)∗Dt−k∗a2
平台的利润是:
π p = ( p − w − s ) ∗ D t + γ ∗ a ∗ D i \pi_p = (p-w-s)*D_t + \gamma * a * D_i πp=(p−w−s)∗Dt+γ∗a∗Di
渠道总利润是:
π c = π m + π c = ( p − η ∗ a − c ) ∗ D t − k ∗ a 2 + γ ∗ a ∗ D i \pi_c = \pi_m + \pi_c = (p-\eta *a -c)*D_t - k* a^2+ \gamma * a * D_i πc=πm+πc=(p−η∗a−c)∗Dt−k∗a2+γ∗a∗Di
代理模型:
制造商决定零售价格p。
制造商需要支付 λ \lambda λ比例的收益作为佣金给平台。亚马逊是收取一个固定的佣金率,对于电子产品是8%,对于家居产品是15%。因此本文考虑 λ \lambda λ是一个参数(外生),而不是变量。
制造商的利润是:
π m = ( p ∗ ( 1 − λ ) − η ∗ a − c + s ) ∗ D t − k ∗ a 2 \pi_m = (p*(1-\lambda)-\eta *a -c+s)*D_t - k* a^2 πm=(p∗(1−λ)−η∗a−c+s)∗Dt−k∗a2
平台的利润是:
π p = ( p ∗ λ − s ) ∗ D t + γ ∗ a ∗ D i \pi_p = (p*\lambda-s)*D_t + \gamma * a * D_i πp=(p∗λ−s)∗Dt+γ∗a∗Di
渠道总利润不变,依旧是:
π c = π m + π c = ( p − η ∗ a − c ) ∗ D t − k ∗ a 2 + γ ∗ a ∗ D i \pi_c = \pi_m + \pi_c = (p-\eta *a -c)*D_t - k* a^2+ \gamma * a * D_i πc=πm+πc=(p−η∗a−c)∗Dt−k∗a2+γ∗a∗Di
关于参数值的假设:
1.区块链研发成本k是足够大的,因为如果k很小,那么物联网功能a的水平会很高,导致零售价格太高,隐私敏感客户的需求将为0,这不太合理,因为现实中还是有部分购买智能设备的消费者不会选择去共享信息的(证明这些消费者是隐私敏感客户,但仍然会购买)。
2.物联网技术的边际利润足够大,即 α ∗ ( β + γ ) − η > 0 \alpha * (\beta+\gamma)-\eta>0 α∗(β+γ)−η>0。
这里文章解释为 β \beta β是智能设备给消费者带来的福利, γ \gamma γ是平台的交叉销售价值, η \eta η是投资区块链技术的可变成本(嵌入成本)。
3.产品的基础质量足够大,保证制造商在代理模型下仍然会生产产品,即 q ∗ ( 1 − λ ) > c q*(1-\lambda)>c q∗(1−λ)>c。
游戏顺序:
文章考虑一个五阶段模型。
第一阶段,平台(有主导权)选择定价模型(代理模型vs批发价模型)。
第二阶段,制造商决定投资水平a。
第三阶段,平台决定转移支付s(如果转移支付在制造商定价后才确定,那么转移支付对消费者需求就不起作用)。
第四阶段,如果平台选择了批发价模型,那么制造商决定批发价格w,然后平台决定零售价格p。
如果平台选择了代理模型,那么制造商决定零售价格p。
第五阶段,消费者决定是否购买产品。
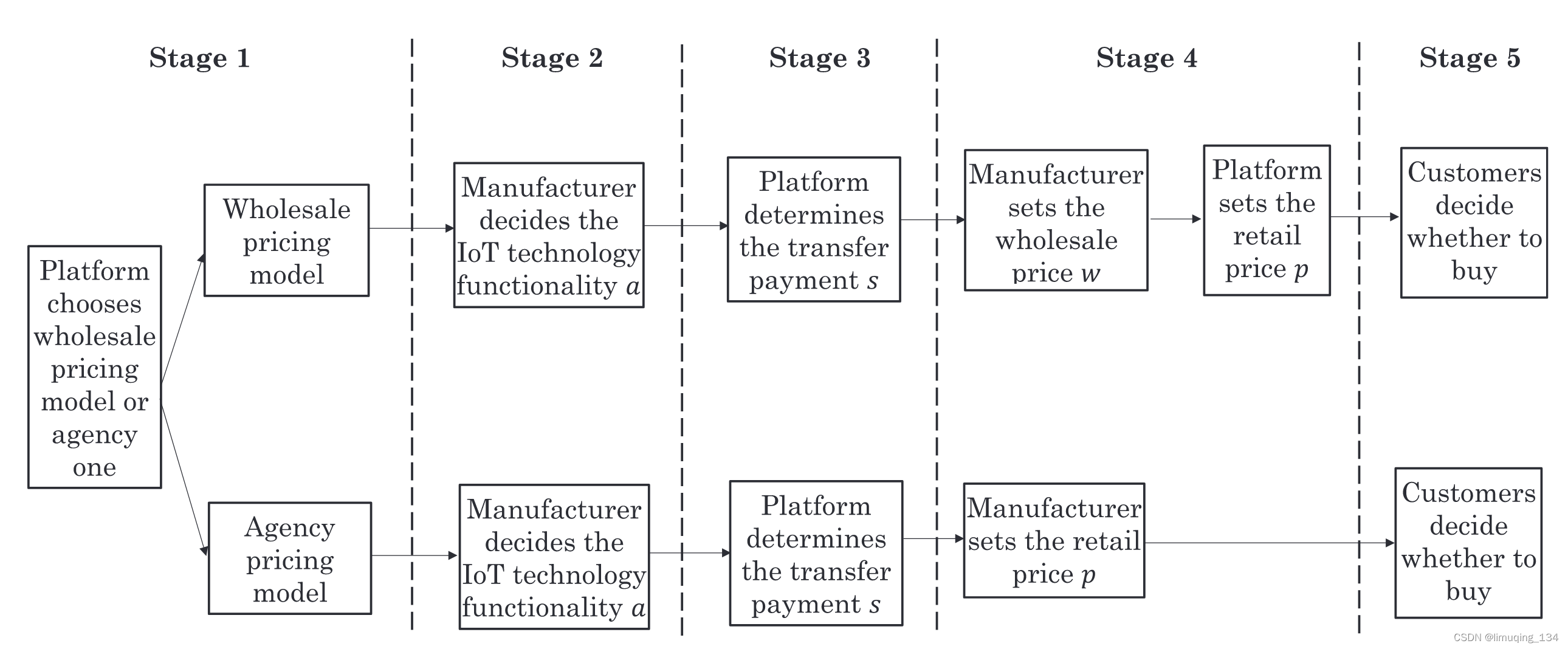
四种情形
(1)WB,即没有物联网技术,批发价模型定价
(2)AB,即没有物联网技术,代理模型定价
(3)WS,即有物联网技术,批发价模型定价
(4)AS,即有物联网技术,代理模型定价
基础模型-没有物联网技术(WB和AB)
此时,物联网功能水平a=0,转移支付s=0
批发价定价模型的子策略均衡
这个子博弈,可以作为有物联网技术的批发价模型的特例(当实施物联网技术的成本k为无限大的时候)进行求解。
代理定价模型的子策略均衡
这个子博弈,不能作为有物联网技术的代理模型的特例进行求解,因为当a趋向于0的时候,转移支付s不能为0。
然后比较在没有物联网技术的情况下,各种参数范围(代理模型下的佣金率 λ \lambda λ、研发成本参数k),两种定价模型下的平台的利润大小,从而确定平台对定价模型的纳什均衡。
得出结论,当佣金率过高或过低的时候,平台会选择批发价模型,当佣金率处于中等的时候,平台会选择代理模型。
解释:
当佣金率较低的时候,如果采取代理模型,平台的利润会很低,因此平台会选择批发价模型。
代理模型下,零售价格会随着佣金率增加而增加,当佣金率非常大的时候,制造商需要设置一个非常高的零售价格,需求量就会减少,于是平台的利润也会比批发价模型下更低,因此平台会选择批发价模型。
因此,平台会在佣金率中等的时候,选择代理模型,因为批发价模型会suffer from双重边际效应,代理模型则无此问题。
有物联网技术(WS和AS)
批发价定价模型的子策略均衡
平台不需要设置转移支付s来最大化其利润。例如,当有转移支付时,批发价格为w0,零售价格为p0,转移支付为s0。
没有转移支付时,制造商只需要将批发价w设置为w0+s0即可,利润还是一样的。
因此,在之后的批发价模型中,均假设s=0。
逆向归纳法求解,求出之后,比较了在不同参数范围( γ \gamma γ)内,零售价格和批发价格的大小、制造商利润和平台利润的大小。
当交叉销售效应 γ \gamma γ比较大的时候,批发价格甚至会高于零售价格,这个结果乍看之下比较奇怪。但可以解释:平台可受益于信息价值带来的交叉销售,因此它有动机减少零售价格(甚至低于批发价格),来扩大需求量,从而得到更多信息。此时,平台的利润甚至会比制造商更高(在没有物联网技术的批发价模型下,制造商的利润总是高于平台)。
然后分析了不同参数范围内( γ \gamma γ(交叉销售效应)、 β \beta β(客户的物联网边际效用))(、k(物联网研发边际成本)),物联网技术的价值对利润的影响
平台的利润和制造商的利润都随着 γ \gamma γ、 β \beta β递增,随着k递减。
然后比较了WB和WS下的均衡结果
在WS下,总需求总是高于WB,批发价格总是高于WB。
当 γ \gamma γ相较于 β \beta β较大时,WS下的零售价格低于WB,否则会高于WB。
制造商和平台的利润在WS下都高于WB。
推论:在批发价模型中,制造商总是会投资物联网技术(a>0)。
代理定价模型的子策略均衡
分析了在代理模型下,各个参数对制造商利润和平台利润的影响:都随着 β \beta β、 γ \gamma γ递增,随着k递减。
这与批发价模型下的结论一致。
然后分析了转移支付s的属性:当佣金率小的时候,平台应该用转移支付s作为许可费(s<0);否则,应该作为补贴(s>0)。
然后分析了代理模型下,制造商的物联网技术投资策略:当佣金率较低,制造商选择不投资物联网技术,即(a=0);否则,制造商选择投资物联网技术(a>0)。
由于制造商对是否投资物联网技术的决策,是以预测的转移支付s为基础的,因此需要综合考虑平台的转移支付决策和制造商的物联网技术投资决策。
当 λ \lambda λ比较小的时候,平台会收取一个许可费,因此制造商不太愿意投资,因此a=0,s=0。
当 λ \lambda λ比较大的时候,平台会提供一个补贴,因此制造商愿意投资,因此a>0,s>0。
还研究了一些关于 γ \gamma γ的一些有趣的结论。当 γ \gamma γ比较小(相较于 β \beta β的时候,平台从交叉销售那里获利有限,因此他会向制造商收取一个许可费。
即使平台会提供一个补贴,在某些范围内,制造商也不会投资物联网技术,原因是制造商需要承担物联网技术成本,但是带来的益处 β \beta β很小。
然后文章分析了代理模型下投资物联网(AS)和不投资物联网(AB)的利润比较
在代理模式下,当制造商投资物联网技术时,平台的利润更高。
与批发价模型不同,会出现,在某些区域,平台希望制造商投资物联网技术,但是制造商不愿意投资的情况。在这些区域,需要一些额外的协调机制来帮助提高总渠道利润。
上述研究都是,在(没有)有物联网的情况下,平台选择批发价或者代理定价模型。
接下来,可以同时分析平台对定价模型的选择和制造商对是否投资物联网技术的选择。
对于AS和WS,WS(批发价)下的投资总是比AS(代理)下大。
AS和WS的投资差异都随着研发成本k增加而减少。
解释:物联网带来的边际利益会因为佣金的存在而减少。
然后分析了哪些参数范围内,会出现AS、AB、WS的子策略完美均衡。
如下图所示:
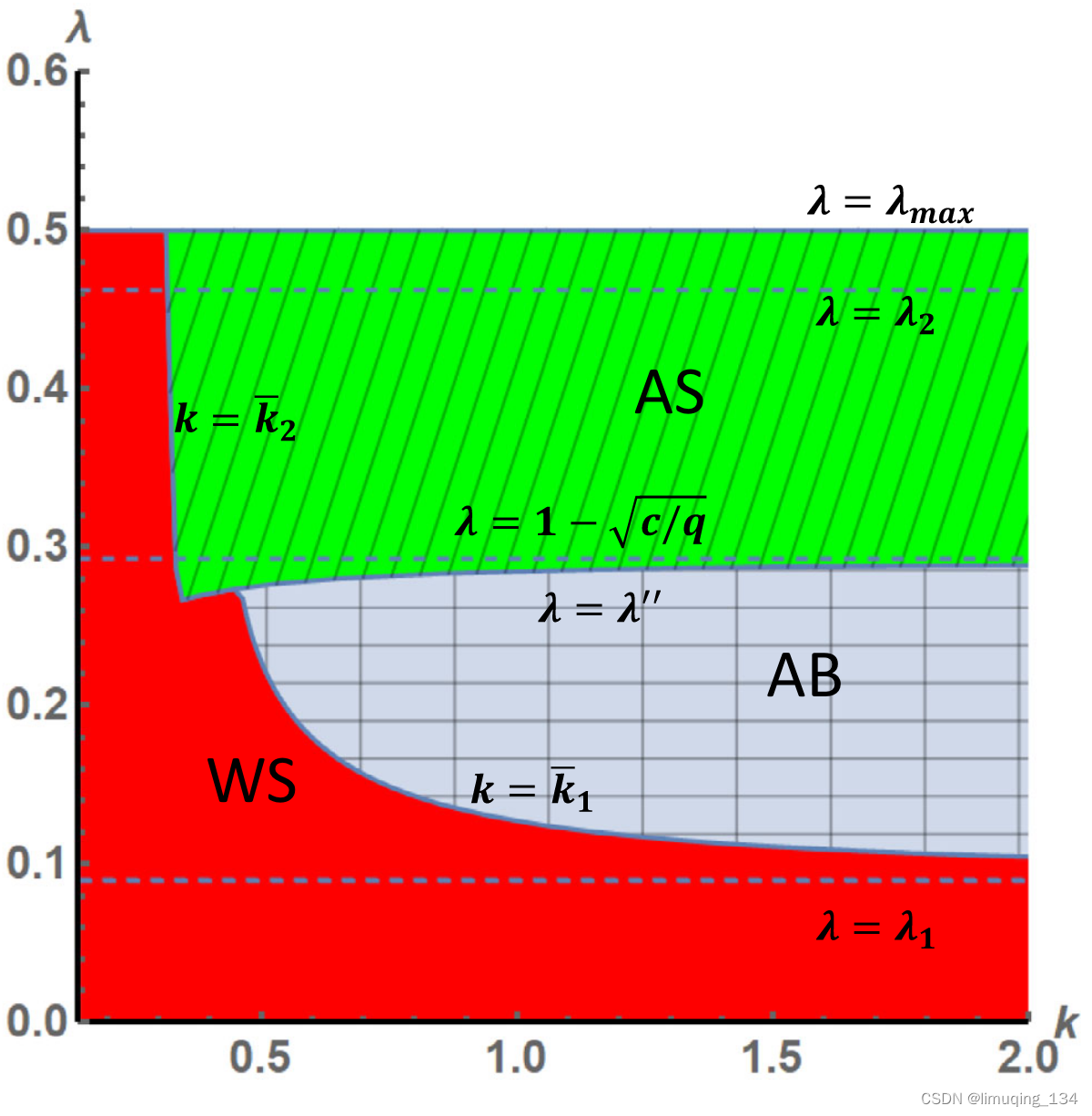
制造商在批发价模型(W)时,总是会选择投资(S)。
当佣金率( λ \lambda λ)较小的时候,平台如果选择代理模型,那么他得到的利润就太少,所以他会选择批发价模型。
然而,当佣金率( λ \lambda λ)较大的时候,平台会选择代理模型(A)。因为代理模型下,平台可以有效使用转移支付来调节制造商的有效边际成本,因此即使制造商面临一个很高的研发成本的时候,制造商也可能选择投资物联网(S),这就导致AS的均衡结果。
随着研发成本k减少,代理模型(更少)和批发价(更多)模型下制造商的投资水平差异变得很大,导致平台选择批发价模型会更有利。
当k足够小的时候,交叉销售带来的好处要超过双重边际效应带来的损失,因此平台会选择批发价模型。
当 λ \lambda λ处于中间范围的时候,如果k较大的时候,物联网的投资不会太大。所以平台选择代理模型来避免双重边际效应,即使制造商不愿意投资物联网技术,这导致了AB的均衡结果。
当k较小的时候,交叉效应的好处比较大,平台于是选择批发价模型,制造商也会投资物联网技术,所以出现WS的均衡结果。
物联网技术的影响
接下来研究了物联网技术改进的影响和物联网技术对供应链的影响,以及其如何通过渠道协调增加社会福利、消费者剩余和渠道利润。
首先研究是否物联网技术改进(k的减少、 β \beta β、 γ \gamma γ的增加)总会对供应链有利。
结论:
(1)当子策略均衡从AB转向AS或者从WS转向AS时,平台的利润增加。
(2)如果因为研发成本减少,子策略均衡从AB(AS)转向WS,制造商利润增加。如果因为研发成本增加,子策略均衡从WS转向AS,或者从AB转向WS,制造商利润减少。
(3)如果因为研发成本减少,子策略均衡从AB转向WS,或者如果因为研发成本增加,从WS转向AS,那么整个渠道的利润增加。如果因为研发成本增加,从AS转向WS,那么整个渠道的利润减少。如果因为研发成本减少,从WS转向AS,那么整个渠道的利润减少。如果因为研发成本增加,从AB转向WS,那么整个渠道的利润减少。
然后分析了物联网技术对利润和福利的影响。
命题5:
当初始均衡是WB的时候,
如果均衡变为AS,制造商利润减少。否则(AW)制造商的利润增加。
平台的利润、整个渠道的利润、消费者剩余、这个那个社会福利增加。
当初始均衡是AB的时候,
如果制造商投资物联网。平台的利润总是增加。
当均衡变为WS的时候,在k比较大的时候,制造商的利润减少,否则制造商的利润增加。
当均衡变为WS的时候,k较大的时候,渠道利润减少,否则,渠道利润增加。
当均衡变为WS的时候,k较大的时候,消费者剩余和社会福利减少。当均衡变为AS,k较大的时候, λ \lambda λ较小的时候,消费者剩余和社会福利减少。
渠道协调和社会福利分析
通过之前的研究,我们知道,社会福利、消费者剩余、渠道利润会在有物联网技术的时候减少。
因此,在接下来的部分,会探索是否渠道协调可以增加社会福利、消费者剩余和渠道利润。
比较了the first-best(FB)和纳什均衡(NB),以及AS和WS。
在FB中,假设有一个社会规划者最大化总体的社会福利。在NB中,平台和制造商通过他们的议价权(bargaining power)共享渠道利润。
让 Λ \Lambda Λ是制造商的议价权,1- Λ \Lambda Λ是平台的议价权,则在NB中,有制造商的利润=渠道利润* Λ \Lambda Λ。平台的利润=渠道利润*(1- Λ \Lambda Λ)。
平台可以使用利益共享机制来实现批发价模型下的NB结果:即平台给制造商共享总利润的 ϕ 1 \phi1 ϕ1比例,以及共享制造商研发成本的 ϕ 2 \phi2 ϕ2比例。所以这个NB讨价还价问题就变成:
max_{w,a,p, ϕ 1 \phi1 ϕ1, ϕ 2 \phi2 ϕ2}( π \pi πc)
其中 π \pi πc是渠道总利润= π \pi πm+ π \pi πp(制造商利润+平台利润)
然后得到纳什讨价还价结果:
w=a* η \eta η+c
ϕ 1 = Λ \phi1=\Lambda ϕ1=Λ
ϕ 2 = 1 − Λ \phi2=1-\Lambda ϕ2=1−Λ
即制造商应该得到与他的议价能力 Λ \Lambda Λ成正比的利润比例,并且平台应该分担与他的议价能力1- Λ \Lambda Λ成正比的研发成本。并且制造商的批发价格应该正好等于其边际成本。
然后,文章比较了FB、NB、AS和WS这几种情况下的社会福利、消费者剩余和渠道利润。
结论:
就社会福利而言,FB>NB,NB>WS,NB>AS。
就渠道利润而言,NB>AS>FB,NB>WS>FB。
就消费者剩余而言,FB>NB,NB>WS,NB>AS。
从上述结果可以看出,FB在增加消费者福利,并且通过增加消费者福利来最大化社会福利而言,是表现最优秀的。
然而,渠道利润却是最少的。
因此,渠道就没动机投资物联网技术,长期依赖就会对创新有不好的影响。
通过纳什讨价还价达成的渠道协调,不仅可以增加渠道利润,也可以增加社会福利和消费者剩余(相比AS和WS)。
因此,应该鼓励平台和制造商采纳纳什讨价还价(NB)策略。
相关文章:

利大于弊:物联网技术对电子商务渠道的影响
For Better or For Worse: Impacts of IoT Technology in e-Commerce Channel 物联网技术使用传感器和其他联网设备来手机和共享数据,并且被视为一种可以为供应链成员带来巨大的机会的突破性技术。本文的研究背景是:一个提供物联网基础设备的电子商务平…...
)
Python 元组详解(tuple)
文章目录 1 概述1.1 性质1.2 下标1.3 切片 2 常用方法2.1 访问:迭代、根据下标2.2 删除:del2.3 运算符:、*2.4 计算元组中元素个数:len()2.5 返回元组中元素最大值:max()2.6 返回元组中元素最小值:min()2.7…...

Redis部署-主从模式
目录 单点问题 主从模式 解析主从模式 配置redis主从模式 info replication命令查看复制相关的状态 断开复制关系 安全性 只读 传输延迟 拓扑结构 数据同步psync replicationid offset psync运行流程 全量复制流程 无硬盘模式 部分复制流程 积压缓冲区 实时复…...

全栈冲刺 之 一天速成MySQL
一、为什么使用数据库 数据储存在哪里? 硬盘、网盘、U盘、光盘、内存(临时存储) 数据持久化 使用文件来进行存储,数据库也是一种文件,像excel ,xml 这些都可以进行数据的存储,但大量数据操作…...

服务器运行train.py报错解决
在服务器配置完虚拟环境以及安装完各种所需库后,发现报错Traceback (most recent call last): File "/root/yolov5-master/yolov5-master/train.py", line 48, in <module> import val as validate # for end-of-epoch mAP File "/root/yolov5…...

Flutter开发type ‘Future<int>‘ is not a subtype of type ‘int‘ in type cast错误
文章目录 问题描述错误源码 问题分析解决方法修改后的代码 问题描述 今天有个同事调试flutter程序时报错,问我怎么解决,程序运行时报如下错误: type ‘Future’ is not a subtype of type ‘int’ in type cast 错误源码 int order Databas…...
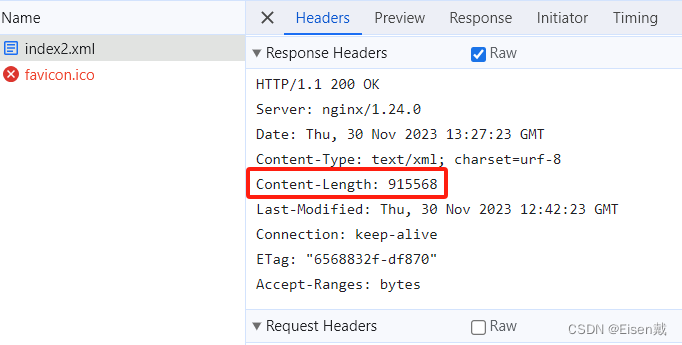
Nginx(十二) gzip gzip_static sendfile directio aio 组合使用测试(2)
测试10:开启gzip、sendfile、aio、directio1m,关闭gzip_static,请求/index.js {"time_iso8601":"2023-11-30T17:20:5508:00","request_uri":"/index.js","status":"200","…...

hls实现播放m3u8视频将视频流进行切片 HLS.js简介
github官网GitHub - video-dev/hls.js: HLS.js is a JavaScript library that plays HLS in browsers with support for MSE.HLS.js is a JavaScript library that plays HLS in browsers with support for MSE. - GitHub - video-dev/hls.js: HLS.js is a JavaScript library …...
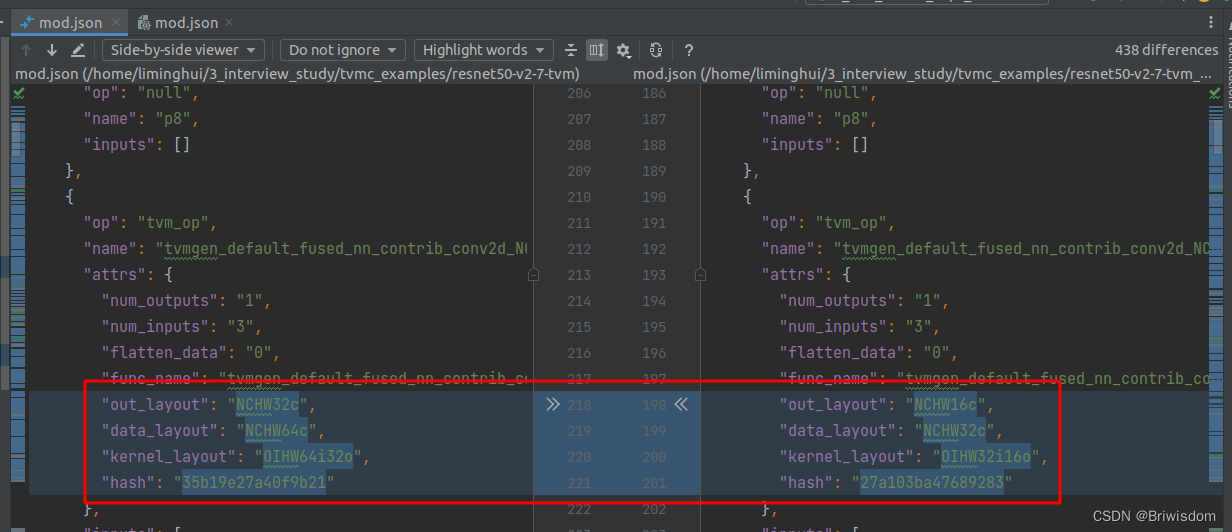
Ubuntu20.04部署TVM流程及编译优化模型示例
前言:记录自己安装TVM的流程,以及一个简单的利用TVM编译模型并执行的示例。 1,官网下载TVM源码 git clone --recursive https://github.com/apache/tvmgit submodule init git submodule update顺便完成准备工作,比如升级cmake版本…...
)
华为OD机试真题-两个字符串间的最短路径问题-2023年OD统一考试(C卷)
题目描述: 给定两个字符串,分别为字符串A与字符串B。例如A字符串为ABCABBA,B字符串为CBABAC可以得到下图m*n的二维数组,定义原点为(0, 0),终点为(m, n),水平与垂直的每一条边距离为1,映射成坐标系如下图。 从原点(0, 0)到(0, A)为水平边,距离为1,从(0, A)到(A, C)为垂…...

python try-except
相比于直接raise ValueError,使用try-except可以使程序在发生异常后仍然能够运行。 在try的部分中,当遇到第一个Error,就跳转到except中寻找对应类型的error,后续代码不再执行,如果try中有多个Error,注意顺…...

flutter开发实战-ValueListenableBuilder实现局部刷新功能
flutter开发实战-ValueListenableBuilder实现局部刷新功能 在创建的新工程中,点击按钮更新counter后,通过setState可以出发本类的build方法进行更新。当我们只需要更新一小部分控件的时候,通过setState就不太合适了,这就需要进行…...
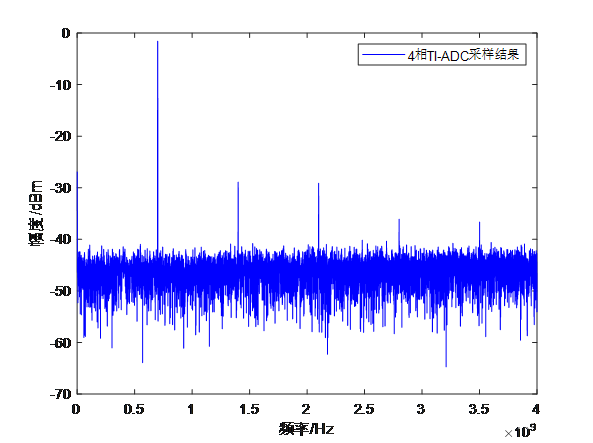
通过时间交织技术扩展ADC采样速率的简要原理
前言 数据采集是将自然界中存在的模拟信号通过模数转换器(ADC)转换成数字信号,再对该数字信号进行相应的接收和处理。数据采集系统作为数据采集的手段,在移动通信、图向采集、无线电等领域有重要作用。随着电子信息技术的飞速发展…...

FluxMQ—2.0.8版本更新内容
FluxMQ—2.0.8版本更新内容 前言 FLuxMQ是一款基于java开发,支持无限设备连接的云原生分布式物联网接入平台。FluxMQ基于Netty开发,底层采用Reactor3反应堆模型,具备低延迟,高吞吐量,千万、亿级别设备连接࿱…...
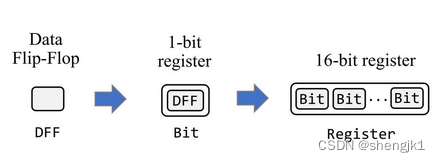
计算机寄存器是如何实现的
冯诺依曼体系 冯诺依曼体系为现代计算机的设计和发展奠定了基础,它的核心思想和原则在当今计算机体系结构中仍然被广泛采用和应用。所以只要谈论计算机的组成就离不开冯诺依曼体系 作为核心组成部分的CPU除了由运算器和控制器组成之外,还有一些寄存器…...

两数之和 三数之和 哈希方法
两数之和 package com; import java.util.*; public class Test5 { //两数之和 public static void main(String[] args) { int[] arr {1,2,3,4,5,6,7,94,42,35}; int target99; Arrays.sort(arr);//快速排序 for(int i0;i<arr.length;i) { int wtarget-arr[i]; int indexA…...

Object Detection in 20 Years: A Survey(2019.5)
文章目录 Abstract1. Introduction1.1. Difference from other related reviews1.2. Difficulties and Challenges in Object Detection 2. OBJECT DETECTION IN 20 YEARS2.1. 目标检测路线图2.1.1. 里程碑:传统探测器(粗略了解)2.1.2. 里程碑:基于CNN的…...

Springboot 设置时区与日期格式
1.配置文件修改(范围修改) spring:jackson:# 东8 北京时区time-zone: GMT8# 日期格式date-format: yyyy-MM-dd HH:mm:ss 2.Java代码修改(范围修改) 2.1 时区 import org.springframework.context.annotation.Bean; import org.…...

从零开始学Go web——第一天
文章目录 从零开始学Go web——第一天一、Go与web应用简介1.1 Go的可扩展性1.2 Go的模块化1.3 Go的可维护1.4 Go的高性能 二、web应用2.1 工作原理2.2 各个组成部分2.2.1 处理器2.2.2 模板引擎 三、HTTP简介四、HTTP请求4.1 请求的文本数据4.2 请求方法4.2.1 请求方法类型4.2.2…...
6.Eclipse里下载Subclipse插件
方法一:从Eclipse Marketplace里面下载 具体操作:打开Eclipse --> Help --> Eclipse Marketplace --> 在Find中输入subclipse搜索 --> 找到subclipse点击install 方法二:从Install New Software里下载 具体操作:打开…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...

Vue3 PC端 UI组件库我更推荐Naive UI
一、Vue3生态现状与UI库选择的重要性 随着Vue3的稳定发布和Composition API的广泛采用,前端开发者面临着UI组件库的重新选择。一个好的UI库不仅能提升开发效率,还能确保项目的长期可维护性。本文将对比三大主流Vue3 UI库(Naive UI、Element …...

数据结构:泰勒展开式:霍纳法则(Horner‘s Rule)
目录 🔍 若用递归计算每一项,会发生什么? Horners Rule(霍纳法则) 第一步:我们从最原始的泰勒公式出发 第二步:从形式上重新观察展开式 🌟 第三步:引出霍纳法则&…...

CppCon 2015 学习:REFLECTION TECHNIQUES IN C++
关于 Reflection(反射) 这个概念,总结一下: Reflection(反射)是什么? 反射是对类型的自我检查能力(Introspection) 可以查看类的成员变量、成员函数等信息。反射允许枚…...
