【矩阵论】Chapter 7—Hermite矩阵与正定矩阵知识点总结复习
文章目录
- 1 Hermite矩阵
- 2 Hermite二次型
- 3 Hermite正定(非负定矩阵)
- 4 矩阵不等式
1 Hermite矩阵
-
定义
设 A A A为 n n n阶方阵,如果称 A A A为Hermite矩阵,则需满足 A H = A A^H=A AH=A,其中 A H A^H AH表示 A A A的共轭转置,也称Hermite转置,具体操作如下:
- 将矩阵的每个元素取共轭。对于复数 a + b i a+bi a+bi,它的共轭是 a − b i a-bi a−bi,其中 a a a和 b b b 是实部和虚部
- 将矩阵的行和列互换
Hermite矩阵与实对称矩阵的性质和证明方法都十分相似
-
Hermite矩阵性质
若 A , B A,B A,B为 n n n阶Hermite矩阵,则
- A A A的所有特征值全是实数
- A A A的不同特征值所对应的特征向量是相互正交的
- 对正整数 k k k, A k A^k Ak也是Hermite矩阵
- 若 A A A可逆,则 A − 1 A^{-1} A−1也是Hermite矩阵
- 对实数 k , p , k A + p B k,p,kA+pB k,p,kA+pB也是Hermite矩阵
-
Hermite矩阵充分必要条件
设 A ∈ C n × n , B ∈ C n × n A\in C^{n\times n},B\in C^{n\times n} A∈Cn×n,B∈Cn×n
-
A A A是Hermite矩阵的充要条件是存在酉矩阵 U U U使得
U H A U = Λ = d i a g ( λ 1 , . . . , λ n ) U^HAU=\Lambda =diag(\lambda_1,...,\lambda_n) UHAU=Λ=diag(λ1,...,λn)
其中 λ 1 , . . . , λ n \lambda_1,...,\lambda_n λ1,...,λn均为实数。实对称矩阵则是存在正交矩阵 U . . . U... U... -
A是Hermite矩阵的充要条件是对任意方阵 S S S, S H A S S^HAS SHAS是Hermite矩阵
-
如果 A , B A,B A,B是Hermite阵,则 A B AB AB是Hermite矩阵的充要条件是 A B = B A AB=BA AB=BA
-
-
相合标准形
设 A A A为 n n n阶Hermite矩阵,则 A A A相合矩阵
D 0 = ( I s 0 0 0 − I r − s 0 0 0 O n − r ) D_0=\begin{pmatrix} I_s & 0 & 0 \\ 0 & -I_{r-s} & 0 \\ 0 & 0 & O_{n-r} \end{pmatrix} D0= Is000−Ir−s000On−r
其中 r = r a n k ( A ) r=rank(A) r=rank(A), s s s是 A A A的正特征值(重特征值按重数计算)的个数。矩阵 D 0 D_0 D0则称为 n n n阶Hermite矩阵 A A A的相合标准形。 -
Sylvester惯性定律
设 A , B A,B A,B为 n n n阶Hermite矩阵,则 A A A与 B B B相合的充要条件是
I n ( A ) = I n ( B ) In(A)=In(B) In(A)=In(B)
其中 I n ( A ) In(A) In(A)称为 A A A的惯性, I n ( A ) = { π ( A ) , v ( A ) , δ ( A ) } In(A)=\{\pi(A),v(A),\delta(A)\} In(A)={π(A),v(A),δ(A)}。其中 π ( A ) \pi(A) π(A), v ( A ) v(A) v(A), δ ( A ) \delta(A) δ(A)分别表示 A A A的正、负和零特征值的个数(重特征值按重数计算)。则 A A A非奇异的充要条件为 δ ( A ) = 0 \delta(A)=0 δ(A)=0且 π ( A ) + v ( A ) = r a n k ( A ) \pi(A)+v(A)=rank(A) π(A)+v(A)=rank(A)。
2 Hermite二次型
-
Hermite二次型定义
由 n n n个复变量 x 1 , . . . , x n x_1,...,x_n x1,...,xn,系数为负数的二次齐式
f ( x 1 , . . . , x n ) = ∑ i = 1 n ∑ j = 1 n a i j x i ˉ x j ˉ f(x_1,...,x_n)=\sum_{i=1}^{n}\sum_{j=1}^{n}a_{ij}\bar{x_i}\bar{x_j} f(x1,...,xn)=i=1∑nj=1∑naijxiˉxjˉ
其中 a i j = a j i a_{ij}=a_{ji} aij=aji,称为Hermite二次型。Hermite二次型可写为 f ( x ) = x H A x f(x)=x^HAx f(x)=xHAx,我们称 A A A的秩就为Hermite二次型的秩。 -
Hermite二次型的标准形定理
对Hermite二次型 f ( x ) = x H A x f(x)=x^HAx f(x)=xHAx,存在酉线性变换 x = U y x=Uy x=Uy(其中 U U U是酉矩阵)使得Hermite二次型 f ( x ) f(x) f(x)变成标准形(只包含平方项的二次型)
f ( x ) = λ 1 y 1 ˉ y 1 + . . . + λ n y n ˉ y n f(x)=\lambda_1\bar{y_1}y_1+...+\lambda_n\bar{y_n}y_n f(x)=λ1y1ˉy1+...+λnynˉyn
其中 λ 1 , . . . , λ n \lambda_1,...,\lambda_n λ1,...,λn为 A A A的特征值。 -
Hermite二次型化标准形(酉线性变换)
设 f ( x ) = x H A x f(x)=x^HAx f(x)=xHAx,其中 A A A为 n n n阶Hermite矩阵
-
求出二次型矩阵 A A A的特征值 λ 1 , . . . λ n \lambda_1,...\lambda_n λ1,...λn和特征向量 v 1 , . . . , v n v_1,...,v_n v1,...,vn,并将特征向量 v 1 , . . . , v n v_1,...,v_n v1,...,vn规范正交
-
令 U = ( v 1 , . . . , v n ) , x = U y U=(v_1,...,v_n),x=Uy U=(v1,...,vn),x=Uy,则
f ( x ) = ( U y ) H A ( U y ) = y H U H A U y = y H ( U H A U ) y = y H Λ y = λ 1 ∣ y 1 ∣ 2 + . . . + λ n ∣ y n ∣ 2 f(x)=(Uy)^HA(Uy)=y^HU^HAUy=y^H(U^HAU)y\\=y^H\Lambda y=\lambda_1|y_1|^2+...+\lambda_n|y_n|^2 f(x)=(Uy)HA(Uy)=yHUHAUy=yH(UHAU)y=yHΛy=λ1∣y1∣2+...+λn∣yn∣2
-
-
Hermite二次型规范形定理
对二次型 f ( x ) = x H A x f(x)=x^HAx f(x)=xHAx,存在可逆线性变换 x = P y x=Py x=Py使得Hermite二次型 f ( x ) f(x) f(x)化为
f ( x ) = y 1 ˉ y 1 + . . . + y s ˉ y s − y s + 1 ˉ y s + 1 − . . . − y r ˉ y r f(x)=\bar{y_1}y_1+...+\bar{y_s}y_s-\bar{y_{s+1}}y_{s+1}-...-\bar{y_r}y_r f(x)=y1ˉy1+...+ysˉys−ys+1ˉys+1−...−yrˉyr
其中 r = r a n k ( A ) , s = π ( A ) r=rank(A),s=\pi(A) r=rank(A),s=π(A)。上式则为Hermite二次型 f ( x ) f(x) f(x)的规范形,其中 s s s和 ( r − s ) (r-s) (r−s)分别称为Hermite二次型的正惯性指数和负惯性指数。
-
二次型化规范形
设 f ( x ) = x H A x f(x)=x^HAx f(x)=xHAx,其中 A A A为 n n n阶Hermite矩阵
-
将二次型化为标准形,得到标准形 f ( x ) = y H Λ y f(x)=y^H\Lambda y f(x)=yHΛy和酉矩阵 U U U
-
将对角线元素提取出来,即只保留 λ i \lambda_i λi的正负性,则
f ( x ) = y H Λ y = y H ( Λ 1 D 0 Λ 1 ) y = y H ( Λ 1 H D 0 Λ 1 ) y = ( Λ 1 y ) H D 0 ( Λ 1 y ) f(x)=y^H\Lambda y=y^H(\Lambda_1 D_0 \Lambda_1)y=y^H(\Lambda_1^HD_0\Lambda_1)y\\ =(\Lambda_1y)^HD_0(\Lambda_1y) f(x)=yHΛy=yH(Λ1D0Λ1)y=yH(Λ1HD0Λ1)y=(Λ1y)HD0(Λ1y)
其中 Λ 1 \Lambda_1 Λ1为对角矩阵,对角线元素为 ∣ λ i ∣ ( 1 ≤ i ≤ n ) \sqrt {|\lambda_i}|(1\leq i \leq n) ∣λi∣(1≤i≤n)。 -
令 y = Λ 1 − 1 z y=\Lambda_1^{-1} z y=Λ1−1z,则
f ( x ) = ( Λ 1 Λ 1 − 1 z ) H D 0 ( Λ 1 Λ 1 − 1 z ) = z H D 0 z = z 1 ˉ z 1 + . . . + z s ˉ y s − z s + 1 ˉ z s + 1 − . . . − z r ˉ z r f(x)=(\Lambda_1\Lambda_1^{-1}z)^HD_0(\Lambda_1\Lambda_1^{-1}z)=z^HD_0z\\=\bar{z_1}z_1+...+\bar{z_s}y_s-\bar{z_{s+1}}z_{s+1}-...-\bar{z_r}z_r f(x)=(Λ1Λ1−1z)HD0(Λ1Λ1−1z)=zHD0z=z1ˉz1+...+zsˉys−zs+1ˉzs+1−...−zrˉzr -
故 x = U Λ − 1 z x=U\Lambda^{-1}z x=UΛ−1z,可逆矩阵 P = U Λ − 1 P=U\Lambda^{-1} P=UΛ−1
-
-
正定相关概念
设 f ( x ) = x H A x f(x)=x^HAx f(x)=xHAx为Hermite二次型
- 如果 f ( x ) > 0 f(x)>0 f(x)>0(等价 s = r = n s=r=n s=r=n),则称 f ( x ) f(x) f(x)为正定的;
- 如果 f ( x ) ≥ 0 f(x)\geq0 f(x)≥0(等价 s = r < n s=r<n s=r<n),则称 f ( x ) f(x) f(x)为半正定(非负定的)的;
- 如果 f ( x ) < 0 f(x)<0 f(x)<0(等价 s = 0 , r = n s=0,r=n s=0,r=n),则称 f ( x ) f(x) f(x)为负定的;
- 如果 f ( x ) ≤ 0 f(x)\leq0 f(x)≤0(等价 s = 0 , r < n s=0,r<n s=0,r<n),则称 f ( x ) f(x) f(x)为半负定的;
- 如果 f ( x ) f(x) f(x)有时为正有时为负(等价 0 < s < r ≤ n 0<s<r\leq n 0<s<r≤n),则称 f ( x ) f(x) f(x)为不定的;
3 Hermite正定(非负定矩阵)
-
定义
根据Hermite二次型的正定(非负定)可以定义Hermite矩阵的正定(非负定)。
设 A A A为 n n n阶Hermite矩阵, f ( x ) = x H A x f(x)=x^HAx f(x)=xHAx
- 如果 f ( x ) > 0 f(x)>0 f(x)>0,则称 A A A为正定的,记作 A > 0 A>0 A>0;
- 如果 f ( x ) ≥ 0 f(x)\geq0 f(x)≥0,则称 A A A为半正定(非负定的)的,记作 A ≥ 0 A\geq 0 A≥0;
- 如果 f ( x ) < 0 f(x)<0 f(x)<0,则称 A A A为负定的,记作 A < 0 A<0 A<0;
- 如果 f ( x ) ≤ 0 f(x)\leq0 f(x)≤0,则称 A A A为半负定的,记作 A ≤ 0 A\leq 0 A≤0;
- 如果 f ( x ) f(x) f(x)有时为正有时为负,则称 A A A为不定的;
-
判断 n n n阶Hermite矩阵 A A A正定
- 通过正定矩阵的定义
- A A A的 n n n个特征值均为正数
- A A A的顺序主子式 Δ k = A ( 1 … k 1 … k ) > 0 , ( k = 1 , . . . , n ) \Delta_k=A\begin{pmatrix}1&\dots&k\\1&\dots&k\end{pmatrix}>0,(k=1,...,n) Δk=A(11……kk)>0,(k=1,...,n)均为正数
- A A A的所有主子式全大于 0 0 0
- 存在 n n n阶非奇异下三角矩阵 L L L,使得 A = L L H A=LL^H A=LLH(该分解称为Cholesky分解)
- 存在 n n n阶非奇异矩阵,使得 A = B H B A=B^HB A=BHB
- 存在 n n n阶非奇异Hermite矩阵 A = S 2 A=S^2 A=S2
-
判断 n n n阶Hermite矩阵 A A A半正定
- 通过半正定矩阵的定义
- A A A的 n n n个特征值均为非负数
- A A A的所有主子式均非负
-
定理证明
设 A , B A,B A,B均为 n n n阶Hermite矩阵,且 B > 0 B>0 B>0,则存在非奇异矩阵 P P P使得
P H A P = d i a g ( λ 1 , . . . , λ n ) , P H B P = I P^HAP=diag(\lambda_1,...,\lambda_n),P^HBP=I PHAP=diag(λ1,...,λn),PHBP=I
其中 λ 1 , . . . , λ n \lambda_1,...,\lambda_n λ1,...,λn是广义特征值问题的特征值证明:
∵ B > 0 \because B >0 ∵B>0
$\therefore 存在非奇异矩阵 存在非奇异矩阵 存在非奇异矩阵P_1 使得 使得 使得P_1^HBP_1=I$
又 ∵ P 1 H A P 1 \because P_1^HAP_1 ∵P1HAP1仍为
Hermite矩阵∴ \therefore ∴酉矩阵 U U U使得
U H ( P 1 H A P 1 ) U = d i a g ( λ 1 , . . . , λ n ) U^H(P_1^HAP_1)U=diag(\lambda_1,...,\lambda_n) UH(P1HAP1)U=diag(λ1,...,λn)
令 P = P 1 U P=P_1U P=P1U∵ P \because P ∵P非奇异,根据定理 P H B P = I P^HBP=I PHBP=I
∴ P H B P = ( P 1 U ) H B ( P 1 U ) = U H P 1 H B P 1 U = I \therefore P^HBP=(P_1U)^HB(P_1U)\\=U^HP_1^HBP_1U=I ∴PHBP=(P1U)HB(P1U)=UHP1HBP1U=I
又 ∵ P 1 \because P_1 ∵P1非奇异,使得 P 1 H B P 1 = I P_1^HBP_1=I P1HBP1=I
∴ \therefore ∴
P H B P = U H P 1 H B P 1 U = U H ( P 1 H B P 1 ) U = U H I U = U H U = I P^HBP= U^HP_1^HBP_1U=U^H(P_1^HBP_1)U\\=U^HIU=U^HU=I PHBP=UHP1HBP1U=UH(P1HBP1)U=UHIU=UHU=I
∴ \therefore ∴
P H A P = U H P 1 H A P 1 U = d i a g ( λ 1 , . . . , λ n ) P^HAP=U^HP_1^HAP_1U=diag(\lambda_1,...,\lambda_n) PHAP=UHP1HAP1U=diag(λ1,...,λn)
∴ \therefore ∴我们可以对上式右乘 P − 1 P^{-1} P−1和 B − 1 B^{-1} B−1,得到
P H B P = I P H = P − 1 B − 1 P^HBP=I \\ P^H=P^{-1}B^{-1} PHBP=IPH=P−1B−1
∴ \therefore ∴ 得到
P − 1 B − 1 A P = d i a g ( λ 1 , . . . , λ n ) P^{-1}B^{-1}AP=diag(\lambda_1,...,\lambda_n) P−1B−1AP=diag(λ1,...,λn)
即 B − 1 A B^{-1}A B−1A相似于对角矩阵,故 λ 1 , . . . , λ n \lambda_1,...,\lambda_n λ1,...,λn是矩阵 B − 1 A B^{-1}A B−1A的特征值,即 λ 1 , . . . , λ n ) \lambda_1,...,\lambda_n) λ1,...,λn)是广义特征值问题的特征值。广义特征值问题 A x = λ B x Ax=\lambda Bx Ax=λBx,左乘 B − 1 B^{-1} B−1,即为 B − 1 A x = λ x B^{-1}Ax=\lambda x B−1Ax=λx
4 矩阵不等式
-
定义
设 A , B A,B A,B都是 n n n阶Hermite矩阵,如果 A − B ≥ 0 A-B\geq 0 A−B≥0则称 A A A大于或等于 B B B(或称 B B B小于等于 A A A),记作 A ≥ B A\geq B A≥B(或 B ≤ A B\leq A B≤A),即 A − B A-B A−B半正定;如果 A − B > 0 A-B>0 A−B>0,则称 A A A大于 B B B(或称 B B B小于 A A A),记作 A > B A>B A>B(或 B < A B<A B<A),即== A − B A-B A−B正定==。
-
性质
设 A , B , C A,B,C A,B,C均为 n n n阶Hermite矩阵,则
- A ≥ B ( A > B ) ⟺ − A ≤ − B ( − A < − B ) ⟺ A\geq B(A>B) \Longleftrightarrow-A\leq -B(-A<-B)\Longleftrightarrow A≥B(A>B)⟺−A≤−B(−A<−B)⟺对任意 n n n阶可逆矩阵 P P P都有 P H A P ≥ P H B P ( P H A P > P H B P ) P^HAP\geq P^HBP(P^HAP>P^HBP) PHAP≥PHBP(PHAP>PHBP)
- 若 A > 0 ( A ≥ 0 ) , C > 0 ( C ≥ 0 ) A>0(A\geq 0),C>0(C\geq 0) A>0(A≥0),C>0(C≥0),且 A C = C A AC=CA AC=CA,则 A C > 0 ( A C ≥ 0 ) AC>0(AC\geq 0) AC>0(AC≥0)
- 若 A > B A>B A>B, P P P为 n × m n\times m n×m列满秩矩阵,则 P H A P > P H B P P^HAP>P^HBP PHAP>PHBP
- 若 A ≥ B A\geq B A≥B, P P P为 n × m n\times m n×m矩阵,则 P H A P ≥ P H B P P^HAP\geq P^HBP PHAP≥PHBP
-
定理
设 A , B A,B A,B都是 n n n阶Hermite矩阵,且 A ≥ 0 , B > 0 A\geq 0,B>0 A≥0,B>0,则
- B ≥ A B\geq A B≥A的充要条件是 ρ ( A B − 1 ) ≤ 1 \rho(AB^{-1})\leq 1 ρ(AB−1)≤1
- B > A B>A B>A的充要条件是 ρ ( A B − 1 ) < 1 \rho(AB^{-1})<1 ρ(AB−1)<1
设 A A A是 n n n阶Hermite矩阵,则 λ m i n ( A ) I ≤ A ≤ λ m a x I \lambda_{min}(A)I\leq A\leq\lambda_{max}I λmin(A)I≤A≤λmaxI,这时 λ m i n \lambda_{min} λmin和 λ m a x \lambda_{max} λmax分别表示 A A A的最大和最小特征值。
设 A , B A,B A,B均为 n n n阶Hermite正定矩阵,则
- 若 A ≥ B > 0 A\geq B>0 A≥B>0,则 B − 1 ≥ A − 1 > 0 B^{-1}\geq A^{-1}>0 B−1≥A−1>0
- 若 A > B > 0 A>B>0 A>B>0,则 B − 1 > A − 1 > 0 B^{-1}>A^{-1}>0 B−1>A−1>0
设 A , B A,B A,B均为 n n n阶Hermite正定矩阵,且 A B = B A AB=BA AB=BA,则
-
若 A ≥ B A\geq B A≥B,则 A 2 ≥ B 2 A^2\geq B^2 A2≥B2
证明: A 2 − B 2 = ( A − B ) ( A + B ) = ( A + B ) ( A − B ) A^2-B^2=(A-B)(A+B)=(A+B)(A-B) A2−B2=(A−B)(A+B)=(A+B)(A−B),易知 ( A − B ) ≥ 0 , A + B > 0 (A-B)\geq0,A+B>0 (A−B)≥0,A+B>0,则克制
-
若 A ≥ B A\geq B A≥B,则 A 2 > B 2 A^2> B^2 A2>B2
同理得证
设 A A A是 m × n m\times n m×n行满秩矩阵, B B B是 n × k n\times k n×k矩阵,则
B H B ≥ ( A B ) H ( A A H ) − 1 ( A B ) B^HB\geq (AB)^H(AA^H)^{-1}(AB) BHB≥(AB)H(AAH)−1(AB)
等号成立当且仅当存在一个 m × k m\times k m×k矩阵 C C C使得 B = A H C B=A^HC B=AHC
相关文章:

【矩阵论】Chapter 7—Hermite矩阵与正定矩阵知识点总结复习
文章目录 1 Hermite矩阵2 Hermite二次型3 Hermite正定(非负定矩阵)4 矩阵不等式 1 Hermite矩阵 定义 设 A A A为 n n n阶方阵,如果称 A A A为Hermite矩阵,则需满足 A H A A^HA AHA,其中 A H A^H AH表示 A A A的共轭转…...

Golang语言基础之切片
概述 数组的长度是固定的并且数组长度属于类型的一部分,所以数组有很多的局限性 func arraySum(x [3]int) int{sum : 0for _, v : range x{sum sum v}return sum } 这个求和函数只能接受 [3]int 类型,其他的都不支持。 切片 切片(Slic…...

SpringCloud-服务消费者Fegin调用时无法获取异常信息
一、前言 假设有以下需求: 服务消费者A调用服务提供者B往MySQL新增一条人员信息服务提供者做了一个逻辑判断:若无该人员信息则新增,若已存在该人员信息,则返回给消费者异常状态码及异常信息:“请勿添加重复数据” 问…...
re:invent 2023 Amazon Q 初体验
授权声明:本篇文章授权活动官方亚马逊云科技文章转发、改写权,包括不限于在 Developer Centre,知乎,自媒体平台,第三方开发者媒体等亚马逊云科技官方渠道 前言 亚马逊云科技在2023 re:Invent全球大会上宣布推出 Amazon…...
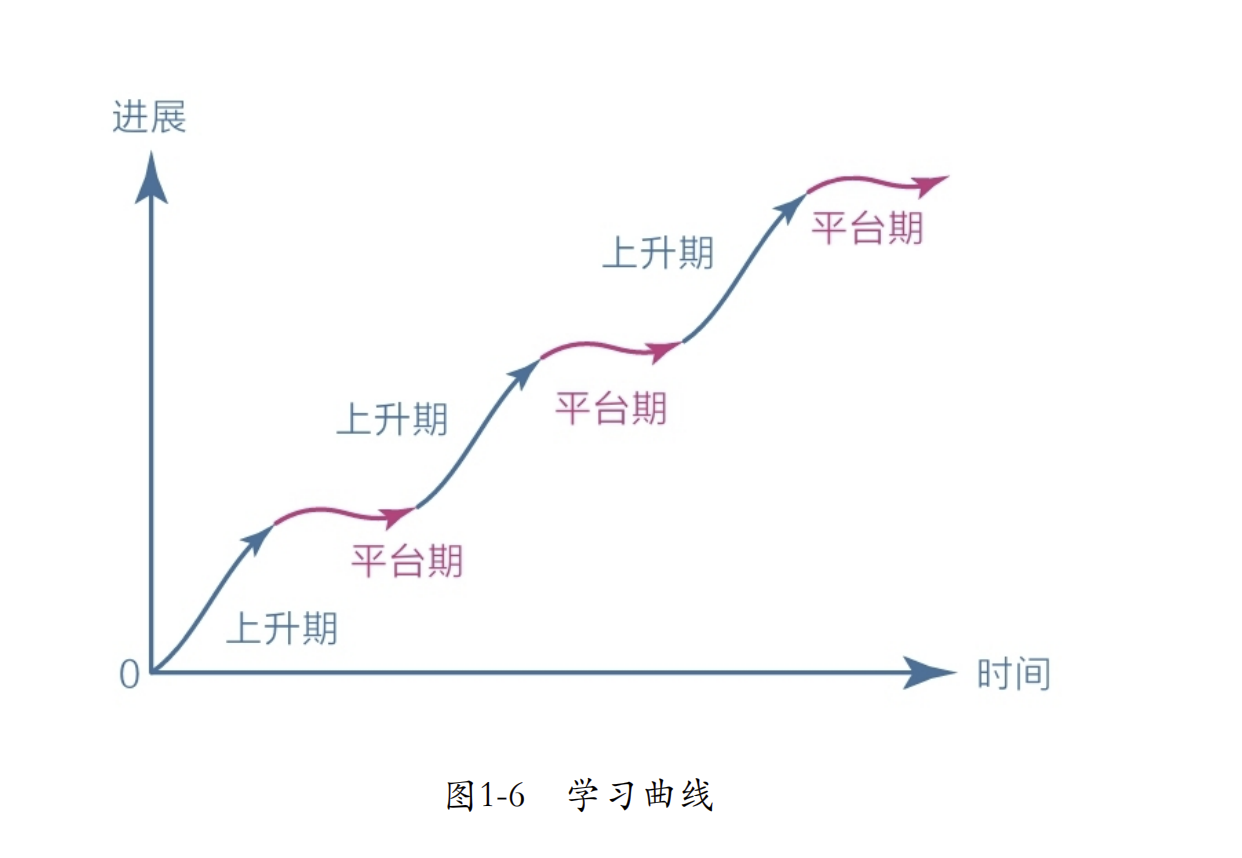
认知觉醒(四)
认知觉醒(四) 第三节 耐心:得耐心者得天下 20世纪八九十年代,金庸的武侠小说风靡全国。如今,虽然几十年过去了,金庸先生也已与世长辞,但他留下的作品依然广受欢迎,被奉为经典。如此成就,自然…...
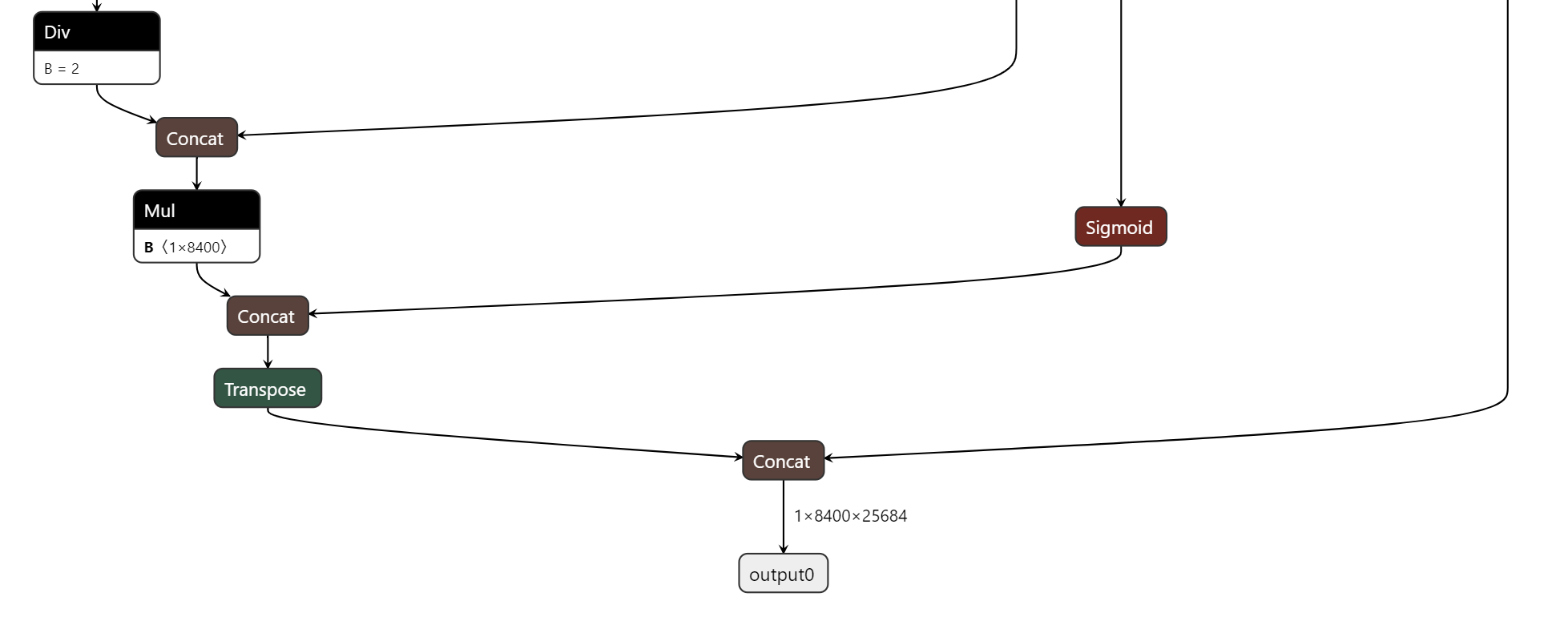
AI模型部署 | onnxruntime部署YOLOv8分割模型详细教程
本文首发于公众号【DeepDriving】,欢迎关注。 0. 引言 我之前写的文章《基于YOLOv8分割模型实现垃圾识别》介绍了如何使用YOLOv8分割模型来实现垃圾识别,主要是介绍如何用自定义的数据集来训练YOLOv8分割模型。那么训练好的模型该如何部署呢?…...

模拟电路学习笔记(一)之芯片篇(持续更新)
模拟电路学习笔记(一)之芯片篇(持续更新) 1.CD4047BE芯片 CD4047是一种包含高电压的多谐振荡器,该器件的操作可以在两种模式下完成,分别是单稳态和非稳态。CD4047需要一个外部电阻器和电容器来决定单稳态…...

如何利用CentOS7+docker+jenkins+gitee部署springboot+vue前后端项目(保姆教程)
博主介绍:Java领域优质创作者,博客之星城市赛道TOP20、专注于前端流行技术框架、Java后端技术领域、项目实战运维以及GIS地理信息领域。 🍅文末获取源码下载地址🍅 👇🏻 精彩专栏推荐订阅👇🏻…...

qt 5.15.2 主窗体事件及绘制功能
qt 5.15.2 主窗体事件及绘制功能 显示主窗体效果图如下所示: main.cpp #include "mainwindow.h"#include <QApplication>int main(int argc, char *argv[]) {QApplication a(argc, argv);MainWindow w;w.setFixedWidth(600);w.setFixedHeight(6…...

(2)(2.4) TerraRanger Tower/Tower EVO(360度)
文章目录 前言 1 安装传感器并连接 2 通过地面站进行配置 3 参数说明 前言 TeraRanger Tower 可用于在 Loiter 和 AltHold 模式下进行目标规避。传感器的最大可用距离约为 4.5m。 TeraRanger Tower EVO 可用于在 Loiter 和 AltHold 模式下进行目标规避。传感器的最大可用…...

Redis_主从复制、哨兵模式、集群模式详解
Redis的主从复制 为什么Redis要引入主从复制?what? 在这里博主为小伙伴们简单的做下解释,可以了解一下 实际生产环境下,单机的redis服务器是无法满足实际的生产需求的。 第一,单机的redis服务器很容易发生单点故障&am…...
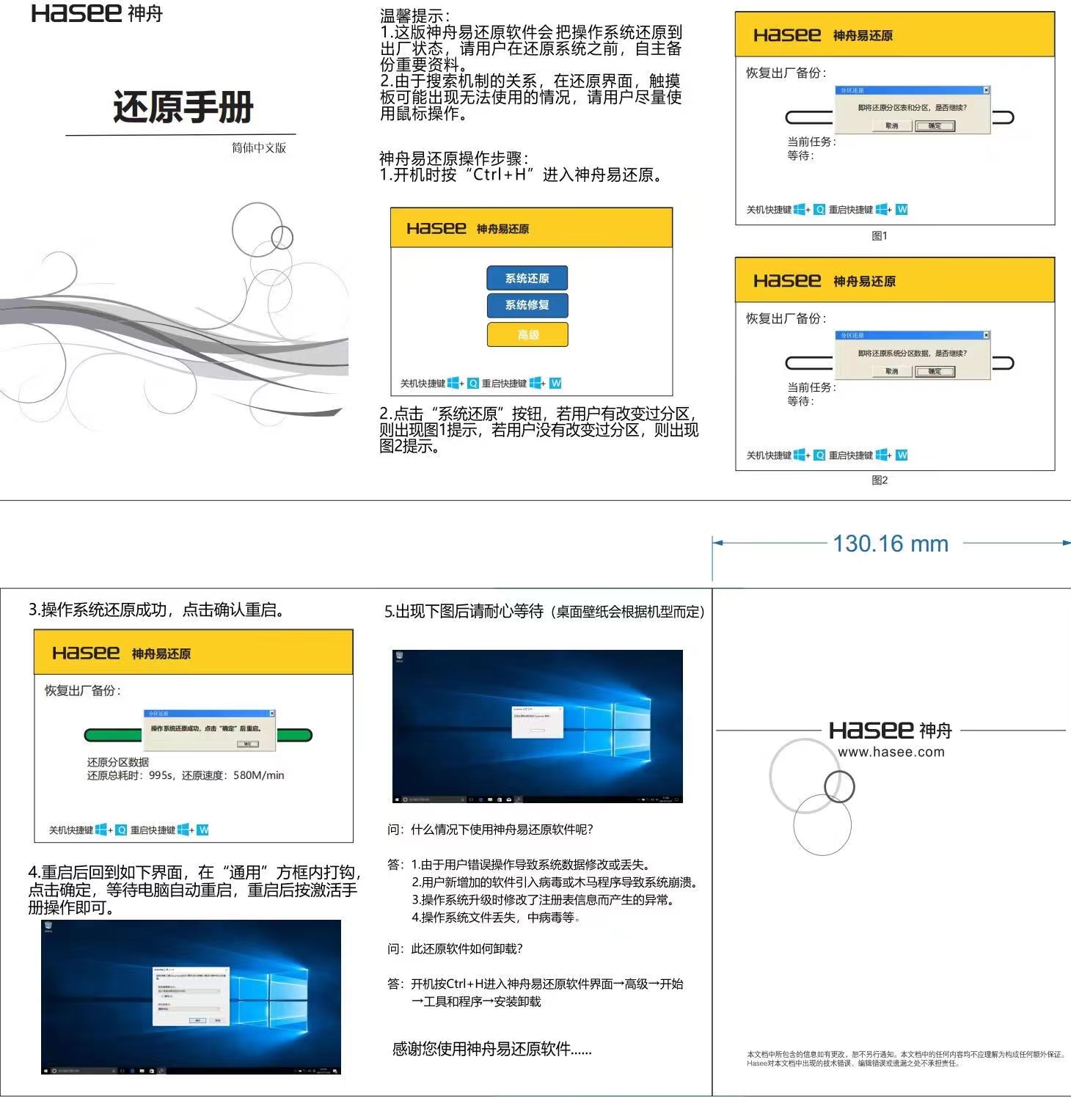
关于神舟-战神TA5NS系统重装问题
加装固态卡在log处无法开机问题 下面是我的步骤 1.按f7选择pe安装系统,然后发现卡在战神log处不转动 2.下载驱动 TA5NS驱动地址 下载RAID驱动(如果没有私信我,我网盘里有),拷到u盘中,然后进入pe系统里面…...
前端大文件上传webuploader(react + umi)
使用WebUploader还可以批量上传文件、支持缩略图等等众多参数选项可设置,以及多个事件方法可调用,你可以随心所欲的定制你要的上传组件。 分片上传 1.什么是分片上传 分片上传,就是将所要上传的文件,按照一定的大小,将…...
数据库常用sql命令)
人大金仓(kingbase)数据库常用sql命令
一. 字段 1. 添加 alter table book add column book_id varchar not null, book_title varchar(10) default ;2. 删除 alter table book drop book_id, book_title;// 外键时 alter table book drop book_id, book_title cascade;3. 修改类型 alter table book alter colu…...

HashMap相关专题
前置知识:异或运算 异或运算介绍 异或有什么神奇之处(应用)? (1)快速比较两个值 (2)我们可以使用异或来使某些特定的位翻转,因为不管是0或者是1与1做异或将得到原值的相…...

threejs WebGLRenderer 像素比对画布大小的影响
官方文档 - WebGLRenderer .setPixelRatio ( value : number ) : undefined 设置设备像素比。通常用于避免HiDPI设备上绘图模糊 .setSize ( width : Integer, height : Integer, updateStyle : Boolean ) : undefined 将输出canvas的大小调整为(width, height)并考虑设备像素比…...
 与 RocketMQTemplate.syncSend() 方法详解)
RocketMQTemplate.send() 与 RocketMQTemplate.syncSend() 方法详解
Apache RocketMQ 是一款强大的分布式消息中间件,与 Spring Boot 集成后,通过 RocketMQTemplate 提供了多种方法来发送消息。其中,send() 和 syncSend() 是两个常用的发送消息方法,本文将深入探讨它们的区别以及详细解释这两个方法…...

波奇学C++:类型转换和IO流
隐式类型转换 int i0; double pi; 强制类型转换 int* pnullptr; int a(int)p; 单参数构造函数支持隐式类型转换 class A { public:A(string a):_a(a){} private:string _a; }; A a("xxxx"); //"xxx" const char* 隐式转换为string 多参数也可以通过{…...

集成开发环境 PyCharm 的安装【侯小啾python基础领航计划 系列(二)】
集成开发环境PyCharm的安装【侯小啾python基础领航计划 系列(二)】 大家好,我是博主侯小啾, 🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔…...
Java核心知识点整理大全27-笔记(已完结)
目录 30. 云计算 30.1.1. SaaS 30.1.2. PaaS 30.1.3. IaaS 30.1.4. Docker 30.1.4.1. 概念 30.1.4.2. Namespaces 30.1.4.3. 进程(CLONE_NEWPID 实现的进程隔离) 30.1.4.4. Libnetwork 与网络隔离 30.1.4.5. 资源隔离与 CGroups 30.1.4.6. 镜像与 UnionFS 30.1.4.7.…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...
