探索三种生成模型:基于DDPMs、NCSNs和SDEs方法的Diffusion
探索三种生成模型:基于DDPMs、NCSNs和SDEs方法的Diffusion
- 去噪扩散概率模型(DDPMs)
- 正向过程
- 反向过程
- 噪声条件得分网络(NCSNs)
- 正向过程
- 初始化
- 训练 NCSNs
- 生成样本
- 反向过程
- 随机微分方程(SDEs)
- 原理背景
- 正向过程
- 反向过程
- 模型训练与采样
- 采样方法
- 方法可行性解释
去噪扩散模型代表了计算机视觉领域的一个新兴主题,取得了在生成建模方面的显著成果。该模型分为正向扩散阶段和反向扩散阶段。在正向扩散阶段,逐步添加高斯噪声逐渐扰动输入数据;在反向扩散阶段,模型通过学习逆转扩散过程逐步恢复原始输入数据。尽管计算负担较大,但由于生成样本的质量和多样性,扩散模型受到广泛赞赏。
在计算机视觉中,扩散模型已应用于多个任务,包括图像生成、图像超分辨率、图像修复、图像编辑、图像翻译等。此外,扩散模型学到的潜在表示在判别任务中也被发现是有用的,例如图像分割、分类和异常检测。
回顾扩散模型的文章,可将扩散模型分为三个主要子类:
- 去噪扩散概率模型(DDPMs)
- 噪声条件得分网络(NCSNs)
- 随机微分方程(SDEs)
DDPMs使用潜在变量估计概率分布,类似于变分自动编码器。 NCSNs基于训练共享神经网络来估计扰动数据分布的分数函数。 SDEs通过建模正向和反向SDEs实现高效的生成策略。
扩散模型在生成建模任务中取得了显著成果,同时也面临一些限制。未来的研究方向包括进一步探索应用领域、改进计算效率以及提高生成模型的可解释性。
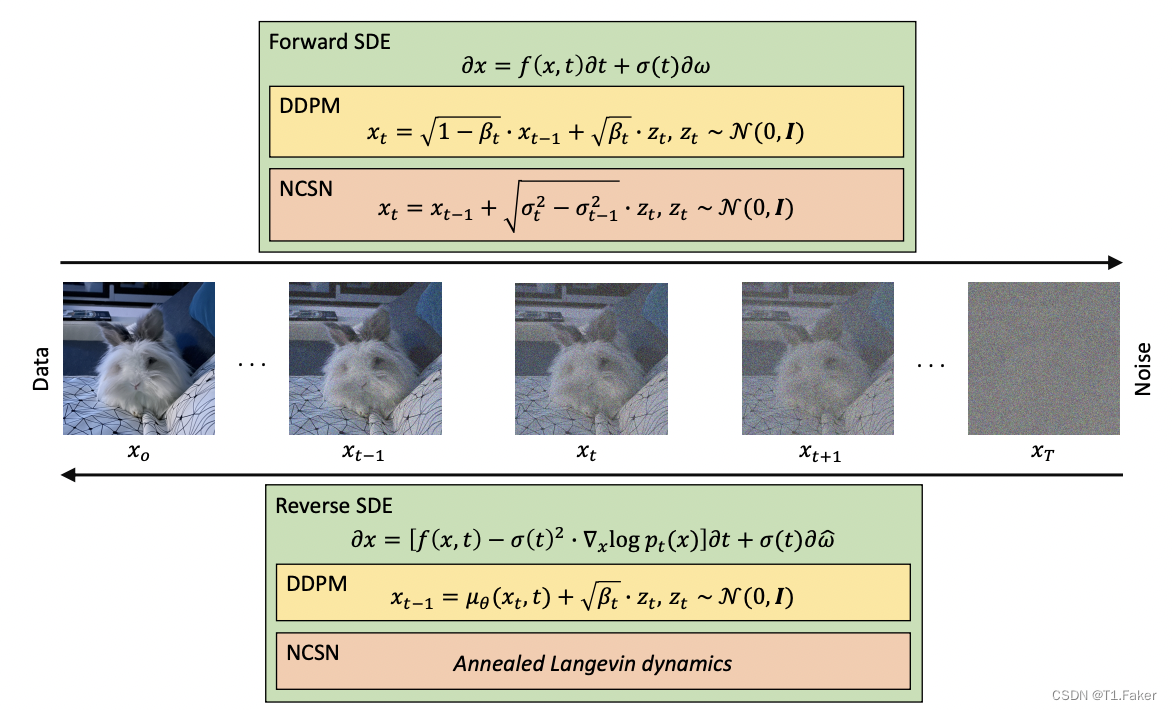
去噪扩散概率模型(DDPMs)
正向过程
在DDPMs中,用 p ( x 0 ) p(x_0) p(x0) 表示原始、未经破坏的训练数据(图像)的概率密度。
概率密度函数描述了在图像空间中每个可能图像的相对概率分布。换句话说, p ( x 0 ) p(x_0) p(x0) 表示了在训练数据集中每个图像出现的概率。
在DDPMs(Denoising Diffusion Probabilistic Models)中, p ( x 0 ) p(x_0) p(x0) 是指模型训练时的初始状态,即未经过任何噪声破坏的原始图像。这个初始状态用于在训练过程中生成具有多样性和质量的图像。模型通过逐步添加高斯噪声来训练,从而逼近或捕捉了训练数据的分布,使其具有一定的鲁棒性和生成能力。
因此, p ( x 0 ) p(x_0) p(x0) 在这里表示模型训练的起点,是学习过程中要模拟的原始图像的概率分布。通过模拟这个概率分布,并在训练中引入逐渐增加的高斯噪声。
给定一个初始状态的训练样本 x 0 ∼ p ( x 0 ) x_0 ∼ p(x_0) x0∼p(x0),通过下面的公式马尔可夫过程获得噪声版本 x 1 、 x 2 . . . , x T x_1、x_2 ...,x_T x1、x2...,xT
p ( x t ∣ x t − 1 ) = N ( x t ; 1 − β t ⋅ x t 1 , β t ⋅ I ) , ∀ t ∈ [ 1 , . . . , T ] p(x_t|x_{t-1}) = N(x_t;\sqrt {1-\beta_t} ·x_{t_1},\beta_t ·I), ∀_t \in [1,...,T] p(xt∣xt−1)=N(xt;1−βt⋅xt1,βt⋅I),∀t∈[1,...,T]
公式解释:
其中 p ( x t ∣ x t − 1 ) p(x_t|x_{t-1}) p(xt∣xt−1) 表示在给定前一步 ( x t − 1 x_{t-1} xt−1) 的条件下,当前步 ( x t x_t xt) 的分布
T T T是扩散步骤的数量, β 1 , . . . , β T ∈ [ 0 , 1 ) β_1, . . . , β_T ∈ [0, 1) β1,...,βT∈[0,1) 是代表扩散步骤中方差变化的超参数, I I I是与输入图像 x 0 x_0 x0具有相同尺寸的单位矩阵,而 N ( x ; µ , σ ) N(x; µ, σ) N(x;µ,σ)表示均值为 µ µ µ和协方差为 σ σ σ的正态分布,产生 x x x。
这个过程可以理解为 x t − 1 x_{t-1} xt−1 分布的基础上,选择一定的均值和方差,在图像 x t − 1 x_{t-1} xt−1 状态下中增加一些正态分布抽样下的噪声。
p ( x t ∣ x t − 1 ) = N ( x t ; 1 − β t ⋅ x t 1 , β t ⋅ I ) , ∀ t ∈ [ 1 , . . . , T ] p(x_t|x_{t-1}) = N(x_t;\sqrt {1-\beta_t} ·x_{t_1},\beta_t ·I), ∀_t \in [1,...,T] p(xt∣xt−1)=N(xt;1−βt⋅xt1,βt⋅I),∀t∈[1,...,T]
上述这个递归公式如果在每一步增加的噪声都是经过均匀的正态分布抽样的话,可以将式子转化为如下:
p ( x t ∣ x 0 ) = N ( x t ; β ^ t ⋅ x 0 , ( 1 − β ^ t ) ⋅ I ) p(x_t|x_0) = N(x_t;\sqrt {\hat \beta_t} ·x_0,(1- \hat \beta_t )·I) p(xt∣x0)=N(xt;β^t⋅x0,(1−β^t)⋅I)
公式解释:
其中 β ^ t = ∏ i = 1 t α i \hat \beta_t=∏_{i=1}^tα_i β^t=∏i=1tαi且 α t = 1 − β t α_t=1−β_t αt=1−βt,基本上式子表示了:如果有原始图像 x 0 x_0 x0并固定方差调度 β t β_t βt,则可以通过单一步骤对任何噪声版本 x t x_t xt进行采样。
前面我们已经知道了如何求在给定前一步 ( x t − 1 x_{t-1} xt−1) 的条件下,当前步 ( x t x_t xt) 的分布,现在要求出本身的图像 x t x_t xt的分布。
这里会用到一个技巧叫重新参数化技巧,通过这个技巧,我们可以从一个标准正态分布 N ( 0 , I ) N(0, I) N(0,I) 中采样样本,并通过线性变换和平移操作,得到原始正态分布 N ( µ , σ 2 ⋅ I ) N(µ, σ² \cdot I) N(µ,σ2⋅I) 中的样本。
这里的标准正态分布 N ( 0 , I ) N(0, I) N(0,I) 对应的是 z t z_t zt,即噪声的分布。原始正态分布 N ( µ , σ 2 ⋅ I ) N(µ, σ² \cdot I) N(µ,σ2⋅I) 对应的是生成的图像 x t x_t xt。
先回顾一下标准正态分布的样本 z ∼ N ( 0 , I ) z \sim N(0, I) z∼N(0,I) 的采样过程:我们从均值为 0,方差为 1 的正态分布中生成一个随机数 z z z。然后,通过乘以标准差 σ σ σ 并加上均值 µ µ µ,我们可以得到原始正态分布 N ( µ , σ 2 ⋅ I ) N(µ, σ² \cdot I) N(µ,σ2⋅I) 中的样本 x x x。这个操作就是重新参数化技巧的基本思想。即:
x = z σ + u x = zσ+u x=zσ+u
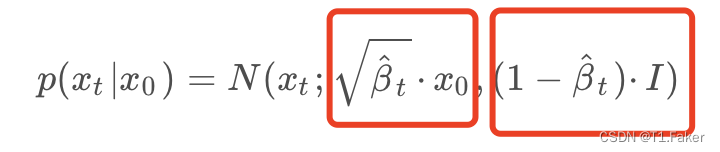
其中 u u u就是左边红框的部分, σ σ σ就是右边红框的部分。将它们带入到下面:
x = z σ + u x = zσ+u x=zσ+u
得:
x t = β ^ t ⋅ x 0 + ( 1 − β ^ t ) ⋅ z t x_t = \sqrt{\hat \beta_t}·x_0 +\sqrt{(1-\hat \beta _t)}·z_t xt=β^t⋅x0+(1−β^t)⋅zt
β t β_t βt的属性:为 ( β t ) t = 1 T (\beta_t)_{t=1}^T (βt)t=1T表示方差调度参数,根据论文描述 ( β t ) t = 1 T (\beta_t)_{t=1}^T (βt)t=1T介于 β 1 = 1 0 − 4 和 β T = 2 ⋅ 1 0 − 2 \beta_1=10^{-4}和\beta_T = 2·10^{-2} β1=10−4和βT=2⋅10−2之间其中 T = 1000。
反向过程
DDPMs的反向过程主要涉及如何根据给定的初始样本 x T ∼ N ( 0 , I ) x_T ∼ N(0,I) xT∼N(0,I),按照逆向步骤 p ( x t − 1 ∣ x t ) = N ( x t − 1 ; μ ( x t , t ) , ∑ ( x t , t ) ) p(x_{t-1}|x_t) = N(x_{t-1};μ(x_t ,t),\sum(x_t,t)) p(xt−1∣xt)=N(xt−1;μ(xt,t),∑(xt,t))生成新的样本。
首先,描述一下整个反向生成过程:
- 输入:
-
- T - 扩散步骤的数量。
-
- σ 1 , . . . , σ T σ_1,...,σ_T σ1,...,σT - 反向转换的标准差。
- 输出:
-
- x 0 x_0 x0 - 生成的图像样本。
- 计算过程:
-
- 3.1 从标准正态分布中抽取样本: x T ∼ N ( 0 , I ) x_T∼N(0,I) xT∼N(0,I)。
-
- 3.2 从 T T T步开始逆向迭代直到第 1 步:
-
-
- 如果 t > 1 t>1 t>1,抽取 z ∼ N ( 0 , I ) z∼N(0,I) z∼N(0,I)。
-
-
-
- 否则,令 z = 0 z=0 z=0。
-
-
-
- 计算均值 μ θ μ_θ μθ: μ θ = 1 α t ( x t − 1 − α t 1 − β ^ t ⋅ z θ ( x t , t ) ) μ_θ=\sqrt{\frac{1}{α_t}}(x_t-\sqrt{\frac{1-α_t}{1-\hat \beta_t}}·z_θ(x_t,t)) μθ=αt1(xt−1−β^t1−αt⋅zθ(xt,t))
-
-
-
- 生成样本 x t − 1 x_{t−1} xt−1: x t − 1 = μ θ + σ t ⋅ z x_{t-1} = μ_θ+σ_t ·z xt−1=μθ+σt⋅z
- 生成样本 x t − 1 x_{t−1} xt−1: x t − 1 = μ θ + σ t ⋅ z x_{t-1} = μ_θ+σ_t ·z xt−1=μθ+σt⋅z
-
这个过程通过使用逆向迭代和生成式来产生一个新的样本 x 0 x_0 x0
,它是从 T T T步开始逆向推断过程中生成的最终样本。
噪声条件得分网络(NCSNs)
噪声条件得分网络将数据密度 p ( x ) p(x) p(x)改为相对输入的对数密度的梯度 ∇ x l o g p ( x ) ∇_xlogp(x) ∇xlogp(x)。这些梯度给出的方向被 Langevin 动力学算法定义为用于从随机样本 ( x 0 ) (x_0) (x0) 移动到高密度区域的样本 ( x N ) (x_N) (xN)的方向。
Langevin 动力学是一种受物理学启发的迭代方法,可用于数据采样。在物理学中,该方法用于确定分子系统中粒子的轨迹,允许粒子与其他分子之间发生相互作用。粒子的轨迹受系统的阻力力和由分子之间的快速相互作用引起的随机力的影响。
在算法这里,我们可以将对数密度的梯度视为一种力,将随机样本通过数据空间拖向高数据密度 p ( x ) p(x) p(x) 的区域。
另外用 ω i ω_i ωi表示物理学中的随机力, γ γ γ值表示这两种力的影响,因为它代表粒子所处环境的摩擦系数。
从采样的角度看, γ γ γ控制更新的幅度。
通过训练 NCSNs 模型,我们可以有效地估计给定噪声尺度下的得分。在采样过程中,通过 Annealed Langevin dynamics 过程,模拟粒子在势能场中的运动,从而生成样本。整个框架通过对不同噪声水平下的数据建模,使得模型更具鲁棒性,能够处理数据中的不同特征和模式。
Langevin 动力学的迭代目标函数更新如下:
x i = x i − 1 + γ 2 ∇ x l o g p ( x ) + γ ⋅ w i x_i = x_{i-1}+\frac{γ}{2}∇_xlogp(x)+\sqrt{γ}·w_i xi=xi−1+2γ∇xlogp(x)+γ⋅wi
其中 i ∈ [ 1 , . . . , N ] i \in [1,...,N] i∈[1,...,N], γ γ γ控制更新在得分方向的幅度, x 0 x_0 x0 从先验分布中采样,噪声 w i ∼ N ( 0 , I ) w_i ∼N(0,I) wi∼N(0,I)解决了陷入局部最小值的问题,该方法递归地应用于 N → ∞ N→∞ N→∞步,
因此生成模型可以使用上述方法从 p ( x ) p(x) p(x)中采样,先通过神经网络 s θ ( x ) s_θ(x) sθ(x)估计得分 ∇ x l o g p x ( x ) ∇_xlogpx(x) ∇xlogpx(x)。
该网络可以通过分数匹配进行训练,就需要优化损失函数:
L s m = E x ∼ p ( x ) ∣ ∣ s θ ( x ) − ∇ x l o g p x ( x ) ∣ ∣ 2 2 L_{sm} = E_{x∼p(x)}||s_θ(x) -∇_xlog px(x) ||_2^2 Lsm=Ex∼p(x)∣∣sθ(x)−∇xlogpx(x)∣∣22
正向过程
初始化
给定一个高斯噪声尺度序列 σ 1 < σ 2 < … < σ T σ_1 <σ_2<…<σ_T σ1<σ2<…<σT使得 p σ 1 ( x ) ≈ p ( x 0 ) p_{σ_1}(x)≈p(x _0) pσ1(x)≈p(x0)和 p σ T ( x ) ≈ N ( 0 , I ) p_{σ_T(x)}≈N(0,I) pσT(x)≈N(0,I),
训练 NCSNs
可以使用去噪分数匹配训练一个 NCSN s θ ( x , σ t ) s_θ(x,σ_t) sθ(x,σt),使得 s θ ( x , σ t ) ≈ ∇ x l o g ( p σ t ( x ) ) s_θ(x,σ_t )≈∇_xlog(p_{σ_t}(x)) sθ(x,σt)≈∇xlog(pσt(x)),对于所有 t ∈ [ 1 , . . . , T ] t∈[1,...,T] t∈[1,...,T]。可以推导 ∇ x l o g ( p σ t ( x ) ) ∇_xlog(p_{σ_t}(x)) ∇xlog(pσt(x)) 如下:
∇ x t l o g p σ t ( x t ∣ x ) = − x t − x σ t 2 ∇_x^tlogp_{σ_t}(x_t|x)=-\frac{x_t-x}{σ_t^2} ∇xtlogpσt(xt∣x)=−σt2xt−x
鉴于:
p σ t ( x t ∣ x ) = N ( x t ; x , σ t 2 ⋅ I ) = 1 σ t ⋅ 2 π e x p ( − 1 2 ⋅ ( x t − x σ t ) 2 ) p_{σ_t}(x_t|x)=N(x_t;x,σ_t^2·I)=\frac{1}{σ_t·\sqrt{2π}}exp(-\frac{1}{2}·(\frac{x_t-x}{σ_t})^2) pσt(xt∣x)=N(xt;x,σt2⋅I)=σt⋅2π1exp(−21⋅(σtxt−x)2)
将$ ∇ x l o g ( p σ t ( x ) ) ∇_xlog(p_{σ_t}(x)) ∇xlog(pσt(x))带入到损失函数进行替换,得到如下:
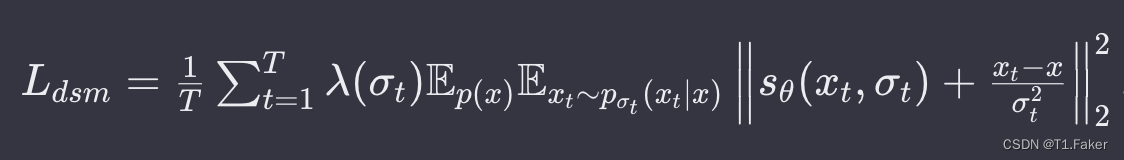
其中, λ ( σ t λ(σ_t λ(σt 是权重函数, p σ t p_{σ_t} pσt是给定噪声尺度 σ t σ_t σt 下的噪声分布。
生成样本
在推断时,采用 Annealed Langevin dynamics 过程生成样本。
反向过程
- 初始化: 使用白噪声生成初始样本 x 0 T ∼ N ( 0 , I ) x_0^T∼N(0,I) x0T∼N(0,I)。
- 迭代更新:从 t = T t=T t=T到 t = 1 t=1 t=1进行迭代,每一步包含 N N N次更新。对于每次更新 i = 1 , … , N i=1,…,N i=1,…,N,进行以下步骤:
-
- 2.1 从标准正态分布 N ( 0 , I ) N(0,I) N(0,I) 中采样噪声项 ω ω ω,即 ω ∼ N ( 0 , I ) ω∼N(0,I) ω∼N(0,I)
-
- 2.2 使用已训练的 NCSNs 模型 s θ ( x i − 1 t , σ t ) s_θ (x_{i−1}^t ,σ_t) sθ(xi−1t,σt) 估计得分。
-
- 2.3 根据 Langevin dynamics 更新规则,计算下一步样本 x i t : x i t = x i − 1 t + γ t 2 s θ ( x i − 1 t , σ t ) + γ t ω x_i^t:x_i^t=x_{i-1}^t +\frac{γ_t}{2}s_θ(x_{i-1}^t,σ_t)+\sqrt{γ_t}ω xit:xit=xi−1t+2γtsθ(xi−1t,σt)+γtω
-
- 2.4 保留每一步更新后的样本 x i t x_i^t xit。
- 返回结果: 返回 x 0 T − 1 x_0^{T−1} x0T−1 ,即最后一步的样本。
最后通过一段文字来解释为什么可以用Langevin 动力学来实现(NCSNs)
当我们试图从一个概率分布中采样样本时,尤其是高维空间中的复杂分布,这个过程可能非常具有挑战性。Langevin 动力学是一种仿照物理学中粒子在势能场中运动的方式的采样方法,这里的 “势能场” 实际上是指我们想要从中采样的概率分布。
想象一下,你是一颗微小的颗粒,漂浮在这个概率分布所定义的空间中。在物理学中,Langevin 动力学通常用于描述微粒在液体或气体中的运动,受到来自环境的阻力和随机碰撞的影响。类似地,在采样过程中,我们将你想象成这个微粒,而概率分布中的梯度(得分)则是指导你朝向高概率区域的力。
Langevin 动力学就像是你在一个由数据密度定义的山谷中滚动。梯度给出了你应该滚动的方向,而随机噪声则模拟了环境的不确定性和波动性。这种动力学确保了你不仅能够向概率分布的高密度区域移动,而且由于随机性,有时你也能够跳出局部最小值。
换句话说,通过仿效物理学中微粒在势场中的运动方式,Langevin 动力学提供了一种直观而生动的方式,使我们能够在概率分布中游走,从而采样到我们感兴趣的样本。在这个过程中,我们借助神经网络(NCSNs)来模拟概率分布的梯度,使得我们能够更有效地引导采样过程,特别是在处理不同噪声水平和复杂数据模式时。
随机微分方程(SDEs)
原理背景
随机微分方程(SDEs)方法类似于前述方法,如DDPMs和NCSNs,旨在通过将数据分布逐渐转化为噪声来进行采样。这种方法的独特之处在于它将扩散过程视为连续的,从而成为随机微分方程的解。具体而言,该方法在生成过程中使用了正向扩散SDE和逆向扩散SDE。正向扩散过程模拟了从初始数据分布 p ( x 0 ) p(x_0) p(x0)逐渐过渡到噪声的过程。
正向过程
正向扩散过程的SDE表达式为:
∂ t ∂ x = f ( x , t ) + σ ( t ) ⋅ ω t \frac{∂t}{∂x}=f(x,t)+σ(t)⋅ω_t ∂x∂t=f(x,t)+σ(t)⋅ωt
其中, ω t ω_t ωt是高斯噪声, f f f是计算漂移系数的函数, σ σ σ是计算扩散系数的时间相关函数。这个过程的目标是通过设计漂移系数,逐渐减小数据 x 0 x_0 x0,同时通过扩散系数控制添加的高斯噪声的程度。
反向过程
与正向过程对应的逆向SDE表示为:
∂ t ∂ x = f ( x , t ) − σ ( t ) 2 ⋅ ∇ x l o g p t ( x ) ⋅ ∂ t + σ ( t ) ⋅ ∂ ω \frac{∂t}{∂x} =f(x,t)− \frac{σ(t)}{2} ⋅∇xlogp_t (x)⋅∂t+σ(t)⋅∂ω ∂x∂t=f(x,t)−2σ(t)⋅∇xlogpt(x)⋅∂t+σ(t)⋅∂ω
反向过程的关键在于逐步去除导致数据破坏的漂移项。这是通过减去 σ ( t ) 2 ⋅ ∇ x l o g p t ( x ) \frac{σ(t)}{2}·∇x log p_t(x) 2σ(t)⋅∇xlogpt(x)来实现的。
模型训练与采样
为了实现这一过程,Song等人的生成模型利用神经网络估计得分函数,通过数值SDE求解器从 p ( x 0 ) p(x_0) p(x0)生成样本。神经网络 s θ ( x , t ) s_θ(x, t) sθ(x,t)接收扰动数据和时间步长作为输入,并生成对得分函数的估计。
训练时,使用了连续情况下的目标函数:
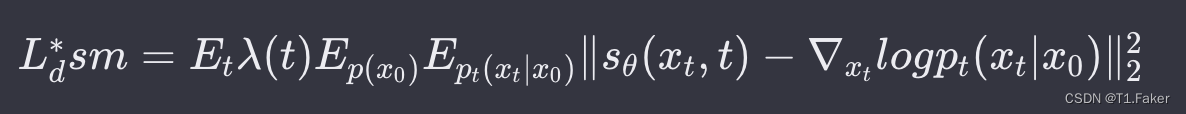
其中,λ是权重函数, t ∼ U ( [ 0 , T ] ) t ∼ U([0, T]) t∼U([0,T])。
采样方法
采样过程采用Euler-Maruyama采样方法,通过数值方法求解逆向SDE。在实践中,数值求解器通常不适用于连续公式,因此使用了Euler-Maruyama方法,通过固定微小负步长 Δ t \Delta t Δt执行采样过程。采样过程中的布朗运动由 Δ ω ^ = ∣ Δ t ∣ ⋅ z \Delta \hat{ω} = \sqrt{|\Delta t|} · z Δω^=∣Δt∣⋅z给出,其中 z ∼ N ( 0 , I ) z ∼ N(0, I) z∼N(0,I)。
方法可行性解释
该方法的可行性在于通过对数据密度的漂移和扩散过程的连续建模,成功地将数据逐渐转化为噪声。神经网络的引入提高了模型的表达能力,使其能够学习和逼近复杂的分布。采样过程中的数值方法确保了实际可行性,并通过改进的采样技术进一步提高了样本的质量。整体而言,该方法通过巧妙的数学建模和神经网络的结合,成功地实现了高质量样本的生成。
相关文章:
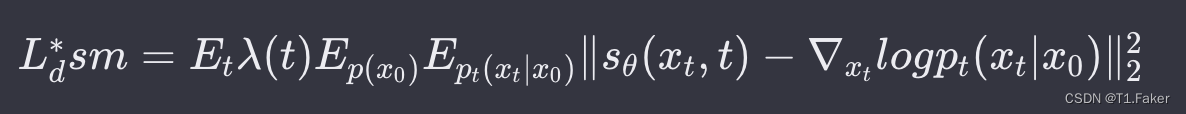
探索三种生成模型:基于DDPMs、NCSNs和SDEs方法的Diffusion
探索三种生成模型:基于DDPMs、NCSNs和SDEs方法的Diffusion 去噪扩散概率模型(DDPMs)正向过程反向过程 噪声条件得分网络(NCSNs)正向过程初始化训练 NCSNs生成样本 反向过程 随机微分方程(SDEs)原…...
)
Linux随记(七)
一、欧拉bclinux 21.10安装zabbix-5.0.37.tar.gz (zbx-客户端) #系统环境: BigCloud Enterprise Linux For Euler 21.10 LTS #软件信息: zabbix-5.0.37.tar.gz , pcre-devel-8.44-2.oe1.x86_64.rpm , inst…...

RESTful API,以及如何使用它构建 web 应用程序。
RESTful API是一种基于REST(Representational State Transfer)架构风格的API(Application Programming Interface),它采用HTTP协议中的GET、POST、PUT、DELETE等方法,对资源进行操作。RESTful API的核心思想…...
【华为OD题库-075】拼接URL-Java
题目 题目描述: 给定一个url前缀和url后缀,通过,分割。需要将其连接为一个完整的url。 如果前缀结尾和后缀开头都没有/,需要自动补上/连接符 如果前缀结尾和后缀开头都为/,需要自动去重 约束:不用考虑前后缀URL不合法情况 输入描述: url前缀(一个长度小于…...
【Unity动画】为一个动画片段添加事件Events
动画不管播放到那一帧,我们都可以在这里“埋伏”一个事件(调用一个函数并且给函数传递一个参数,参数在外部设置,甚至传递一个物体)! 嗨,亲爱的Unity小伙伴们!你是否曾想过为你的动画…...
CoDeF视频处理——视频风格转化部署使用与源码解析
一、算法简介与功能 CoDef是作为一种新型的视频表示形式,它包括一个规范内容场,聚合整个视频中的静态内容,以及一个时间变形场,记录了从规范图像(即从规范内容场渲染而成)到每个单独帧的变换过程。针对目标…...

ubuntu server 20.04 备份和恢复 系统 LTS
ubuntu server 20.04 备份和恢复 系统 LTS tar命令系统备份与恢复(还原or新装) 备份系统 cd / su root tar cvpzf backup.tgz --exclude/tmp --exclude/run --exclude/dev --exclude/snap --exclude/proc --exclude/lostfound --exclude/backup.tgz …...

NFC对物联网开发的影响及用途
当谈到NFC对物联网的影响时,不得不提它的几个重要的优势,可能在未来几年影响着物联网的发展方向。 全球智能手机的普及是其中一个重要因素:市面上已有数十亿部支持NFC的智能手机,专家们相信这个数字还会大幅增长。智能手机用户已…...
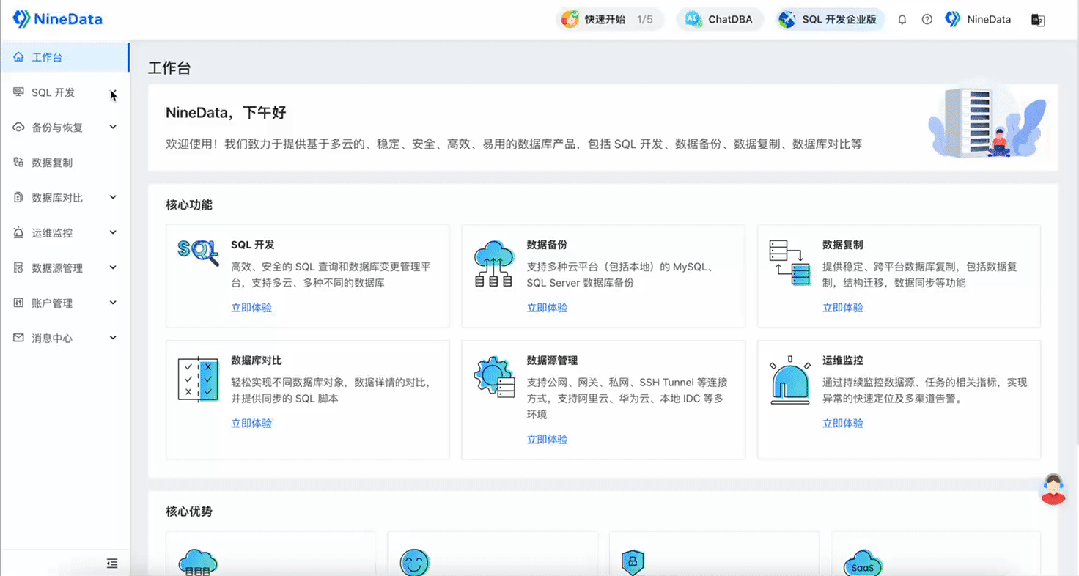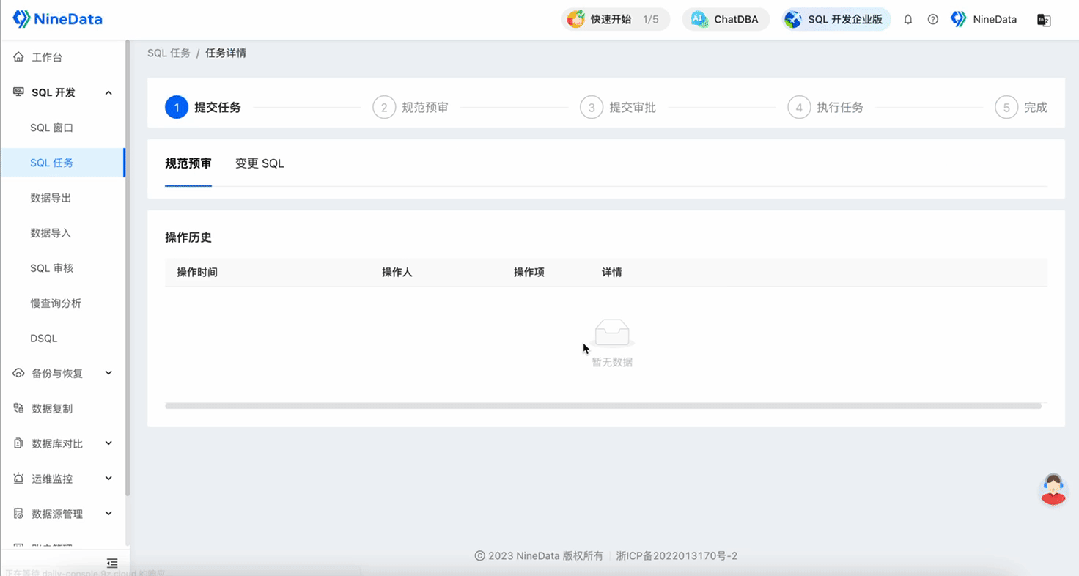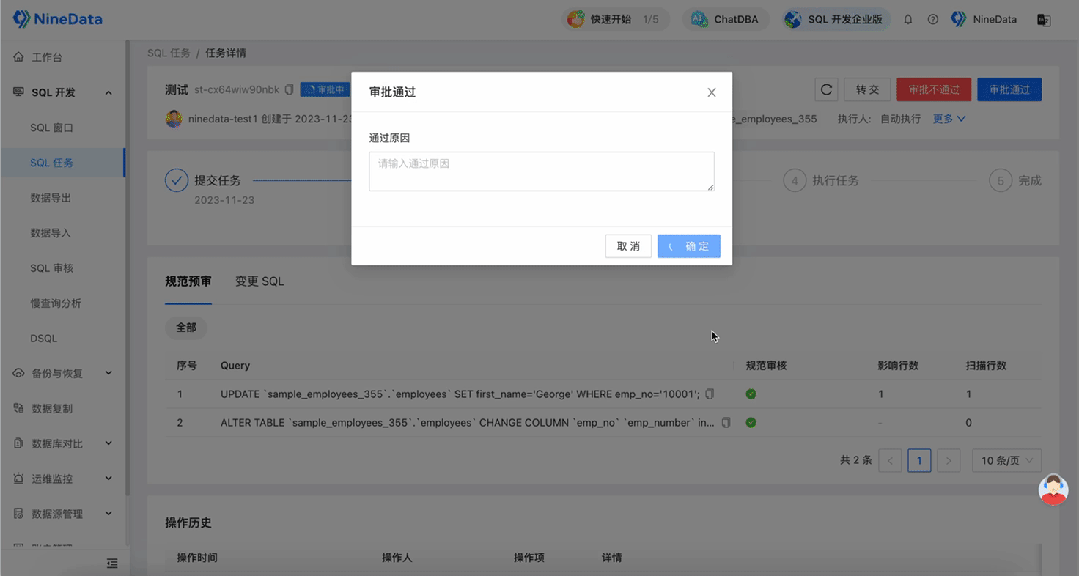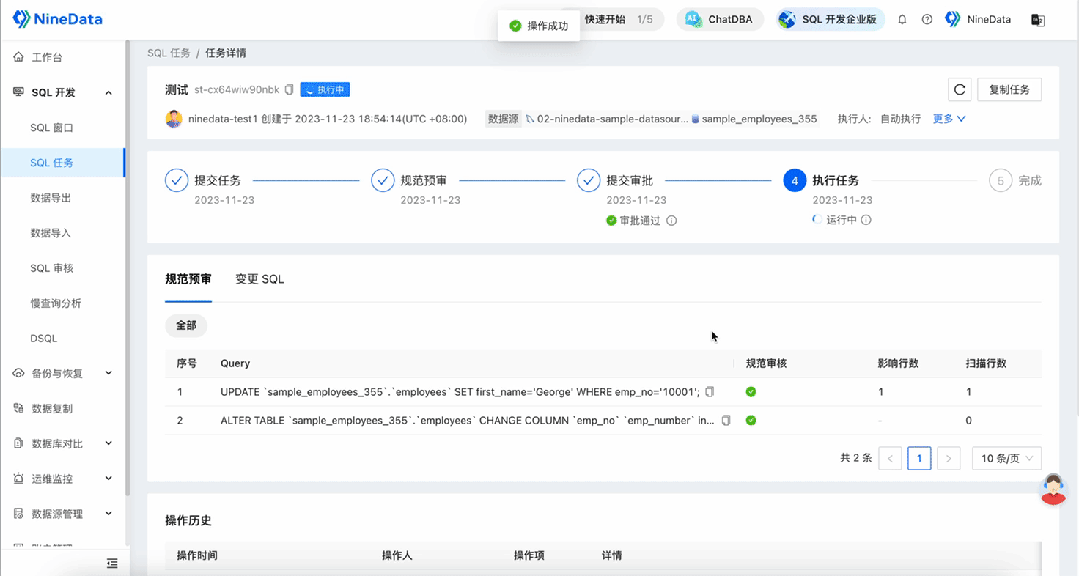
企业级SQL开发:如何审核发布到生产环境的SQL性能
自从上世纪 70 年代数据库开始普及以来,DBA 们就不停地遭遇各种各样的数据库管理难题,其中最为显著的,可能就是日常的开发任务中,研发人员们对于核心库进行变更带来的一系列风险。由于针对数据库的数据变更是一项非常常见的任务&a…...
linux 手动安装移植 haveged,解决随机数初始化慢的问题
文章目录 1、问题描述2、安装 haveged3、问题解决4、将安装好的文件跟库移植到开发板下 Haveged是一个软件工具,用于生成高质量的熵(Entropy)源,以供计算机系统使用。熵在计算机科学中指的是一种随机性或不可预测性的度量…...

如何使用llm 制作多模态
首先将任何非字符的序列信息使用特殊n个token 编码。 具体编码方法以图像为例子说明: 将固定尺寸图像如256256 的图像分割为1616 的子图像块。 将已知的所有图像数据都分割后进行str将其看做是一个长的字符,而后去重后方式一个词表。 使用特殊1024 个tok…...
:Pod)
k8s(二):Pod
Pod pod 是K8s中最小的可部署单元,用于容纳一个或多个容器。Pod为容器提供了一个共享的环境,包括网络命名空间、存储卷和IP地址。 pod的阶段(phase) Pending: Pod 已被 Kubernetes 系统接受,但有一个或者多个容器尚未创建亦未运行。此阶段包…...
)
Python 字典详解(dict)
文章目录 1 概述1.1 性质 2 常用方法2.1 以列表返回所有键:keys()2.2 以列表返回所有值:values()2.3 以列表返回所有键值对:items()2.4 返回键对应的值:get()2.5 添加键值对:setdefault()2.6 修改键值对:di…...

IPoIB在国产并行系统上的实现与优化
目录 1 国产异构众核系统 2 相关工作 3 IPoIB在国产并行系统上的实现 3.1 IPoIB协议原理...

东南大学与OpenHarmony携手共建开源生态,技术俱乐部揭牌成立并迎来TSC专家进校园
11月25日,OpenAtom OpenHarmony(以下简称“OpenHarmony”)项目群技术指导委员会(以下简称“TSC”)与东南大学携手,于东南大学九龙湖校区金智楼一楼报告厅举办了“东南大学OpenHarmony技术俱乐部成立仪式暨OpenHarmony TSC专家进校园”活动。此次盛会标志着OpenHarmony开源社区和…...

NPU、CPU、GPU算力及算力计算方式
NVIDIA在9月20日发布的NVIDIA DRIVE Thor 新一代集中式车载计算平台,可在单个安全、可靠的系统上运行高级驾驶员辅助应用和车载信息娱乐应用。提供 2000 万亿次浮点运算性能(2000 万亿次8位浮点运算)。NVIDIA当代产品是Orin,算力是…...
华清远见嵌入式学习——C++——作业6
作业要求: 代码: #include <iostream>using namespace std;class Animal { public:virtual void perform() 0;};class Lion:public Animal { private:string foods;string feature; public:Lion(){}Lion(string foods,string feature):foods(foo…...

k8s安装学习环境
目录 环境准备 配置hosts 关闭防火墙 关闭交换分区 调整swappiness参数 关闭setlinux Ipv4转发 时钟同步 安装Docker 配置Yum源 安装 配置 启动 日志 安装k8s 配置Yum源 Master节点 安装 初始化 配置kubectl 部署CNI网络插件 Node节点 检查 环境准备 准…...

RepidJson将内容写入文件简单代码示例
以下是使用RapidJSON将内容写入文件的示例代码: #include <rapidjson/document.h> #include <rapidjson/writer.h> #include <rapidjson/stringbuffer.h> #include <iostream> #include <fstream>using namespace rapidjson;int mai…...

golang构建docker镜像的几种方式
目前docker支持以下几种方式指定上下文来构建镜像 本地项目路径(如:/tmp/xxx)本地压缩包路径(如:/tmp/xxx.tar)docekrfile文本链接(如:https://x.com/xxx/dockerfile)压…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

沙箱虚拟化技术虚拟机容器之间的关系详解
问题 沙箱、虚拟化、容器三者分开一一介绍的话我知道他们各自都是什么东西,但是如果把三者放在一起,它们之间到底什么关系?又有什么联系呢?我不是很明白!!! 就比如说: 沙箱&#…...

CppCon 2015 学习:Time Programming Fundamentals
Civil Time 公历时间 特点: 共 6 个字段: Year(年)Month(月)Day(日)Hour(小时)Minute(分钟)Second(秒) 表示…...
