【视觉SLAM十四讲学习笔记】第三讲——四元数
专栏系列文章如下:
【视觉SLAM十四讲学习笔记】第一讲——SLAM介绍
【视觉SLAM十四讲学习笔记】第二讲——初识SLAM
【视觉SLAM十四讲学习笔记】第三讲——旋转矩阵
【视觉SLAM十四讲学习笔记】第三讲——旋转向量和欧拉角
本章将介绍视觉SLAM的基本问题之一:如何描述刚体在三维空间中的运动?
四元数
四元数的定义
旋转矩阵用9个量描述3自由度的旋转,具有冗余性;欧拉角和旋转向量是紧凑的,但具有奇异性。事实上,我们找不到不带奇异性的三维向量描述方式。类似于用两个坐标表示地球表面(如经度和纬度),必定存在奇异性(纬度为 ±90° 时经度无意义)。回忆以前学习过的复数。我们用复数集C表示复平面上的向量,而复数的乘法则表示复平面上的旋转:乘上复数i相当于逆时针把一个复向量旋转 90°。类似地,在表达三维空间旋转时,也有一种类似于复数的代数:四元数(Quaternion)。四元数是Hamilton找到的一种扩展的复数。它既是紧凑的,也没有奇异性。缺点是四元数不够直观,其运算稍复杂些。
把四元数与复数类比可以更快地理解四元数。例如,当我们想要将复平面的向量旋转 θ 角时,可以给这个复向量乘以 e^iθ。这是极坐标表示的复数,它也可以写成普通的形式,只要使用欧拉公式即可:
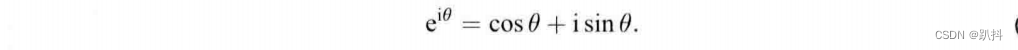
这是一个单位长度的复数。所以,在二维情况下,旋转可以由单位复数来描述。类似地,三维旋转则可以由单位四元数来描述。
一个四元数q拥有一个实部和三个虚部,示例如下:
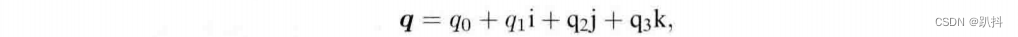
其中i,j,k为四元数的三个虚部。这三个虚部满足以下关系式:
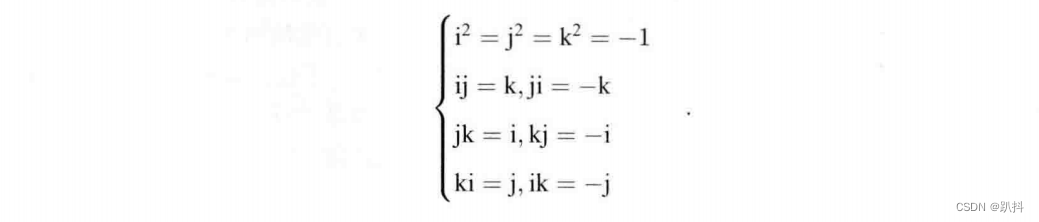
如果把i,j,k看成三个坐标轴,那么它们与自己的乘法和复数一样,相互之间的乘法和外积一样。有时人们也用一个标量和一个向量来表达四元数:
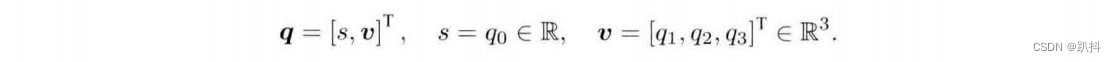
这里,s 称为四元数的实部,v称为它的虚部。如果一个四元数的虚部为0,称之为实四元数。反之,若它的实部为 0,则称之为虚四元数。
可以用单位四元数表示三维空间中任意一个旋转,不过这种表达方式和复数有些许不同。在复数中,乘以i意味着旋转 90°。这是否意味着四元数中,乘i就是绕i轴旋转90°?那么,ij=k是否意味着,先绕i转90°,再绕j转90°,就等于绕k转90°?
非也。应该是乘以i对应着旋转180◦,这样才能保证ij=k的性质。而i^2 = −1,意味着绕i轴旋转360°后得到一个相反的东西。这个东西要旋转两周(720°)才会和它原先的样子相等。(是不是很抽象)
四元数的运算
四元数常见的运算有四则运算、数乘、求逆、共轭等。
现在有两个四元数,原始表示为:
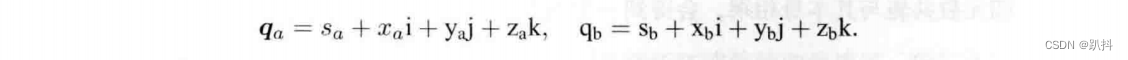
它们的向量表示为:
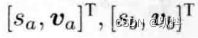
那么,其运算可表示如下:
-
加法和减法
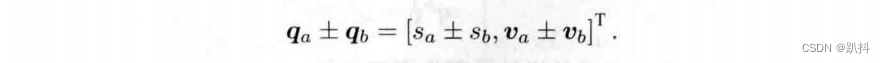
-
乘法
乘法是把qa的每一项和qb的每项相乘,最后相加:
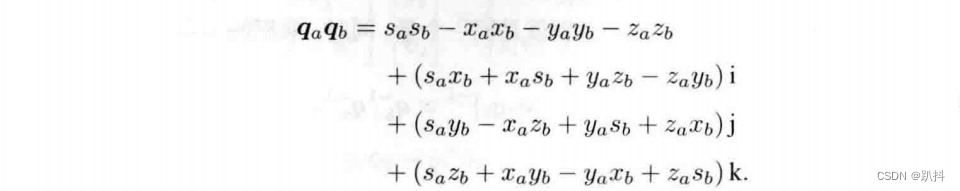
如果写成向量形式并利用内外积运算,该表达式会更加简洁:
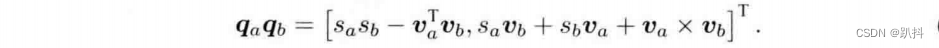
在该乘法定义下,两个实四元数乘积仍是实的,这与负数是一致的。然而我们注意到,由于最后一项外积的存在,四元数乘法通常是不可交换的,除非va和vb在R^3中共线,此时外积项为零。
-
模长
四元数的模长定义为
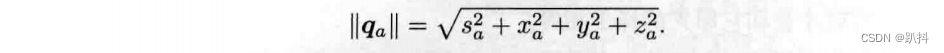
可以验证,两个四元数乘积的模即模的乘积。这使得单位四元数相乘后仍是单位四元数。
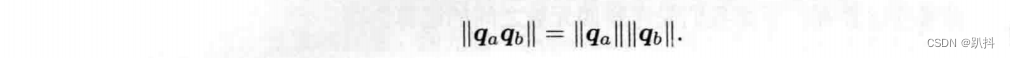
-
共轭
四元数的共轭是把虚部取成相反数:
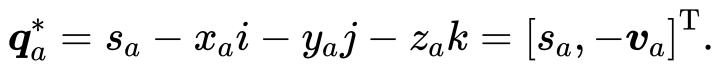
四元数共轭与其本身相乘,会得到一个实四元数,其实部为模长的平方:
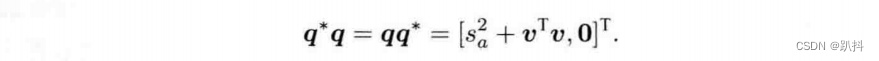
5. 逆
一个四元数的逆为
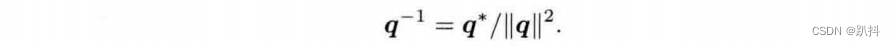
按此定义,四元数和自己的逆的乘积为实四元数1:
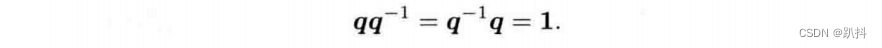
如果q为单位四元数,其逆和共轭就是同一个量。同时,乘积的逆具有和矩阵相似的性质:
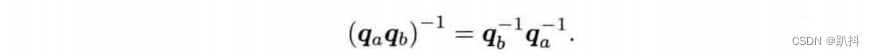
-
数乘
和向量相似,四元数可以与数相乘:
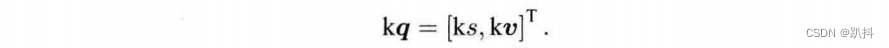
用四元数表示旋转
我们可以用四元数表达对一个点的旋转。假设有一个空间三维点
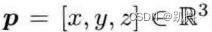
以及一个由单位四元数q指定的旋转。三维点p经过旋转之后变为p‘。如果使用矩阵描述,那么有p’=Rp。而如果用四元数描述旋转,它们的关系又如何表达呢?
首先,把三位空间点用一个虚四元数来描述:
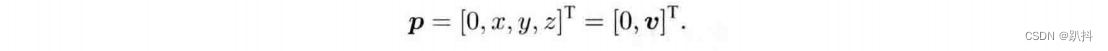
相当于把四元数的3个虚部与空间中的3个轴相对应。那么,旋转后的点p‘可表示为这样的乘积:
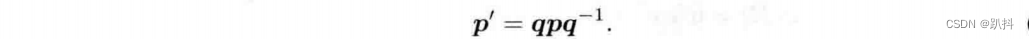
这里的乘法均为四元数乘法,结果也是四元数。最后把p’的虚部取出,即得旋转之后点的坐标。并且,计算结果的实部为0,故为纯虚四元数。
四元数到其他旋转表示的转换
任意单位四元数描述了一个旋转,该旋转也可用旋转矩阵或旋转向量描述。四元数乘法也可以写成一种矩阵的乘法。设q = [s,v]^T,那么,定义如下的符号 + 和 ⊕ 为:
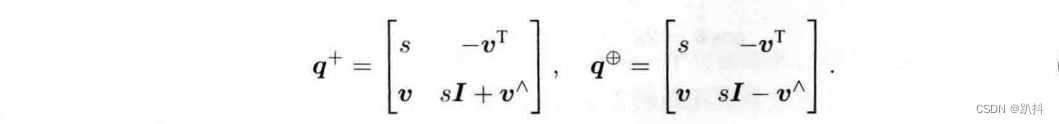
这两个符号将四元数映射成为一个 4×4 的矩阵。于是四元数乘法可以写成矩阵的形式:

同理亦可证:
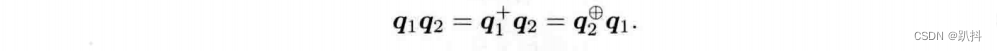
然后,考虑使用四元数对空间点进行旋转的问题:
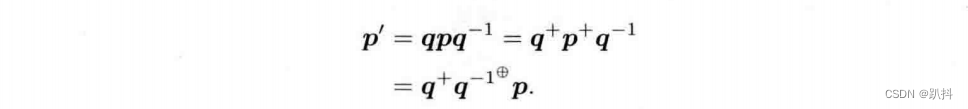
代入两个符号对应的矩阵,得:
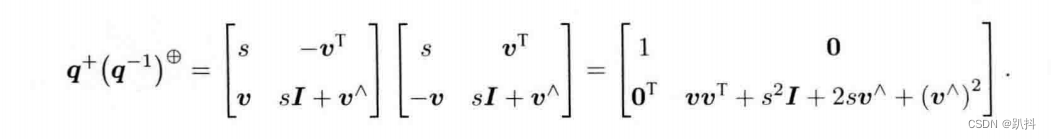
因为p′和p都是虚四元数,那么事实上该矩阵的右下角即给出了从四元数到旋转矩阵的变换关系:
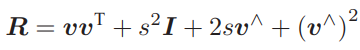
对上式两侧求迹,得:
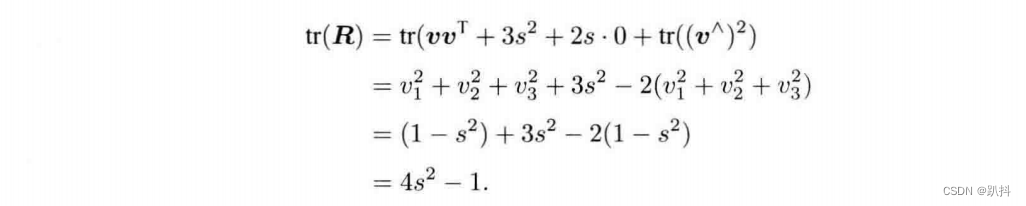
又由
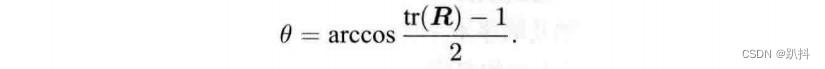
得到
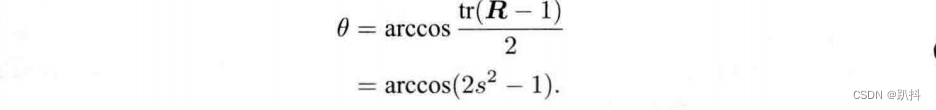
即
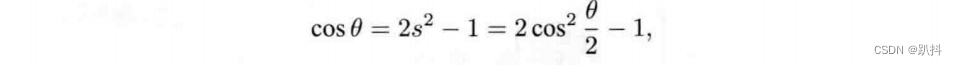
所以
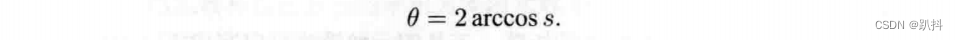
总而言之,四元数到旋转向量的转换公式如下:
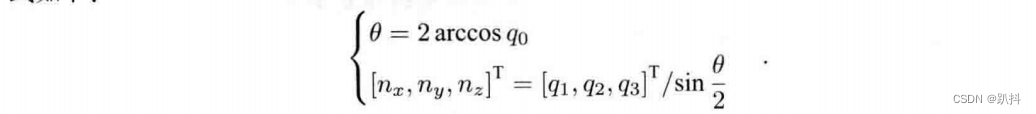
…(img-gkaQjiLn-1701177419079)]
代入两个符号对应的矩阵,得:
[外链图片转存中…(img-vQsuOEIL-1701177419080)]
因为p′和p都是虚四元数,那么事实上该矩阵的右下角即给出了从四元数到旋转矩阵的变换关系:
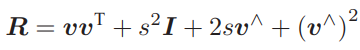
相关文章:
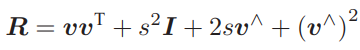
【视觉SLAM十四讲学习笔记】第三讲——四元数
专栏系列文章如下: 【视觉SLAM十四讲学习笔记】第一讲——SLAM介绍 【视觉SLAM十四讲学习笔记】第二讲——初识SLAM 【视觉SLAM十四讲学习笔记】第三讲——旋转矩阵 【视觉SLAM十四讲学习笔记】第三讲——旋转向量和欧拉角 本章将介绍视觉SLAM的基本问题之一&#x…...
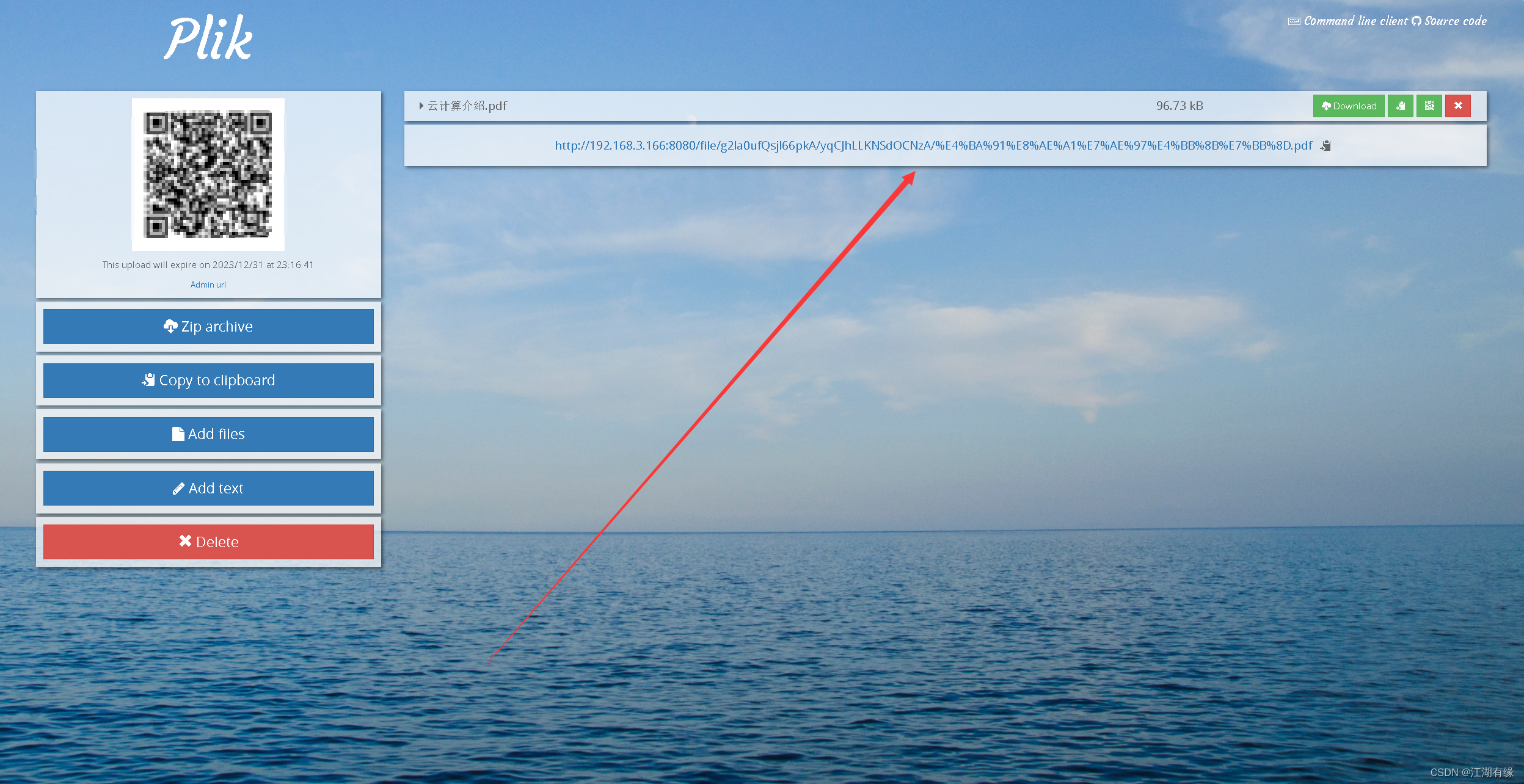
Linux系统之部署Plik临时文件上传系统
Linux系统之部署Plik临时文件上传系统 一、Plik介绍1.1 Plik简介1.2 Plik特点 二、本地环境介绍2.1 本地环境规划2.2 本次实践介绍 三、检查本地环境3.1 检查本地操作系统版本3.2 检查系统内核版本 四、下载Plik软件包4.1 创建下载目录4.2 下载Plik软件包4.3 查看下载的Plik软件…...
【EI征稿中#先投稿,先送审#】第三届网络安全、人工智能与数字经济国际学术会议(CSAIDE 2024)
第三届网络安全、人工智能与数字经济国际学术会议(CSAIDE 2024) 2024 3rd International Conference on Cyber Security, Artificial Intelligence and Digital Economy 第二届网络安全、人工智能与数字经济国际学术会议(CSAIDE 2023&…...
『亚马逊云科技产品测评』活动征文|基于亚马逊云EC2搭建OA系统
授权声明:本篇文章授权活动官方亚马逊云科技文章转发、改写权,包括不限于在 Developer Centre, 知乎,自媒体平台,第三方开发者媒体等亚马逊云科技官方渠道 亚马逊EC2云服务器(Elastic Compute Cloud)是亚马…...
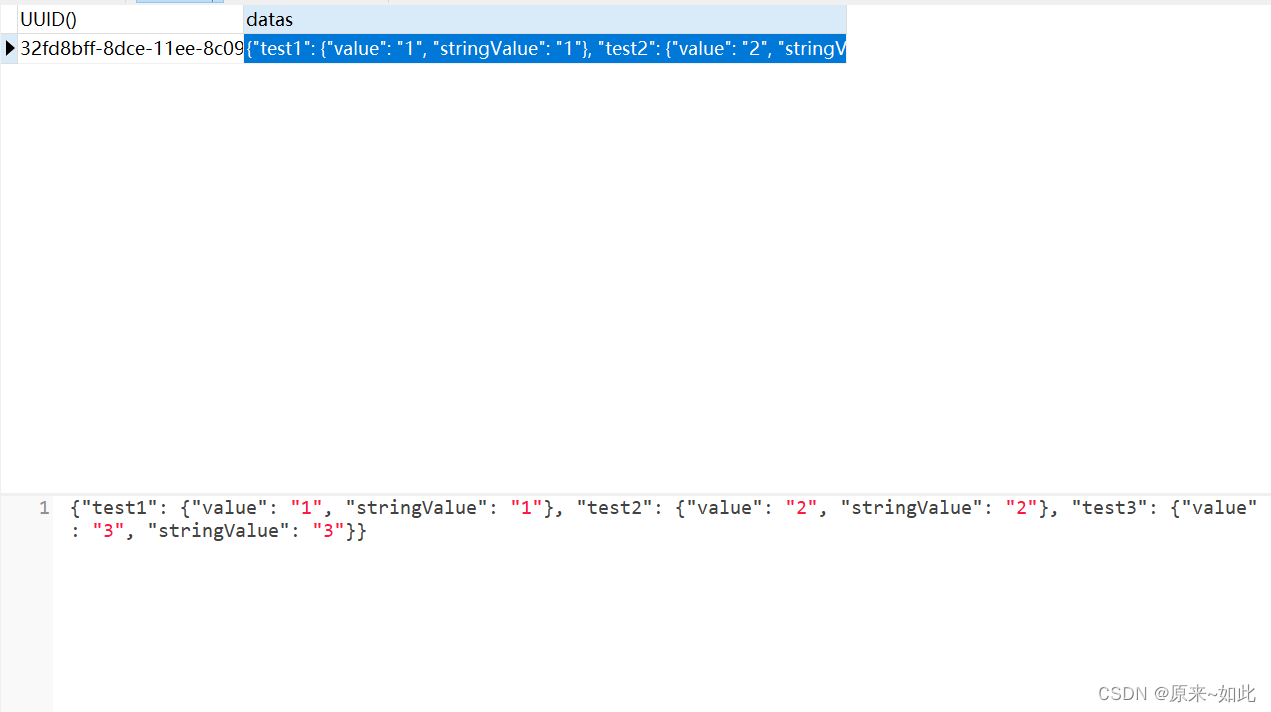
Mysql更新varchar存储的Josn数据
Mysql更新varchar存储的Josn数据 记录一次mysql操作varchar格式存储的json字符串数据 1、检查版本 -- 版本5.7以上才可以能执行json操作 select version(); 2、创建测试数据 -- 创建测试表及测试数据 CREATE TABLE test_json_table AS SELECT UUID(), {"test1": …...

JSON.stringify与JSON.parse详解与实践
目录 JSON.stringify 简介 主要用途: API 实践1: 实践2: JSON.parse 简介 API 实践1 实践2 JSON.stringify 简介 用于把JavaScript对象、数组、值、布尔值等序列化成字符串形式。 主要用途: 得到的数据通常有以下主…...

vue 基础
双向绑定的原理 双向绑定是一种数据绑定技术,它能够实现数据的自动同步更新,即当用户修改了数据时,界面也会随之自动更新,反之亦然。其原理如下: 数据模型:双向绑定的第一步是建立一个数据模型,…...

使用axios下载后端接口返回的文件流格式文件
在实际开发中,我们经常会遇到下载文件的需求,一般情况下接口最好的处理方式为上传到文件对象存储服务器,然后给前端返回一个下载文件的URL,前端直接打开链接下载就可以了,但…在下载数据量大且参数复杂的情况下&#x…...

在macOS上使用Homebrew安装PHP的完整指南
安装最新版本的PHP 步骤1: 安装Homebrew 在安装最新版本的PHP之前,确保你的macOS系统上已经安装了Homebrew。如果尚未安装,打开终端并运行以下命令: /bin/bash -c "$(curl -fsSL https://raw.githubusercontent.com/Homebrew/install…...

图片处理OpenCV IMDecode模式说明【生产问题处理】
OpenCV IMDecode模式说明【生产问题处理】 1 前言 今天售后同事反馈说客户使用我们的图片处理,将PNG图片处理为JPG图片之后,变为了白板。 我们图片处理使用的是openCV来进行处理 2 分析 2.1 图片是否损坏:非标准PNG头部 于是,马…...

吹响AI技术应用的号角
毫无疑问,各企业正围绕各种技术展开一场持续不断的角逐,力争率先取得领先且具创新性的技术进步,AI技术也不例外。疫情期间,全球各地企业的员工纷纷转向居家办公。因此,为轻松实现这一转型并建立起远程办公的新常态&…...

C //例10.1 从键盘输入一些字符,逐个把它们送到磁盘上去,直到用户输入一个“#”为止。
C程序设计 (第四版) 谭浩强 例10.1 例10.1 从键盘输入一些字符,逐个把它们送到磁盘上去,直到用户输入一个“#”为止。 IDE工具:VS2010 Note: 使用不同的IDE工具可能有部分差异。 代码块 方法:使用指针&…...
攻击与防御)
ARM预取侧信道(Prefetcher Side Channels)攻击与防御
目录 一、预取侧信道简介 1.1 背景:预取分类 二、Arm核会受到影响吗? 2.1 先进的预取器...
数据结构 | 二叉树的各种遍历
数据结构 | 二叉树的各种遍历 文章目录 数据结构 | 二叉树的各种遍历创建节点 && 创建树二叉树的前中后序遍历二叉树节点个数二叉树叶子节点个数二叉树第k层节点个数二叉树查找值为x的节点二叉树求树的高度二叉树的层序遍历判断二叉树是否是完全二叉树 我们本章来实现二…...

Python-赋值运算符(详解)
表示赋值 左侧为变量,右边为值 a b 10#先把10赋值给b,再把b赋值给a 相当于a 10 b 10 链式赋值,但是不推荐,一般一行一个语句,提高可读性,良好的代码风格 多元赋值: a , b 10,20 #python语…...

算法工程师面试八股(搜广推方向)
文章目录 机器学习线性和逻辑回归模型逻辑回归二分类和多分类的损失函数二分类为什么用交叉熵损失而不用MSE损失?偏差与方差Layer Normalization 和 Batch NormalizationSVM数据不均衡特征选择排序模型树模型进行特征工程的原因GBDTLR和GBDTRF和GBDTXGBoost二阶泰勒…...
)
学习TypeScrip4(数组类型)
数组的类型 1.定义方法:类型[ ] //类型加中括号 let arr:number[] [123] //这样会报错定义了数字类型出现字符串是不允许的 let arr:number[] [1,2,3,1] //操作方法添加也是不允许的 let arr:number[] [1,2,3,] arr.unshift(1)var arr: number[] [1, 2, 3]; /…...
Python文件打包成exe可执行文件
我们平常用python写些脚本可以方便我们的学习办公,但限制就是需要有python环境才能运行。 那能不能直接在没有python环境的电脑上运行我们的脚本呢? 当然可以,那就是直接把python脚本打包成exe可执行程序(注针对win系统…...
Android : SQLite 增删改查—简单应用
示例图: 学生实体类 Student.java package com.example.mysqlite.dto;public class Student {public Long id;public String name;public String sex;public int age;public String clazz;public String creatDate;//头像public byte[] logoHead;Overridepublic St…...

【蓝桥杯】马的遍历
马的遍历 题目描述 有一个 n m n \times m nm 的棋盘,在某个点 ( x , y ) (x, y) (x,y) 上有一个马,要求你计算出马到达棋盘上任意一个点最少要走几步。 输入格式 输入只有一行四个整数,分别为 n , m , x , y n, m, x, y n,m,x,y。 …...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...

沙箱虚拟化技术虚拟机容器之间的关系详解
问题 沙箱、虚拟化、容器三者分开一一介绍的话我知道他们各自都是什么东西,但是如果把三者放在一起,它们之间到底什么关系?又有什么联系呢?我不是很明白!!! 就比如说: 沙箱&#…...
