简介Kadane算法及相关的普通动态规划
简介Kadane算法及相关的普通动态规划
本文详细论述Kadane算法的经典题目,并通过“首先列出动态规划解法,再改为Kadane算法解法”的方式,讲解二者的不同。最后给出一道Kadane算法变体的题目,解法极为简洁优美。
Kadane算法也是一种动态规划算法,它的时间复杂度也是O(n), 但它与普通的动态规划有什么不同呢?这里先给出结论,不同就是:它的空间复杂度是O(1),而普通动态规划的空间复杂度是O(n).
下面的例题-1是一道经典的可以用Kadane算法求解的题目。
例题-1 LeetCode-53
给定一个整数数组,求它的子数组之和的最大值。
比如,数组为[-2,1,-3,4,-1,2,1,-5,4], 则子数组元素之和最大为6,因为当子数组为 [4,-1,2,1]时可取得最大值。
解法-1. 普通动态规划法
众所周知,动态规划法需要有一个递推公式。这个公式的思考与解析如下。
假设有一个同样大小的dp数组,其第i个位置的元素dp[i]的含义是:原整数数组s从0至i处且包含元素i时的所有子数组中子数组元素之和的最大值。
听见来很拗口是不是。说白了就是,对于所有的以s[i]为最右元素的子数组求子数组元素之和,最大的那个值就是dp[i].
想一想,如果我们知道了所有的dp[0], dp[1], …,dp[size-1], 那么我们是不是就知道了子数组之和的最大值了呢。
这里要注意的是,当 i < j < size 时, dp[i] 有可能大于 dp[j].
知道 dp[i] 的定义后,那么 dp[i+1] 是什么呢?
很明显,dp[i] 与 dp[i+1] 的差异就在于原数组的第 i+1 个元素,即 s[i+1].
一种可能是:s[i+1]可以被继续累加到当前最大值上,即dp[i]和s[i+1]都是非负数,那么 dp[i+1] = dp[i] + s[i+1]
另一种可能是:s[i+1]不可以被继续累加到当前最大值上, 比如:dp[i]是负数,而s[i+1]又比dp[i]大, 于是只好从s[i+1]开始算,即 dp[i+1] = s[i+1]
综合这2个式子:dp[i+1] = max(dp[i]+s[i+1], s[i+1])
换一种写法: dp[i] = max(dp[i-1]+s[i], s[i])
在当前定义下,我们最后需要返回 dp 数组中的最大元素。
这里有一个问题,为什么不能把 dp[i] 定义为“从0至i处的所有子数组中子数组元素之和的最大值”呢?
如果可以这么定义的话,那么我们就不需要在dp数组中找一个最大值,而只要返回dp数组的最后一个元素即可了。
其实对于有些问题时完全可以这么做的,比如下面的例题-2.
但是对于例题-1来说,鉴于其所求是子数组元素之和的最大值,它相当于对之前的多个元素有依赖关系,如果那样定义的话,则无法建立dp[i+1]和dp[i]之间的递推关系。
这个问题是一个隐藏较深且不太容易解释的问题。喜欢对算法作深入思考的朋友可以多想想这里,看是否有更加简洁精辟的见解。
普通动态规划法的代码还是比较简洁的,如下:
class Solution {public int maxSubArray(int[] nums) {int [] dp = new int [nums.length];dp[0] = nums[0];int result = nums[0];for (int i=1; i<nums.length; i++) {dp[i] = Math.max(nums[i], nums[i]+dp[i-1]);result = Math.max(result, dp[i]);}return result;}
}
解法-2. Kadane算法
上面的整个dp数组是否必要呢?
其实不是必要的。公式中的 dp[i] 和 dp[i-1] 看似不同,但其实可以巧妙地用一个变量来代表,从而整个dp数组也就不需要了 – 只用一个变量来维护dp[i]. 所以Kadane算法的空间复杂度是O(1). 这个技巧还是很值得学习的。
代码如下:
class Solution {public int maxSubArray(int[] nums) {int max_here = nums[0];int result = nums[0];for (int i=1; i<nums.length; i++) {max_here = Math.max(nums[i], nums[i]+max_here);result = Math.max(result, max_here);}return result;}
}
例题-1中对于dp[i]的定义还是不那么符合人的直觉的,而下面例题-2对 dp[i] 的设定则非常直接了。
例题-2. LeetCode-121
给定一个整数数组,其中每一个数字代表了股票在当天的价格。你每天只能操作一次,这一次是买或者卖股票,请最大化利润。
比如:[7,1,5,3,6,4],最大化利润是5. 因为在价格为1的那天买,在价格为6的那天卖,可以得到5的利润。
解法-1. 普通动态规划法
有了前面那么难的题,这题就简单了。对于动态规划,就是主要要考虑递推公式。
设定一个同样大小的数组dp,那么很自然地就想到 dp[i] 就代表到当天为止的最大利润。
那么dp[i+1]是什么呢? 假设原数组叫prices, 此时相当于多了一个 prices[i+1], 所引起的变化就是也许 prices[i+1] 能得到更高利润。
怎么会得到更高利润呢?如果用prices[i+1]减去之前的最小值,则是它得到的利润值;如果这个值比dp[i]大,则有了更高利润。
由此可见,要记录一个历史最小值。这个并不难实现。
这样一分析,递推公式就出来了: dp[i+1] = max(dp[i], prices[i+1]-minValue)
由此也可见,我们最后需要返回的就是 dp[size-1],即dp数组的最后一个元素。
普通动态规划法代码如下:
int maxProfit(vector<int>& prices) {if (prices.empty()) return 0;vector<int> dp(prices.size());dp[0] = 0;int minPrice = prices[0];for (int i=1; i<prices.size(); i++) {dp[i] = max(dp[i-1], prices[i] - minPrice);if (prices[i] < minPrice) minPrice = prices[i];}return dp[prices.size()-1];
}
解法-2. Kadane算法
仍然对普通动态规划法稍作优化,用一个变量代替dp[i]和dp[i+1], 由此消除dp数组。
代码如下:
int maxProfit(vector<int>& prices) {if (prices.empty()) return 0;int max_here = 0;int minPrice = prices[0];for (int i=1; i<prices.size(); i++) {max_here = max(max_here, prices[i] - minPrice);if (prices[i] < minPrice) minPrice = prices[i];}return max_here;
}
除了上面2道例题,有的时候会出现 Kadane 算法的变体。这个时候需要因为一些特殊条件而做出一些巧妙的变化,则可以继续使用Kadane算法。
例题-3 LeetCode-152
给定一个整数数组,求其子数组的乘积最大值。
比如:[2,3,-2,4],其子数组乘积最大值为6,因为 2x3=6.
首先,还是要找出递推数组。假设dp[i]为“至位置i处的包含了位置i的子数组乘积最大值”,那么对于例子中给定的数组,对应的dp数组是这样的:[2, 6, -2, 4]
所以, dp[i+1] = max(dp[i]*s[i+1], s[i])
由此似乎可以写出程序了。和例题-1很像嘛!是不是直接套就可以了?
但注意这样的数组: [-2, 3, -4], 很明显答案是24,但应用上面算法的dp数组是 [-2, 3, 3].
原因很简单,每遇到负数一次则结果反转,也就是说,如果应用了上面的算法,则-2无法被后面再一次遇到负数时用上。
换句话说,尽管dp[1]为3是正确的,但dp[2]还是3就不正确了,而此时dp[0]或原数组nums[0]的信息无法被dp[2]用上。
至此,普通的动态规划似乎不再能够应用了,因为递推关系似乎无法推出来。怎么办呢?其实Kadane算法仍可以应用。
鉴于负数每乘一次都会反转结果,我们就只好一直乘,直至结尾。如果负数的个数是偶数,则这就是结果(先不考虑0)。
但如果负数的个数是奇数,比如1个,那我们就不知道是在这个负数的左边还是右边会出现乘积最大值了。
这又怎么办呢?也很好办。从左往右和从右往左分别扫一遍。因为我们不可能在一遇到负数的时候就重启计算。
最后,一旦遇到0怎么办呢?这就要重启计算了。相当于数字0将数组分段了。一旦遇到0,则从0后面的第1个数字开始,重启我们的乘法运算,直至下一个0或数组在当前方向上结束。
啰里吧嗦说了很多,但代码其实还是很简洁的。
class Solution {public int maxProduct(int[] nums) {long r1 = Integer.MIN_VALUE;long p1 = 1;for (int i=0; i<nums.length; i++) {p1 = p1 * nums[i];if (p1 > r1) r1 = p1;if (p1 == 0) p1 = 1;}long r2 = Integer.MIN_VALUE;long p2 = 1;for (int i=nums.length-1; i>=0; i--) {p2 = p2 * nums[i];if (p2 > r2) r2 = p2;if (p2 == 0) p2 = 1;}return (int)(r1>r2?r1:r2);}
}
由本题可见,Kadane算法其实可能比普通动态规划更加灵活。
(END)
相关文章:

简介Kadane算法及相关的普通动态规划
简介Kadane算法及相关的普通动态规划 本文详细论述Kadane算法的经典题目,并通过“首先列出动态规划解法,再改为Kadane算法解法”的方式,讲解二者的不同。最后给出一道Kadane算法变体的题目,解法极为简洁优美。 Kadane算法也是一…...
校园教务管理系统
学年论文(课程设计) 题目: 信息管理系统 校园教务管理系统 摘要:数据库技术是现代信息科学与技术的重要组成部分,是计算机数据处理与信息管理系统的核心,随着计算机技术的发展,数据库技…...

【LeetCode热题100】【双指针】接雨水
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。 示例 1: 输入:height [0,1,0,2,1,0,1,3,2,1,2,1] 输出:6 解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] …...
)
软件工程-(可行性分析、需求分析)
目录 一.可行性研究 1.1定义 1.2项目背景 1.3三方面研究目标系统的可行性 1.3.1技术可行性分析 1.3.2 经济可行性分析 1.3.3 市场可行性分析 1.4. 数据流图 数据字典(DD) 1.5风险评估 1.6结论与建议 二、需求分析 引言 项目概述 利益相关者分析…...
HuggingFace学习笔记--BitFit高效微调
1--BitFit高效微调 BitFit,全称是 bias-term fine-tuning,其高效微调只去微调带有 bias 的参数,其余参数全部固定; 2--实例代码 from datasets import load_from_disk from transformers import AutoTokenizer, AutoModelForCaus…...

阅读笔记|A Survey of Large Language Models
阅读笔记 模型选择:是否一定要选择参数量巨大的模型?如果需要更好的泛化能力,用于处理非单一的任务,例如对话,则可用选更大的模型;而对于单一明确的任务,则不一定越大越好,参数小一…...
JSP 设置静态文件资源访问路径
这里 我们先在 WEB目录webapp 下创建一个包 叫 static 就用它来存静态资源 然后 我们扔一张图片进去 我们直接这样写 如下图 找到父级目录 然后寻找下面的 static 下的 img.png 运行代码 很明显 它没有找到 这边 我们直接找到 webapp目录下的 WEB-INF目录下的 web.xml 加入…...

【Pytorch】Visualization of Feature Maps(4)——Saliency Maps
学习参考来自 Saliency Maps的原理与简单实现(使用Pytorch实现)https://github.com/wmn7/ML_Practice/tree/master/2019_07_08/Saliency%20Maps Saliency Maps 原理 《Deep Inside Convolutional Networks: Visualising Image Classification Models and Saliency Maps》&…...
java第三十课
电商项目(前台): 登录接口 注册接口后台: 注册审核:建一个线程类 注意程序中的一个问题。 这里是 5 条记录,2 条记录显示应该是 3 页,实际操作过程 有审核机制,出现了数据记录动态变…...

Scala--2
package scala02object Scala07_typeCast {def main(args: Array[String]): Unit {// TODO 隐式转换// 自动转换val b: Byte 10var i: Int b 10val l: Long b 10 100Lval fl: Float b 10 100L 10.5fval d: Double b 10 100L 10.5f 20.00println(d.getClass…...
【SQL SERVER】定时任务
oracle是定时JOB,sqlserver是创建作业,通过sqlserver代理实现 先看SQL SERVER代理得服务有没有开 选择计算机右键——>管理——>服务与应用程序——>服务——>SQL server 代理 然后把SQL server 代理(MSSQLSERVER)启…...

MyBatis-Plus学习笔记(无脑cv即可)
1.MyBatis-Plus 1.1特性 无侵入:只做增强不做改变,引入它不会对现有工程产生影响,如丝般顺滑损耗小:启动即会自动注入基本 CURD,性能基本无损耗,直接面向对象操作强大的 CRUD 操作:内置通用 M…...

【VUE】watch 监听失效
如果你遇见了这个问题,那么尝试在 watch 函数中设置 { deep: true } 选项。这告诉 Vue 监听对象或数组内部的变化,就像下面这样: watch(()>chatStore.dataSources,(oldValue, newValue)>{// 监听执行逻辑 }, { deep: true })嗯&#x…...
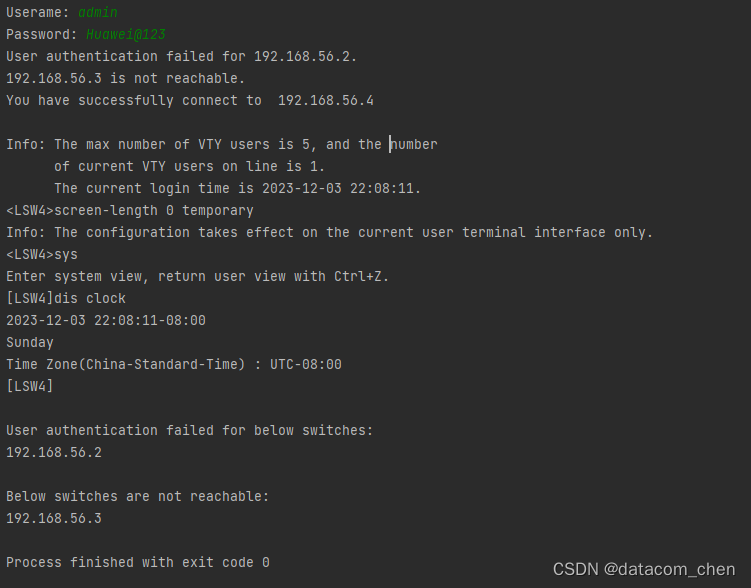
python的异常处理批量执行网络设备的巡检命令
前言 在网络设备数量超过千台甚至上万台的大型企业网中,难免会遇到某些设备的管理IP地址不通,SSH连接失败的情况,设备数量越多,这种情况发生的概率越高。 这个时候如果你想用python批量配置所有的设备,就一定要注意这…...
react native 环境准备
一、必备安装 1、安装node 注意 Node 的版本应大于等于 16,安装完 Node 后建议设置 npm 镜像(淘宝源)以加速后面的过程(或使用科学上网工具)。 node下载地址:Download | Node.js设置淘宝源 npm config s…...
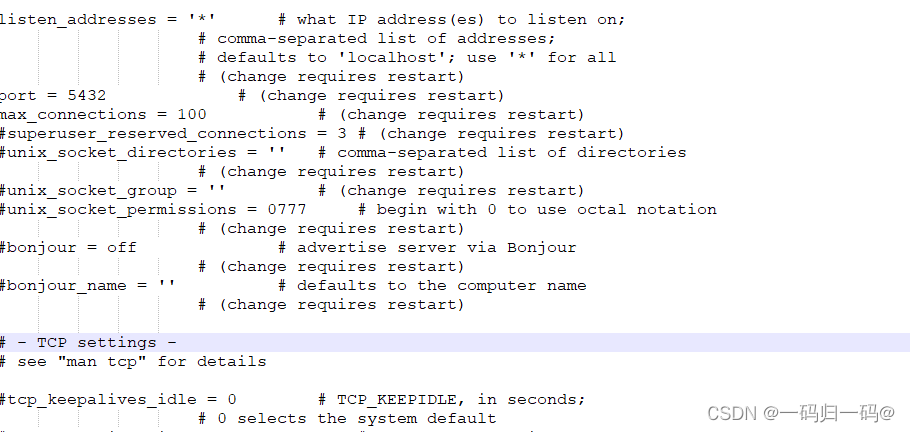
PGSQL(PostgreSQL)数据库安装教程
安装包下载 下载地址 下载后点击exe安装包 设置的data存储路径 设置密码 设置端口 安装完毕,配置PGSQL的ip远程连接,pg_hba.conf,postgresql.conf,需要更改这两个文件 pg_hba.conf 最后增加一行 host all all …...

识别和修复网站上损坏链接的最佳实践
如果您有一个网站,我们知道您花了很多时间在它上面,以使其成为最好的资源。如果你的链接不起作用,你的努力可能是徒劳的。您网站上的断开链接可能会以两种方式损害您的业务: 它们对企业来说是可怕的,因为当消费者点击…...

使用Navicat连接MySQL出现的一些错误
目录 一、错误一:防火墙未关闭 二、错误二:安全组问题 三、错误三:MySQL密码的加密方式 四、错误四:修改my.cnf配置文件 一、错误一:防火墙未关闭 #查看防火墙状态 firewall-cmd --state#关闭防…...
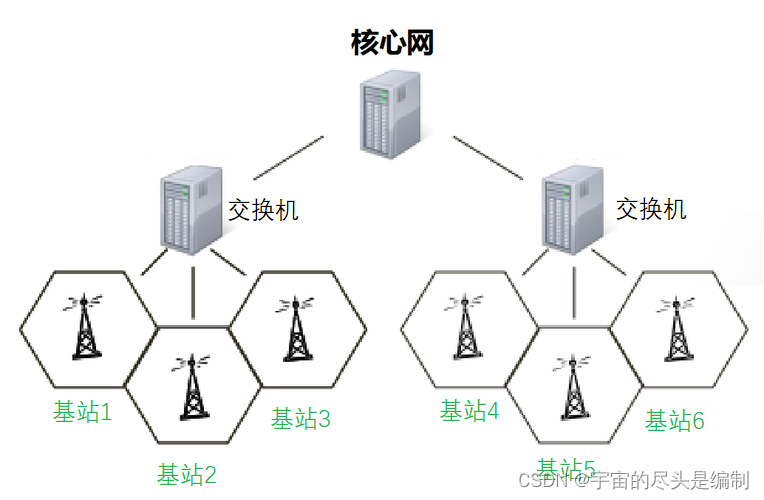
4G基站BBU、RRU、核心网设备
目录 前言 基站 核心网 信号传输 前言 移动运营商在建设4G基站的时候,除了建设一座铁塔之外,更重要的是建设搭载铁塔之上的移动通信设备,这篇博客主要介绍BBU,RRU以及机房的核心网等设备。 基站 一个基站有BBU,…...
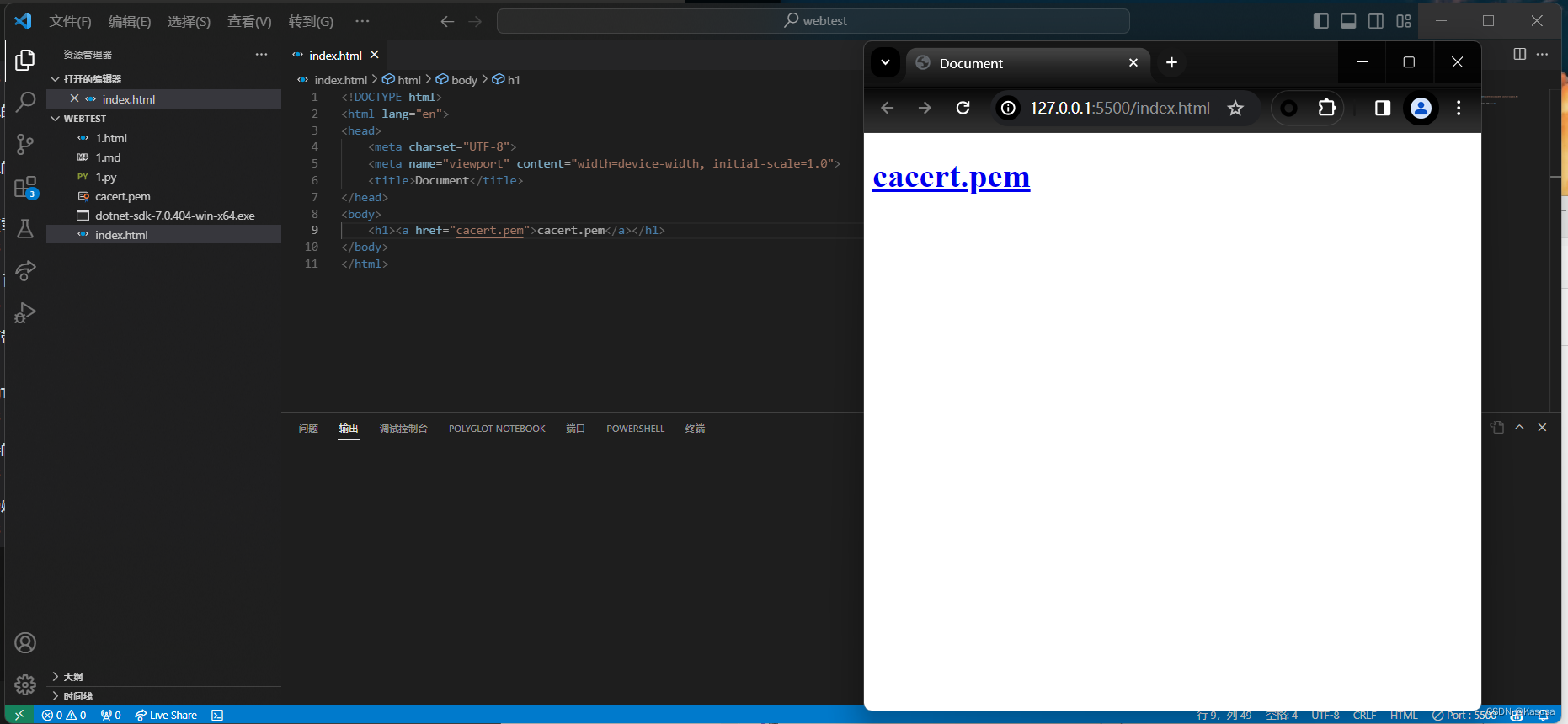
iphone/安卓手机如何使用burp抓包
iphone 1. 电脑 ipconfig /all 获取电脑网卡ip: 192.168.31.10 2. 电脑burp上面打开设置,proxy,增加一条 192.168.31.10:8080 3. 4. 手机进入设置 -> Wi-Fi -> 找到HTTP代理选项,选择手动,192.168.31.10:8080 …...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...
