openGauss学习笔记-146 openGauss 数据库运维-备份与恢复-配置文件的备份与恢复
文章目录
- openGauss学习笔记-146 openGauss 数据库运维-备份与恢复-配置文件的备份与恢复
- 146.1 背景信息
- 146.2 前置条件
- 146.3 操作步骤
- 146.4 示例
openGauss学习笔记-146 openGauss 数据库运维-备份与恢复-配置文件的备份与恢复
146.1 背景信息
在openGauss使用过程中,如果静态配置文件无意损坏后,会影响openGauss感知openGauss拓扑结构和主备关系。使用gs_om工具生成的静态配置文件,可以替换已经损坏的配置文件,保证openGauss的正常运行。
146.2 前置条件
无。
146.3 操作步骤
-
以操作系统用户omm登录数据库主节点。
-
执行如下命令会在本服务器指定目录下生成配置文件。
gs_om -t generateconf -X /opt/software/openGauss/clusterconfig.xml --distribute/opt/software/openGauss/clusterconfig.xml为openGauss安装时的XML配置文件。
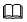 说明:
说明:- 执行命令后,日志信息中会有新文件的存放的目录。以一主两备环境为例,打开新文件存放目录,会出现3个以主机名命名的配置文件,需要用这3个文件分别替换对应主机的配置文件。
- 若不使用–distribute参数,需执行步骤3将静态配置文件分配到对应节点;若使用–distribute参数,则会将生成的静态配置文件自动分配到对应节点,无需执行步骤3。
-
(可选)分别替换3台主机的/opt/gaussdb/app/bin目录下损坏的静态配置文件。
这里以其中一台主机为例进行介绍。
mv /opt/huawei/wisequery/script/static_config_files/cluster_static_config_SIA1000056771 /opt/gaussdb/app/bin/cluster_static_config
146.4 示例
在openGauss中的任意主机上执行如下命令,生成配置文件:
gs_om -t generateconf -X /opt/software/openGauss/clusterconfig.xml --distribute
Generating static configuration files for all nodes.
Creating temp directory to store static configuration files.
Successfully created the temp directory.
Generating static configuration files.
Successfully generated static configuration files.
Static configuration files for all nodes are saved in /opt/huawei/Bigdata/mppdb/wisequery/script/static_config_files.
Distributing static configuration files to all nodes.
Successfully distributed static configuration files.
打开生成的配置文件目录,会看到新生成的3个文件:
cd /opt/huawei/Bigdata/mppdb/wisequery/script/static_config_files
ll
total 456
-rwxr-xr-x 1 omm dbgrp 155648 2016-07-13 15:51 cluster_static_config_plat1
-rwxr-xr-x 1 omm dbgrp 155648 2016-07-13 15:51 cluster_static_config_plat2
-rwxr-xr-x 1 omm dbgrp 155648 2016-07-13 15:51 cluster_static_config_plat3
👍 点赞,你的认可是我创作的动力!
⭐️ 收藏,你的青睐是我努力的方向!
✏️ 评论,你的意见是我进步的财富!

相关文章:

openGauss学习笔记-146 openGauss 数据库运维-备份与恢复-配置文件的备份与恢复
文章目录 openGauss学习笔记-146 openGauss 数据库运维-备份与恢复-配置文件的备份与恢复146.1 背景信息146.2 前置条件146.3 操作步骤146.4 示例 openGauss学习笔记-146 openGauss 数据库运维-备份与恢复-配置文件的备份与恢复 146.1 背景信息 在openGauss使用过程中&#x…...

一文读懂中间件
前言:在程序猿的日常工作中, 经常会提到中间件,然而大家对中间件的理解并不一致,导致了一些不必要的分歧和误解。“中间件”一词被用来描述各种各样的软件产品,在不同文献中有着许多不同的中间件定义,包括操…...

【编程基础心法】「设计模式系列」让我们一起来学编程界的“兵法”设计模式(序章)
一起来学编程界的“兵法”设计模式(序章) 设计模式是什么设计模式的概念设计模式的分类创建型模式(5种)结构型模式(7种)行为型模式(11种) 设计模式应用场景工厂模式的实现及应用单例…...

技术阅读周刊第第8️⃣期
技术阅读周刊,每周更新。 历史更新 20231103:第四期20231107:第五期20231117:第六期20231124:第七期 Prometheus vs. VictoriaMetrics (VM) | Last9 URL: https://last9.io/blog/prometheus-vs-victoriametrics/?refd…...

HTML程序大全(2):通用注册模版
一、正常情况效果 二、某项没有填写的效果 三、没有勾选同意项的效果 四、代码 <!DOCTYPE html> <html> <head><meta charset"UTF-8"><title>注册</title><style>body {font-family: Arial, sans-serif;background-color…...

【循环结构 for、break、continue高级用法】
在 C++ 中,for 循环是一种常用的循环结构,它用于重复执行代码块直到满足指定的条件。for 循环的基础用法相对简单,而高级用法则涉及更复杂的控制结构和技术。让我们探讨这些用法,并通过一些示例来加深理解。 文章目录 基础用法高级用法实战示例注意事项结合 break 和 conti…...
JAVA网络编程——BIO、NIO、AIO深度解析
I/O 一直是很多Java同学难以理解的一个知识点,这篇帖子将会从底层原理上带你理解I/O,让你看清I/O相关问题的本质。 1、I/O的概念 I/O 的全称是Input/Output。虽常谈及I/O,但想必你也一时不能给出一个完整的定义。搜索了谷哥欠,发…...

Linux高级系统编程-3 进程
概念 进程与程序的区别 程序:一个可执行文件, 占磁盘空间,是静态的 进程:一个程序运行的过程, 占内存,动态的。 单道程序和多道程序 单道程序设计: 所有进程一个一个排队执行。若 A 阻塞, B 只能等待࿰…...
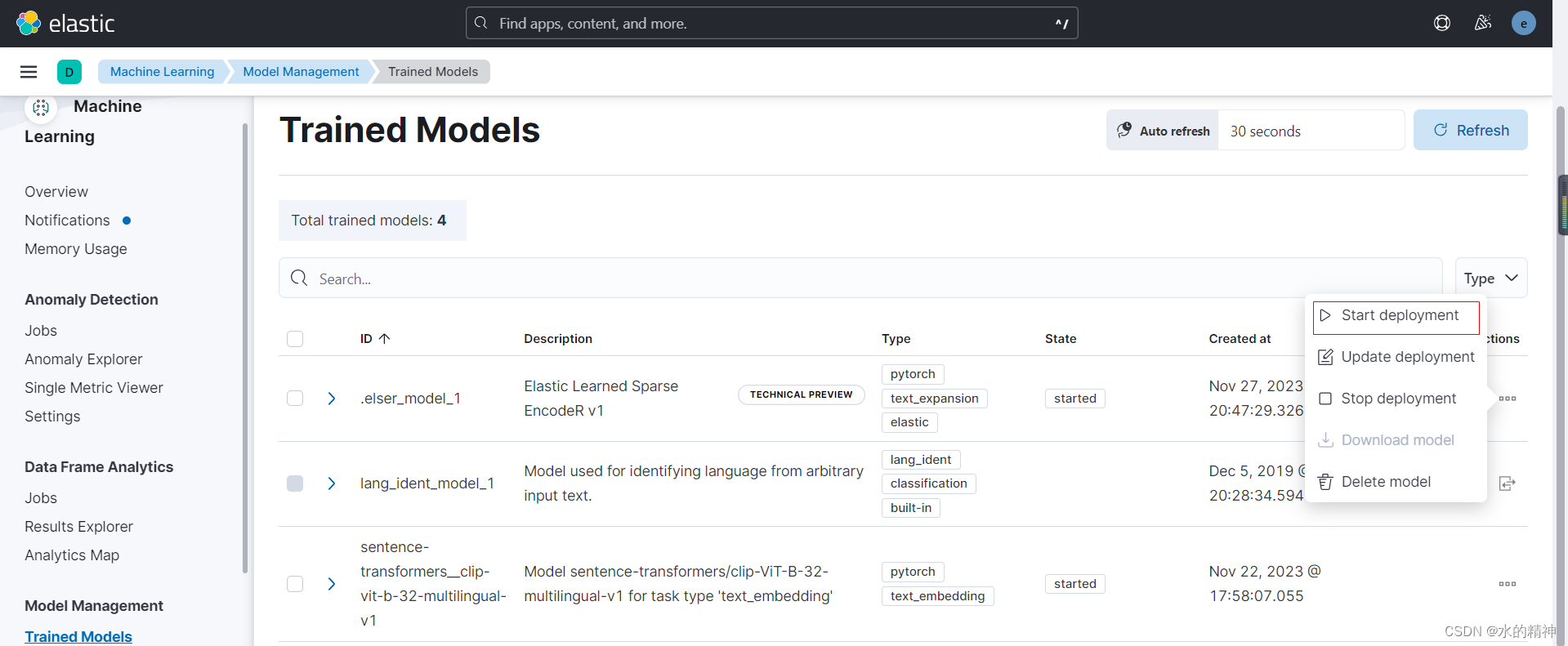
ES-ELSER 如何在内网中离线导入ES官方的稀疏向量模型(国内网络环境下操作方法)
ES官方训练了稀疏向量模型,用来支持语义检索。(目前该模型只支持英文) 最好是以离线的方式安装。在线的方式,在国内下载也麻烦,下载速度也慢。还不如用离线的方式。对于一般的生产环境,基本上也是网络隔离的…...

Excel 使用技巧
Excel 使用技巧 注意: excel 中设计计算的字符尽量使用英文。 拼接两段文字(字符串拼接) 方法一 在需要计算的单元格上,键入 点击 A1(点击需要拼接的单元格) & C1(点击需要拼接的单元格) 举例: 姓名栏想要拼接 姓 和 名 两列点击姓名这一…...
-Part.03 资源规划)
Hadoop学习笔记(HDP)-Part.03 资源规划
目录 Part.01 关于HDP Part.02 核心组件原理 Part.03 资源规划 Part.04 基础环境配置 Part.05 Yum源配置 Part.06 安装OracleJDK Part.07 安装MySQL Part.08 部署Ambari集群 Part.09 安装OpenLDAP Part.10 创建集群 Part.11 安装Kerberos Part.12 安装HDFS Part.13 安装Ranger …...

一个最新国内可用的免费GPT4,Midjourney绘画网站+使用教程
一、前言 ChatGPT GPT4.0,Midjourney绘画,相信对大家应该不感到陌生吧?简单来说,GPT-4技术比之前的GPT-3.5相对来说更加智能,会根据用户的要求生成多种内容甚至也可以和用户进行创作交流。 然而,GPT-4对普…...

深入了解Java8新特性-日期时间API之ZonedDateTime类
阅读建议 嗨,伙计!刷到这篇文章咱们就是有缘人,在阅读这篇文章前我有一些建议: 本篇文章大概19000多字,预计阅读时间长需要10分钟以上。本篇文章的实战性、理论性较强,是一篇质量分数较高的技术干货文章&…...

使用Vue写一个日期选择器
在 Vue 中实现日期选择器的方法有很多,下面提供一个简单的实现方法。 首先,在需要使用日期选择器的组件中引用 Vue 和 date-fns 库,date-fns 库是一个轻量级的 JavaScript 时间日期工具库,可以方便地处理日期的格式化和计算。 &…...

19、pytest通过mark标记测试函数
官方实例 [pytest] markers slow:marks tests as slow(deselect with -m "not slow")serial# content of test_mark.py import pytestpytest.mark.slow def test_mark_function():print("test_mark_function was invoked")assert 0解读与实操 通过使用p…...
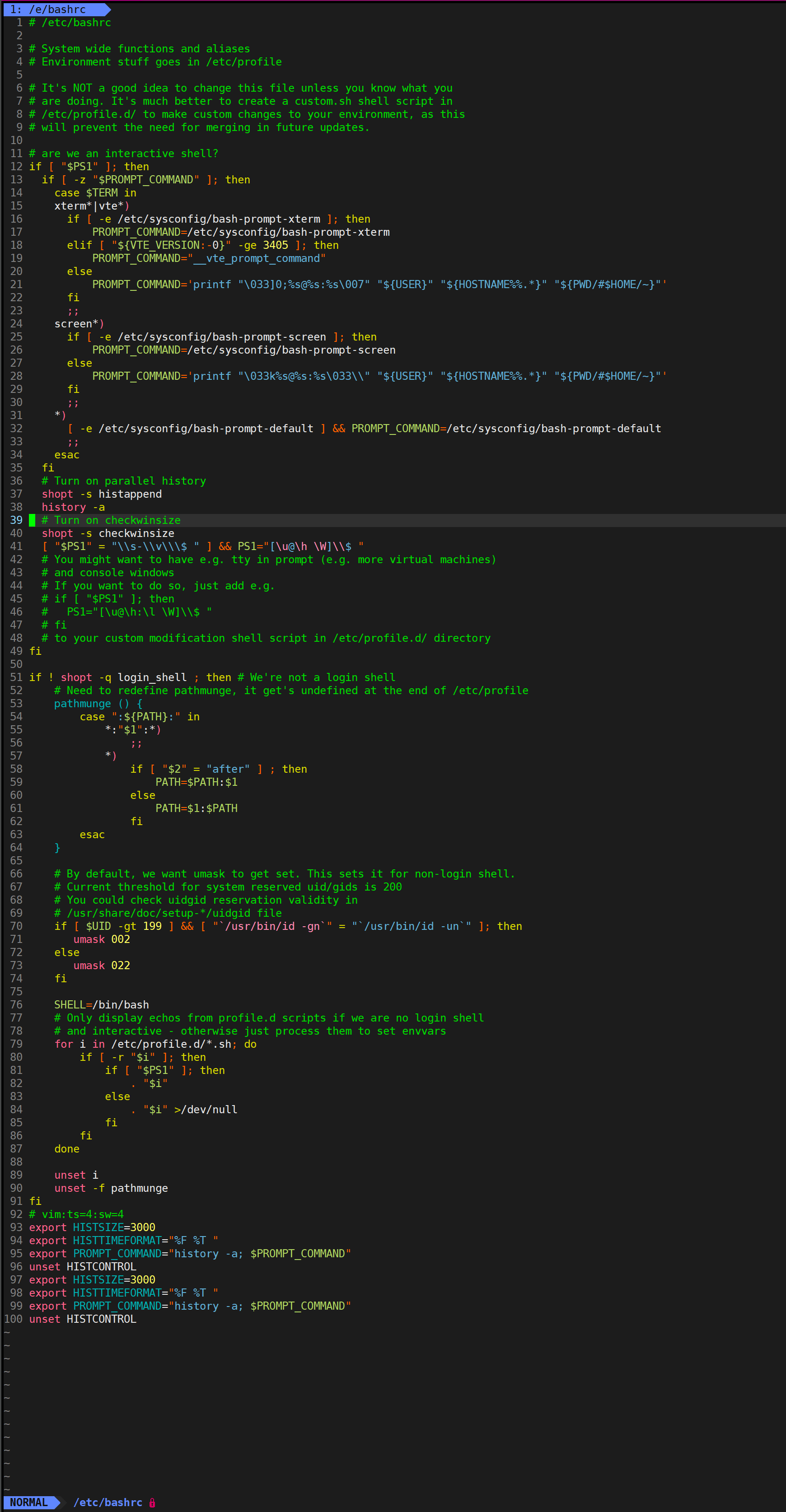
Linux环境变量与命令行参数
Linux环境变量与命令行参数 一.命令行参数1.语法2.应用1:简易计算器 二.环境变量1.环境变量的概念2.环境变量的作用3.进一步理解环境变量的作用4.常见环境变量5.导出环境变量(添加环境变量)6.环境变量的特性7.另一种获取环境变量的方式8.小功能:用于身份验证的代码9.补充:第三种…...

jQuery实现3D轮播图
通过CSS3的3D变换和jQuery Transit插件实现了一个3D旋转的图片轮播效果 HTML部分: div id“banner”:定义了一个id为"banner"的div标签,作为图片轮播的容器。 ul: 在"banner"中定义了一个无序列表,每个列表项…...
-------连载(43))
Java面试题(每天10题)-------连载(43)
目录 Spring篇 1、请举例说明Qualifier注解 2、构造方法注入和设值注入有什么区别? 3、Spring框架中有哪些不同类型的事件? 4、FileSystemResource和ClassPathResource有什么区别? 5、Spring框架中都用到了哪些设计模式? 6…...
)
Python高级数据结构——并查集(Disjoint Set)
Python中的并查集(Disjoint Set):高级数据结构解析 并查集是一种用于处理集合的数据结构,它主要支持两种操作:合并两个集合和查找一个元素所属的集合。在本文中,我们将深入讲解Python中的并查集࿰…...

pytorch学习9-优化器学习
系列文章目录 pytorch学习1-数据加载以及Tensorboard可视化工具pytorch学习2-Transforms主要方法使用pytorch学习3-torchvisin和Dataloader的使用pytorch学习4-简易卷积实现pytorch学习5-最大池化层的使用pytorch学习6-非线性变换(ReLU和sigmoid)pytorc…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...
