【矩阵论】Chapter 4—特征值和特征向量知识点总结复习
文章目录
- 1 特征值和特征向量
- 2 对角化
- 3 Schur定理和正规矩阵
- 4 Python求解
1 特征值和特征向量
-
定义
设 σ \sigma σ为数域 F F F上线性空间 V V V上的一个线性变换,一个非零向量 v ∈ V v\in V v∈V,如果存在一个 λ ∈ F \lambda \in F λ∈F使得 σ ( v ) = λ v \sigma(v)=\lambda v σ(v)=λv,则 λ \lambda λ称为 σ \sigma σ的特征值。 σ \sigma σ的特征值的集合称为 σ \sigma σ的谱。并称 v v v为 σ \sigma σ的属于(或对应于)特征值 λ \lambda λ的特征向量。
-
特征值和特征向量的求法
设 V V V是数域 F F F上的 n n n维线性空间, v 1 , ⋯ , v n v_1,\cdots,v_n v1,⋯,vn是 V V V的一组基,线性变换 σ \sigma σ在这组基下的矩阵为 A A A,如果 λ \lambda λ是 σ \sigma σ的特征值, α \alpha α是相应的特征向量。则
α = ( v 1 , ⋯ , v n ) ( x 1 ⋮ x n ) \alpha=(v_1,\cdots,v_n)\begin{pmatrix}x_1\\\vdots\\x_n\end{pmatrix} α=(v1,⋯,vn) x1⋮xn
将上式代入 σ ( v ) = λ v \sigma(v)=\lambda v σ(v)=λv得到
σ ( α ) = ( v 1 , ⋯ , v n ) A ( x 1 ⋮ x n ) λ α = λ ( v 1 , ⋯ , v n ) ( x 1 ⋮ x n ) \sigma(\alpha)=(v_1,\cdots,v_n)A\begin{pmatrix}x_1\\\vdots\\x_n\end{pmatrix}\\ \lambda \alpha=\lambda (v_1,\cdots,v_n)\begin{pmatrix}x_1\\\vdots\\x_n\end{pmatrix}\\ σ(α)=(v1,⋯,vn)A x1⋮xn λα=λ(v1,⋯,vn) x1⋮xn
由于 v 1 , ⋯ , v n v_1,\cdots,v_n v1,⋯,vn线性无关,所以
A ( x 1 ⋮ x n ) = λ ( x 1 ⋮ x n ) A\begin{pmatrix}x_1\\\vdots\\x_n\end{pmatrix}=\lambda \begin{pmatrix}x_1\\\vdots\\x_n\end{pmatrix} A x1⋮xn =λ x1⋮xn
则说明特征向量 α \alpha α的坐标 x = ( x 1 ⋮ x n ) x=\begin{pmatrix}x_1\\\vdots\\x_n\end{pmatrix} x= x1⋮xn 满足齐次线性方程组 ( λ I − A ) x = 0 (\lambda I-A)x=0 (λI−A)x=0。因为 α ≠ 0 \alpha\neq 0 α=0,则 x ≠ 0 x\neq 0 x=0,即齐次线性方程组 ( λ I − A ) x = 0 (\lambda I-A)x=0 (λI−A)x=0有非零解。有非零解的充要条件是它的系数矩阵它的系数矩阵行列式 ∣ λ I − A ∣ = 0 |\lambda I-A|=0 ∣λI−A∣=0。
-
相关定义
设 A A A是数域 F F F上的 n n n阶矩阵, λ \lambda λ是一个符号,也是未知的特征值,矩阵 λ I − A \lambda I-A λI−A称为 A A A的特征矩阵,其行列式 ∣ λ I − A ∣ |\lambda I-A| ∣λI−A∣称为 A A A的特征多项式。方程 ∣ λ I − A ∣ = 0 |\lambda I-A|=0 ∣λI−A∣=0称为 A A A的特征方程,它的根(即 λ \lambda λ的值)称为 A A A的特征根(或特征值)。以 A A A的特征值 λ \lambda λ代入 A x = λ x Ax=\lambda x Ax=λx中所得到的非零解 x x x称为 A A A对应于 λ \lambda λ的特征向量。
-
定理
设 A A A为 n × n n\times n n×n矩阵, λ \lambda λ是一个数值,以下命题等价:
- λ \lambda λ是 A A A的特征值
- ( λ I − A ) x = 0 (\lambda I-A)x=0 (λI−A)x=0有一个非平凡的解(即有非零向量的解)
- N ( λ I − A ) ≠ { 0 } N(\lambda I-A)\neq\{0\} N(λI−A)={0}
- λ I − A \lambda I-A λI−A矩阵是奇异矩阵
- det ( λ I − A ) = 0 \det(\lambda I-A)=0 det(λI−A)=0
-
特征多项式的系数
如果
p ( λ ) = det ( λ I − A ) = λ n + ∑ k = 1 n ( − 1 ) k c k λ n − k = λ n − c 1 λ n − 1 + ⋯ + ( − 1 ) n − 1 c n − 1 λ + ( − 1 ) n c n p(\lambda)=\det(\lambda I-A)=\lambda^n+\sum_{\\k=1}^n(-1)^kc_k\lambda^{n-k}\\=\lambda ^n-c_1\lambda^{n-1}+\cdots+(-1)^{n-1}c_{n-1}\lambda+(-1)^nc_n p(λ)=det(λI−A)=λn+k=1∑n(−1)kckλn−k=λn−c1λn−1+⋯+(−1)n−1cn−1λ+(−1)ncn
则 c k ( 1 ≤ k ≤ n ) c_k(1\leq k\leq n) ck(1≤k≤n)是所有 k k k阶主子式(选择 k k k行 k k k列形成的行列式)的和,特别的, c 1 = t r ( A ) , c n = det ( A ) c_1=tr(A),c_n=\det(A) c1=tr(A),cn=det(A)。 -
定理
-
设 A ∈ C n × n A\in C^{n\times n} A∈Cn×n,如果 A A A有特征值 λ 1 , ⋯ , λ n \lambda_1,\cdots,\lambda_n λ1,⋯,λn,则
t r ( A ) = ∑ i = 1 n λ i , det ( A ) = ∏ i = 1 n λ i tr(A)=\sum_{\\i=1}^n\lambda_i,\det(A)=\prod_{i=1}^n\lambda_i tr(A)=i=1∑nλi,det(A)=i=1∏nλi -
如果 A A A相似 B B B,则两个矩阵有相同的特征值和特征多项式。
-
设 A ∈ C m × n A\in C^{m\times n} A∈Cm×n,则 A H A A^HA AHA和 A A H AA^H AAH特征值都是非负实数,且它们都有相同的非零特征值和相同的重数,并且非零特征值(包含重数)的数量等于 r a n k ( A ) rank(A) rank(A)。
-
2 对角化
-
定义
设矩阵 A ∈ F n × n A\in F^{n\times n} A∈Fn×n,如果存在一个非奇异矩阵 P ∈ F n × n P\in F^{n\times n} P∈Fn×n和一个对角矩阵 D ∈ F n × n D\in F^{n\times n} D∈Fn×n,使得 P − 1 A P = D P^{-1}AP=D P−1AP=D,则称 A A A可被对角化。
-
定理
- A A A可以被对角化当且仅当 A A A有 n n n个线性无关的特征向量
- λ 1 , ⋯ , λ k \lambda_1,\cdots,\lambda_k λ1,⋯,λk是 A A A的不同的特征值,则对应的特征向量 x 1 , ⋯ , x k x_1,\cdots,x_k x1,⋯,xk它们是线性无关的
- 由以上两条定理即可推出如果 A A A有 n n n个不同的特征值,则 A A A可被对角化
- 不同特征值对应的特征向量的集合的并集是线性无关的。即取每个特征值的所有特征向量,无论这些向量属于哪个特征值,它们的并集都是线性无关的。
-
代数重数
设 A ∈ F n × n A\in F^{n\times n} A∈Fn×n,如果 det ( λ I − A ) = ( λ − λ i ) r 1 ⋯ ( λ − λ k ) r k \det(\lambda I-A)=(\lambda -\lambda_i)^{r_1}\cdots(\lambda-\lambda_k)^{r_k} det(λI−A)=(λ−λi)r1⋯(λ−λk)rk,其中 λ 1 , ⋯ , λ k \lambda_1,\cdots,\lambda_k λ1,⋯,λk是 A A A的特征值,它们是不同的。则特征值 λ i \lambda_i λi的代数重数是 r i r_i ri,即特征值 λ i \lambda_i λi出现的次数。
-
几何重数
与特征值 λ i \lambda_i λi对应的特征子空间是 N ( λ i I − A ) N(\lambda_i I-A) N(λiI−A),则特征值 λ i \lambda_i λi的几何重数为 dim ( N ( λ i I − A ) ) \dim(N(\lambda_i I-A)) dim(N(λiI−A))。
几何重数$\leq $代数重数
-
几何重数看可对角化
矩阵 A ∈ F n × n A\in F^{n\times n} A∈Fn×n可对角化当且仅当 A A A中不同特征值的几何重数和等于 n n n(即每个特征值的代数重数都要等于几何重数)
3 Schur定理和正规矩阵
-
酉(正交)相似定义
设 A ∈ C n × n ( R n × n ) A\in C^{n\times n}(R^{n\times n}) A∈Cn×n(Rn×n),如果存在一个酉(正交)矩阵 U U U使得 U H A U = B ( U H = U − 1 ) U^HAU=B\space\space\space(U^H=U^{-1}) UHAU=B (UH=U−1),则可称 A A A酉(正交)相似 B B B
-
Schur定理
∀ A ∈ C n × n \forall A\in C^{n\times n} ∀A∈Cn×n, A A A都与上三角矩阵相似,且存在酉矩阵 U U U和上三角矩阵 T T T使得 U H A U = U − 1 A U = T U^HAU=U^{-1}AU=T UHAU=U−1AU=T。
仅适用于复数域,实数域上不一定适用
-
正规矩阵定义
设 A ∈ C n × n A\in C^{n\times n} A∈Cn×n,如果 A A A满足 A H A = A A H A^HA=AA^H AHA=AAH,则称 A A A是正规矩阵。
Hermite矩阵,酉(正交)矩阵都是正规矩阵
-
谱定理
设 A ∈ C n × n A\in C^{n\times n} A∈Cn×n,如果 A A A是Hermite矩阵,则 A A A酉相似于一个实对角矩阵,换句话说,Hermite矩阵的特征值都是实数。
-
引理
设 A ∈ C n × n A\in C^{n\times n} A∈Cn×n, A A A是正规矩阵当且仅当 ∀ λ , x \forall \lambda,x ∀λ,x使得 ∣ ∣ A x − λ x ∣ ∣ = ∣ ∣ A H x − λ ˉ x ∣ ∣ ||Ax-\lambda x||=||A^Hx-\bar{\lambda}x|| ∣∣Ax−λx∣∣=∣∣AHx−λˉx∣∣。
-
同时对角化
设 A , B A,B A,B都是相同阶数的正规矩阵,则存在一个酉矩阵可以同时酉对角化 A , B A,B A,B当且仅当 A B = B A AB=BA AB=BA
4 Python求解
import numpy as np
from sympy import symbols, Matrix
import pprint# 定义符号变量
lambda_ = symbols('lambda')A = np.array([[0, 2, 1], [-2, 0, 3], [-1, -3, 0]])
A = Matrix(A)# 求特征矩阵
characteristic_matrix = A - lambda_ * np.eye(3)
pprint.pprint("关于 lambda 的特征矩阵:")
pprint.pprint(characteristic_matrix)# 计算特征多项式
characteristic_polynomial = A.charpoly(lambda_)
pprint.pprint("关于 lambda 的特征多项式:")
pprint.pprint(characteristic_polynomial)# 求特征值
eigenvalues = A.eigenvals()
# 打印特征值、其代数重数、特征向量和几何重数for k, v in eigenvalues.items():pprint.pprint("特征值 %s 的代数重数为 %s" % (k, v))pprint.pprint("特征值 %s 的几何重数为 %s" % (k, A.eigenvects()[list(eigenvalues.keys()).index(k)][1]))pprint.pprint("特征值 %s 的特征向量为 %s" % (k, A.eigenvects()[list(eigenvalues.keys()).index(k)][2]))# 判断A是否可对角化,如果可以,打印出对角化矩阵
if A.is_diagonalizable():pprint.pprint("A可对角化")pprint.pprint("对角化矩阵为:")pprint.pprint(A.diagonalize()[0])# 求A的行空间、列空间、零空间
pprint.pprint("A的行空间为:")
pprint.pprint(A.rowspace())
pprint.pprint("A的列空间为:")
pprint.pprint(A.columnspace())
pprint.pprint("A的零空间为:")
pprint.pprint(A.nullspace())
相关文章:

【矩阵论】Chapter 4—特征值和特征向量知识点总结复习
文章目录 1 特征值和特征向量2 对角化3 Schur定理和正规矩阵4 Python求解 1 特征值和特征向量 定义 设 σ \sigma σ为数域 F F F上线性空间 V V V上的一个线性变换,一个非零向量 v ∈ V v\in V v∈V,如果存在一个 λ ∈ F \lambda \in F λ∈F使得 σ (…...

Linux 进程地址空间
知识回顾 在 C 语言的学习过程中,我们知道内存是可以被划分为栈区,堆区,全局数据区,字符常量区,代码区的。他的空间排布可能是下面的样子: 其中,全局数据区,可以划分为已初始化全局…...

websocket vue操作
let websocket: WebSocket; /** websocket测试 */ function connectWebsocket() {if (typeof WebSocket "undefined") {console.log("您的浏览器不支持WebSocket");return;}// let ip window.location.hostname ":8080";let ip "10.192…...
腾讯云CentOS8 jenkins war安装jenkins步骤文档
腾讯云CentOS8 jenkins war安装jenkins步骤文档 一、安装jdk 1.1 上传jdk-11.0.20_linux-x64_bin.tar.gz 1.2 解压jdk安装包文件 tar -zxvf jdk*.tar.gz 1.3 在/usr/local 目录下创建java目录 cd /usr/local mkdir java 1.4 切到java目录,把jdk解压文件改名为jd…...

Linux: glibc: net/if.h vs linux/if.h
最近看到一段代码改动,用net/if.h替换了linux/if.h。仔细看了看这两个的区别: https://stackoverflow.com/questions/20082433/what-is-the-difference-between-linux-if-h-and-net-if-h 从网上搜了一下看到如下的一个编译错误,如果同时使用这两个if.h文件,需要将net/if.h…...
使用Android Studio导入Android源码:基于全志H713 AOSP,方便解决编译、编码问题
文章目录 一、 篇头二、 操作步骤2.1 编译AOSP AS工程文件2.2 将AOSP导入Android Studio2.3 切到Project试图2.4 等待index结束2.5 下载缺失的JDK 1.82.6 导入完成 三、 导入AS的好处3.1 本文案例演示源码编译错误AS对比同文件其余地方的调用AS错误提示依赖AS做错误修正 一、 篇…...

python random详解
文章目录 random简单示例1. 生成随机浮点数:2. 生成指定范围内的随机整数:3. 从序列中随机选择元素:4. 打乱序列顺序: 常用的方法及其解释和例子:1. random():该方法返回一个0到1之间的随机浮点数。例如&am…...
java-两个列表进行比较,判断那些是需要新增的、删除的、和更新的
文章目录 前言两个列表进行比较,判断那些是需要新增的、删除的、和更新的 前言 如果您觉得有用的话,记得给博主点个赞,评论,收藏一键三连啊,写作不易啊^ _ ^。 而且听说点赞的人每天的运气都不会太差,实…...
【WPF.NET开发】WPF中的对话框
目录 1、消息框 2、通用对话框 3、自定义对话框 实现对话框 4、打开对话框的 UI 元素 4.1 菜单项 4.2 按钮 5、返回结果 5.1 模式对话框 5.2 处理响应 5.3 非模式对话框 Windows Presentation Foundation (WPF) 为你提供了自行设计对话框的方法。 对话框是窗口&…...

NLP项目实战01之电影评论分类
介绍: 欢迎来到本篇文章!在这里,我们将探讨一个常见而重要的自然语言处理任务——文本分类。具体而言,我们将关注情感分析任务,即通过分析电影评论的情感来判断评论是正面的、负面的。 展示: 训练展示如下…...

一款可无限扩展的软件定时器开源框架项目代码
摘自链接 时间片轮询架构如何稳定高效实现,取代传统的标志位判断方式,更优雅更方便地管理程序的时间触发操作。 可以在STM32单片机上运行。...

GRE与顺丰圆通快递盒子
1. DNS污染 随想: 在输入一串网址后,会发生如下变化如果你在系统中配置了 Hosts 文件,那么电脑会先查询 Hosts 文件如果 Hosts 里面没有这个别名,就通过域名服务器查询域名服务器回应了,那么你的电脑就可以根据域名服…...
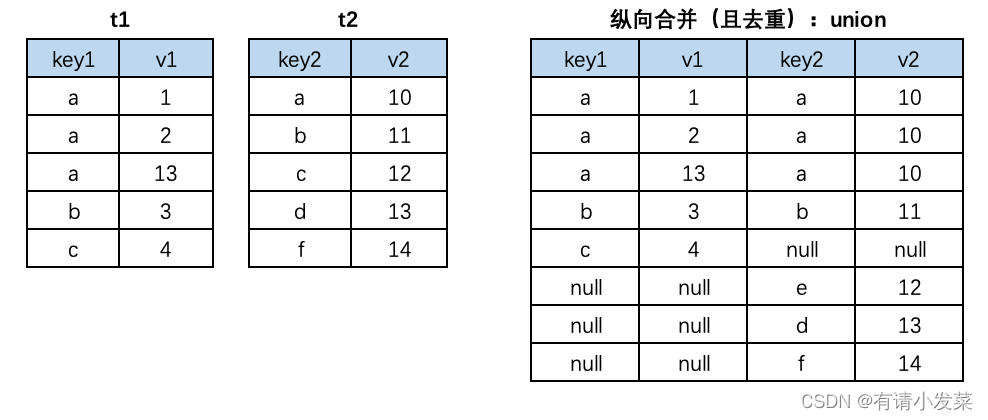
12.Mysql 多表数据横向合并和纵向合并
Mysql 函数参考和扩展:Mysql 常用函数和基础查询、 Mysql 官网 Mysql 语法执行顺序如下,一定要清楚!!!运算符相关,可前往 Mysql 基础语法和执行顺序扩展。 (8) select (9) distinct (11)<columns_name…...

线性回归与逻辑回归:深入解析机器学习的基石模型
目录 一、线性回归 二、逻辑回归 逻辑回归算法和 KNN 算法的区别 分类算法评价维度...

电脑待机怎么设置?让你的电脑更加节能
在日常使用电脑的过程中,合理设置待机模式是一项省电且环保的好习惯。然而,许多用户对于如何设置电脑待机感到困扰。那么电脑待机怎么设置呢?本文将深入探讨三种常用的电脑待机设置方法,通过详细的步骤,帮助用户更好地…...
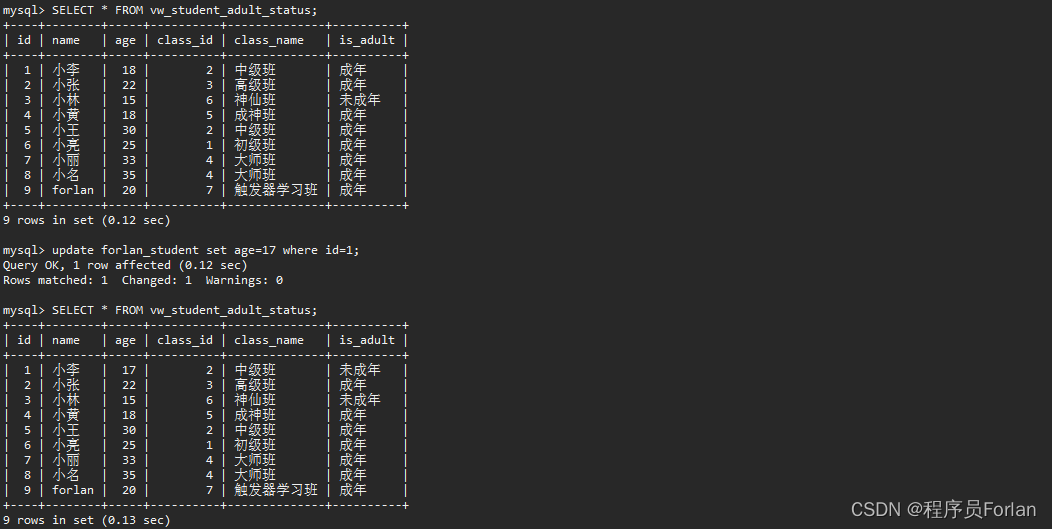
数据库对象介绍与实践:视图、函数、存储过程、触发器和物化视图
文章目录 一、视图(View)1、概念2、基本操作1)创建视图2)修改视图3)删除视图4)使用视图 3、使用场景4、实践 二、函数(Function)1、概念2、基本操作1)创建函数2ÿ…...

arm平台编译so文件回顾
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、几个点二、回顾过程 1.上来就执行Makefile2.编译第三方开源库.a文件 2.1 build.sh脚本2.2 Makefile3.最终编译三、其它知识点总结 前言 提示:这…...
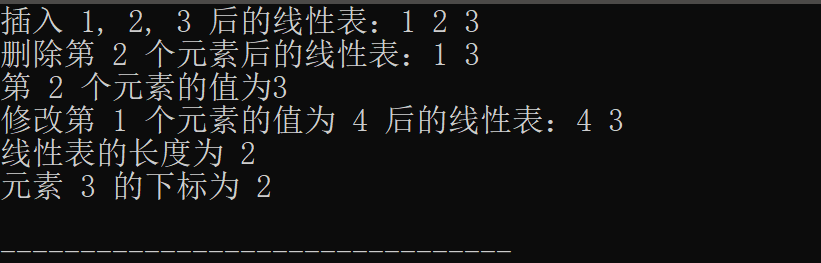
【数据结构】顺序表的定义和运算
目录 1.初始化 2.插入 3.删除 4.查找 5.修改 6.长度 7.遍历 8.完整代码 🌈嗨!我是Filotimo__🌈。很高兴与大家相识,希望我的博客能对你有所帮助。 💡本文由Filotimo__✍️原创,首发于CSDN📚。 &…...
idea使用maven的package打包时提示“找不到符号”或“找不到包”
介绍:由于我们的项目是多模块开发项目,在打包时有些模块内容更新导致其他模块在引用该模块时不能正确引入。 情况一:找不到符号 情况一:找不到包 错误代码部分展示: Failure to find com.xxx.xxxx:xxx:pom:0.5 in …...

MetricBeat监控MySQL
目录 一、安装部署 二、开启mysql监控模块 三、编辑mysql配置文件 四、启动Metricbeat 五、查看监控图表 一、安装部署 metriceat的安装部署参考章节: Metricbeat安装使用,这里不再赘述。 二、开启mysql监控模块 进入metricbeat安装目录 ./metricb…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...
