人工智能教程(三):更多有用的 Python 库

目录
前言
推荐
JupyterLab 入门
复杂的矩阵运算
其它人工智能和机器学习的 Python 库
前言
在本系列的上一篇人工智能教程(二):人工智能的历史以及再探矩阵中,我们回顾了人工智能的历史,然后详细地讨论了矩阵。在本系列的第三篇文章中,我们将了解更多的矩阵操作,同时再介绍几个人工智能 Python 库。
推荐
前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站
在进入主题之前,我们先讨论几个人工智能和机器学习中常用的重要术语。人工神经网络(artificial neural network)(通常简称为神经网络(neural network),NN)是机器学习和深度学习的核心。顾名思义,它是受人脑的生物神经网络启发而设计的计算模型。本文中我没有插入神经网络模型的图片,因为在互联网上很容易找到它们。我相信任何对人工智能感兴趣的人应该都见过它们,左边是输入层,中间是一个或多个隐藏层,右边是输出层。各层之间的边上的权重(weight) 会随着训练不断变化。它是机器学习和深度学习应用成功的关键。
监督学习(supervised learning) 和 无监督学习(unsupervised learning) 是两个重要的机器学习模型。从长远来看,任何立志于从事人工智能或机器学习领域工作的人都需要学习它们,并了解实现它们的各种技术。这里我认为有必要简单说明两种模型之间的区别了。假设有两个人分别叫 A 和 B,他们要把苹果和橘子分成两组。他们从未见过苹果或橘子。他们都通过 100 张苹果和橘子的图片来学习这两种水果的特征(这个过程称为模型的训练)。不过 A 还有照片中哪些是苹果哪些是橘子的额外信息(这个额外信息称为标签)。这里 A 就像是一个监督学习模型,B 就像是无监督学习模型。你认为在是识别苹果和橘子的任务上,谁的效果更好呢?大多数人可能会认为 A 的效果更好。但是根据机器学习的理论,情况并非总是如此。如果这 100 张照片中只有 5 张是苹果,其它都是橘子呢?那么 A 可能根本就不熟悉苹果的特征。或者如果部分标签是错误的呢?在这些情况下,B 的表现可能比 A 更好。
在实际的机器学习应用中会发生这样的情况吗?是的!训练模型用的数据集可能是不充分的或者不完整的。这是两种模型都仍然在人工智能和机器学习领域蓬勃发展的众多原因之一。在后续文章中,我们将更正式地讨论它们。下面我们开始学习使用 JupyterLab,它是一个用于开发人工智能程序的强大工具。
JupyterLab 入门
在本系列的前几篇文章中,为了简单起见,我们一直使用 Linux 终端运行 Python 代码。现在要介绍另一个强大的人工智能工具——JupyterLab。在本系列的第一篇文章中,我们对比了几个候选项,最终决定使用 JupyterLab。它比 Jupyter Notebook 功能更强大,为我们预装了许多库和包,并且易于团队协作。还有一些其它原因,我们将在后续适时探讨它们。
在本系列的第一篇文章中,我们已经学习了如何安装 JupyterLab。假设你已经按文中的步骤安装好了 JupyterLab,使用 jupyter lab 或 jupyter-lab 命令在会默认浏览器(如 Mozilla Firefox、谷歌 Chrome 等)中打开 JupyterLab。(LCTT 译注:没有安装 JupyterLab 也不要紧,你可以先 在线试用 JupyterLabjupyter.org)图 1 是在浏览器中打开的 JupyterLab 启动器的局部截图。JupyterLab 使用一个名为 IPython(交互式 Python)的 Python 控制台。注意,IPython 其实可以独立使用,在 Linux 终端运行 ipython 命令就可以启动它。

现阶段我们使用 JupyterLab 中的 Jupyter Notebook 功能。点击图 1 中用绿框标记的按钮,打开 Jupyter Notebook。这时可能会要求你选择内核。如果你按照本系列第一篇的步骤安装 JupyterLab,那么唯一的可选项就是 Python 3(ipykernel)。请注意,你还可以在 JupyterLab 中安装其它编程语言的内核,比如 C++、R、MATLAB、Julia 等。事实上 Jupyter 的内核相当丰富,你可以访问 Jupyter 内核清单github.com 了解更多信息。
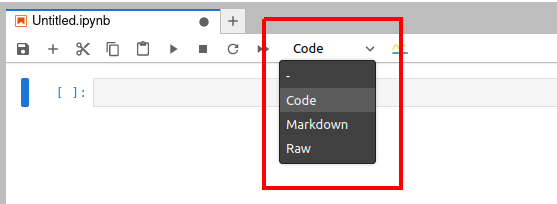
下面我们快速了解一下 Jupyter Notebook 的使用。图 2 显示的是一个在浏览器中打开的 Jupyter Notebook 窗口。从浏览器标签页的标题可以看出,Jupyter Notebook 打开的文件的扩展名是 .ipynb。
在图中可以看到有三个选项,它们表示 Jupyter Notebook 中可以使用的三种类型的单元。“Code”(绿色框) 表示代码单元,它是用来执行代码的。“Markdown” 单元可用于输入说明性的文本。如果你是一名计算机培训师,可以用代码单元和 Markdown 单元来创建交互式代码和解释性文本,然后分享给你的学员。“Raw”(红色框)表示原始数据单元,其中的内容不会被格式化或转换。
和在终端中不同,在 Jupyter Notebook 中你可以编辑并重新运行代码,这在处理简单的拼写错误时特别方便。图 3 是在 Jupyter Notebook 中执行 Python 代码的截图。
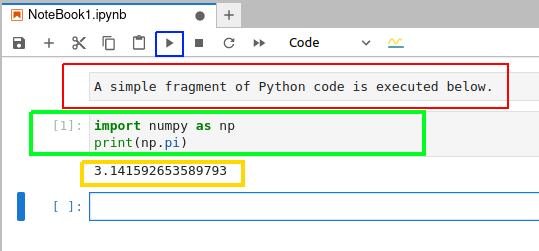
要在执行代码单元中的代码,先选中该单元格,然后点击蓝框标记的按钮。图示中用红框标记的是 Markdown 单元,用绿框标记的是代码单元,用黄框标记的执行代码的输出。在这个例子中,Python 代码输出的是 π 的值。
前面提到,JupyterLab 默认安装了许多库和包,我们不用自己安装了。你可以使用 import 命令将这些库导入到代码中。使用 !pip freeze 命令可以列出 JupyterLab 中目前可用的所有库和包。如果有库或包没有安装,大多数情况下都可以通过 pip install <全小写的库或者包的名称> 来安装它们。例如安装 TensorFlow 的命令是 pip install tensorflow。如果后面有库的安装命令不遵循这个格式,我会进行特别说明。随着本系列的继续,我们还会看到 Jupyter Notebook 和 JupyterLab 更多强大的功能。
复杂的矩阵运算
通过下面的代码,我们来了解一些更复杂的矩阵运算或操作。为了节省空间,我没有展示代码的输出。
import numpy as np
A = np.arr ay([[1,2,3],[4,5,6],[7,8,88]])
B = np.arr ay([[1,2,3],[4,5,6],[4,5,6]])
print(A.T)
print(A.T.T)
print(np.trace(A))
print(np.linalg.det(A))
C = np.linalg.inv(A)
print(C)
print(A@C)下面我逐行来解释这些代码:
- 导入 NumPy 包。
- 创建矩阵
A。 - 创建矩阵
B。 - 打印矩阵
A的转置(transpose)。通过比较矩阵A与A的转置,你用该可以大致理解转置操作到底做了什么。 - 打印
A的转置的转置。可以看到它和矩阵A是相同的。这又提示了转置操作的含义。 - 打印矩阵
A的 迹(trace)。迹是矩阵的对角线(也称为主对角线)元素的和。矩阵A的主对角线元素是 1、5 和 88,所以输出的值是 94。 - 打印
A的行列式(determinant)。当执行代码的结果是 -237.00000000000009(在你的电脑中可能略有区别)。因为行列式不为 0,所以称 A 为非奇异矩阵(non-singular matrix)。 - 将矩阵
A的逆(inverse) 保存到矩阵C中。 - 打印矩阵
C。 - 打印矩阵
A和C的乘积。仔细观察,你会看到乘积是一个单位矩阵(identity matrix),也就是一个所有对角线元素都为 1,所有其它元素都为 0 的矩阵。请注意,输出中打印出的不是精确的 1 和 0。在我得到的答案中,有像 -3.81639165e-17 这样的数字。这是浮点数的科学记数法,表示 -3.81639165 × 10-17, 即小数的 -0.0000000000000000381639165,它非常接近于零。同样输出中的其它数字也会有这种情况。我强烈建议你了解计算机是怎样表示浮点数的,这对你会有很大帮助。
根据第一篇文章中的惯例,可以将代码分成基本 Python 代码和人工智能代码。在这个例子中,除了第 1 行和第 9 行之外的所有代码行都可以被看作是人工智能代码。
现在将第 4 行到第 10 行的操作应用到矩阵 B 上。从第 4 行到第 6 行代码的输出没有什么特别之处。然而运行第 7 行时,矩阵 B 的行列式为 0,因此它被称为奇异矩阵(singular matrix)。运行第 8 行代码会给产生一个错误,因为只有非奇异矩阵才存在逆矩阵。你可以尝试对本系列前一篇文章中的 8 个矩阵都应用相同的操作。通过观察输出,你会发现矩阵的行列式和求逆运算只适用于方阵。
方阵就是行数和列数相等的矩阵。在上面的例子中我只是展示了对矩阵执行各种操作,并没有解释它们背后的理论。如果你不知道或忘记了矩阵的转置、逆、行列式等知识的话,你最好自己学习它们。同时你也应该了解一下不同类型的矩阵,比如单位矩阵、对角矩阵、三角矩阵、对称矩阵、斜对称矩阵。维基百科上的相关文章是不错的入门。
现在让我们来学习矩阵分解(matrix decomposition),它是更复杂的矩阵操作。矩阵分解与整数的因子分解类似,就是把一个矩阵被写成其它矩阵的乘积。下面我通过图 4 中整数分解的例子来解释矩阵分解的必要性。代码单元开头的 %time 是 Jupyter Notebook 的魔法命令(magic command),它会打印代码运行所花费的时间。** 是 Python 的幂运算符。基本的代数知识告诉我们,变量 a 和 b 的值都等于 (6869 x 7873)100。但图 4 显示计算变量 b 的速度要快得多。事实上,随着底数和指数的增大,执行时间的减少会越来越明显。
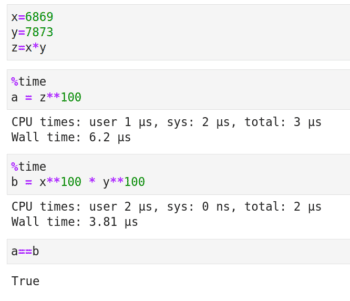
在几乎所有的矩阵分解技术技术中,原始矩阵都会被写成更稀疏的矩阵的乘积。稀疏矩阵(sparse matrix)是指有很多元素值为零的矩阵。在分解后,我们可以处理稀疏矩阵,而不是原始的具有大量非零元素的密集矩阵(dense matrix)。在本文中将介绍三种矩阵分解技术——LUP 分解、特征分解(eigen decomposition)和奇异值分解(singular value decomposition)(SVD)。
为了执行矩阵分解,我们需要另一个强大的 Python 库,SciPy。SciPy 是基于 NumPy 库的科学计算库,它提供了线性代数、积分、微分、优化等方面的函数。首先,让我们讨论 LUP 分解。任何方阵都能进行 LUP 分解。LUP 分解有一种变体,称为 LU 分解。但并不是所有方阵都能 LU 分解。因此这里我们只讨论 LUP 分解。
在 LUP 分解中,矩阵 A 被写成三个矩阵 L、U 和 P 的乘积。其中 L 是一个下三角矩阵(lower triangular matrix),它是主对角线以上的所有元素都为零的方阵。U 是一个上三角矩阵(upper triangular matrix),它是主对角线以下所有元素为零的方阵。P 是一个排列矩阵(permutation matrix)。这是一个方阵,它的每一行和每一列中都有一个元素为 1,其它元素的值都是 0。
现在看下面的 LUP 分解的代码。
import numpy as np
import scipy as sp
A=np.array([[11,22,33],[44,55,66],[77,88,888]])
P, L, U = sp.linalg.lu(A)
print(P)
print(L)
print(U)
print(P@L@U)图 5 显示了代码的输出。第 1 行和第 2 行导入 NumPy 和 SciPy 包。在第 3 行创建矩阵 A。请记住,我们在本节中会一直使用矩阵 A。第 4 行将矩阵 A 分解为三个矩阵——P、L 和 U。第 5 行到第 7 行打印矩阵 P、L 和 U。从图 5 中可以清楚地看出,P 是一个置换矩阵,L 是一个下三角矩阵,U 是一个上三角矩阵。最后在第 8 行将这三个矩阵相乘并打印乘积矩阵。从图 5 可以看到乘积矩阵 P@L@U 等于原始矩阵 A,满足矩阵分解的性质。此外,图 5 也验证了矩阵 L、U 和 P 比矩阵 A 更稀疏。

下面我们讨论特征分解,它是将一个方阵是用它的特征值(eigenvalue)和特征向量(eigenvector)来表示。用 Python 计算特征值和特征向量很容易。关于特征值和特征向量的理论解释超出了本文的讨论范围,如果你不知道它们是什么,我建议你通过维基百科等先了解它们,以便对正在执行的操作有一个清晰的概念。图 6 中是特征分解的代码。
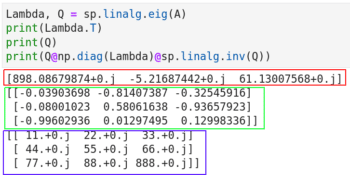
在图 6 中,第 1 行计算特征值和特征向量。第 2 行和第 3 行输出它们。注意,使用 NumPy 也能获得类似的效果,Lambda, Q = np.linalg.eig(A)。这也告诉我们 NumPy 和 SciPy 的功能之间有一些重叠。第 4 行重建了原始矩阵 A。第 4 行中的代码片段 np.diag(Lambda) 是将特征值转换为对角矩阵(记为 Λ)。对角矩阵是主对角线以外的所有元素都为 0 的矩阵。第 4 行的代码片段 sp.linalg.inv(Q) 是求 Q 的逆矩阵(记为 Q-1)。最后,将三个矩阵 Q、Λ、Q-1 相乘得到原始矩阵 A。也就是在特征分解中 A=QΛQ-1。
图 6 还显示了执行的代码的输出。红框标记的是特征值,用绿框标记的是特征向量,重构的矩阵 A 用蓝框标记。你可能会感到奇怪,输出中像 11.+0.j 这样的数字是什么呢?其中的 j 是虚数单位。11.+0.j 其实就是 11.0+0.0j,即整数 11 的复数形式。
现在让我们来看奇异值分解(SVD),它是特征分解的推广。图 7 显示了 SVD 的代码和输出。第 1 行将矩阵 A 分解为三个矩阵 U、S 和 V。第 2 行中的代码片段 np.diag(S) 将 S 转换为对角矩阵。最后,将这三个矩阵相乘重建原始矩阵 A。奇异值分解的优点是它可以对角化非方阵。但非方阵的奇异值分解的代码稍微复杂一些,我们暂时不在这里讨论它。

其它人工智能和机器学习的 Python 库
当谈到人工智能时,普通人最先想到的场景可能就是电影《终结者》里机器人通过视觉识别一个人。计算机视觉(computer vision)是人工智能和机器学习技术被应用得最广泛的领域之一。下面我将介绍两个计算机视觉相关的库:OpenCV 和 Matplotlib。OpenCV 是一个主要用于实时计算机视觉的库,它由 C 和 C++ 开发。C++ 是 OpenCV 的主要接口,它通过 OpenCV-Python 向用户提供 Python 接口。Matplotlib 是基于 Python 的绘图库。我曾在 OSFY 上的一篇早期 文章www.opensourceforu.com 中详细介绍了 Matplotlib 的使用。
前面我一直在强调矩阵的重要性,现在我用一个实际的例子来加以说明。图 8 展示了在 Jupyter Notebook 中使用 Matplotlib 读取和显示图像的代码和输出。如果你没有安装 Matplotlib,使用 pip install matplotlib 命令安装 Matplotlib。
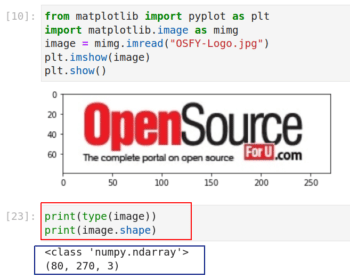
图 8:用 Matplotlib 读取和显示图像
在图 8 中,第 1 行和第 2 行从 Matplotlib 导入了一些函数。注意你可以从库中导入单个函数或包,而不用导入整个库。这两行是基本的 Python 代码。第 3 行从我的计算机中读取标题为 OSFY-Logo.jpg 的图像。我从 OSFY 门户网站的首页下载了这张图片。此图像高 80 像素,宽 270 像素。第 4 行和第 5 行在 Jupyter Notebook 窗口中显示图像。请注意图像下方用红框标记的两行代码,它的输出告诉我们变量 image 实际上是一个 NumPy 数组。具体来说,它是一个 80 x 270 x 3 的三维数组。
数组尺寸中的 80 x 270 就是图片的大小,这一点很容易理解。但是第三维度表示什么呢?这是因计算机像通常用 RGB 颜色模型来存储的彩色图。它有三层,分别用于表示红绿蓝三种原色。我相信你还记得学生时代的实验,把原色混合成不同的颜色。例如,红色和绿色混合在一起会得到黄色。在 RGB 模型中,每种颜色的亮度用 0 到 255 的数字表示。0 表示最暗,255 表示最亮。因此值为 (255,255,255) 的像素表示纯白色。
现在,执行代码 print(image), Jupyter Notebook 会将整个数组的一部分部分打印出来。你可以看到数组的开头有许多 255。这是什么原因呢?如果你仔细看 OSFY 的图标会发现,图标的边缘有很多白色区域,因此一开始就印了很多 255。顺便说一句,你还可以了解一下其他颜色模型,如 CMY、CMYK、HSV 等。
现在我们反过来从一个数组创建一幅图像。首先看图 9 中所示的代码。它展示了如何生成两个 3 x 3 的随机矩阵,它的元素是 0 到 255 之间的随机值。注意,虽然相同的代码执行了两次,但生成的结果是不同的。这是通过调用 NumPy 的伪随机数生成器函数 randint 实现的。实际上,我中彩票的几率都比这两个矩阵完全相等的几率大得多。

接下来我们要生成一个形状为 512 x 512 x 3 的三维数组,然后将它转换为图像。为此我们将用到 OpenCV。注意,安装 OpenCV 命令是 pip install opencv-python。看下面的代码:
import cv2
img = np.random.randint(0, 256, size=(512, 512, 3))
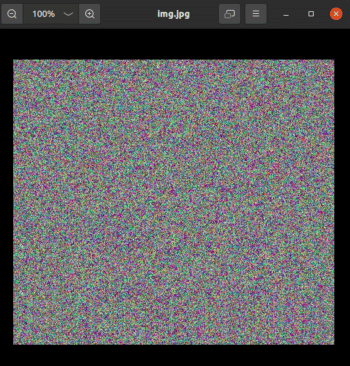
cv2.imwrite('img.jpg', img)第 1 行导入库 OpenCV。注意导入语句是 import cv2,这与大多数其他包的导入不同。第 3 行将矩阵 img 转换为名为 img.jpg 的图像。图 10 显示了由 OpenCV 生成的图像。在系统中运行这段代码,将图像将被保存在 Jupyter Notebook 的同一目录下。如果你查看这张图片的属性,你会看到它的高度是 512 像素,宽度是 512 像素。通过这些例子,很容易看出,任何处理计算机视觉任务的人工智能和机器学习程序使用了大量的数组、向量、矩阵以及线性代数中的思想。这也是本系列用大量篇幅介绍数组、向量和矩阵的原因。
最后,考虑下面显示的代码。image.jpg 输出图像会是什么样子?我给你两个提示。函数 zeros 在第 4 行和第 5 行创建了两个 512 x 512 的数组,其中绿色和蓝色填充了零。第 7 行到第 9 行用来自数组 red、green 和 blue 的值填充三维数组 img1。
import numpy as np
import cv2
red = np.random.randint(0, 256, size=(512, 512))
green = np.zeros([512, 512], dtype=np.uint8)
blue = np.zeros([512, 512], dtype=np.uint8)
img1 = np.zeros([512,512,3], dtype=np.uint8)
img1[:,:,0] = blue
img1[:,:,1] = green
img1[:,:,2] = red
cv2.imwrite(‘image.jpg’, img1)本期的内容就到此结束了。在下一篇文章中,我们将开始简单地学习张量(tensor),然后安装和使用 TensorFlow。TensorFlow 是人工智能和机器学习领域的重要参与者。之后,我们将暂时放下矩阵、向量和线性代数,开始学习概率论。概率论跟线性代数一样是人工智能的重要基石。
相关文章:

人工智能教程(三):更多有用的 Python 库
目录 前言 推荐 JupyterLab 入门 复杂的矩阵运算 其它人工智能和机器学习的 Python 库 前言 在本系列的上一篇人工智能教程(二):人工智能的历史以及再探矩阵中,我们回顾了人工智能的历史,然后详细地讨论了矩阵。在…...

【带头学C++】----- 九、类和对象 ---- 9.10 C++设计模式之单例模式设计
❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️麻烦您点个关注,不迷路❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️ 目 录 9.10 C设计模式之单例模式设计 举例说明: 9.10 C设计模式之单例模式设计 看过我之前的文章的,简单讲解过C/Q…...

Qt之QCache和QContiguousCache
一.QCache QCache在构造的时候指定了缓存中允许的最大成本,也就是如下构造函数中的参数maxCost。默认情况下,QCaches maxCost() 是100。 QCache(int maxCost = 100) ~QCache() void clear() bool contains(const Key &key) const int count() const bool insert(const …...
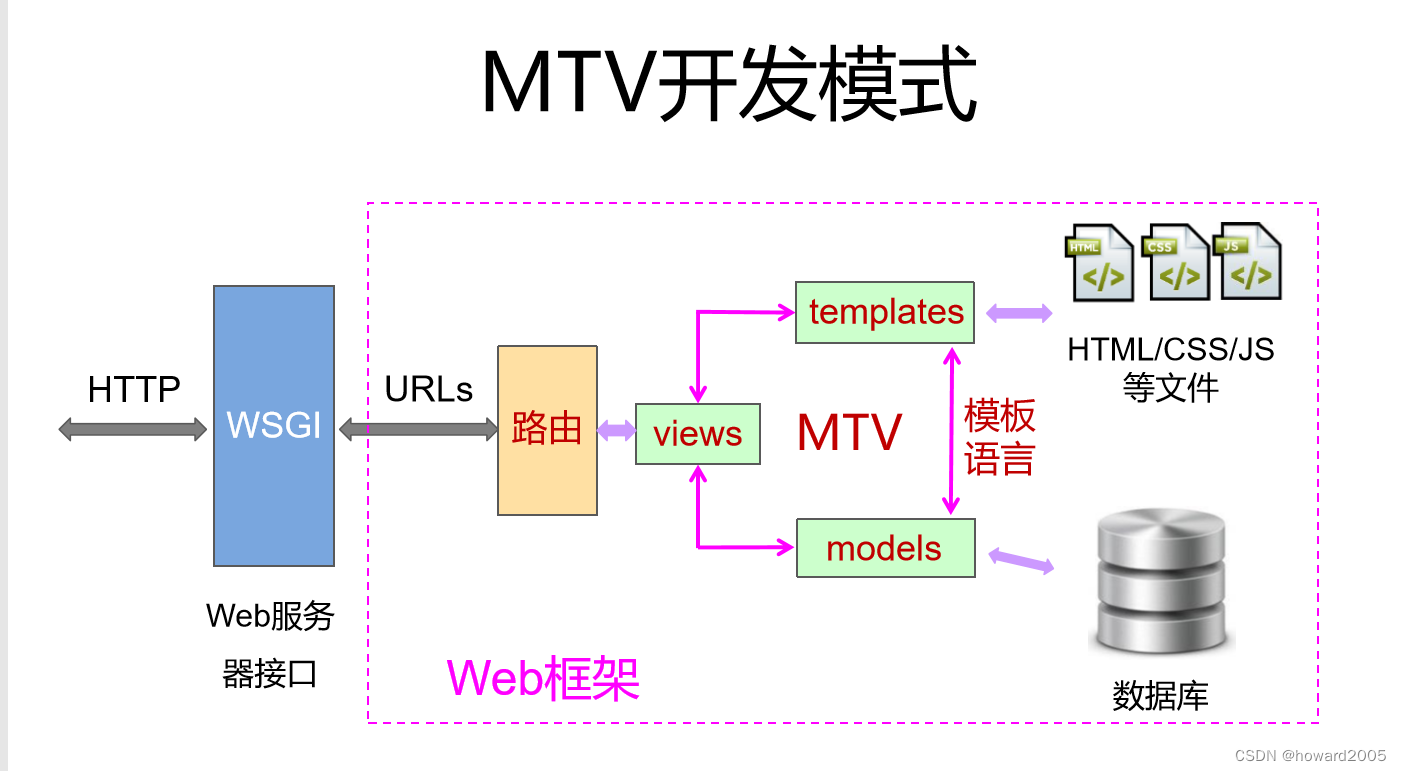
Django讲课笔记01:初探Django框架
文章目录 一、学习目标二、课程导入(一)课程简介(二)课程目标(三)适用人群(四)教学方式(五)评估方式(六)参考教材 三、新课讲授&#…...

JS中的闭包
闭包 闭包的概念其实很简单,就是函数A内部有一个函数B,函数B可以访问函数A的变量。也就是说闭包是指有权访问另一个函数作用域中变量的函数,利用闭包可以突破作用域链。 闭包的特性: 1、函数内再嵌套函数 2、内部函数可以引用外层的参数和变…...
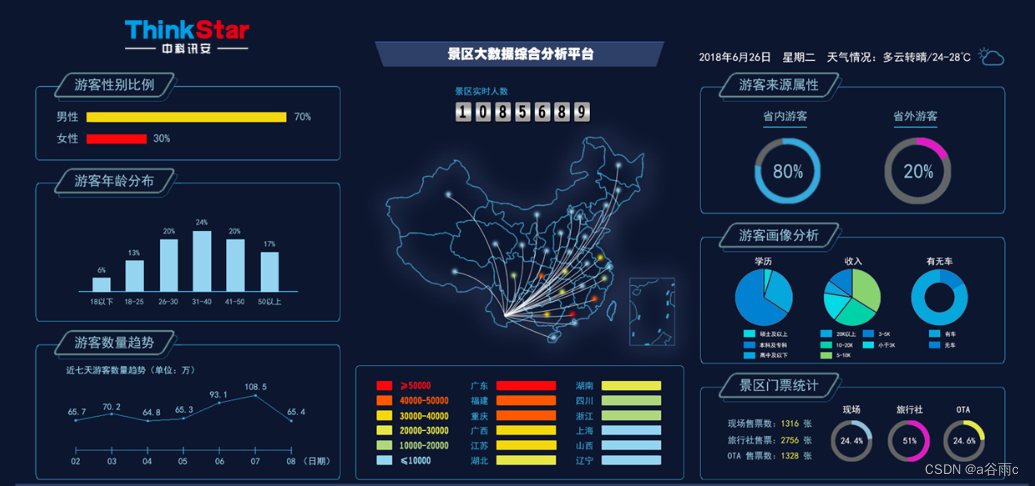
深度学习在计算机视觉中的应用
深度学习在计算机视觉中的应用 摘要:本文介绍了深度学习在计算机视觉领域的应用,包括目标检测、图像分类、人脸识别等。通过分析深度学习在计算机视觉中的实际应用案例,阐述了深度学习在计算机视觉中的优势和未来发展趋势。 一、引言 计算…...

模板与泛型编程
函数模板 显示实例化 区别定义与声明 T是模板形参 int是模板实参 inpunt是函数形参 3是函数实参 显示实例化 模板必须实例化可见 翻译单元一处定义原则 与内联函数异同 引入原因:函数模板是为了编译器两个阶段的处理 内联函数是为了能在编译期展开 模板实参的类…...
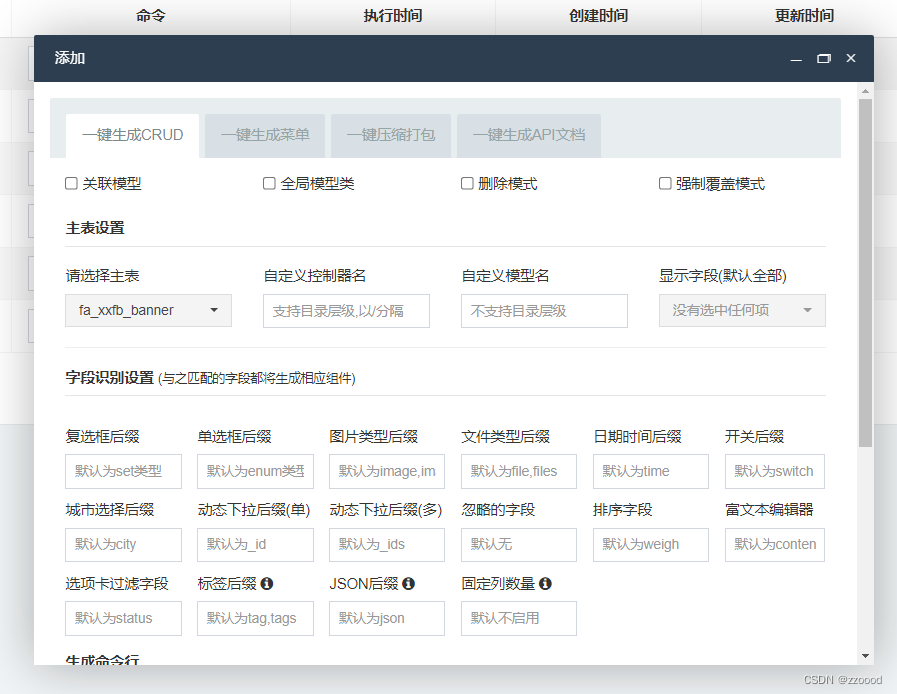
【Fastadmin】一个完整的轮播图功能示例
目录 1.效果展示: 列表 添加及编辑页面同 2.建表: 3.使用crud一键生成并创建控制器 4.html页面 add.html edit.html index.php 5.js页面 6.小知识点 1.效果展示: 列表 添加及编辑页面同 2.建表: 表名:fa_x…...

Ribbon 饥饿加载
Ribbon默认是采用懒加载,即第一次访问时才会去创建LoadBalanceClient,请求时间会很长而饥饿加载则会在项目启动时创建,降低第一次访问的耗时,通过下面配置开启饥饿加载: 一、懒加载 Ribbon 默认为懒加载即在首次启动Application…...
【AIGC】大语言模型的采样策略--temperature、top-k、top-p等
总结如下: 图片链接 参考 LLM解码-采样策略串讲 LLM大模型解码生成方式总结 LLM探索:GPT类模型的几个常用参数 Top-k, Top-p, Temperature...

pip的基本命令和使用
Pip的基本命令和使用 介绍 Pip是Python的包管理工具,它能够帮助我们安装、升级和卸载Python模块。它是Python标准库的一部分,因此在大多数Python发行版中都已经预装了Pip。本文将介绍Pip的基本命令和使用方法,帮助读者更好地使用Pip管理Pyt…...
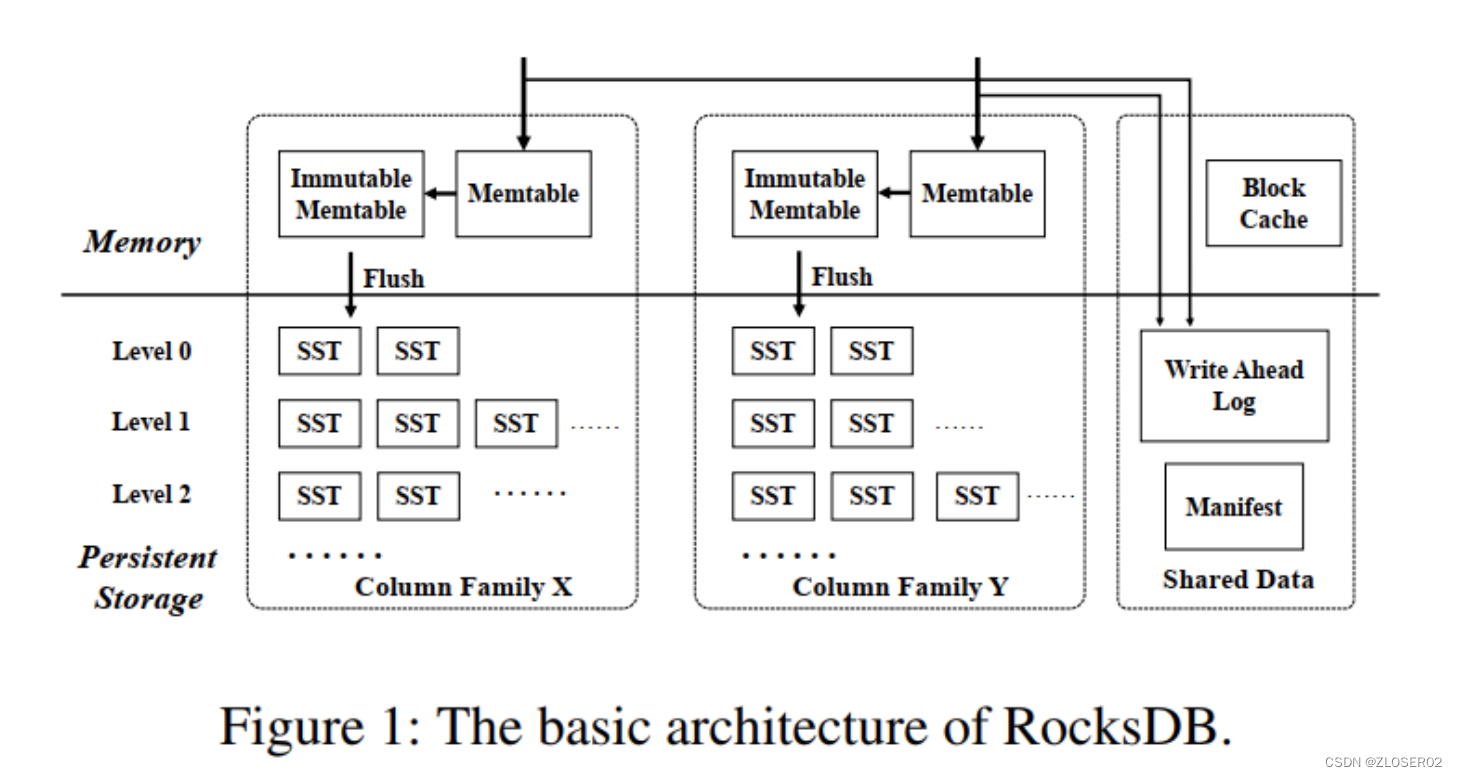
RocksDB实现原理
文章目录 简介编译安装RocksDB压缩库UbuntuCentos 基本接口高度分层架构LSM-Tree关于访问速度 MemTable落盘策略 WALRocksDB 中的每个更新操作都会写到两个地方:WAL 创建时机:重要参数 Immutable MemTableSSTBlockCacheLRU 缓存Clock缓存 写入流程读取流…...

mysql 链接超时的几个参数详解
mysql5.7版本中,先查看超时设置参数,我们这里只关注需要的超时参数,并不是全都讲解 show variables like %timeout%; connect_timeout 指的是连接过程中握手的超时时间,在5.0.52以后默认为10秒,之前版本默认是5秒,主…...
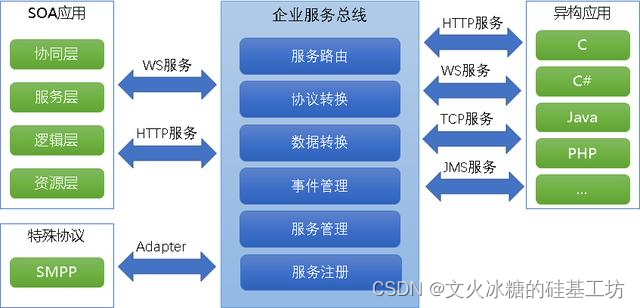
[架构之路-259]:目标系统 - 设计方法 - 软件工程 - 软件设计 - 架构设计 - 面向服务的架构SOA与微服务架构(以服务为最小的构建单位)
目录 前言: 二、软件架构层面的复用 三、什么是面向服务的架构SOA 3.1 什么是面向服务的架构 3.2 面向服务架构的案例 3.3 云服务:everything is service一切皆服务 四、什么是微服务架构 4.1 什么是微服务架构 4.2 微服务架构的案例 五、企业…...
7z压缩成jar包
比如我们要改下jar包中的某个文件,或者更换一下,那么就要先解压。解压后是这样的 弄好后,使用7z进行压缩,7z默认是标准压缩,会把BOOT-INF\lib 目录下的jar包也进行一次压缩,这会导致java -jar 会报 jar包相…...

python-缩进式编码+算术运算符+定义与赋值代码示例
文章目录 一、缩进式编码二、算术运算符三、定义与赋值关于Python技术储备一、Python所有方向的学习路线二、Python基础学习视频三、精品Python学习书籍四、Python工具包项目源码合集①Python工具包②Python实战案例③Python小游戏源码五、面试资料六、Python兼职渠道 一、…...

APM性能分享观看有感
应用性能监控是什么 应用 ios,app,pc 性能 performance用户体验,注重快:流畅,稳:崩溃,省:资源占用省 监控那些性能 一,快: 1.启动监控:冷启…...

免费好用的API接口攻略
台风信息查询:提供西北太平洋及南海地区过去两年及当前年份所有编号台风的信息查询,包括台风实时位置、过去路径、预报路径及登陆信息等要素。短信验证码:可用于登录、注册、找回密码、支付认证等等应用场景。支持三大运营商,3秒可…...

五、C#笔记
/// <summary> /// 第八章:理解值和引用 /// </summary> namespace Chapter8 { class Program { static void Main(string[] args) { //8.1复制值类型的变量和类 int i 42; int copyi i…...
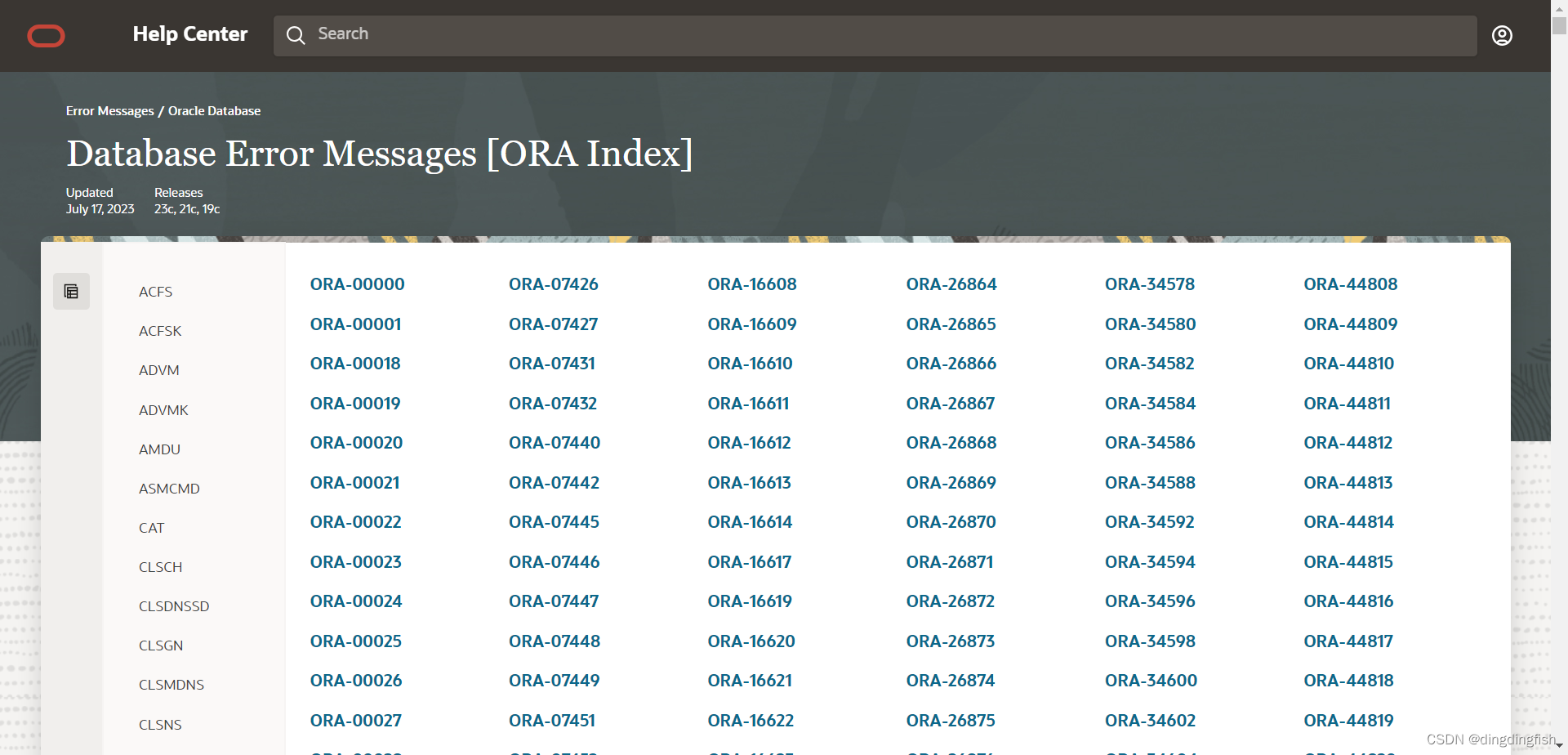
Oracle的错误信息帮助:Error Help
今天看手册时,发现上面有个提示: Error messages are now available in Error Help. 点击 View Error Help,显示如下,其实就是oerr命令的图形化版本: 点击Database Error Message Index,以下界面等同于命令…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...
实现跳一跳小游戏)
鸿蒙(HarmonyOS5)实现跳一跳小游戏
下面我将介绍如何使用鸿蒙的ArkUI框架,实现一个简单的跳一跳小游戏。 1. 项目结构 src/main/ets/ ├── MainAbility │ ├── pages │ │ ├── Index.ets // 主页面 │ │ └── GamePage.ets // 游戏页面 │ └── model │ …...
