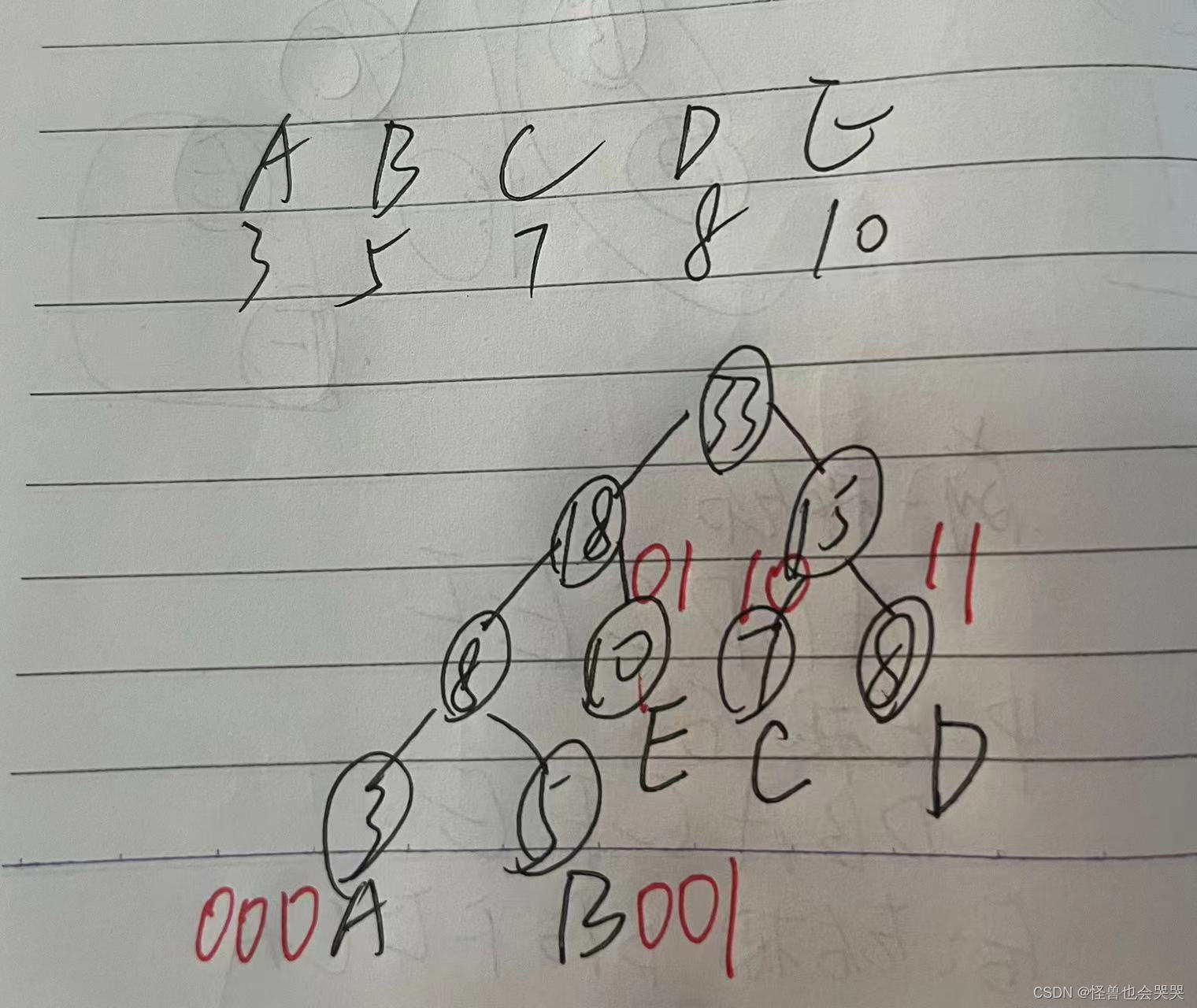数据结构第二次作业——递归、树、图【考点罗列//错题正解//题目解析】
目录
一、选择题
——递归——
1.【单选题】 ——递归的相关知识点
2.【单选题】——递归的应用
3.【单选题】——递归的实现结构
4.【单选题】——递归的执行与实现
5.【单选题】 ——递归算法
——树——
6.【单选题】 ——树的结构
*7.【单选题】——树的知识点
8.【单选题】——求二叉树的结点
*9.【单选题】 ——求二叉树的双分支结点
10.【单选题】 ——求二叉树指定结点的双亲结点编号与右孩子编号
11.【单选题】——二叉树的遍历算法
12.【单选题】 ——二叉树的后序遍历序列
13.【单选题】——二叉树的前中后序序列 判断
14.【单选题】——求二叉树的中序遍历序列
15.【单选题】 ——二叉树的后序遍历序列
16.【单选题】——线索二叉树的相关知识点
17.【单选题】——求二叉树的指向指针域数目
18.【单选题】——哈夫曼树的相关知识点
19.【单选题】——求哈夫曼树的单分支节点数目
20.【单选题】——求字符的哈夫曼编码长度
——图——
21.【单选题】——图的相关知识点
22.【单选题】——图的遍历
23.【单选题】——生成树的相关知识点
24.【单选题】——图:最短路径
25.【单选题】 ——图:拓扑排序
二、填空题
——递归——
26.【填空题】——递归的概念
27.【填空题】——求递归调用次数
28.【填空题】 ——递归模型
29.【填空题】——求递归调用次数
30.【填空题】——递归算法:代码填写
——树——
31.【填空题】——树:求叶子结点的度
32.【填空题】——二叉树:求最少结点
*33.【填空题】——求二叉树结点总数
34.【填空题】 ——求完全树的结点总数
35.【填空题】——树:指定结点的左孩子结点判断
36.【填空题】 ——树:递归结构的构成部分
37.【填空题】——树:中序遍历序列
编辑
*38.【填空题】——树:结点判读
39.【填空题】——二叉树:后序遍历算法
40.【填空题】 ——二叉树的深度
41.【填空题】——二叉树:链式存储结构的指针域数目求解
42.【填空题】 ——二叉树:指定结点的右孩子结点
43.【填空题】——哈夫曼树:求带权路径长度
44.【填空题】——哈夫曼树:结点数目
*45.【填空题】 ——字符的哈夫曼编码
——图——
46.【填空题】——图的相关知识点
47.【填空题】——图:邻接表存储结构的构成部分
48.【填空题】——图:遍历方法
49.【填空题】——生成树的边数求解
50.【填空题】——最小生成树的算法
一、选择题
——递归——
1.【单选题】 ——递归的相关知识点
以下关于递归的说法中,哪一项是不正确的?(D )
A.数据结构中部分地包含其自身,则此数据结构是递归的。
B.函数内部调用其自身,则此函数是递归的。
C.递归调用语句出现在递归函数中的最后一句,则此递归调用称为尾递归。
D.如果函数中没有出现对其自身的调用语句,则该函数一定不是递归的函数。
选项D:如果函数p调用函数q,而q又调用p,即便函数 p没有出现对自身的调用,但是函数p在调用函数q的过程中间接调用了自己本身,这称之为间接递归。
2.【单选题】——递归的应用
以下哪一项应用问题与递归无关?(D )。
A.求正整数n的阶乘
B.查找单链表最后一个结点
C.求解汉诺塔问题
D.打印机任务调度
选项D:个人理解的话,因为打印机的任务调度是”先进先出“,也就是队列的问题,而递归程序的实现是基于数据结构:栈上的,所以排除D。其余三个选项都是递归的相关应用
3.【单选题】——递归的实现结构
递归程序的实现需要使用以下哪一种数据结构?( C)。
A.顺序表
B.链表
C.栈
D.队列
栈的一个重要应用是:在程序设计语言中实现递归算法
4.【单选题】——递归的执行与实现
以下关于递归的执行与实现的说法中,哪一项是不正确的?( C)。
A.递归的执行是一个把“大问题”分解为“小问题”,再反向求解的过程。
B.为避免递归程序无限执行,在满足特定条件时,将不再进行递归调用。
C.每一次递归调用时,都会在存储空间单独放置一份递归调用的程序代码。
D.当发生一次递归调用时,在递归工作栈执行的是“入栈”操作。
选项A:在这里涉及到“递归模型”。一个递归出口,一个递归体。递归算法实际上就是将一个复杂问题的描述与求解过程变得简洁明了,也就是“大问题”化“小问题”,再反向求解。具体可看29题的一个推导过程
- 递归体表示“大问题”与“小问题”的关系。
- 递归出口为“最小问题”,分解到最小问题的时候,再将其重新带回递归体,最终就是“最大问题”的结果。
选项B:从递归模型就可知,当满足特定的终止条件时,递归算法也就随之结束了。
选项C:递归调用的程序代码只有一份,每次调用的操作数、局部变量等都会分配新的空间。
选项D:这里涉及到递归工作栈。在递归的层层分解过程中,也就是每发生一次递归调用,“这一次”的参数以及对应的函数返回地址就会进行入栈操作,直到遇到“递归出口”的 条件,栈达到最顶层,对应存放元素是递归出口条件对应的返回值。这样在将大问题拆分为小问题后,才能再“原路返回”,求得最终的值。因此每一次的递归调用就相当于一次“入栈”,以便下一层返回值时重新使用它们。
5.【单选题】 ——递归算法
以下关于递归算法与非递归算法的说法中,哪一项是不正确的?( C)。
A.递归算法可转换为非递归算法。
B.尾递归算法可转换为使用循环语句实现的算法。
C.递归算法的时间效率比使用循环语句实现的算法高。
D.递归算法的空间效率比使用循环语句实现的算法低。
选项A:求解问题的过程中,当然可以先使用递归算法分析问题,然后通过将递归算法转化为非递归算法,再进行问题的求解
选项B:这里补充《转换方法》
直接转化:尾递归,可用循环结构的算法替代。
间接转化:
- 需要使用栈:自己用栈模拟系统的运行时栈,通过分析只保存必须保存的信息。
- 需要使用系统栈:利用系统栈保存参数。由于系统不了解程序的业务逻辑,仅从技术上转换,有可能保存不必要的信息。
选项C:不一定。递归算法的基本特性中讲到,递归算法本身时间效率通常比较差。求解某些问题时,先用递归算法分析问题,再用非递归算法具体求解问题。需要把递归算法转换为非递归算法。
选项D:这是因为递归算法在执行过程中需要不断地将函数的参数、局部变量和返回地址等信息保存在递归工作栈中,而每次递归调用都会占用额外的内存空间。与此相比,使用循环语句实现的算法则不需要保存函数调用的相关数据,它只需要保存循环控制变量和一些局部变量,因此在空间上更加高效。
——树——
6.【单选题】 ——树的结构
以下哪一项应用问题与树的结构无关?( C)。
A.HTML代码解析
B.公司组织结构安排
C.两个有序表合并
D.文件系统中文件夹与文件的存储
【这道题就针对选项A和C进行解释】
选项A:HTML代码解析通常涉及标签的嵌套和结构,这与树的结构有关。在HTML中,标签的嵌套关系可以用树的结构来表示,因此与树的结构有关。
选项C:在合并两个有序表的过程中,我们只需要比较两个表中的元素大小,并按照顺序将它们合并成一个新的有序表。这个过程并不需要使用树的结构或者树相关的算法。
*7.【单选题】——树的知识点
以下关于树和二叉树的说法中,正确的是?(A )。C
A.树中同一层次的结点互为兄弟结点。
B.二叉树是度为2的有序树。
C.满二叉树一定是完全二叉树。
D.已知二叉树的结点总数,可求得其深度。
【在做题的时候,这道题尤其考虑了很久,感觉模棱两可的选项,但是一对答案反倒是想了起来,当时排除C是被自己绕了进去,从“一定是”纠结到“充要”的关系,最后反推完全二叉树不一定就能推出是满二叉树,因此排除(被自己整笑了😀)】
选项A:具有相同父结点的节点才是兄弟结点。而在树中,同一层次的节点只是具有相同的祖先节点而已。
选项B:缺少了完整的定义,不一定是度为2的二叉树,二叉树结点的度取值在[0、1、2],至多有两颗子树,也可以没有子树
选项C:
满二叉树 每一层上的结点数都是最大结点数,即每一层i的结点数都具有最大值(2的i-1次方),也就是说所有的分支结点都具有左右子树。 完全二叉树 是指除了最后一层外,其他层都是满的,并且最后一层的节点都尽量靠左排列。 所以 满二叉树是一种特殊的完全二叉树 选项D:该二叉树是完全二叉树才可使用相应公式: log2(结点总数 )+ 1来求树的深度
8.【单选题】——求二叉树的结点
已知一颗深度为10的满二叉树,则其第10层的结点数和整颗树的结点数分别为:(D )。
A.1024,2048
B.255,512
C.1023,2047
D.512,1023
求解公式:
非空二叉树的第 i (i≥1)层上最多有
个结点
深度为 h (h≥1)的非空二叉树最多有
个结点。
所以第10层上最多有 个结点,也就是512个
所以整棵树最多有 ,也就是1024-1,1023个
*9.【单选题】 ——求二叉树的双分支结点
已知一颗完全二叉树的结点总数为1000,则这颗完全二叉树的双分支结点数为( C)。B
A.498
B.499
C.500
D.501
((结点总数n)/2)-1
10.【单选题】 ——求二叉树指定结点的双亲结点编号与右孩子编号
按从上至下,从左至右的顺序对一颗完全二叉树的所有结点进行编号(树根的编号为1)。设编号为451的结点为A结点,其有右孩子结点,则A结点的右孩子结点的编号,以及A结点的父结点的编号分别为:(D )。
A.901,224
B.900,224
C.902,226
D.903,225
【二叉树的性质】n个结点的完全二叉树,按从上至下,从左至右的次序对结点编号,则编号为 i 的结点有以下性质:
- 若编号为 i 的结点有左孩子,则左孩子的编号为 2i
- 若编号为 i 的结点有右孩子,则右孩子的编号为 2i+1
- 除树根结点外,若一个结点的编号为 i,则它的双亲结点的编号为 [ i/2 ]
已知结点A编号为451,所以其右孩子的结点是2*451+1=903,父结点为451/2=225
11.【单选题】——二叉树的遍历算法
以下关于二叉树遍历的说法中,哪一项是正确的?(D )。
A.对二叉树进行中序遍历,是先访问其右子树结点,再访问根,最后访问左子树结点。
B.已知二叉树的前序遍历序列和后序遍历序列,可确定这颗二叉树的形态。
C.已知二叉树的带空树位置的中序遍历序列,可确定这颗二叉树的形态。
D.一颗二叉树的后序遍历序列一定是唯一的。
选项A:中序遍历(左子树 ->根->右子树)
选项B:只有知道中序和后序,或中序和前序遍历序列才能唯一确定一颗二叉树
选项C:任意一个遍历序列均不能唯一确定一颗二叉树
选项D:毋庸置疑
12.【单选题】 ——二叉树的后序遍历序列
一颗二叉树的根结点为A,则以下哪一项可能为二叉树的后序遍历序列?( B)。
A.AGECDBF
B.GCDEBFA
C.ABCDEFG
D.DECAFBG
秒杀题:
前序遍历(根 ->左子树 ->右子树)
后序遍历(左子树 ->右子树->根)
所以在本题中,知道了根节点是A,那么后序遍历的最后一个结点必然是A
13.【单选题】——二叉树的前中后序序列 判断
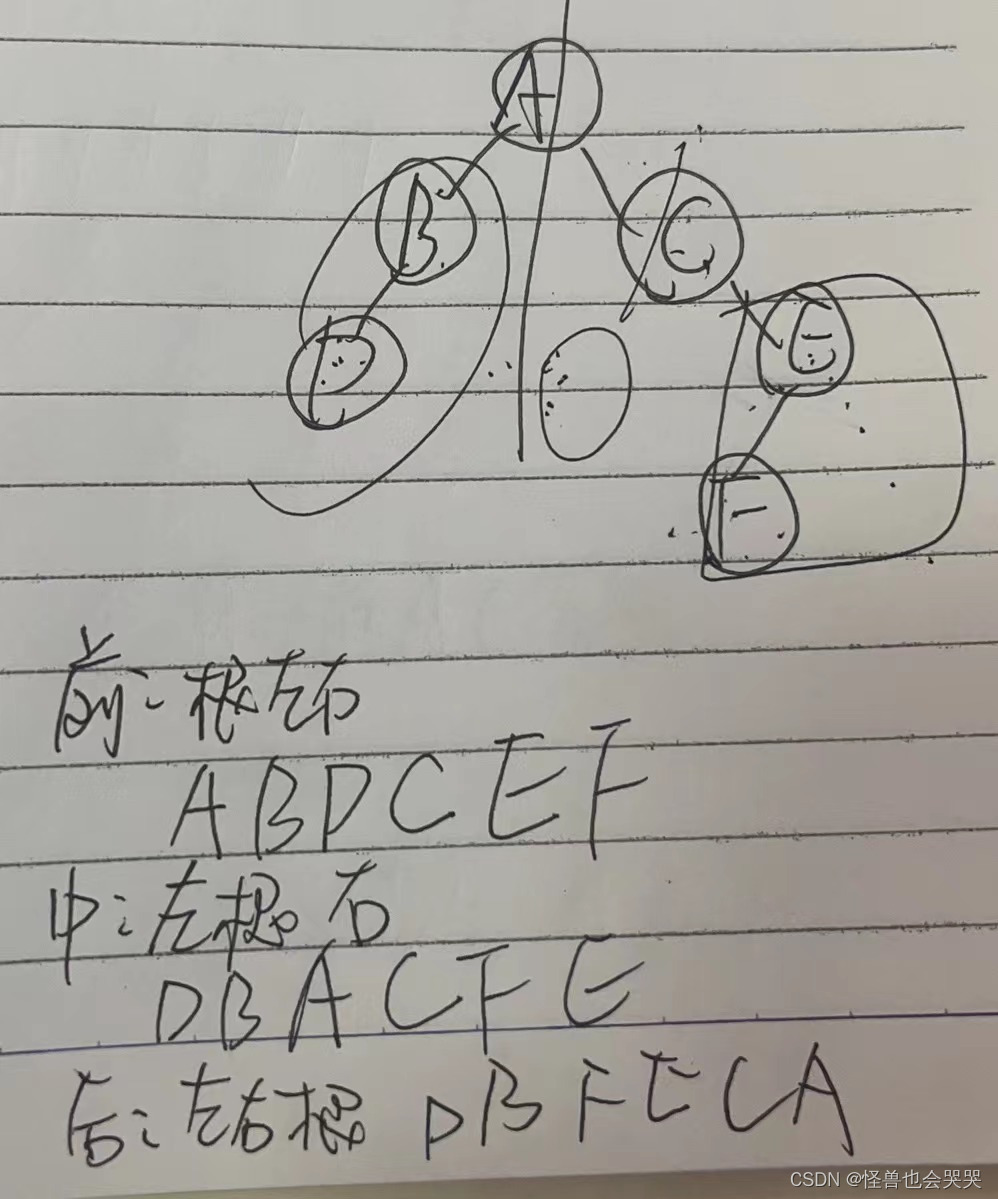
二叉树如下图所示,则以下哪一项不属于二叉树的前序、或中序、或后序遍历序列?( D)。
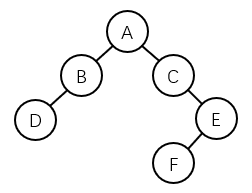
A.DBFECA
B.DBACFE
C.ABDCEF
D.DBACEF
解题过程如下:排除三个,只有选项D不在这三个序列结果中。
14.【单选题】——求二叉树的中序遍历序列
已知二叉树的中序遍历序列为EDBFCA,后序遍历序列为EFBDAC,则这颗二叉树的前序遍历序列为( C)。
A.ACDBEF
B.EBCDAF
C.CDEBFA
D.FBEADC
秒杀题:
知道后序遍历序列——最后一个结点为根结点——C
这道题刚刚好问的是前序遍历序列,也就是第一个结点为根节点,刚刚好选项ABCD中只有选项C的第一个结点是结点C,秒杀。
15.【单选题】 ——二叉树的后序遍历序列
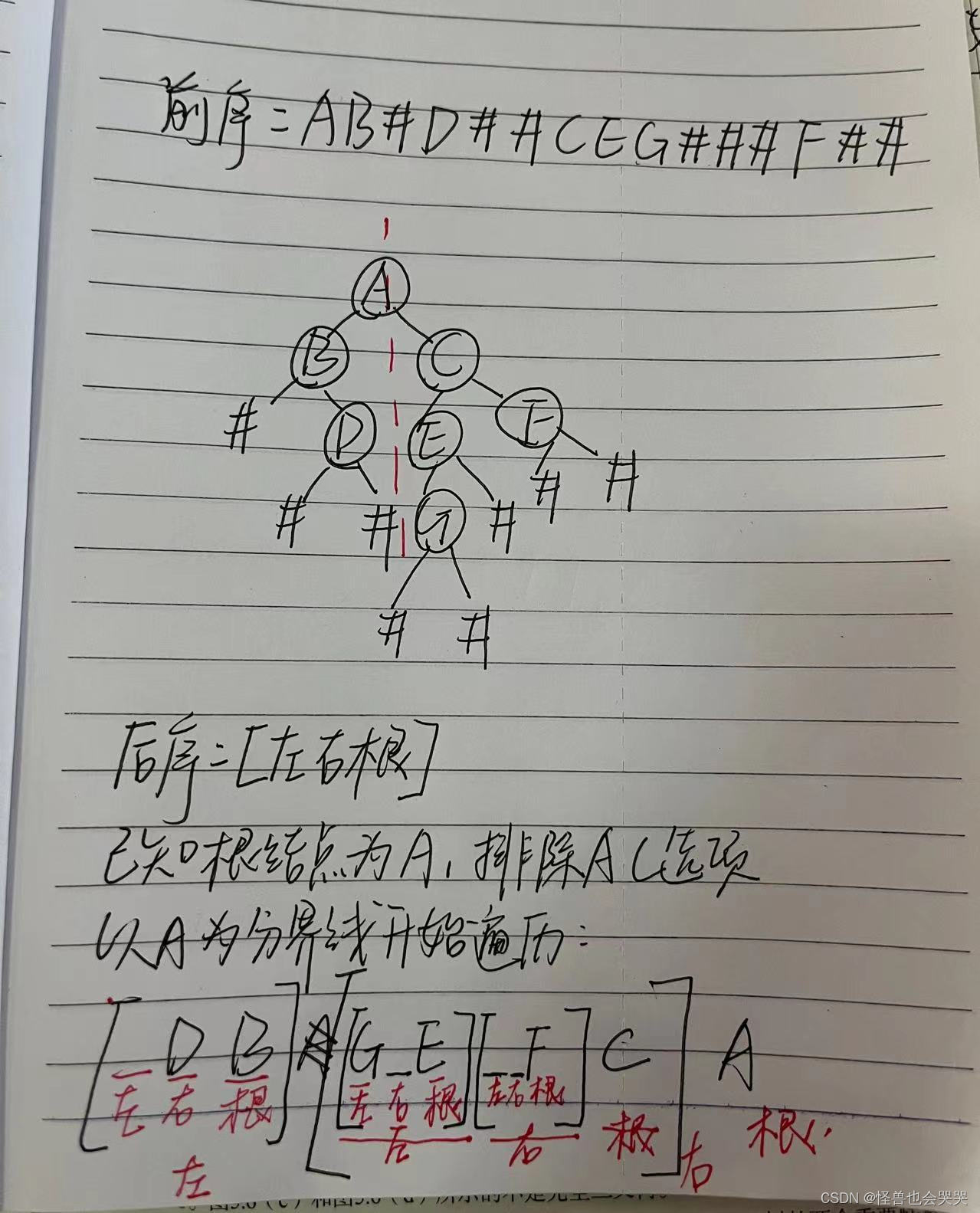
已知二叉树的带空树(#)位置的前序遍历序列为AB#D##CEG###F##,则这颗二叉树的后序遍历序列为( D)。
A.BCAGDEF
B.GEFCDBA
C.BDACEGF
D.DBGEFCA
解题过程如下:
16.【单选题】——线索二叉树的相关知识点
以下关于线索二叉树的说法中,哪一项是不正确的?(C )。
A如果结点的左指针为空,则将其设置为指向该结点的前驱结点的线索
B.如需判断结点的右指针是否为线索,则需判断结点中右标志域的取值。
C.创建线索二叉树时不需要进行递归遍历,从而节省了时间。
创建线索二叉树时,需要进行中序遍历来对二叉树中的每个结点进行线索化处理,这是一个递归过程。虽然线索化后的遍历操作可以更高效地进行,但是创建线索二叉树时依然需要进行递归遍历。
D.线索二叉树是结合二叉链表与单链表的特性而设计的存储结构
17.【单选题】——求二叉树的指向指针域数目
一颗二叉树有n个结点,则其链式存储结构中,指向孩子结点的指针域的数目为( C)。
A.2n
B.n
C.n-1
D.n+1
因为在二叉树的链式存储结构中:
每个结点最多只有两个孩子结点,因此指向孩子结点的指针域的数目为每个结点的2个孩子结点的指针域之和,即2n;
但是由于根结点没有父结点,因此孩子结点的指针数目比结点数目少1,所以指向孩子结点的指针域的数目为n-1。
18.【单选题】——哈夫曼树的相关知识点
以下关于哈夫曼树的说法中,哪一项是正确的?(D )。
A.带权路径长度最大的二叉树称为哈夫曼树。
B.给定权值建立的哈夫曼树,只能有一种形态。
C.在哈夫曼树中,权值越大的叶子结点越远离根结点。
D.哈夫曼树可以用于设计哈夫曼编码。
选项A:最短
选项B:多种形态
选项C:
- 应该是权值越小的越远离根节点
- 权值越大的应该更靠近根节点
选项D:yes,根据给出的权值结点画出二叉树后,一般规定左边为0右边为1,以此一层层添加二进制数
19.【单选题】——求哈夫曼树的单分支节点数目
哈夫曼树中的单分支结点数目是(B )。
A.与叶子结点数目相同。
B.0。
C.与双分支结点数目相同。
D.叶子结点数目减1。
这道题要联想到哈夫曼树的构造过程算法,答案就出来了。
20.【单选题】——求字符的哈夫曼编码长度
题20. 设在电文中包含的字符有: A,B,C,D,E,各字符出现的次数依次为: 3,5,7,8,10。 设计哈夫曼编码以表示各字符,则字符B的哈夫曼编码的长度为(C )个二进制位。
A.1
B.2
C.3
D.4
求解过程如下:
——图——
21.【单选题】——图的相关知识点
以下关于图的说法中,哪一项是正确的?(D )。
A.连通图是指图中任意两个顶点之间均有边直接相连。
B.有向图的邻接矩阵沿对角线对称。
C.当图的顶点数目较多,边的数目较少时,选择邻接矩阵作为存储结构较为合适。
D.邻接表的设计既包含顺序存储结构,也包含链式存储结构。
选项A:将直接删去,因为只要该图任意两点间有路径【边】即可描述为连通图
选项B:
无向图的邻接矩阵沿对角线对称。
有向图的邻接矩阵不一定对称。
选项C:因为当图的顶点数目较多,边的数目较少时,选择邻接表作为存储结构更为合适。
邻接矩阵 是一个二维数组,其大小为|V| * |V|,其中|V|是图的顶点数目。因此,当图的顶点数目较多时,邻接矩阵会占用大量的空间,即使边的数目较少,也会浪费大量的空间。 相比之下 邻接表 是由一个数组和一组链表(或其他动态数据结构)组成的,对于边的存储只需要占用与边数成正比的空间。因此,当图的顶点数目较多,边的数目较少时,选择邻接表作为存储结构更为合适,可以节省大量的空间。 选项D:邻接表——由顶点表和边表组成,是顺序与链式存储结构的结合
22.【单选题】——图的遍历
以下关于图的遍历的说法中,哪一项是不正确的?( D)。
A.图的遍历可选择任意顶点作为起点。
B.图的深度优先遍历是一个递归的过程。
C.图的广度优先遍历需借助队列结构实现。
D.图的深度优先遍历序列是唯一的。
选项A:yes,起点可以任选图中的一点
选项B:yes,深度优先遍历(DFS)算法过程如下:
(1)从图的某一顶点v出发(起点任选),访问此顶点; (2)选择一个与顶点v相邻且未被访问过的顶点w,再从w出发进行深度优先遍历(递归),直至图中所有和v连通的顶点都被访问过为止; (3)若此时图中尚有顶点未被访问,则另选图中一个未被访问的顶点作起点,重复上述过程,直至图中所有顶点都被访问为止。 选项C:yes,借助队列结构可以实现图的广度优先遍历
选项D:结合A选项一起看,因为图的遍历是可以任意选择起点的,所以无论是深度遍历还是广度遍历,有多少个顶点就可以有多少种选择起点的方法,因此得出来的结果是不唯一的
23.【单选题】——生成树的相关知识点
以下关于生成树的说法中,哪一项是不正确的?( C)。
A.连通图的生成树包含连通图的全部顶点。
B.有 n 个顶点的连通图,其生成树有 n-1 条边。
C.同一连通图,使用普里姆(Prim)算法和克鲁斯卡尔(Kruskal)算法构造的最小生成树是相同的。
D.最小生成树可用于解决以最小成本铺设连通管道的实际问题。
选项A:定义——连通图的生成树,包含连通图全部顶点的极小连通子图。即以最少的边连接连通图中所有的顶点。
选项B:性质——有n个顶点的连通图,它的生成树包含n个顶点和n-1条边。若加上一条边则构成环,若减去一条边则是非连通图。
选项C:虽然 Prim 算法和 Kruskal 算法都可以构造出连通图的最小生成树,但是对于同一张图,它们构造的最小生成树不一定相同。
选项D:yes,最小生成树的实际应用
24.【单选题】——图:最短路径
以下关于最短路径的说法中,哪一项是不正确的?( C)。
A.带权图中,从源点到终点的所有路径中,边的权值之和最小的路径称为最短路径。
B.狄克斯特拉(Dijkstra)算法求解单源点最短路径,初始时已确定最短路径的顶点为源点。
C.狄克斯特拉(Dijkstra)算法求解单源点最短路径,按最短路径长度的递减次序依次求解。
D.带权图中,源点到终点的最短路径可能有多条。
选项A:定义——带权图中从源点到终点的所有路径中,所经过边的权值之和最小的路径称为最短路径。
选项B:单源点最短路径——从一个顶点到其余各顶点的最短路径。
选项C:应该是递增次序。按最短路径长度的递增次序依次把(U=V-S)组的顶点加入S中。加入时,总保持从源点到S中各顶点的最短路径长度小于等于从源点到U中各顶点的当前最短路径长度。
25.【单选题】 ——图:拓扑排序
在拓扑排序的算法中,每次输出的结点是( A)。
A.入度为0的结点
B.出度为0的结点
C.入度和出度均为0的结点
D.入度或出度为0的结点
拓扑排序的算法过程:
从有向图中选择一个没有前驱(即入度为0)的顶点并且输出它;
从网中删去该顶点,并且删去从该顶点发出的全部有向边;
重复上述两步,直到剩余的网中不再存在没有前驱的顶点为止。
二、填空题
——递归——
26.【填空题】——递归的概念
如果递归函数内出现对其自身的调用语句,则这种递归可称为 直接 递归。
27.【填空题】——求递归调用次数
在使用递归实现的求解汉诺塔问题的函数中,共有 2 (阿拉伯数字)条递归调用语句。
void Hanoi(int n, char X, char Y, char Z)
{ //n表示需要移动盘子的数量,X表示源塔,Y表示借用塔,Z表示目标塔if (n == 1) //只有一个盘子时,将其从X塔移动到Z塔cout << X << "->" << Z << "\t";else {//①借助Z塔,将前n-1个盘子从X塔移动到Y塔Hanoi(n - 1, X, Z, Y);//②将X塔上剩下的1个盘子移到Z塔cout << X << "->" << Z << "\t";//③借助X塔,将前n-1个盘子从Y塔移动到Z塔Hanoi(n - 1, Y, X, Z);}
}
28.【填空题】 ——递归模型
递归问题的模型包含递归出口和__递归体_两个部分。
29.【填空题】——求递归调用次数
如果使用递归算法求正整数的阶乘,则当求 10 的阶乘时,将发生_9__(阿拉伯数字)次递归调用。
解题过程如下:
30.【填空题】——递归算法:代码填写
设A为整数数组,从位置0到n-1放置n个整数。以下是求数组中n个整数之和的递归算法实现,程序划线处应填入的语句是:__n-1_ (答案不含空格)

——树——
31.【填空题】——树:求叶子结点的度
在树结构中,叶子结点的度为 __0_(阿拉伯数字) 。
32.【填空题】——二叉树:求最少结点
一颗深度为8的完全二叉树最少有 __128_(阿拉伯数字)个结点。
这道题容易做错,一不小心的话就会得到255的答案。
我们知道可以利用:深度为 h (h≥1)的非空二叉树最多有
个结点。这条性质去求已知深度的二叉树结点最高数目。但是这一题问的是最少数目
换个思路,也就是在满七层的基础上多1个结点,因此
就是深度为8的完全二叉树拥有的最少结点。
*33.【填空题】——求二叉树结点总数
已知一颗二叉树的单分支结点数为5,双分支结点数为8,则这颗二叉树的结点总数为 14。22
解题过程:
(1)一棵树的结点:双分支+单分支+叶子结点
(2)非空二叉树上的叶子结点数=双分支结点数+1
这道题给出单分支结点数是5,双分支结点数是8,
那么就可以知道叶子结点的数目是9
所以这棵树的结点总数=5+8+9=22
34.【填空题】 ——求完全树的结点总数
已知一颗完全二叉树的第7层有63个结点,则这颗完全树总共有__126_(阿拉伯数字)个结点。
解题过程:
这里要想到这两条性质:
- 非空二叉树的第 i (i≥1)层上最多有
个结点
- 深度为 h (h≥1)的非空二叉树最多有
个结点。
第7层最多有
个结点,也就是64个,题目说明了第七层有63个还差一个满,也就是前六层结点都是满的
所以前六层的结点最多有
个,也就是63个
那么满了的六层结点加上第七层的63个就是结点总数:63+63=126
35.【填空题】——树:指定结点的左孩子结点判断
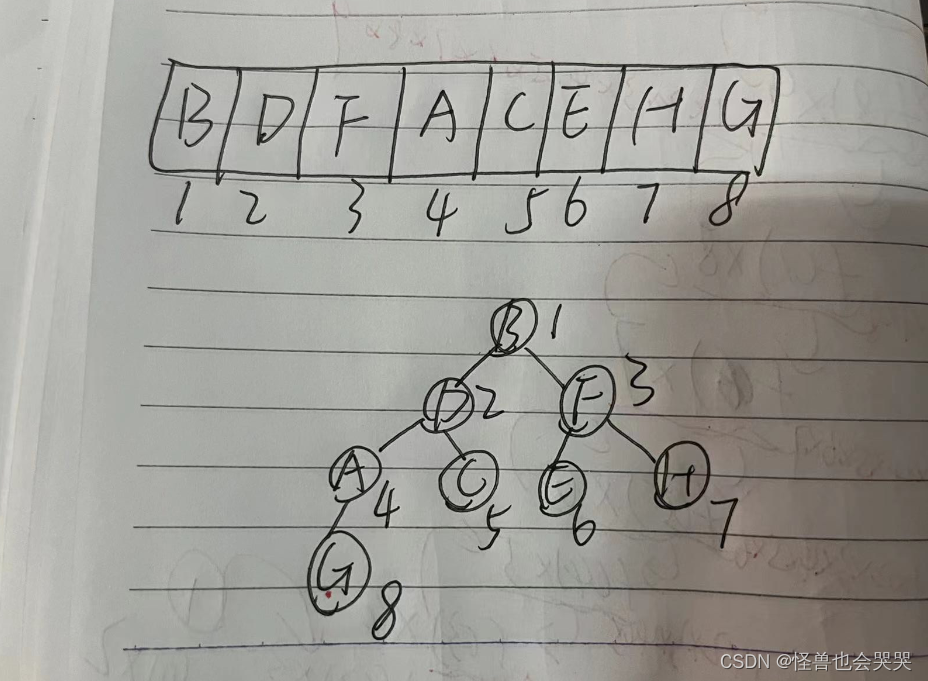
以下是一颗完全二叉树的顺序存储结构,则F结点的左孩子结点是 _E__ 结点。

解题过程如下:
36.【填空题】 ——树:递归结构的构成部分
如果将二叉树看作是递归的数据结构,则可以将二叉树分解为 _根__ 结点 、左子树和右子树三个部分。
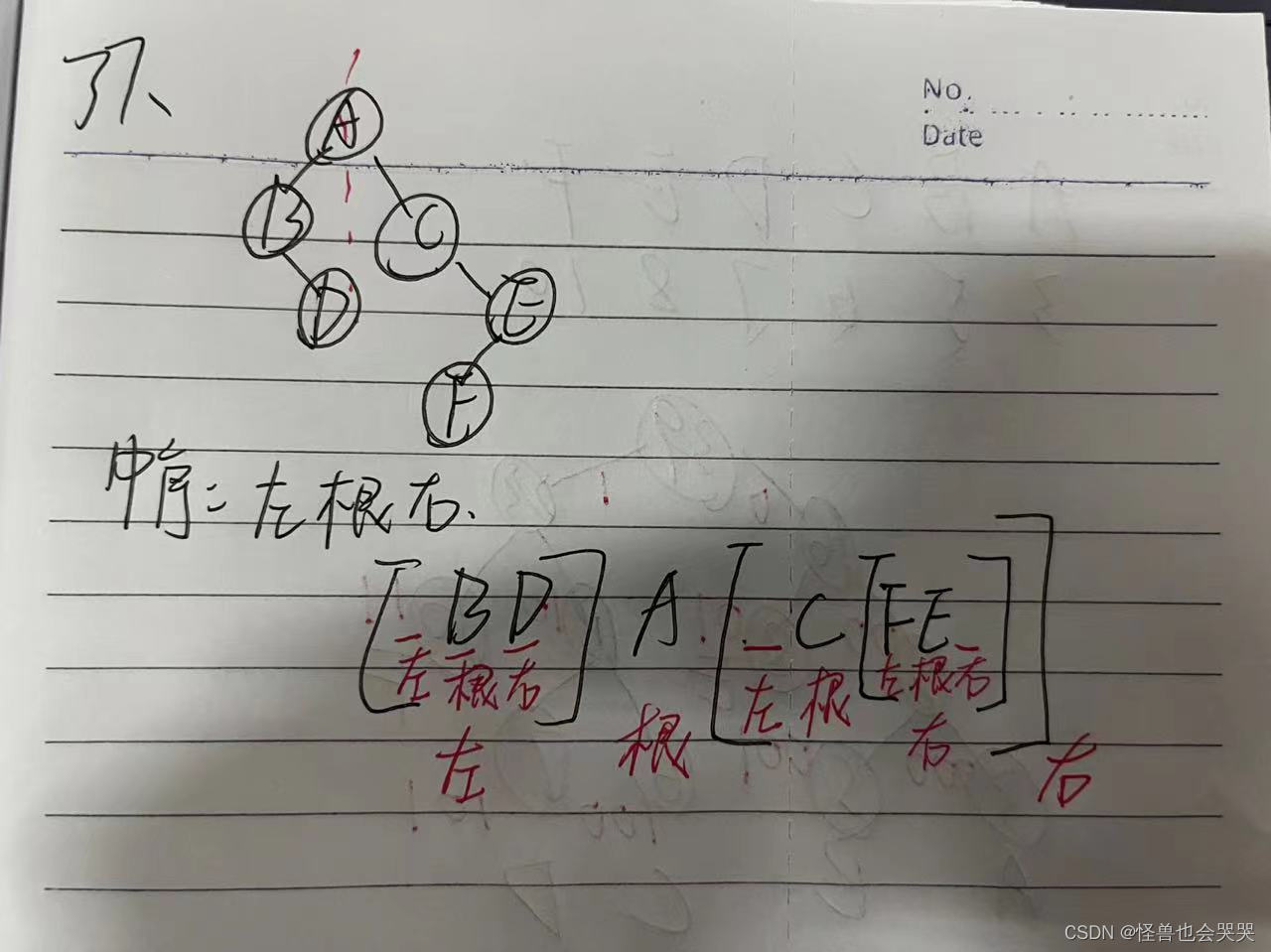
37.【填空题】——树:中序遍历序列
以下二叉树的中序遍历序列是 _BDACFE__ 。(答案不含空格)
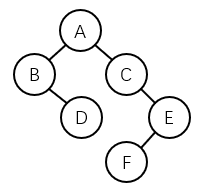
解题过程如下:
*38.【填空题】——树:结点判读
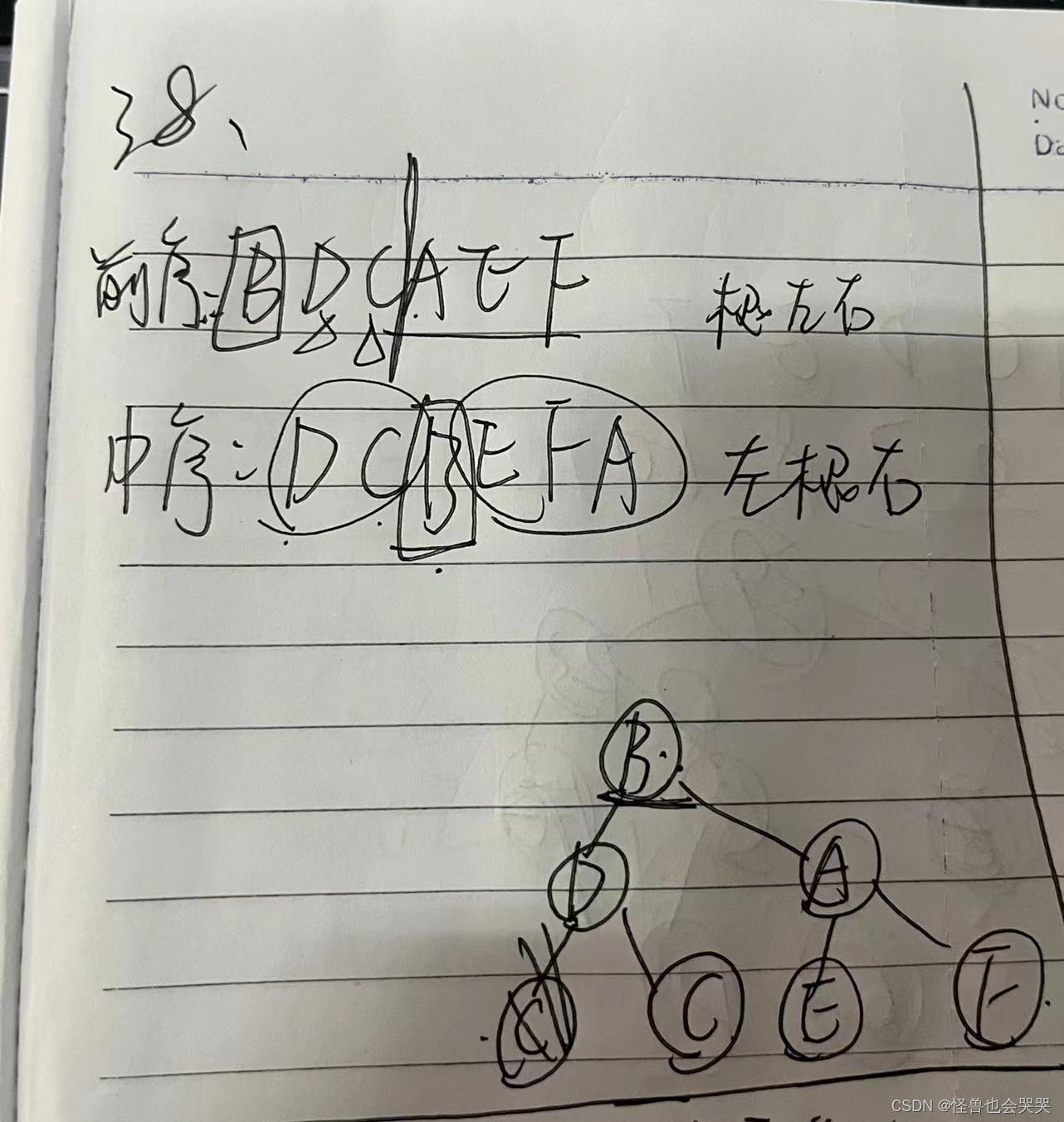
已知二叉树的前序遍历序列为BDCAEF,中序遍历序列为DCBEFA,则这颗二叉树中与结点E处于同一层次的是结点 _F__ 。C
解题过程如下:第一张是第一次做题的草稿,对完答案是错的。
问题在于:在构建结点B的右子树时,对于结点A的左右子树只考虑了前序,忽略了中序遍历序列,因此导致构建出的二叉树是一颗错的树。
这里附上正确的求解过程:
所以与结点E处于同一层的是结点C
39.【填空题】——二叉树:后序遍历算法
二叉树结点包含data数据域、left左指针域和right右指针域。以下是二叉树的后序遍历算法的实现,程序划线处应填入的语句是:__right_ 。

40.【填空题】 ——二叉树的深度
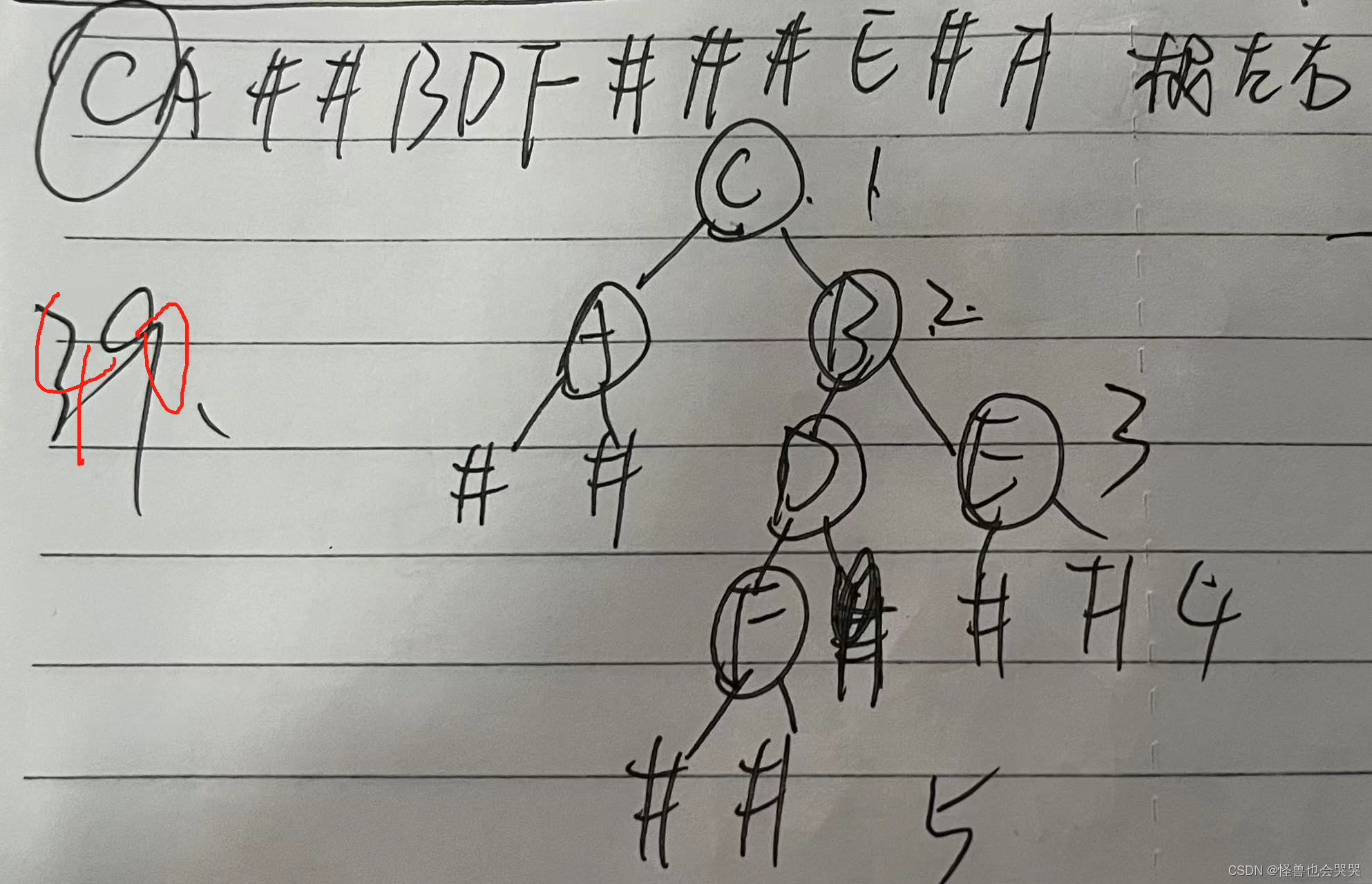
已知二叉树的带空树(#)位置的前序遍历序列为CA##BDF###E##,则这颗二叉树的深度是 __4_ (阿拉伯数字)。
解题过程如下:【最后标注的5是误写,那一层都是#,为空,不能算作一层】
41.【填空题】——二叉树:链式存储结构的指针域数目求解
一颗结点数为n的二叉树,在其链式存储结构中,共有 __n+1_ 个指针域可以设置为线索。(答案不含空格)
42.【填空题】 ——二叉树:指定结点的右孩子结点
对以下二叉树进行中序线索化,则结点F的右指针应指向结点 _C__。
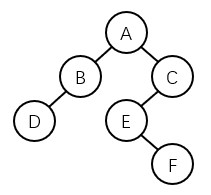
这道题的解题思路就是写出这棵树的中序遍历序列:DBAEFC
结点F的后继结点是C。
43.【填空题】——哈夫曼树:求带权路径长度
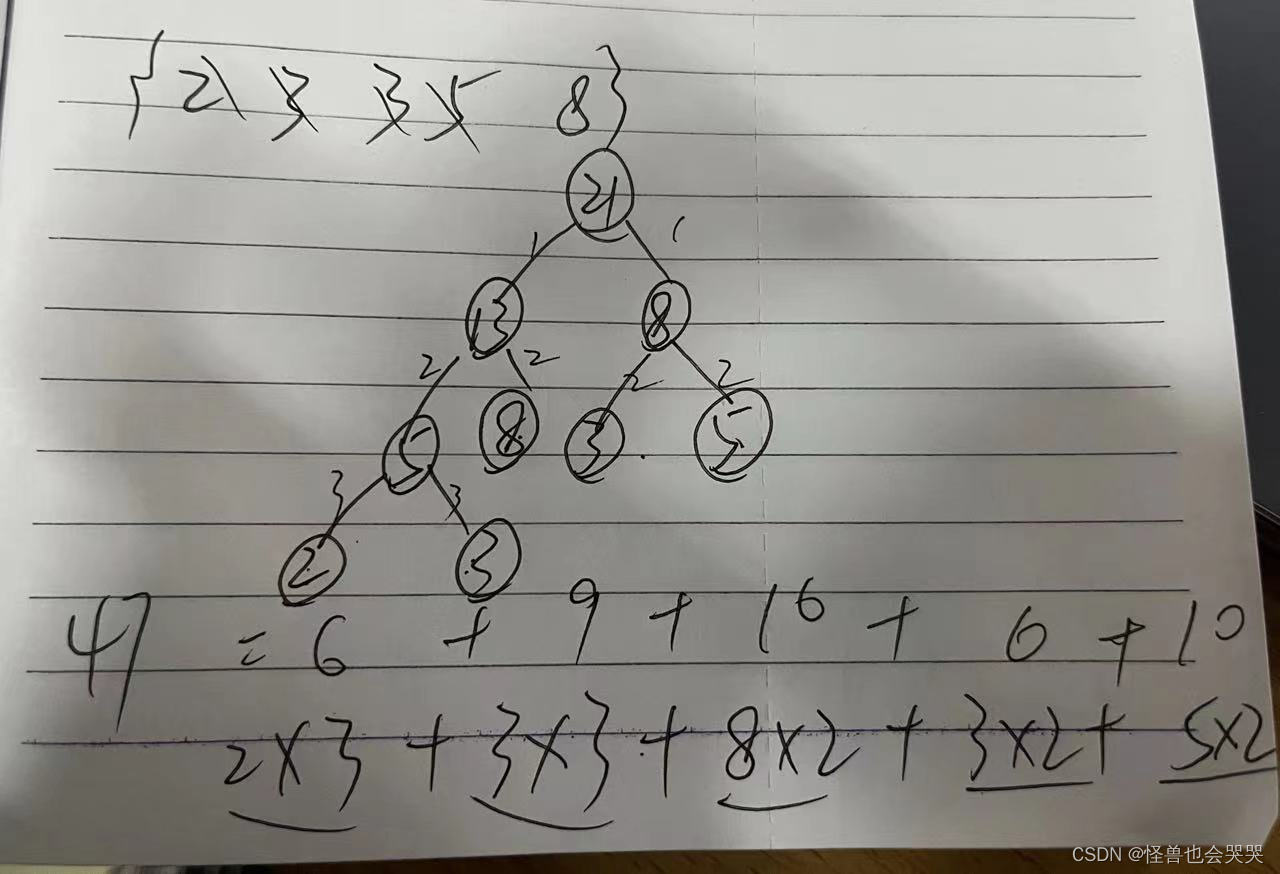
给定权值:2,3,3,5,8建立哈夫曼树,则这颗哈夫曼树的带权路径长度为 __47_ (阿拉伯数字)。
解题过程如下:
44.【填空题】——哈夫曼树:结点数目
已知哈夫曼树有n个叶子结点,则这颗哈夫曼树总共有 __2n-1_ 个结点 。
*45.【填空题】 ——字符的哈夫曼编码
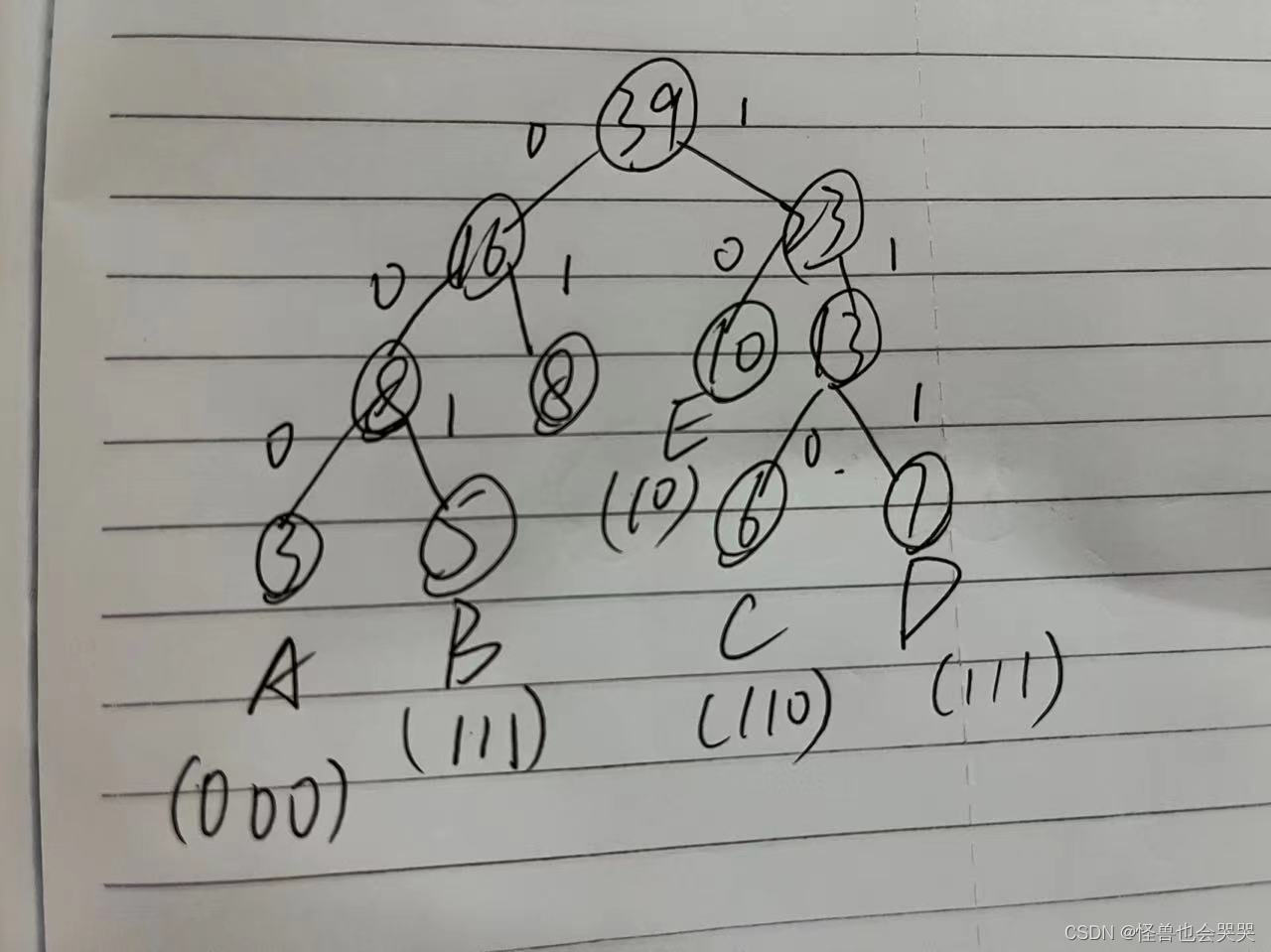
设在电文中包含的字符有: A,B,C,D,E,F,各字符出现的次数依次为:3,5,6,7,8,10。 设计哈夫曼编码以表示各字符,则字符C的哈夫曼编码为 _100__ 。110
解题过程如下:这里第一张是做题时的解题过程,但是做错了:
原因在于:结点(13)和结点(10)的位置放反了,在这道题我统一都是左小于等于右去构建哈夫曼树,但是在结点(39)的右子树结点(23)上,却将左右子树写反了
这里进行修正:
——图——
46.【填空题】——图的相关知识点
图中起点和终点相同的路径称为 __回路_ 。
47.【填空题】——图:邻接表存储结构的构成部分
图的邻接表存储结构,包含顶点表和 _边表__ 两部分。
48.【填空题】——图:遍历方法
在图的遍历方法中,与树的层次遍历类似的是图的 __广度_ 优先遍历方法。
49.【填空题】——生成树的边数求解
已知连通图共有1024个顶点,则其生成树有 __1023_ 条边。(阿拉伯数字)
生成树性质:n个顶点,n-1条边的连通子图
1024个顶点,那么对应就有1024-1=1023条边
50.【填空题】——最小生成树的算法
在求解连通图的最小生成树的算法中,初始时即选中全部顶点的算法称为 _克鲁斯卡尔__ (中文)算法。
相关文章:
数据结构第二次作业——递归、树、图【考点罗列//错题正解//题目解析】
目录 一、选择题 ——递归—— 1.【单选题】 ——递归的相关知识点 2.【单选题】——递归的应用 3.【单选题】——递归的实现结构 4.【单选题】——递归的执行与实现 5.【单选题】 ——递归算法 ——树—— 6.【单选题】 ——树的结构 *7.【单选题】——树的知识点 …...

Redis--12--Redis分布式锁的实现
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 Redis分布式锁最简单的实现如何避免死锁?锁被别人释放怎么办?锁过期时间不好评估怎么办?--看门狗分布式锁加入看门狗 redissonRe…...

MongoDB简介与安装
目录 1. MongoDB简介 2. 安装MongoDB 3. 基本命令行操作 4. Java代码实践 MongoDB是一种NoSQL数据库,以其灵活的文档存储模型和高度可扩展性而闻名。这篇文章将简单介绍一下MongoDB的基本概念,包括其特点和优势,并提供安装MongoDB的步骤。…...
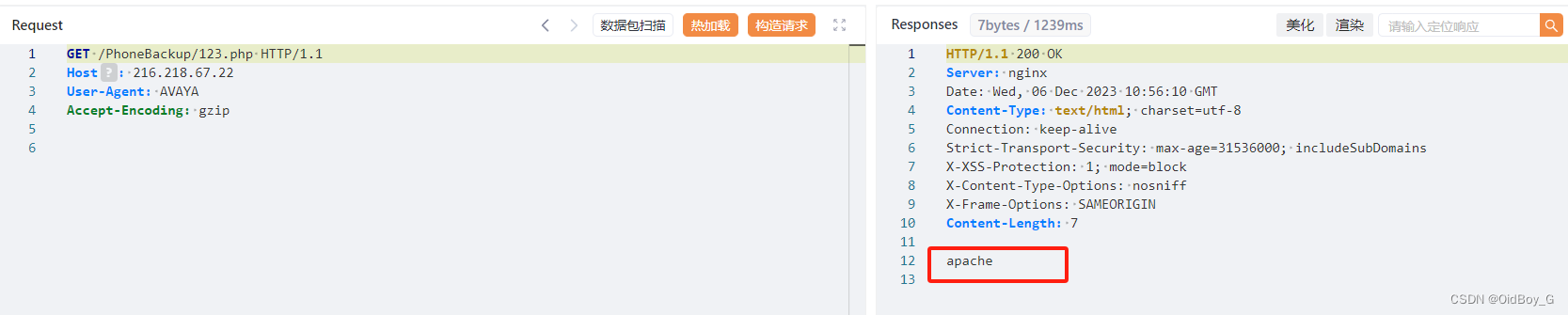
Avaya Aura Device Services 任意文件上传漏洞复现
0x01 产品简介 Avaya Aura Device Services是美国Avaya公司的一个应用软件。提供一个管理 Avaya 端点功能。 0x02 漏洞概述 Avaya Aura Device Services 系统PhoneBackup接口处存在任意文件上传漏洞,攻击者可绕过验证上传任意文件获取服务器权限。 0x03 影响范围…...
C#注册表技术及操作
目录 一、注册表基础 1.Registry和RegistryKey类 (1)Registry类 (2)RegistryKey类 二、在C#中操作注册表 1.读取注册表中的信息 (1)OpenSubKey()方法 (2)GetSubKeyNames()…...
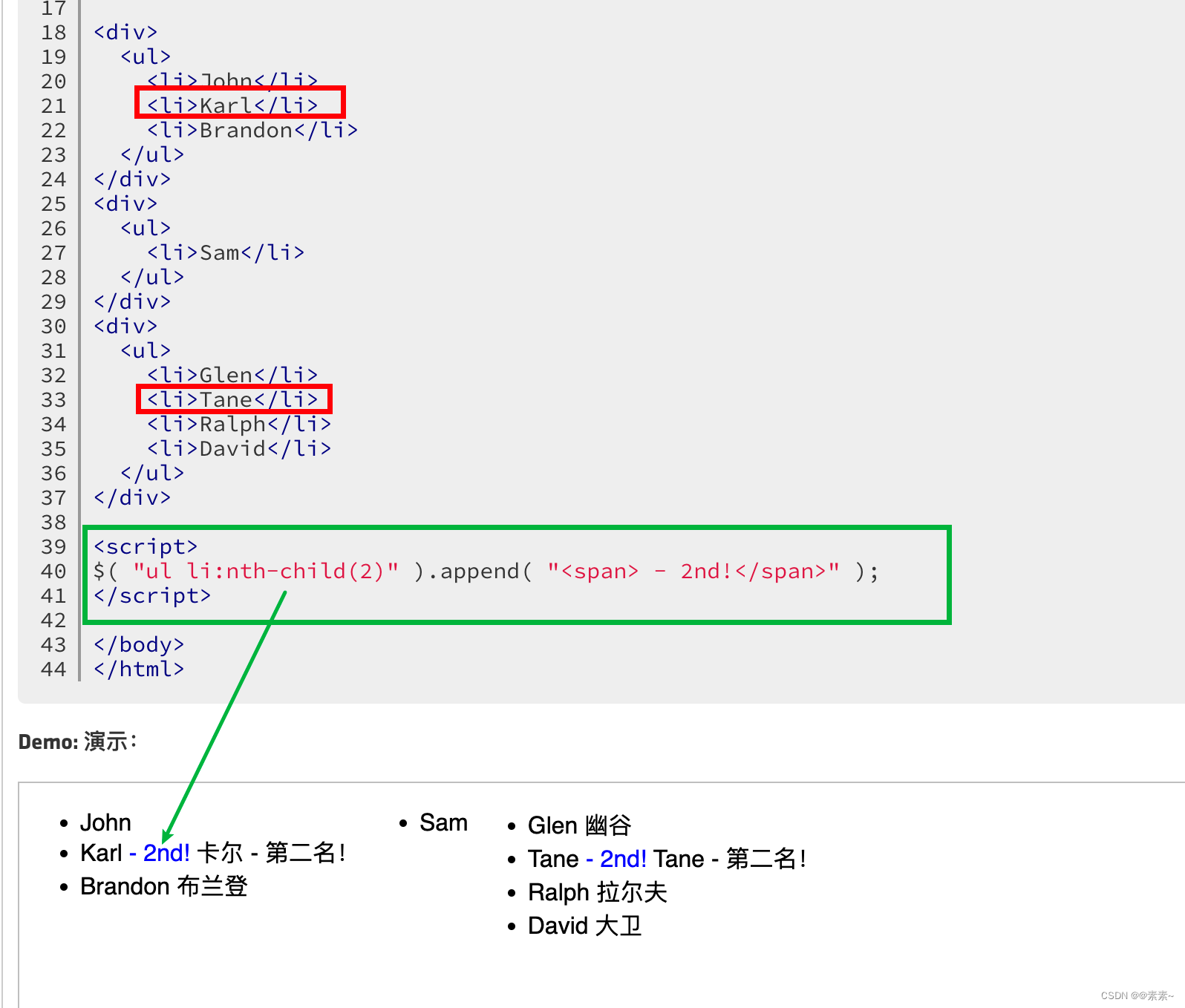
js/jQuery常见操作 之各种语法例子(包括jQuery中常见的与索引相关的选择器)
js/jQuery常见操作 之各种语法例子(包括jQuery中常见的与索引相关的选择器) 1. 操作table常见的1.1 动态给table添加title(指定td)1.1.1 给td动态添加title(含:获取tr的第几个td)1.1.2 动态加工…...
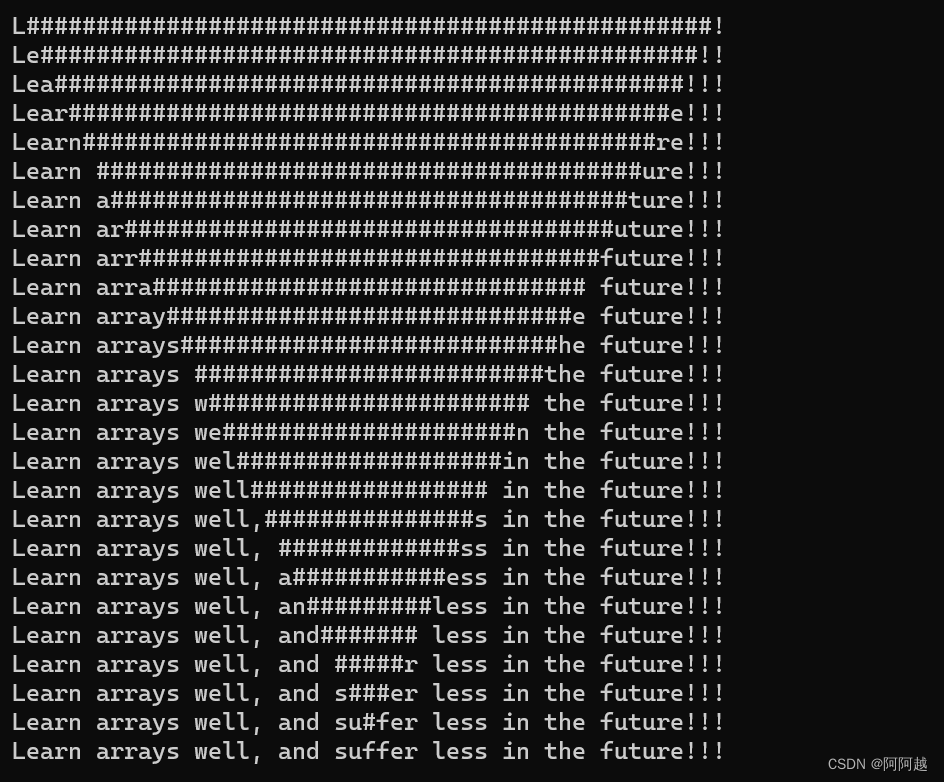
C语言数组(下)
我希望各位可以在思考之后去看本期练习,并且在观看之后独立编写一遍,以加深理解,巩固知识点。 练习一:编写代码,演⽰多个字符从两端移动,向中间汇聚 我们依旧先上代码 //编写代码,演⽰多个字…...

pytorch学习5-最大池化层的使用
系列文章目录 pytorch学习1-数据加载以及Tensorboard可视化工具pytorch学习2-Transforms主要方法使用pytorch学习3-torchvisin和Dataloader的使用pytorch学习4-简易卷积实现pytorch学习5-最大池化层的使用pytorch学习6-非线性变换(ReLU和sigmoid)pytorc…...

在python中安装库,会有conda安装,也会有pip安装,conda与pip的区别是什么?
文章目录 一、Conda是什么?二、pip是什么?三、pip与conda的区别:总结 一、Conda是什么? Conda是一个开源的包管理系统,它是Anaconda公司为Python和其他编程语言开发的。它主要用于数据科学和机器学习领域,…...
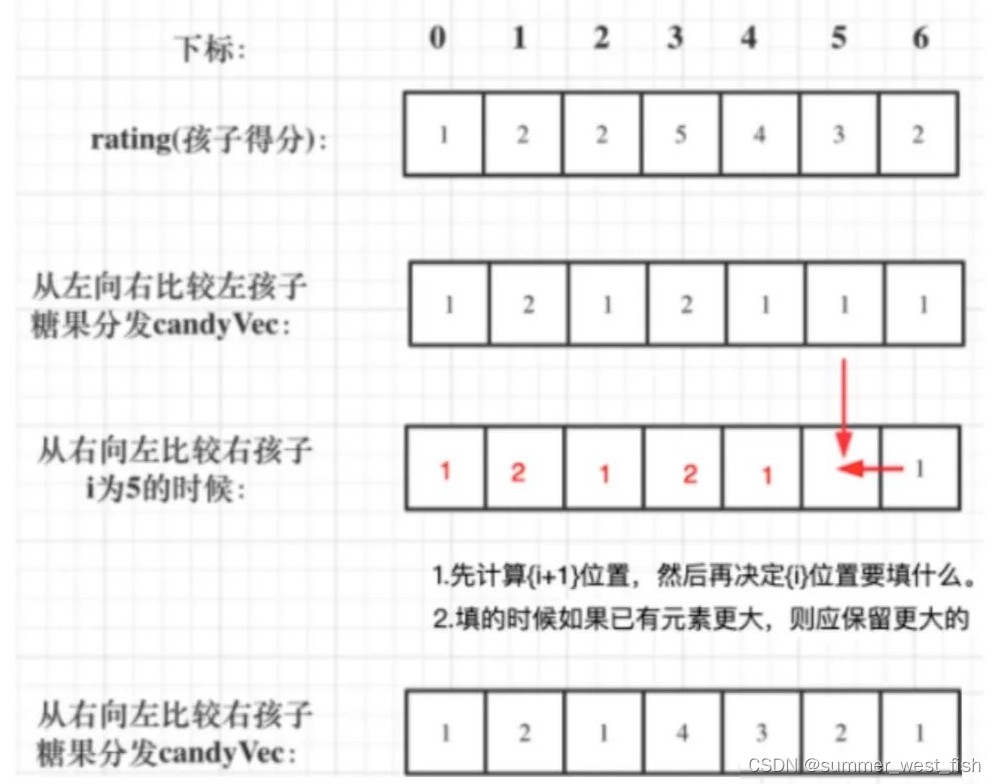
算法-贪心思想
贪心的思想非常不好解释,而且越使用权威的语言解释越难懂。而且做题的时候根据自己的理解可能直接做出来,但是非要解释一下怎么使用的贪心的话,就懵圈了。一般来说,贪心的题目没有固定的套路,一题一样,不过…...

STL源码剖析笔记——适配器(adapters)
系列文章目录 STL源码剖析笔记——迭代器 STL源码剖析笔记——vector STL源码剖析笔记——list STL源码剖析笔记——deque、stack,queue STL源码剖析笔记——Binary Heap、priority_queue STL源码剖析笔记——AVL-tree、RB-tree、set、map、mutiset、mutimap STL源…...

Mysql、Oracle区分大小写?
Mysql Windows 系统的文件名不区分大小写,所以运行在 Windows 系统上面的 MySQL 服务器也不用区分数据库名和表名的大小写。Linux 系统大小写规则: 数据库名与表名严格区分大小写表的别名严格区分大小写变量名严格区分大小写列名与列的别名忽略大小写 M…...
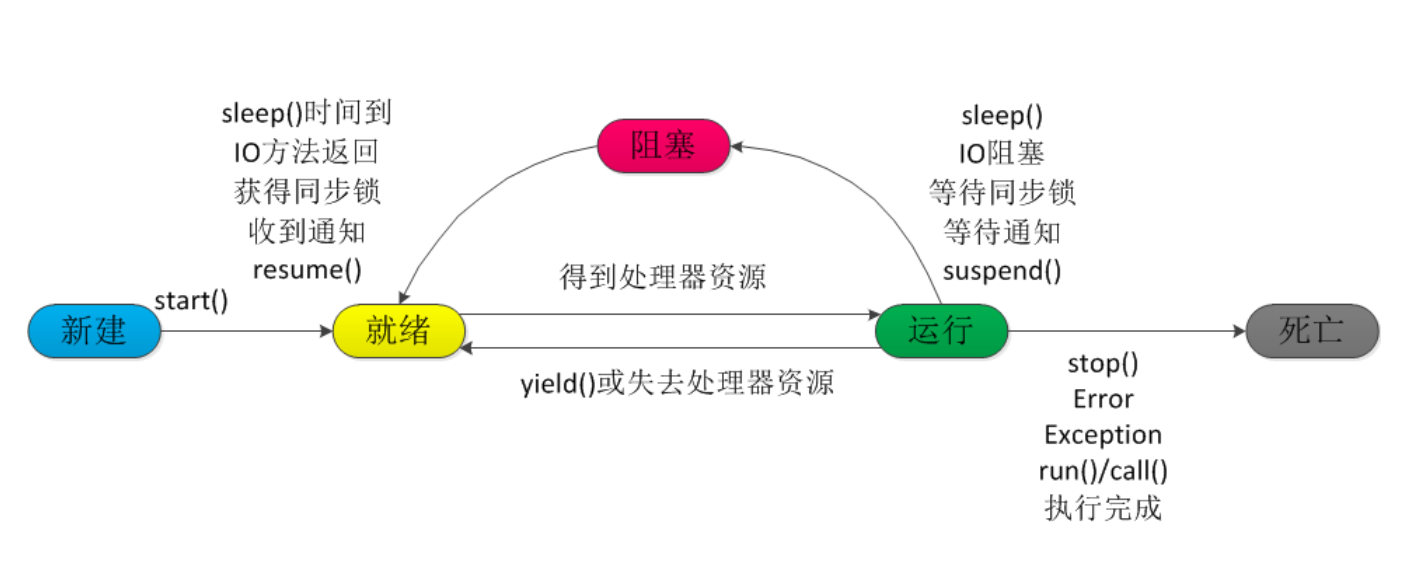
Java多线程并发(二)
四种线程池 Java 里面线程池的顶级接口是 Executor,但是严格意义上讲 Executor 并不是一个线程池,而只是一个执行线程的工具。真正的线程池接口是 ExecutorService。 newCachedThreadPool 创建一个可根据需要创建新线程的线程池,但是在以前…...

树莓派外接上显示器以后一直黑屏无画面显示
一般遇到这种情况都是因为没有强制支持热插拔引起的,先断电树莓派,确保显示器与树莓派连接正常,然后上电就可以正常显示了。 如果想要支持热插拔,可以修改配置文件。 sudo nano /boot/config.txt 修改如下配置 hdmi_force_hotpl…...

使用Ansible lineinfile模块进行行级别操作
Ansible是一种功能强大的自动化工具,它提供了各种模块来简化配置管理任务。其中,lineinfile模块是一种特别有用的模块,它允许我们在文件中插入、修改或删除行。本文将介绍Ansible的lineinfile模块,并演示如何使用它来进行行级别操…...

curl 18 HTTP/2 stream
cd /Users/haijunyan/Desktop/CustomKit/KeepThreadAlive/KeepThreadAlive //Podfile所在文件夹 git config --global https.postBuffer 10485760000 git config --global http.postBuffer 10485760000 pod install https://blog.csdn.net/weixin_41872403/article/details/86…...

5G+AI开花结果,助力智慧安检落地
“请带包的乘客过机安检!”,深圳地铁、腾讯共同打造的5GAI智慧安检辅助系统亮相福田枢纽站,进一步解放了人力,提高安检效率,为交通安全保驾护航,让智慧出行成为现实。 传统的安检设备均为人工肉眼辨识&…...

Swift 如何实现自定义 Tab Bar
前言 每个 UI 设计师都喜欢美丽而有动画效果的 Tab Bar。然而,对于开发人员来说,实现这种设计可能是一场噩梦。当然,使用 Apple 的原生 Tab Bar 组件并专注于更有趣的事情,比如业务逻辑的实现,会更容易。但如果我们必…...

mysql 语言学习
整理了一下 mysql 操作语言,不是很全,部分地方也许需要修改,先放上来,有时间再慢慢完善。 一、数据库操作 连接数据库 $ sudo mysql [-h ip] -u root -p [-P 3306] 初始化数据库 $ mysql_secure_installation备份数据库 # 备…...
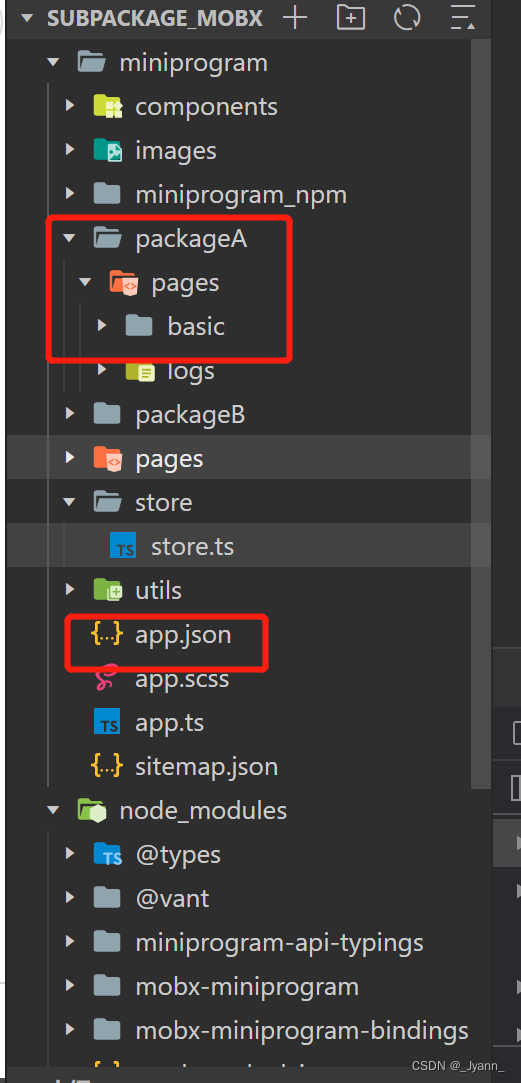
微信小程序基础bug
1.苹果11手机小程序请求数据不显示 设置-》隐私-》分析与改进-》开启 ”与开发者共享“ 2.<navigator>组件回退delta不成功 tabBar 页面是不能实现后退的效果的. 因为, 当我们跳转到 tabBar 页面,会关闭其他所有非tabBar 页面,所以当处于 tabBar 页面时, 无…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...