关于Pytorch和Numpy中的稀疏矩阵sparse的知识点
Pytorch和Numpy中的稀疏矩阵sparse
- 0 稀疏矩阵类别
- 0.1 coo_matrix
- 0.2 dok_matrix
- 0.3 csr_matrix
- 0.4 csc_matrix
- 0.5 bsr_matrix
- 0.6 bsc_matrix
- 0.7 lil_matrix
- 0.8 dia_matrix
- 1 pytorch中的稀疏矩阵
- 1.1 to_sparse()
- 1.2 to_sparse_csr()
- 1.3 sparse_coo_tensor()
- 1.4 sparse_csr_tensor()
- 1.5 sparse.sum()
- 1.6 sparse.mm()
- 2 numpy中的稀疏矩阵
- 参考博文及感谢
写在前面,pytorch和numpy都有对稀疏矩阵的操作,最大的区别在于pytorch可以通过GPU进行加速;不过现在numpy这边也推出了智能AI来加速对稀疏矩阵的运算;下面就稍微梳理一下关于稀疏矩阵的相关知识点,以飨诸君~
0 稀疏矩阵类别
不管是pytorch还是numpy,他们对稀疏矩阵的处理都是根据稀疏矩阵类别来的;所以先简单介绍稀疏矩阵的类别,这里网上已经有大量针对这些类别的详细解释说明,我这边就做引用:
SciPy 中不同稀疏矩阵存储方式介绍 (这个博客经常更换地址,而且加载不出图;但是是原创,所以贴出来);
不同稀疏矩阵存储方式介绍(这是对上面博客的CSDN转载,可看图)。
0.1 coo_matrix
对角存储矩阵(Coordinate Matrix)的简称
优:
能与CSR / CSC格式的快速转换
(tobsr()、tocsr()、to_csc()、to_dia()、to_dok()、to_lil())
缺:
不支持切片和算术运算操作
0.2 dok_matrix
按键字典矩阵(Dictionary of Keys Matrix)的简称
优:
对于递增的构建稀疏矩阵很高效,比如定义该矩阵后,想进行每行每列更新值,可用该矩阵。
可以高效访问单个元素,只需要O(1)
缺:
不允许重复索引(coo中适用),但可以很高效的转换成coo后进行重复索引
0.3 csr_matrix
压缩稀疏行矩阵(Compressed Sparse Row Matrix )的简称
优:
高效的稀疏矩阵算术运算
快速地矩阵矢量积运算
缺:
转换到稀疏结构代价较高(可以考虑LIL,DOK)
0.4 csc_matrix
压缩稀疏列矩阵(Compressed Sparse Column Matrix )的简称
优缺:
同上
0.5 bsr_matrix
分块压缩稀疏行矩阵(Block Sparse Row Matrix )的简称
优:
更适合于适用于具有密集子矩阵的稀疏矩阵
0.6 bsc_matrix
分块压缩稀疏列矩阵(Block Sparse Column Matrix )的简称
优:
更适合于适用于具有密集子矩阵的稀疏矩阵
0.7 lil_matrix
链表矩阵(Linked List Matrix )的简称
优:
适合递增的构建成矩阵
转换成其它存储方式很高效
支持灵活的切片
缺:
算术操作,列切片,矩阵向量内积操作慢(考虑用coo)
0.8 dia_matrix
对角存储矩阵(Diagonal Matrix)的简称
1 pytorch中的稀疏矩阵
先上官网开发文档镇楼TORCH.SPARSE 1.13 开发文档。
值得说明的是目前pytorch 只支持 COO, CSR, CSC, BSR, 和 BSC五种矩阵,可以用numpy转完在用pytorch。
这里首先讲pytorch而不是numpy的原因是pytorch确实比numpy快,具体看这里这个测试numpy, torch.spmm和torch.spmm 速度测试;
常用的方法有如下
1.1 to_sparse()
a = torch.tensor([[0, 2.], [3, 0]])
a.to_sparse()
官网有例子,不再重复造轮子;
1.2 to_sparse_csr()
1.3 sparse_coo_tensor()
1.4 sparse_csr_tensor()
crow_indices = torch.tensor([0, 2, 4])
col_indices = torch.tensor([0, 1, 0, 1])
values = torch.tensor([1, 2, 3, 4])
csr = torch.sparse_csr_tensor(crow_indices, col_indices, values, dtype=torch.float64)
csr
"""
tensor(crow_indices=tensor([0, 2, 4]),col_indices=tensor([0, 1, 0, 1]),values=tensor([1., 2., 3., 4.]), size=(2, 2), nnz=4,dtype=torch.float64)
"""
csr.to_dense()
"""
tensor([[1., 2.],[3., 4.]], dtype=torch.float64)
"""
1.5 sparse.sum()
1.6 sparse.mm()
这里提一句,torch.sparse.mm()和torch.spmm()是一样的,映射到的底层函数函数一样;具体可看这个numpy, torch.spmm和torch.spmm 稀疏矩阵乘法 测试;
2 numpy中的稀疏矩阵
照例搬出官方文档镇楼,Sparse matrices 1.11.4 官方文档
numpy是高性能科学计算和数据分析的基础包,其对稀疏矩阵的操作主要依赖于scipy开发包。
此处仍然引开篇的博客SciPy 中不同稀疏矩阵存储方式介绍
关于使用智能AI来加速对稀疏矩阵的运算,可参考此链接一行代码加速 sklearn 运算上千倍
PS:如果对numpy中的方法不熟,可以看这篇博客NumPy:数组批量计算
再贴一个numpy稀疏矩阵转pytorch的代码:
def sparse_mx_to_torch_sparse_tensor(sparse_mx):"""Convert a scipy sparse matrix to a torch sparse tensor."""if type(sparse_mx) != sp.coo_matrix:sparse_mx = sparse_mx.tocoo().astype(np.float32)indices = torch.from_numpy(np.vstack((sparse_mx.row, sparse_mx.col)).astype(np.int64))values = torch.from_numpy(sparse_mx.data).float()shape = torch.Size(sparse_mx.shape)return torch.sparse.FloatTensor(indices, values, shape)
参考博文及感谢
部分内容参考以下链接,这里表示感谢 Thanks♪(・ω・)ノ
参考博文1 Pytorch 关于稀疏矩阵 1.13 官方开发文档
https://pytorch.org/docs/1.13/sparse.html?highlight=sparse#module-torch.sparse
参考博文2 Numpy 关于稀疏矩阵 Sparse matrices 1.11.4 官方文档
https://docs.scipy.org/doc/scipy/reference/sparse.html
参考博文3 SciPy 中不同稀疏矩阵存储方式介绍
https://dreamhomes.github.io/posts/202012311027/
参考博文4 不同稀疏矩阵存储方式介绍
https://blog.csdn.net/DreamHome_S/article/details/111994423
参考博文5 numpy, torch.spmm和torch.spmm 稀疏矩阵乘法测试
https://github.com/rusty1s/pytorch_sparse/issues/356
参考博文6 一行代码加速 sklearn 运算上千倍
https://blog.csdn.net/dQCFKyQDXYm3F8rB0/article/details/125382907
相关文章:

关于Pytorch和Numpy中的稀疏矩阵sparse的知识点
Pytorch和Numpy中的稀疏矩阵sparse 0 稀疏矩阵类别0.1 coo_matrix0.2 dok_matrix0.3 csr_matrix0.4 csc_matrix0.5 bsr_matrix0.6 bsc_matrix0.7 lil_matrix0.8 dia_matrix 1 pytorch中的稀疏矩阵1.1 to_sparse()1.2 to_sparse_csr()1.3 sparse_coo_tensor()1.4 sparse_csr_ten…...
2024年AI云计算专题研究报告:智算带来的变化
今天分享的人工智能系列深度研究报告:《2024年AI云计算专题研究报告:智算带来的变化》。 (报告出品方:华泰证券) 报告共计:32页 Al 云计算 2024:关注智算带来的新变化 通过对海内外主要云厂商及其产业链…...
孩子还是有一颗网安梦——Bandit通关教程:Level 5 → Level 6
🕵️♂️ 专栏《解密游戏-Bandit》 🌐 游戏官网: Bandit游戏 🎮 游戏简介: Bandit游戏专为网络安全初学者设计,通过一系列级别挑战玩家,从Level0开始,逐步学习基础命令行和安全概念…...

vue2-elementUI部分组件样式修改
el-radio样式: /deep/ .el-radio__input .el-radio__inner {width: 20px;height: 20px;position: relative;cursor: pointer;-webkit-appearance: none;-moz-appearance: none;appearance: none;border: 1px solid #999;border-radius: 0;outline: none;transition…...

fijkplayer flutter 直播流播放
fijkplayer flutter 直播流播放 fijkplayer 是 ijkplayer 的 Flutter 封装, 是一款支持 android 和 iOS 的 Flutter 媒体播放器插件, 由 ijkplayer 底层驱动。 通过纹理(Texture)接入播放器视频渲染到 Flutter 中。 前言 目前使用…...
)
Javascript的基本语法(规范)
JS的基本语法规范 1.JS中严格区分大小写 2.JS中每一个指令被称为一个语句,每一个语句都应该以分号结尾 - 在JS中有自动的添加分号的机制,如果不写分号浏览器会自动为你添加 - 有些情况下,浏览器可能会给你加错了(几率低&#…...
vue chrome debugger 无效
昨天晚上debbger可以正常运行的,但是早上起来突然间所有的debugger都不会被命中,重装了vscode,也清了浏览器缓存,可是这个bitch还是不行!整整折腾了一早上,就是无法解决,没办法只能找找资料 ,搜…...

JRT实现Cache的驱动
我只给PostGreSql和iris写了连接驱动,永国的库是Cache,他就自己写了个驱动,驱动其实就是把数据库差异接口抽取了出来,然后只要配对应数据库驱动就能连响应的数据库了。 package JRT.Dal.Base;import JRT.Core.MultiPlatform.JRTC…...
)
ESP32网络开发实例-Web串口(WebSerial)
Web串口(WebSerial) 文章目录 Web串口(WebSerial)1、软件准备2、硬件准备3、代码实现4、接收数据在本文中,我们将介绍如何实现的基于 Web 的 ESP32 串行监视器。 1、软件准备 Arduino IDE在前面的文章中,如何搭建ESP32的Arduino IDE开环境,主参考: ESP32-Arduino-开发实…...
P2 Qt Creator创建第一个Qt程序
前言 🎬 个人主页:ChenPi 🐻推荐专栏1: 《C_ChenPi的博客-CSDN博客》✨✨✨ 🔥 推荐专栏2: 《LLinux C应用编程(概念类)_ChenPi的博客-CSDN博客》✨✨✨ 🌺本篇简介 :这一章我们学…...

加班、效率和价值
效率不等于单位时间单位人干的活,而是等于单位时间单位人产出的价值,衡量工作量的难度很大,而如何选择工作重点,挖掘工作价值难度更大。 加班的不可持续在于两点,第一点是对身体和精神的损害,降低内在动力…...

【QT 5 调试软件+(Linux下验证>>>>串口相关初试串口)+Windows下qt代码在Linux下运行+参考win下历程+基础样例】
【QT 5 调试软件Linux下验证>>>>串口相关初试串口参考win下历程基础样例】 1、前言2、实验环境3、先行了解4、自我总结-win下工程切到Linux下1、平台无关的代码:2、依赖的库:3、文件路径和换行符:4、编译器差异:5、构…...
地址栏不安全提示
在使用浏览器时访问网站的时候,我们可能会遇到地址栏提示不安全的情况。这种情况通常都是是由于未安装有效SSL证书或者网站SSL证书过期等原因导致的。本文将介绍如何处理地址栏提示不安全的问题,以确保我们的上网安全。 1,缺少SSL证书&#x…...

glib编译与实战
文章目录 下载编译修正实战参考 下载 https://ftp.acc.umu.se/pub/GNOME/sources/glib/ 编译 cd glib mkdir buildmeson --prefix/home/glib build ninja -C build ninja -C build install修正 meson.build:1:0: ERROR: Meson version is 0.53.2 but project requires >…...
)
PHP基础(4)
目录 一、PHP 创建用户定义函数 二、数组 数组的排序函数 一、PHP 创建用户定义函数 用户定义的函数声明以单词 "function" 开头: PHP自定义函数是指用户自行定义的函数,以满足自己的编程需求。在PHP中,可以通过以下语法来定义一…...
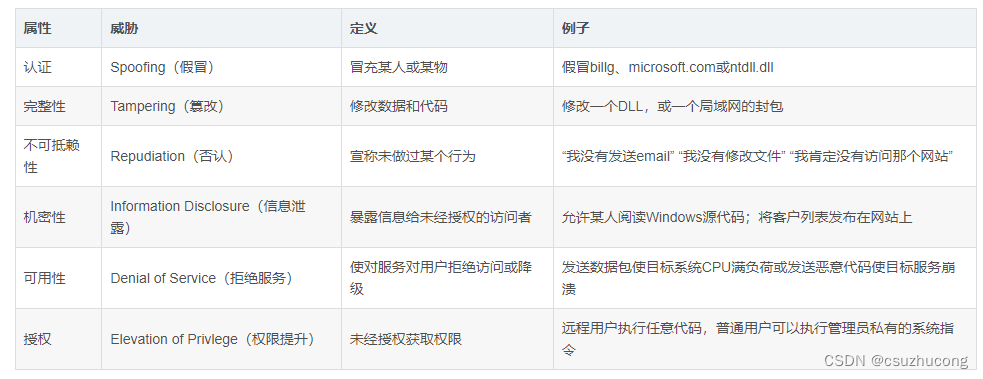
软件安全设计
目录 一,STRIDE 威胁建模 1,STRIDE 2,总体流程(关键步骤) 3,数据流图的4类元素 二,安全设计原则 三,安全属性 一,STRIDE 威胁建模 1,STRIDE STRIDE 是…...

Mysql、Oracle安全项检查表及操作脚本
软件开发全资料获取:点我获取 Mysql检查表 Oracle检查表...
单片双向马达驱动芯片D6208的芯片描述
D6208 是一块单片双向马达驱动电路,它使用TTL电平的逻辑信号就能控制卡式录音机和其它电子设备中的双向马达。该电路由一个逻辑部分和一个功率输出部分组成。逻辑部分控制马达正、反转向及制动,功率输出部分根据逻辑控制能提供100mA(典型值&a…...

使用ansible命令部署k8s集群
1.部署ansible集群 使用python脚本一个简单的搭建ansible集群-CSDN博客 2.ansible命令搭建k8s: 1.主机规划: 节点IP地址操作系统配置server192.168.174.150centos7.92G2核client1192.168.174.151centos7.92G2核client2192.168.174.152centos7.92G2核…...
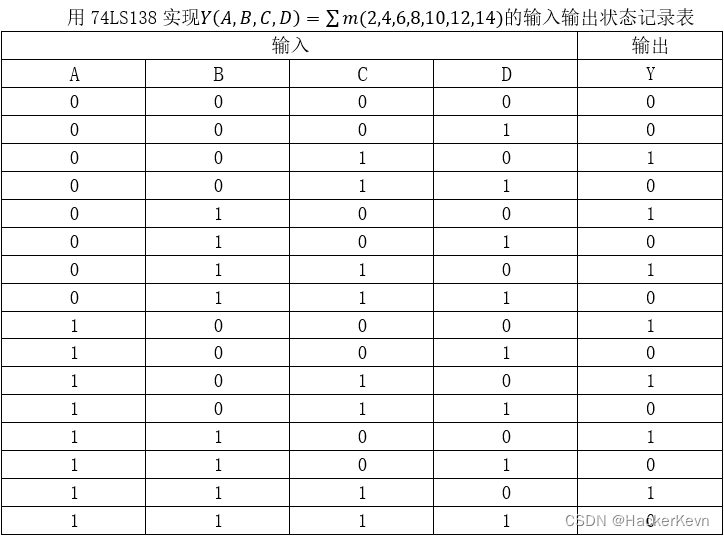
【上海大学数字逻辑实验报告】四、组合电路(三)
一、 实验目的 掌握多路选择器74LS151的原理。掌握译码器74LS138的原理。学会在Quartus II上使用多路选择74LS151设计电路。学会在Quartus II上使用译码器74LS138设计电路。 二、 实验原理 多路选择器又称数据选择器或多路开关,它是一种多路输入单路输出的组合逻…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...
