软件开发经常出现的bug原因有哪些
软件开发中出现bug的原因是多方面的,这些原因可能涉及到开发流程、人为因素、设计问题以及其他一系列因素。以下是一些常见的导致bug的原因:
1. 错误的需求分析: 不正确、不完整或者模糊的需求分析可能导致开发人员误解客户的需求,从而在实现过程中引入错误。
2. 设计缺陷: 不良的软件设计决策可能导致系统结构上的问题,增加了引入bug的可能性。
3. 编码错误: 开发人员在编写代码时可能会犯错,如语法错误、逻辑错误、数据类型错误等。
4. 集成问题: 在将各个模块或组件整合到一起时,可能会出现交互问题,导致bug。
5. 测试不足: 不充分或者不准确的测试可能无法捕捉到潜在的问题,让bug逃脱到最终产品中。
6. 时间压力: 迫于时间压力,开发人员可能会牺牲一些步骤,如测试或代码审查,从而增加引入bug的风险。
7. 人为疏忽: 开发人员可能因为疏忽大意而引入错误,比如复制粘贴错误、拼写错误等。
8. 环境问题: 软件可能在某些特定的操作系统、硬件或网络环境下出现问题,而这些问题在开发和测试阶段未能被完全考虑到。
9. 沟通问题: 缺乏有效的沟通和协作可能导致开发团队之间、开发团队与测试团队之间产生误解,从而引入bug。
10. 外部依赖: 如果软件依赖于外部库、框架或服务,这些外部组件的变化可能导致bug的出现。
为了降低bug的发生率,软件开发团队通常采用代码审查、单元测试、集成测试、用户验收测试等方法,并强调清晰的需求文档和有效的沟通。
相关文章:

软件开发经常出现的bug原因有哪些
软件开发中出现bug的原因是多方面的,这些原因可能涉及到开发流程、人为因素、设计问题以及其他一系列因素。以下是一些常见的导致bug的原因: 1. 错误的需求分析: 不正确、不完整或者模糊的需求分析可能导致开发人员误解客户的需求࿰…...
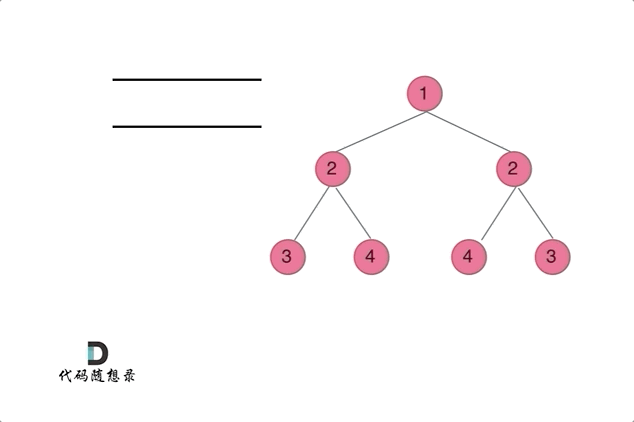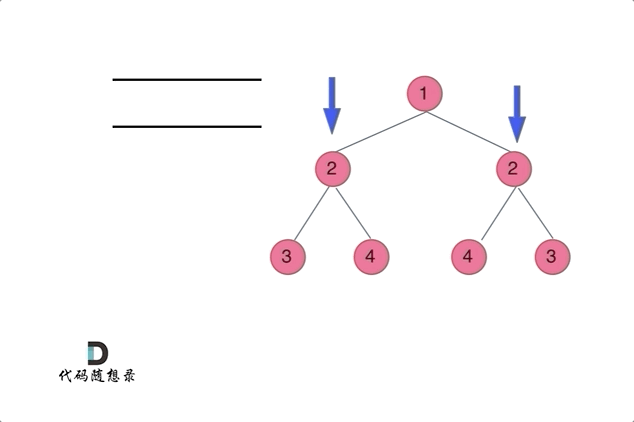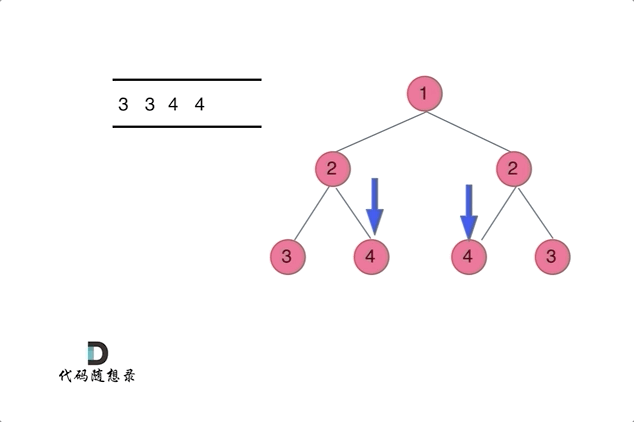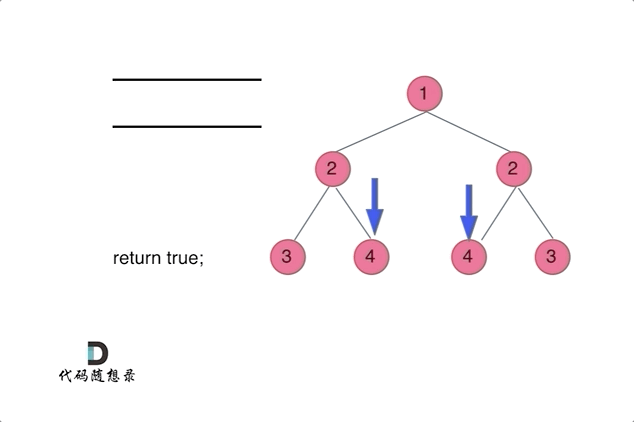
代码随想录27期|Python|Day15|二叉树|层序遍历|对称二叉树|翻转二叉树
本文图片来源:代码随想录 层序遍历(图论中的广度优先遍历) 这一部分有10道题,全部可以套用相同的层序遍历方法,但是需要在每一层进行处理或者修改。 102. 二叉树的层序遍历 - 力扣(LeetCode) 层…...
鸿蒙开发组件之Web
一、加载一个url myWebController: WebviewController new webview.WebviewControllerbuild() {Column() {Web({src: https://www.baidu.com,controller: this.myWebController})}.width(100%).height(100%)} 二、注意点 2.1 不能用Previewer预览 Web这个组件不能使用预览…...

成绩分析。
成绩分析 题目描述 小蓝给学生们组织了一场考试,卷面总分为 100分,每个学生的得分都是一个0到100的整数。 请计算这次考试的最高分、最低分和平均分 输入描述 输入的第一行包含一个整数n(1n104),表示考试人数。 接下来n行,每行包含…...
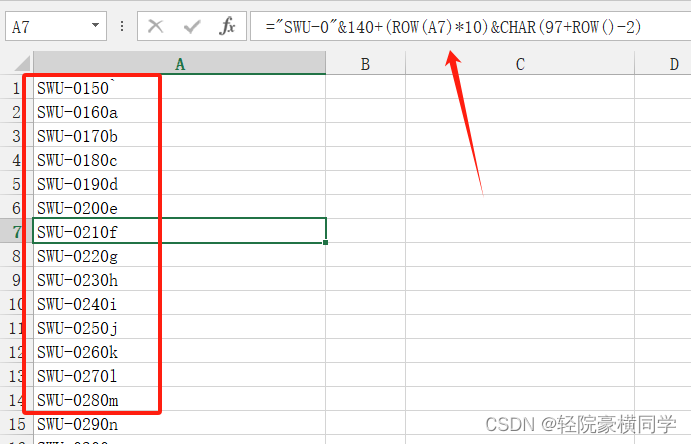
Excel实现字母+数字拖拉自动递增,步长可更改
目录 1、带有字母的数字序列自增加(步长可变) 2、仅字母自增加 3、字母数字同时自增 1、带有字母的数字序列自增加(步长可变) 使用Excel通常可以直接通过拖拉的方式,实现自增数字…...

Java之Stream流
一、什么是Stream流 Stream是一种处理集合(Collection)数据的方式。Stream可以让我们以一种更简洁的方式对集合进行过滤、映射、排序等操作。 二、Stream流的使用步骤 先得到一条Stream流,并把数据放上去利用Stream流中的API进行各种操作 中间…...

vue中element-ui日期选择组件el-date-picker 清空所选时间,会将model绑定的值设置为null 问题 及 限制起止日期范围
一、问题 在Vue中使用Element UI的日期选择组件 <el-date-picker>,当你清空所选时间时,组件会将绑定的 v-model 值设置为 null。这是日期选择器的预设行为,它将清空所选日期后将其视为 null。但有时后端不允许日期传空。 因此ÿ…...
使用模方时,三维模型在su中显示不了怎么办?
答:可以借助截图功能截取模型影像在su中绘制白模。 模方是一款针对实景三维模型的冗余碎片、水面残缺、道路不平、标牌破损、纹理拉伸模糊等共性问题研发的实景三维模型修复编辑软件。模方4.1新增自动单体化建模功能,支持一键自动提取房屋结构ÿ…...
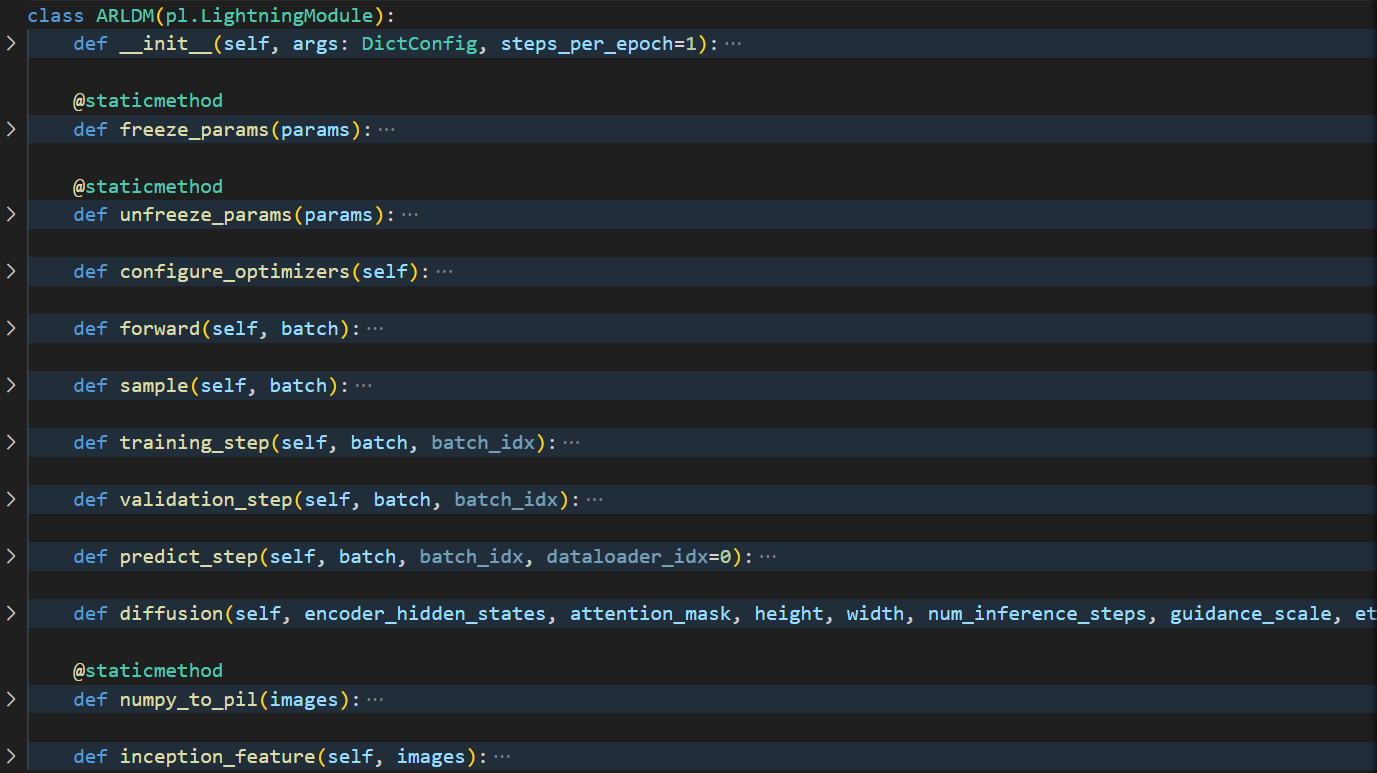
AR-LDM原理及代码分析
AR-LDM原理AR-LDM代码分析pytorch_lightning(pl)的hook流程main.py 具体分析TrainSampleLightningDatasetARLDM blip mm encoder AR-LDM原理 左边是模仿了自回归地从1, 2, ..., j-1来构造 j 时刻的 frame 的过程。 在普通Stable Diffusion的基础上,使用了1, 2, .…...

MySQL常见死锁的发生场景以及如何解决
死锁的产生是因为满足了四个条件: 互斥占有且等待不可强占用循环等待 这个网站收集了很多死锁场景 接下来介绍几种常见的死锁发生场景。其中,id 为主键,no(学号)为二级唯一索引,name(姓名&am…...
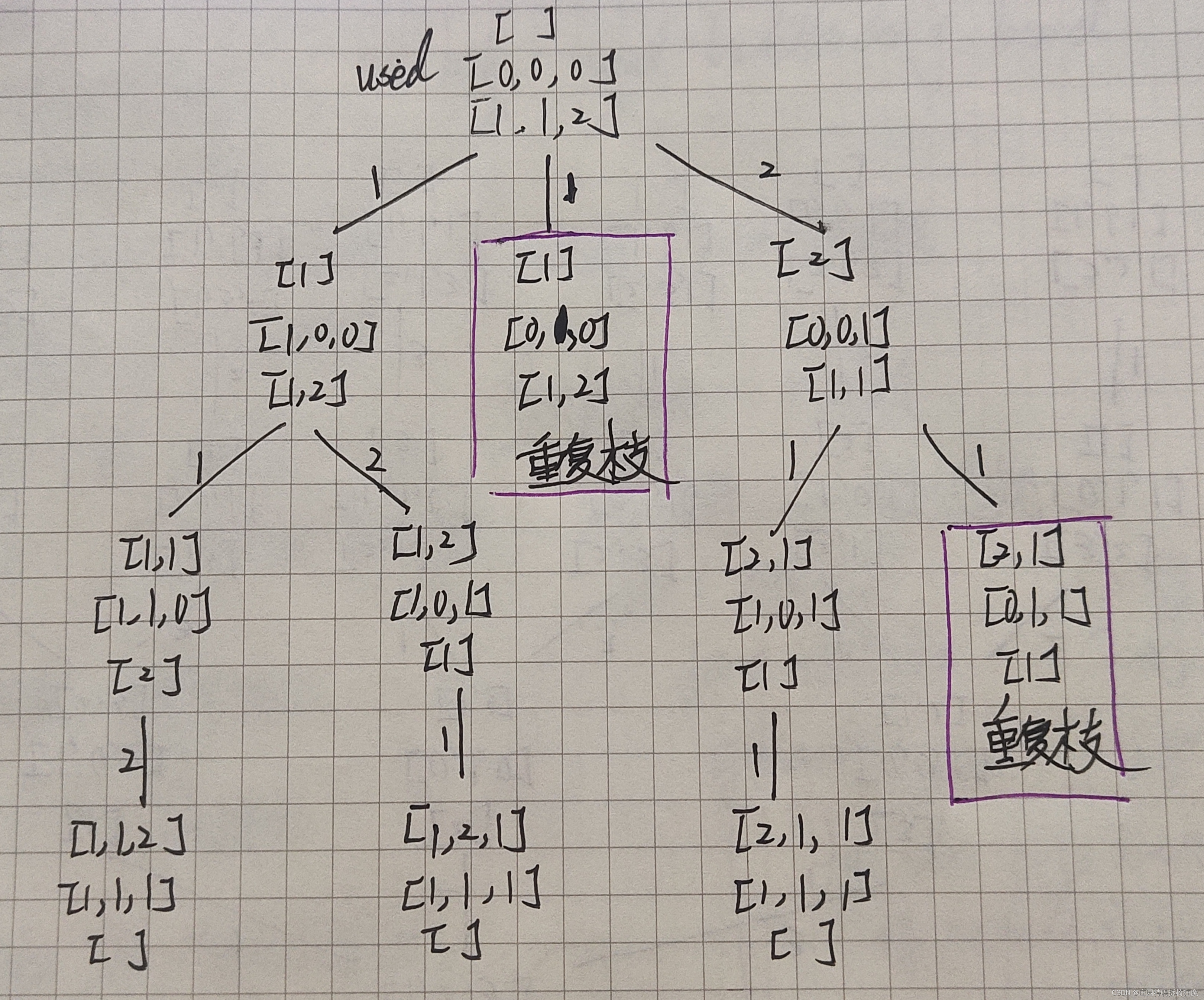
Leetcode 47 全排列 II
题意理解: 首先理解全排列是什么?全排列:使用集合中所有元素按照不同元素进行排列,将所有的排列结果的集合称为全排列。 这里的全排列难度升级了,问题在于集合中的元素是可以重复的。 问题:相同的元素会导致…...
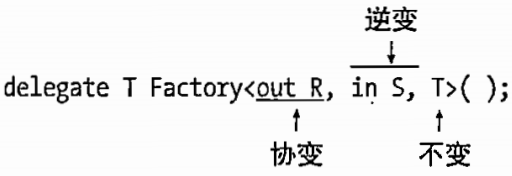
C# 图解教程 第5版 —— 第18章 泛型
文章目录 18.1 什么是泛型18.2 C# 中的泛型18.3 泛型类18.3.1 声明泛型类18.3.2 创建构造类型18.3.3 创建变量和实例18.3.4 使用泛型的示例18.3.5 比较泛型和非泛型栈 18.4 类型参数的约束18.4.1 Where 子句18.4.2 约束类型和次序 18.5 泛型方法18.5.1 声明泛型方法18.5.2 调用…...

保障事务隔离级别的关键措施
目录 引言 1. 锁机制的应用 2. 多版本并发控制(MVCC)的实现 3. 事务日志的记录与恢复 4. 数据库引擎的实现策略 结论 引言 事务隔离级别是数据库管理系统(DBMS)中的一个关键概念,用于控制并发事务之间的可见性。…...

Docker导入导出镜像、导入导出容器的命令详解以及使用的场景
一、Docker 提供用于管理镜像和容器命令 1.1 docker save 与 docker load 这是一对操作,用于处理 Docker 镜像。这个操作会将所有的镜像层以及元数据打包到一个 tar 文件中。然后,你可以使用 docker load 命令将这个 tar 文件导入到任何 Docker 环境中…...
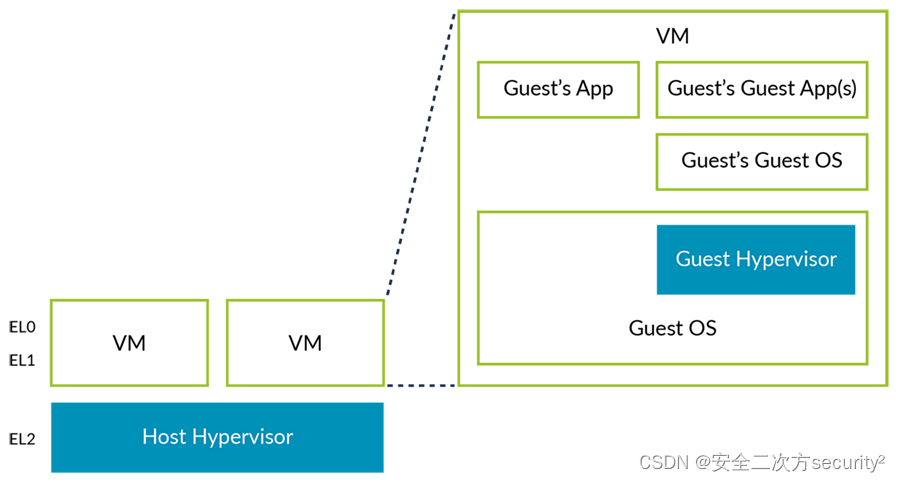
虚拟化嵌套
在理论上,可以在虚拟机(VM)内运行一个hypervisor,这个概念被称为嵌套虚拟化: 我们将第一个hypervisor称为Host Hypervisor,将VM内的hypervisor称为Guest Hypervisor。 在Armv8.3-A发布之前,可以通过在EL0中运行Guest Hypervisor来在VM中运行Guest Hypervisor。然而,这…...

【XILINX】记录ISE/Vivado使用过程中遇到的一些warning及解决方案
前言 XILINX/AMD是大家常用的FPGA,但是在使用其开发工具ISE/Vivado时免不了会遇到很多warning,(大家是不是发现程序越大warning越多?),并且还有很多warning根据消除不了,看着特心烦? 我这里汇总一些我遇到的…...
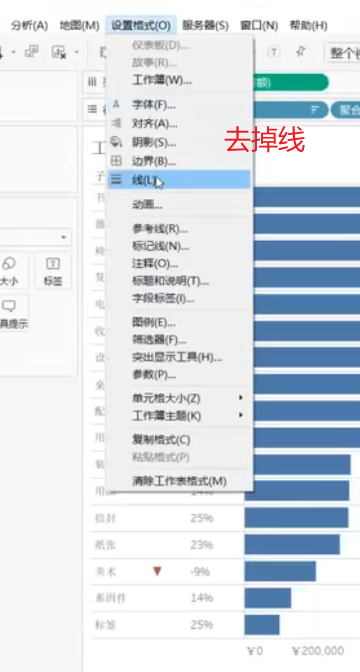
Tableau进阶--Tableau数据故事慧(20)解构Tableau的绘图逻辑
官网介绍 官网连接如下: https://www.tableau.com/zh-cn tableau的产品包括如下: 参考:https://zhuanlan.zhihu.com/p/341882097 Tableau是功能强大、灵活且安全些很高的端到端的数据分析平台,它提供了从数据准备、连接、分析、协作到查阅…...
)
45.0/HTML 简介(详细版)
目录 45.1 互联网简介 45.2 网页技术与分类 45.3 HTML 简介 45.3.1 什么是 HTML?(面试题) 45.3.2 HTML 文件结构 45.3.3 HTML 语法 45.3.4 实例演练步骤(面试题) 45.4 head 中的常用标签 45.4.1 title 标记 45.4.2 meta 标记 45.4.3 45.4.4 45.4.4(面试题)总结: 45…...

Python 如何进行游戏开发?
游戏开发是一个广泛的领域,Python 作为一门灵活的编程语言,可以用于不同类型的游戏开发。以下是一些建议和步骤,帮助你开始使用 Python 进行游戏开发: 1、选择游戏开发库/框架: Pygame: Pygame 是一个用于…...

到底什么是DevOps
DevOps不是一组工具,也不是一个特定的岗位。在我看来DevOps更像是一种软件开发文化,一种实现快速交付能力的手段。 DevOps 强调的是高效组织团队之间如何通过自动化的工具协作和沟通来完成软件的生命周期管理,从而更快、更频繁地交付更稳定的…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

《Offer来了:Java面试核心知识点精讲》大纲
文章目录 一、《Offer来了:Java面试核心知识点精讲》的典型大纲框架Java基础并发编程JVM原理数据库与缓存分布式架构系统设计二、《Offer来了:Java面试核心知识点精讲(原理篇)》技术文章大纲核心主题:Java基础原理与面试高频考点Java虚拟机(JVM)原理Java并发编程原理Jav…...

大数据驱动企业决策智能化的路径与实践
📝个人主页🌹:慌ZHANG-CSDN博客 🌹🌹期待您的关注 🌹🌹 一、引言:数据驱动的企业竞争力重构 在这个瞬息万变的商业时代,“快者胜”的竞争逻辑愈发明显。企业如何在复杂环…...
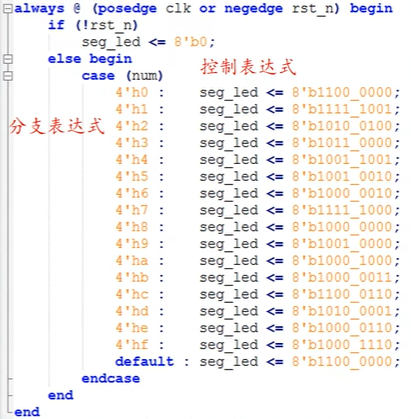
ZYNQ学习记录FPGA(二)Verilog语言
一、Verilog简介 1.1 HDL(Hardware Description language) 在解释HDL之前,先来了解一下数字系统设计的流程:逻辑设计 -> 电路实现 -> 系统验证。 逻辑设计又称前端,在这个过程中就需要用到HDL,正文…...

从0开始学习R语言--Day17--Cox回归
Cox回归 在用医疗数据作分析时,最常见的是去预测某类病的患者的死亡率或预测他们的结局。但是我们得到的病人数据,往往会有很多的协变量,即使我们通过计算来减少指标对结果的影响,我们的数据中依然会有很多的协变量,且…...
