机器学习-聚类问题
前言
聚类算法又叫做”无监督分类“,目标是通过对无标记训练样本来揭示数据的内在性质及 规律,为进一步的数据分析提供基础。
Kmeans
作为聚类算法的典型代表,Kmeans可以说是最简单的聚类算法,没有之一,那她是怎么完成聚类的呢?
- 算法接受参数k
- 给定样本集 D = { x 1 , x 2 , . . . , x n } D=\{x_1,x_2,...,x_n\} D={x1,x2,...,xn}
- 随机选点k个中心(质心)
- 遍历样本集,先取距离最近的质心,从而根据质心分解样本集D簇划分 C = { C 1 , C 2 , . . . , C k } C=\{C_1,C_2,...,C_k\} C={C1,C2,...,Ck}
- 最小化平方误差

- 利用簇中均值等方法更新该簇类的中心k个;
- 重覆4-6的步骤,直至E不再更新
Kmeans中用的是欧式距离
kmeans的计算过程
- 现在有4组数据,每组数据有2个维度,对其进行聚类分为2类,将其可视化一下。

- 通过比较,将其进行归类。并使用平均法更新中心位置。

- 再次计算每个点与更新后的位置中心的距离,直到上一次的类别标记无变化,即可停止
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs## 创建数据集
X, _ = make_blobs(n_samples=10000, centers=2, random_state=0)## kmeans超参数值列表
n_clusters_list = [4, 8, 16]# 图的框架
fig, axs = plt.subplots(1, len(n_clusters_list), figsize=(12, 5)
)
axs = axs.T
for j, n_clusters in enumerate(n_clusters_list):## 创建模型algo = KMeans(n_clusters=n_clusters, random_state=random_state, n_init=3)algo.fit(X)centers = algo.cluster_centers_axs[j].scatter(X[:, 0], X[:, 1], s=10, c=algo.labels_)## 画质心axs[j].scatter(centers[:, 0], centers[:, 1], c="r", s=20)axs[j].set_title(f"{n_clusters} clusters")
for ax in axs.flat:ax.label_outer()ax.set_xticks([])ax.set_yticks([])
plt.show()
聚类算法用于降维
K-Means聚类最重要的应用之一是非结构数据(图像,声音)上的矢量量化(VQ)。非结构化数据往往占用比较多的储存空间,文件本身也会比较大,运算非常缓慢,我们希望能够在保证数据质量的前提下,尽量地缩小非结构化数据的大小,或者简化非结构化数据的结构。
- 一组40个样本的数据,分别含有40组不同的信息(x1,x2)。
- 将代表所有样本点聚成4类,找出四个质心.这些点和他们所属的质心非常相似,因此他们所承载的信息就约等于他们所在的簇的质心所承载的信息。
- 使用每个样本所在的簇的质心来覆盖原有的样本,有点类似四舍五入的感觉,类似于用1来代替0.9和0.8。
这样,40个样本带有的40种取值,就被我们压缩了4组取值,虽然样本量还是40个,但是这40个样本所带的取值其实只有4个,就是分出来的四个簇的质心。查看官方用例
主要参考
《机器学习理论(十三)Kmeans聚类》
相关文章:

机器学习-聚类问题
前言 聚类算法又叫做”无监督分类“,目标是通过对无标记训练样本来揭示数据的内在性质及 规律,为进一步的数据分析提供基础。 Kmeans 作为聚类算法的典型代表,Kmeans可以说是最简单的聚类算法,没有之一,那她是怎么完…...

leetcode9.回文数java解法
力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 给你一个整数 x ,如果 x 是一个回文整数,返回 true ;否则,返回 false 。 回文数是指正序(从左向右)和倒序(从右向左&…...
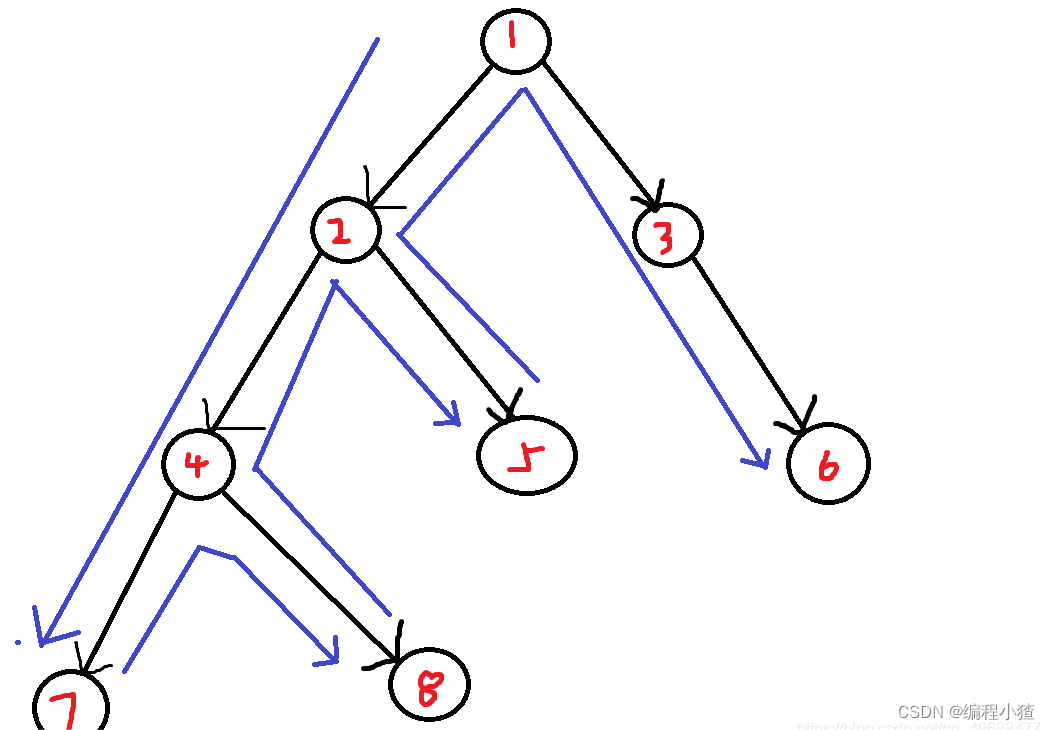
图论专栏一《图的基础知识》
图论(Graph Theory)是数学的一个分支。它以图为研究对象。图论中的图是由若干给定的点及连接两点的线所构成的图形,这种图形通常用来描述某些实体之间的某种特定关系,用点代表实体,用连接两点的线表示两个实体间具有的…...

得帆云为玉柴打造CRM售后服务管理系统,实现服务全过程管理|基于得帆云低代码的CRM案例系列
广西玉柴机器股份有限公司 广西玉柴机器股份有限公司始建于1992年,是国内行业首家赴境外上市的中外合资企业,产品远销亚欧美非等180多个国家和地区。公司总部设在广西玉林市,下辖11家子公司,生产基地布局广西、江苏、安徽、山东等…...

智能优化算法应用:基于蝠鲼觅食算法3D无线传感器网络(WSN)覆盖优化 - 附代码
智能优化算法应用:基于蝠鲼觅食算法3D无线传感器网络(WSN)覆盖优化 - 附代码 文章目录 智能优化算法应用:基于蝠鲼觅食算法3D无线传感器网络(WSN)覆盖优化 - 附代码1.无线传感网络节点模型2.覆盖数学模型及分析3.蝠鲼觅食算法4.实验参数设定5.算法结果6.…...

vue2 以及 vue3 自定义组件使用 v-model使用默认值以及自定义事件
vue2 以及 vue3 自定义组件使用 v-model使用默认值以及自定义事件 1. vue2 自定义组件的 v-model vue2官网,自定义组件官方解释:一个组件上的 v-model 默认会利用名为 value 的 prop 和名为 input 的事件上代码代码中使用了 element-ui 子组件 使用默…...
《PCL多线程加速处理》-滤波-统计滤波
《PCL多线程加速处理》-滤波-统计滤波 一、效果展示二、实现方式三、代码一、效果展示 提升速度随着点云越多效果越明显 二、实现方式 1、原始的统计滤波实现方式 #include <pcl/filters/statistical_outlier_removal.h>pcl::PointCloud<pcl::PointXYZ...

插入排序——直接插入排序和希尔排序(C语言实现)
文章目录 前言直接插入排序基本思想特性总结代码实现 希尔排序算法思想特性总结代码实现 前言 本博客插入排序动图和希尔排序视频参考大佬java技术爱好者,如有侵权,请联系删除。 直接插入排序 基本思想 直接插入排序是一种简单的插入排序法ÿ…...
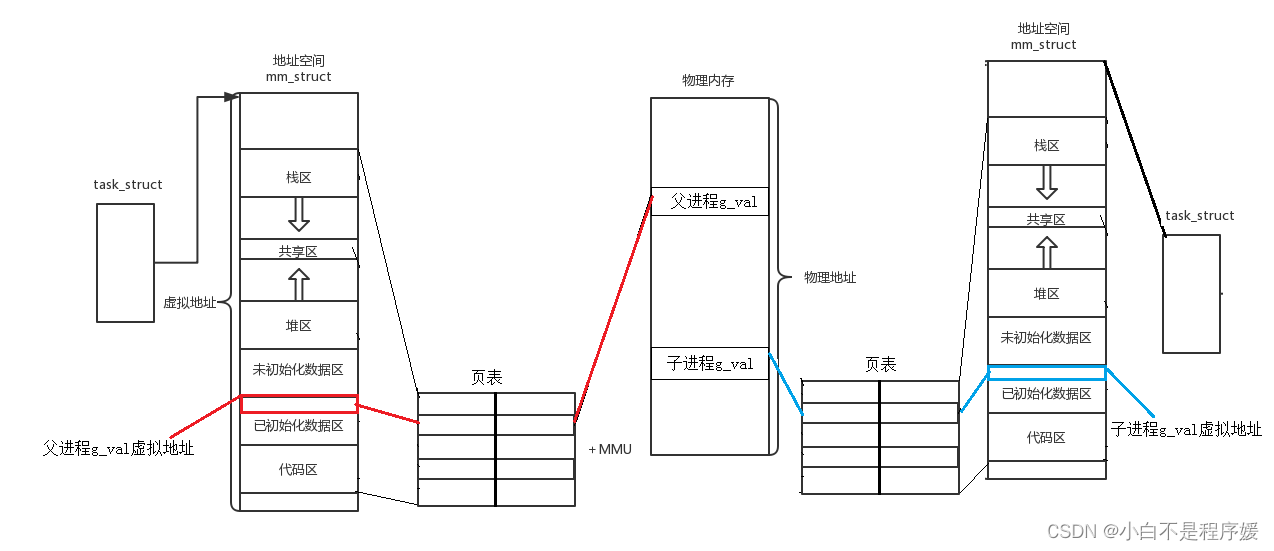
【Linux系统化学习】进程地址空间 | 虚拟地址和物理地址的关系
个人主页点击直达:小白不是程序媛 Linux专栏:Linux系统化学习 代码仓库:Gitee 目录 虚拟地址和物理地址 页表 进程地址空间 进程地址空间存在的意义 虚拟地址和物理地址 我们在学习C/C的时候肯定都见过下面这张有关于内存分布的图片&a…...
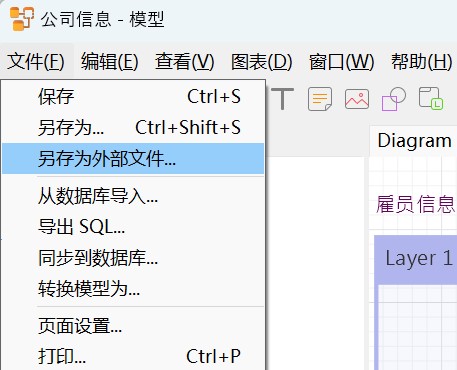
Navicat 技术指引 | 适用于 GaussDB 分布式的模型功能
Navicat Premium(16.3.3 Windows 版或以上)正式支持 GaussDB 分布式数据库。GaussDB 分布式模式更适合对系统可用性和数据处理能力要求较高的场景。Navicat 工具不仅提供可视化数据查看和编辑功能,还提供强大的高阶功能(如模型、结…...

四十五、Redis主从
目录 1、数据同步原理 (1)全量同步 (2)增量同步 (3)优化Redis主从集群 (4)什么时候执行全量同步 (5)什么时候执行增量同步 2、流程 1、数据同步原理 &…...

Spring源码学习一
IOC容器概述 ApplicationContext接口相当于负责bean的初始化、配置和组装的IoC容器. Spring为ApplicationContext提供了一些开箱即用的实现, 独立的应用可以使用 ClassPathXmlApplicationContext或者FileSystemXmlApplicationContext,web应用在web.xml配置监 听&am…...

小红书种草和抖音传播区别是什么?
目前品牌较为关注的2大平台小红书和抖音,两者在种草方面存在一些明显的区别。本次就存量竞争、种草形式和种草策略这三个方面入手进行分析,今天和大家分享下小红书种草和抖音传播区别是什么? 一、存量竞争下的2大平台 2个都是属于存量竞争下的…...

论文阅读《Parameterized Cost Volume for Stereo Matching》
论文地址:https://openaccess.thecvf.com/content/ICCV2023/papers/Zeng_Parameterized_Cost_Volume_for_Stereo_Matching_ICCV_2023_paper.pdf 源码地址:https://github.com/jiaxiZeng/Parameterized-Cost-Volume-for-Stereo-Matching 概述 现有的立体匹…...
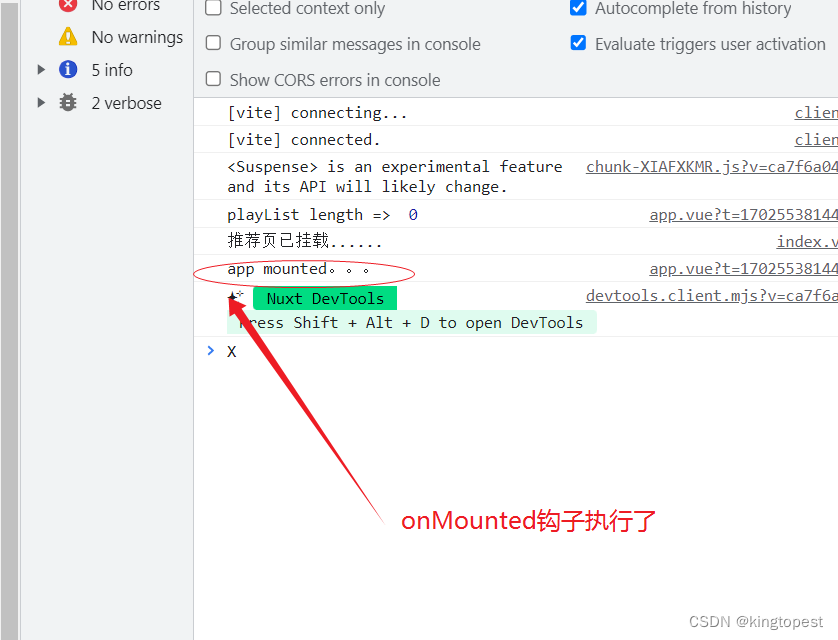
解决nuxt3中vue3生命周期钩子onMounted不执行的问题
看到这篇文章算你运气好!因为只有我才能给你答案!看到就赚到,这就是缘分 因为vue3迁移nuxt3是一个非常困难和痛苦的过程,中间会有各种报错,各种不兼容,各种乱七八糟但是你又找不到答案的问题。 而且你一定…...

Win32 HIWORD和LOWORD宏学习
HIWORD是High Word的缩写,作用是取得某个4字节变量(即32位的值)在内存中处于高位的两个字节,即一个word长的数据; LOWORD是Low Word的缩写,作用是取得某个4字节变量(即32位的值)在内存中处于低位的两个字节,即一个word长的数据; Win32编程常用; Win32窗口编程中,收到 WM_S…...

Axure官方软件安装、汉化保姆级教程(带官方资源下载)
1.下载汉化包 百度云链接:https://pan.baidu.com/s/1lluobjjBZvitASMt8e0A_w?pwdjqxn 提取码: jqxn 2.解压压缩包 3.安装Axure 进行安装 点击next 打勾,然后next, 默认是c盘,修改成自己的文件夹(不要什么都放c盘里…...

qt-C++笔记之addAction和addMenu的区别以及QAction的使用场景
qt-C笔记之addAction和addMenu的区别以及QAction的使用场景 code review! 文章目录 qt-C笔记之addAction和addMenu的区别以及QAction的使用场景1.QMenu和QMenuBar的关系与区别2.addMenu和addAction的使用场景区别3.将QAction的信号连接到槽函数4.QAction的使用场景5.将例1修改…...

nodejs 管道通讯
概述 2个nodejs程序的一种通讯方式,管道通讯,跟其他语言一样,管道通讯是一种特殊的socket通讯,普通的socket通讯是通过监听端口触发通讯机制,管道通讯是通过监听文件的方式进行通讯,一般用于单机的多进程通…...

k8s常用命令及示例(三):apply 、edit、delete
k8s常用命令及示例(三):apply 、edit、delete 1. kubectl apply -f 命令:从yaml文件中创建资源对象。 -f 参数为强制执行。kubectl apply和kubectl create的区别如下:kubectl create 和 kubectl apply 是 Kubernetes 中两个常用的命令&…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...

恶补电源:1.电桥
一、元器件的选择 搜索并选择电桥,再multisim中选择FWB,就有各种型号的电桥: 电桥是用来干嘛的呢? 它是一个由四个二极管搭成的“桥梁”形状的电路,用来把交流电(AC)变成直流电(DC)。…...

基于谷歌ADK的 智能产品推荐系统(2): 模块功能详解
在我的上一篇博客:基于谷歌ADK的 智能产品推荐系统(1): 功能简介-CSDN博客 中我们介绍了个性化购物 Agent 项目,该项目展示了一个强大的框架,旨在模拟和实现在线购物环境中的智能导购。它不仅仅是一个简单的聊天机器人,更是一个集…...

LeetCode 0386.字典序排数:细心总结条件
【LetMeFly】386.字典序排数:细心总结条件 力扣题目链接:https://leetcode.cn/problems/lexicographical-numbers/ 给你一个整数 n ,按字典序返回范围 [1, n] 内所有整数。 你必须设计一个时间复杂度为 O(n) 且使用 O(1) 额外空间的算法。…...
