【深度学习】强化学习(二)马尔可夫决策过程
文章目录
- 一、强化学习问题
- 1、交互的对象
- 2、强化学习的基本要素
- 3、策略(Policy)
- 4、马尔可夫决策过程
- 1. 基本元素
- 2. 交互过程的表示
- 3. 马尔可夫过程(Markov Process)
- 4. 马尔可夫决策过程(MDP)
- 5. 轨迹的概率计算
- 6. 给西瓜浇水问题的马尔可夫决策过程
一、强化学习问题
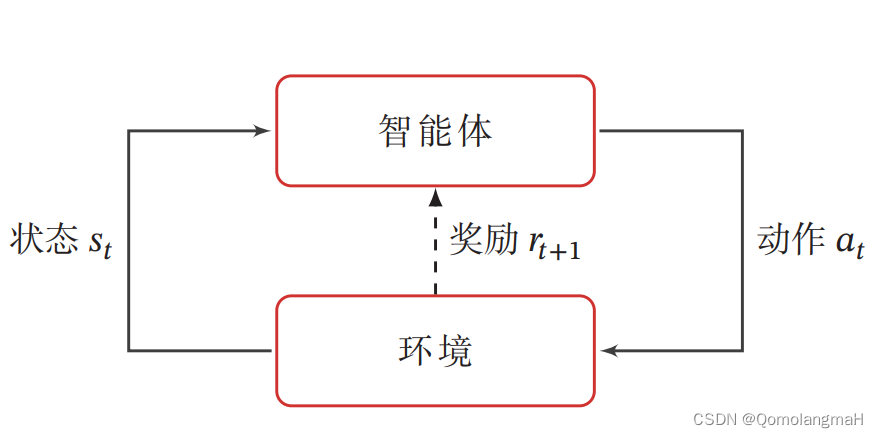
强化学习的基本任务是通过智能体与环境的交互学习一个策略,使得智能体能够在不同的状态下做出最优的动作,以最大化累积奖励。这种学习过程涉及到智能体根据当前状态选择动作,环境根据智能体的动作转移状态,并提供即时奖励的循环过程。
1、交互的对象
在强化学习中,有两个可以进行交互的对象:智能体和环境
-
智能体(Agent):能感知外部环境的状态(State)和获得的奖励(Reward),并做出决策(Action)。智能体的决策和学习功能使其能够根据状态选择不同的动作,学习通过获得的奖励来调整策略。
-
环境(Environment):是智能体外部的所有事物,对智能体的动作做出响应,改变状态,并反馈相应的奖励。
2、强化学习的基本要素
强化学习涉及到智能体与环境的交互,其基本要素包括状态、动作、策略、状态转移概率和即时奖励。
-
状态(State):对环境的描述,可能是离散或连续的。
-
动作(Action):智能体的行为,也可以是离散或连续的。
-
策略(Policy):智能体根据当前状态选择动作的概率分布。
-
状态转移概率(State Transition Probability):在给定状态和动作的情况下,环境转移到下一个状态的概率。
-
即时奖励(Immediate Reward):智能体在执行动作后,环境反馈的奖励。
3、策略(Policy)
策略(Policy)就是智能体如何根据环境状态 𝑠 来决定下一步的动作 𝑎(智能体在特定状态下选择动作的规则或分布)。
- 确定性策略(Deterministic Policy) 直接指定智能体应该采取的具体动作
- 随机性策略(Stochastic Policy) 则考虑了动作的概率分布,增加了对不同动作的探索。
上述概念可详细参照:【深度学习】强化学习(一)强化学习定义
4、马尔可夫决策过程
为了简化描述,将智能体与环境的交互看作离散的时间序列。智能体从感知到的初始环境 s 0 s_0 s0 开始,然后决定做一个相应的动作 a 0 a_0 a0,环境相应地发生改变到新的状态 s 1 s_1 s1,并反馈给智能体一个即时奖励 r 1 r_1 r1,然后智能体又根据状态 s 1 s_1 s1做一个动作 a 1 a_1 a1,环境相应改变为 s 2 s_2 s2,并反馈奖励 r 2 r_2 r2。这样的交互可以一直进行下去: s 0 , a 0 , s 1 , r 1 , a 1 , … , s t − 1 , r t − 1 , a t − 1 , s t , r t , … , s_0, a_0, s_1, r_1, a_1, \ldots, s_{t-1}, r_{t-1}, a_{t-1}, s_t, r_t, \ldots, s0,a0,s1,r1,a1,…,st−1,rt−1,at−1,st,rt,…,其中 r t = r ( s t − 1 , a t − 1 , s t ) r_t = r(s_{t-1}, a_{t-1}, s_t) rt=r(st−1,at−1,st) 是第 t t t 时刻的即时奖励。这个交互过程可以被视为一个马尔可夫决策过程(Markov Decision Process,MDP)。
1. 基本元素
-
状态( s t s_t st):
- 表示智能体与环境交互中的当前情况或环境状态。
- 在时间步𝑡时,智能体和环境的状态为 s t s_t st。
-
动作 ( a t a_t at):
- 表示智能体在给定状态 s t s_t st下采取的动作。
- 在时间步𝑡时,智能体选择执行动作 a t a_t at。
-
奖励 ( r t r_t rt):
- 表示在智能体采取动作 a t a_t at后,环境反馈给智能体的即时奖励。
- 在时间步𝑡时,智能体获得奖励 r t r_t rt。
2. 交互过程的表示
- 智能体与环境的交互过程可以用离散时间序列表示:
s 0 , a 0 , s 1 , r 1 , a 1 , … , s t − 1 , r t − 1 , a t − 1 , s t , r t , … , s_0, a_0, s_1, r_1, a_1, \ldots, s_{t-1}, r_{t-1}, a_{t-1}, s_t, r_t, \ldots, s0,a0,s1,r1,a1,…,st−1,rt−1,at−1,st,rt,…, - 在每个时间步,智能体根据当前状态选择一个动作,环境根据智能体的动作和当前状态发生转移,并反馈即时奖励。
- 这种时间序列描述强调了智能体和环境之间的交互,以及在时间步𝑡时智能体和环境的状态、动作和奖励。这符合马尔可夫决策过程的基本定义,其中马尔可夫性质要求当前状态包含了所有与未来预测相关的信息。
3. 马尔可夫过程(Markov Process)
-
定义: 马尔可夫过程是一组具有马尔可夫性质的随机变量序列 s 0 , s 1 , … , s t ∈ S s_0, s_1, \ldots, s_t \in \mathcal{S} s0,s1,…,st∈S,其中 S \mathcal{S} S 是状态空间。
-
马尔可夫性质: 当前状态 s t s_t st 对未来的预测只依赖于当前状态,而不依赖于过去的状态序列( s t − 1 , s t − 2 , … , s 0 s_{t-1}, s_{t-2}, \ldots, s_0 st−1,st−2,…,s0),即
p ( s t + 1 ∣ s t , … , s 0 ) = p ( s t + 1 ∣ s t ) p(s_{t+1} | s_t, \ldots, s_0) = p(s_{t+1} | s_t) p(st+1∣st,…,s0)=p(st+1∣st) -
状态转移概率 p ( s t + 1 ∣ s t ) p(s_{t+1} | s_t) p(st+1∣st): 表示在给定当前状态 s t s_t st 的条件下,下一个时刻的状态为 s t + 1 s_{t+1} st+1 的概率,满足 ∑ S t + 1 ∈ S p ( s t + 1 ∣ s t ) = 1 \sum_{S_{t+1} \in \mathcal{S}}p(s_{t+1} | s_t) = 1 ∑St+1∈Sp(st+1∣st)=1
4. 马尔可夫决策过程(MDP)
-
加入动作: MDP 在马尔可夫过程的基础上引入了动作变量 a t a_t at,表示智能体在状态 s t s_t st 时选择的动作。
-
状态转移概率的扩展: 在MDP中,下一个时刻的状态 s t + 1 s_{t+1} st+1 不仅依赖于当前状态 s t s_t st,还依赖于智能体选择的动作 a t a_t at:
p ( s t + 1 ∣ s t , a t , … , s 0 , a 0 ) = p ( s t + 1 ∣ s t , a t ) p(s_{t+1} | s_t,a_t, \ldots, s_0, a_0) =p(s_{t+1} | s_t, a_t) p(st+1∣st,at,…,s0,a0)=p(st+1∣st,at) -
马尔可夫决策过程的特点: 在MDP中,智能体的决策不仅受当前状态的影响,还受到智能体选择的动作的影响,从而更加适应需要制定决策的场景。
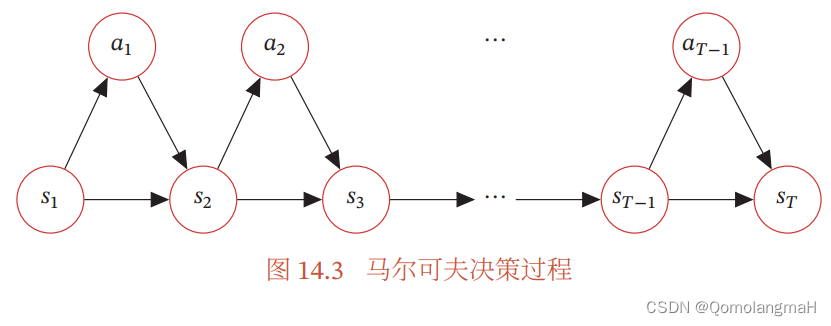
5. 轨迹的概率计算
-
轨迹表示: 给定策略 π ( a ∣ s ) \pi(a|s) π(a∣s),MDP的一个轨迹 τ \tau τ 表示智能体与环境交互的一系列状态、动作和奖励的序列:
τ = s 0 , a 0 , s 1 , r 1 , a 1 , … , s T − 1 , r T − 1 , a T − 1 , s T , r T , … , \tau=s_0, a_0, s_1, r_1, a_1, \ldots, s_{T-1}, r_{T-1}, a_{T-1}, s_T, r_T, \ldots, τ=s0,a0,s1,r1,a1,…,sT−1,rT−1,aT−1,sT,rT,…, -
概率计算公式:
p ( τ ) = p ( s 0 , a 0 , s 1 , r 1 , … ) p(\tau) = p(s_0, a_0, s_1, r_1, \ldots) p(τ)=p(s0,a0,s1,r1,…) p ( τ ) = p ( s 0 ) ∏ t = 0 T − 1 π ( a t ∣ s t ) p ( s t + 1 ∣ s t , a t ) p(\tau) = p(s_0) \prod_{t=0}^{T-1} \pi(a_t|s_t) p(s_{t+1}|s_t, a_t) p(τ)=p(s0)t=0∏T−1π(at∣st)p(st+1∣st,at)- p ( s 0 ) p(s_0) p(s0) 是初始状态的概率。
- π ( a t ∣ s t ) \pi(a_t|s_t) π(at∣st) 是策略:在状态 s t s_t st 下选择动作 a t a_t at 的概率。
- p ( s t + 1 ∣ s t , a t ) p(s_{t+1}|s_t, a_t) p(st+1∣st,at) 是在给定当前状态 s t s_t st 和动作 a t a_t at 的条件下,下一个时刻的状态为 s t + 1 s_{t+1} st+1 的概率(状态转移概率
)。
-
轨迹的联合概率:
- 通过对轨迹中每个时刻的概率连乘,得到整个轨迹的联合概率。
6. 给西瓜浇水问题的马尔可夫决策过程

在给西瓜浇水的马尔可夫决策过程中,只有四个状态(健康、缺水、溢水、凋亡)和两个动作(浇水、不浇水),在每一
步转移后,若状态是保持瓜苗健康则获得奖赏1 ,瓜苗缺水或溢水奖赏为- 1 , 这时通过浇水或不浇水可以恢复健康状态,当瓜苗凋亡时奖赏是最小值-100 且无法恢复。图中箭头表示状态转移,箭头旁的 a , p , r a,p,r a,p,r分别表示导致状态转移的动作、转移概率以及返回的奖赏.容易看出,最优策略在“健康”状态选择动作 “浇水”、在 “溢水”状态选择动作“不浇水”、在 “缺水”状态选择动作 “浇水”、在 “凋亡”状态可选择任意动作。
相关文章:

【深度学习】强化学习(二)马尔可夫决策过程
文章目录 一、强化学习问题1、交互的对象2、强化学习的基本要素3、策略(Policy)4、马尔可夫决策过程1. 基本元素2. 交互过程的表示3. 马尔可夫过程(Markov Process)4. 马尔可夫决策过程(MDP)5. 轨迹的概率计…...

Vue.js 使用基础知识
Vue.js 是一款用于构建用户界面的渐进式框架,它专注于视图层。Vue.js 不同于传统的 JavaScript 框架,它采用了组件化的开发方式,使得开发者可以更加高效和灵活地构建交互式的 Web 应用程序。 目录 什么是 Vue.js安装 Vue.jsVue 实例模板语法插…...

Linux---计划任务
本章主要介绍如何创建计划任务 使用 at 创建计划任务使用 crontab 创建计划任务 有时需要在某个指定的时间执行一个操作,此时就要使用计划任务了。计划任务有两种: 一个是at计划任务,另一个是 crontab计划任务。 下面我们分别来看这两种计划…...

.NET微信网页开发之通过UnionID机制解决多应用用户帐号统一问题
背景 随着公司微信相关业务场景的不断拓展,从最初的一个微信移动应用、然后发展成微信公众号应用、然后又有了微信小程序应用。但是随着应用的拓展,如何保证相同用户的微信用户在不同应用中登录的同一个账号呢?今天的主题就来了.NET微信网页…...
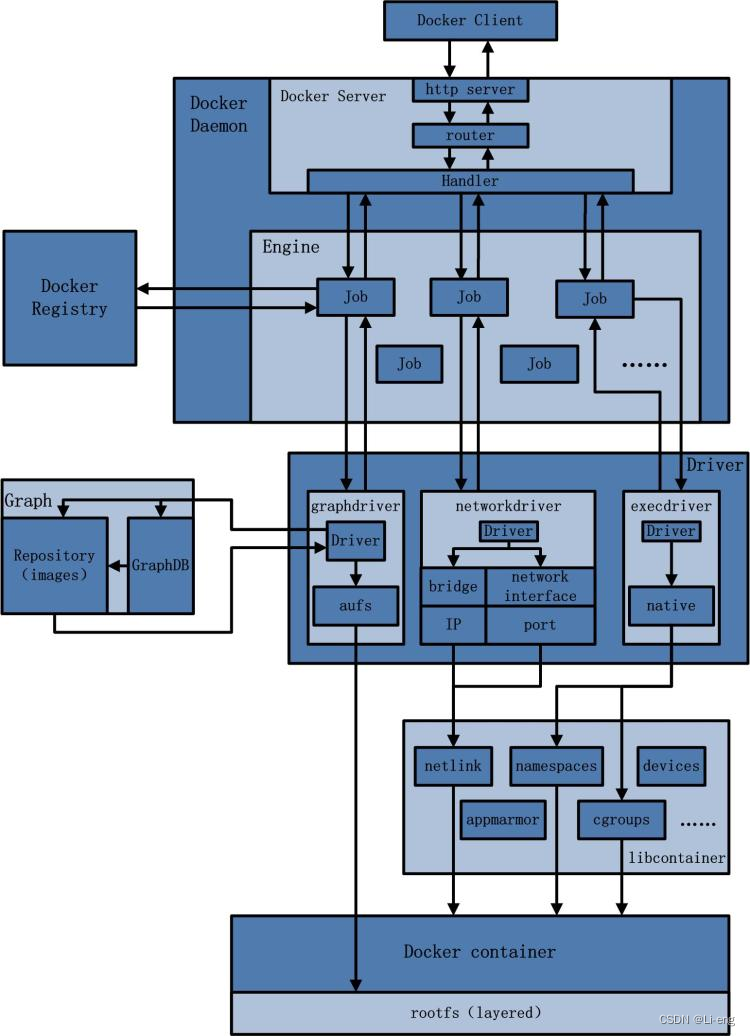
【docker】docker入门与安装
Docker 一、入门 Docker的主要目标是:Build, Ship and Run Any App, Anywhere,也就是通过对应用组件的封装、分发、部署、运行等生命周期的管理,使用户的APP及其运行环境能做到一次镜像,处处运行。 Docker运行速度快的原因 Docker有比虚拟…...
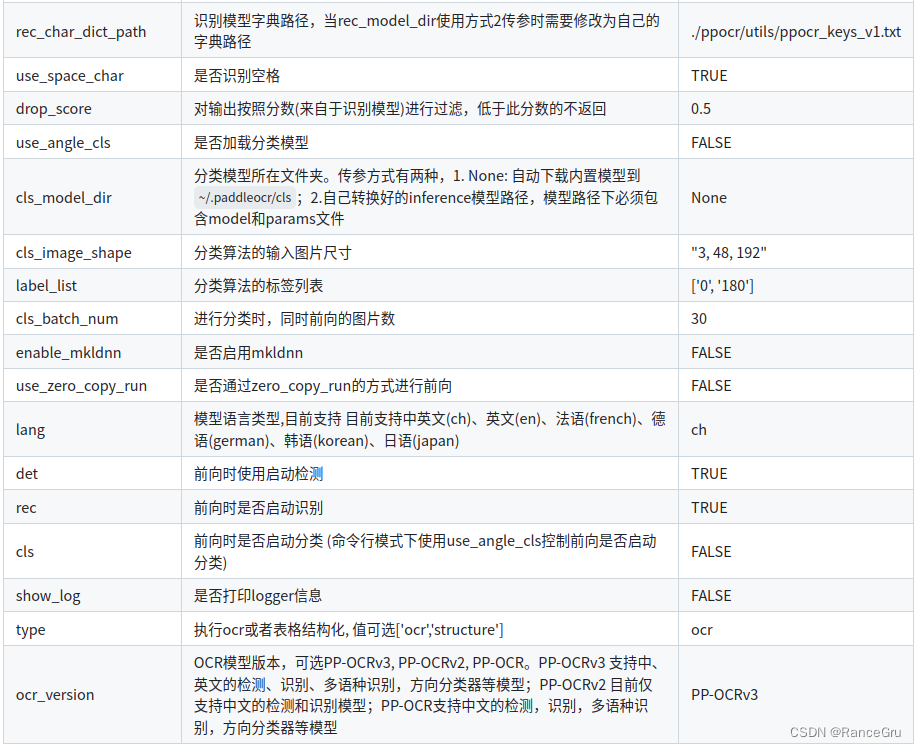
视觉学习笔记12——百度飞浆框架的PaddleOCR 安装、标注、训练以及测试
系列文章目录 虚拟环境部署 参考博客1 参考博客2 参考博客3 参考博客4 文章目录 系列文章目录一、简单介绍1.OCR介绍2.PaddleOCR介绍 二、安装1.anaconda基础环境1)anaconda的基本操作2)搭建飞浆的基础环境 2.安装paddlepaddle-gpu版本1)安装…...

深入分析ClassLocader工作机制
文章目录 一、ClassLoader简介1. 概念2. ClassLoader类结构分析 二、ClassLoader的双亲委派机制三、Class文件的加载流程1. 简介2. 加载字节码到内存3. 验证与解析4. 初始化Class对象 四、常见加载类错误分析1. ClassNotFoundException2. NoClassDefFoundError3. UnsatisfiledL…...
算法通关村第十二关—字符串转换(青铜)
一、转换成小写字母 LeetCode709.给你一个字符串s,将该字符串中的大写字母转换成相同的小写字母,返回新的字符串。 示例1: 输入:s"Hello" 输出:"hello" 示例2: 输入:s&qu…...
)
C#基础与进阶扩展合集-基础篇(持续更新)
目录 本文分两篇,进阶篇点击:C#基础与进阶扩展合集-进阶篇 一、基础入门 Ⅰ 关键字 Ⅱ 特性 Ⅲ 常见异常 Ⅳ 基础扩展 1、哈希表 2、扩展方法 3、自定义集合与索引器 4、迭代器与分部类 5、yield return 6、注册表 7、不安全代码 8、方法…...

ReactJs笔记摘录
文章目录 前言目录结构组件动态组件高阶组件 Hook函数useStateuseEffectuseContextuseReduceruseCallbackuseMemo JSX语法根元素与斜杠使用变量推荐使用className替代class属性写法三元表达式 vs &&antd和tailwindcss 组件通信父传子:props和自定义函数事件…...

2023 re:Invent使用 PartyRock 和 Amazon Bedrock 安全高效构建 AI 应用程序
前言 本篇文章授权活动官方亚马逊云科技文章转发、改写权,包括不限于在 亚马逊云科技开发者社区, 知乎,自媒体平台,第三方开发者媒体等亚马逊云科技官方渠道 “Your Data, Your AI, Your Future.(你的数据,你的AI&…...

Mac 打不开github解决方案
序言 github 时有打不开的情况,为此很是烦恼,这里分享一下如何解决这种问题,其实问题的本质是在访问github网页时无法通过github.com的二级域名进行动态域名解析。 解决方案 手动配置静态文件hosts,将该域名和IP的映射关系添加…...

十五 动手学深度学习v2计算机视觉 ——全连接神经网络FCN
文章目录 FCN FCN 全卷积网络先使用卷积神经网络抽取图像特征,然后通过卷积层将通道数变换为类别个数,最后通过转置卷积层将特征图的高和宽变换为输入图像的尺寸。 因此,模型输出与输入图像的高和宽相同,且最终输出通道包含了该空…...
elementUI中的 “this.$confirm“ 基本用法,“this.$confirm“ 调换 “确认“、“取消“ 按钮的位置
文章目录 前言具体操作总结 前言 elementUI中的 "this.$confirm" 基本用法,"this.$confirm" 调换 "确认"、"取消" 按钮的位置 具体操作 基本用法 <script> this.$confirm(这是数据(res.data࿰…...

K8S 常用命令
获取所有的pod资源: kubectl get pod 获取所有的命名空间: kubectl get namespace 获取所有的Deployment资源: kubectl get deployment 删除指定的deploy: kubectl delete deploy nginx 获取所有的服务: kubectl get serv…...

12.使用 Redis 优化登陆模块
目录 1. 使用 Redis 优化登陆模块 1.1 使用 Redis 存储验证码 1.2 使用 Redis 存储登录凭证 1.3 使用 Redis 缓存用户信息 1. 使用 Redis 优化登陆模块 使用 Redis 存储验证码:验证码需要频繁的访问与刷新,对性能要求较高;验证码不需要永…...
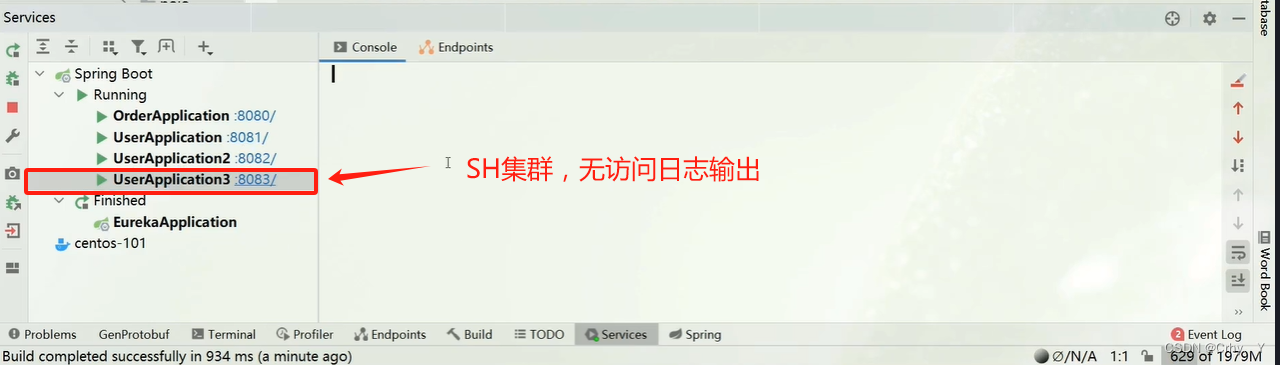
Nacos-NacosRule 负载均衡—设置集群使本地服务优先访问
userservice: ribbon: NFLoadBalancerRuleClassName: com.alibaba.cloud.nacos.ribbon.NacosRule # 负载均衡规则 NacosRule 权重计算方法 目录 一、介绍 二、示例(案例截图) 三、总结 一、介绍 NacosRule是AlibabaNacos自己实现的一个负载均衡策略&…...
软件设计师——信息安全(二)
📑前言 本文主要是【信息安全】——软件设计师——信息安全的文章,如果有什么需要改进的地方还请大佬指出⛺️ 🎬作者简介:大家好,我是听风与他🥇 ☁️博客首页:CSDN主页听风与他 🌄…...

Unity中实现ShaderToy卡通火(原理实现篇)
文章目录 前言一、我们在片元着色器中,实现卡通火的大体框架1、使用 noise 和 _CUTOFF 判断作为显示火焰的区域2、_CUTOFF : 用于裁剪噪波范围的三角形3、noise getNoise(uv, t); : 噪波函数 二、顺着大体框架依次解析具体实现的功能1、 uv.x * 4.0; : …...
引迈信息-JNPF平台怎么样?值得入手吗?
目录 1.前言 2.引迈低代码怎么样? 3.平台亮点展示 4.引迈产品特点 5.引迈产品技术栈: 1.前言 低代码是近几年比较火的一种应用程序快速开发方式,它能帮助用户在开发软件的过程中大幅减少手工编码量,并通过可视化组件加速应用…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...