计算机网络:物理层(编码与调制)
今天又学会了一个知识,加油!
目录
一、基带信号与宽带信号
1、基带信号
2、宽带信号
3、选择
4、关系
二、数字数据编码为数字信号
1、非归零编码【NRZ】
2、曼彻斯特编码
3、差分曼彻斯特编码
4、归零编码【RZ】
5、反向不归零编码【NRZI】
6、4B/5B编码(了解)
三、数字数据调制为模拟信号
总结
一、基带信号与宽带信号
信道:信号的传输媒介。一般用来表示向某一个方向传送信息的介质,因此一条通信线路往往包含一条发送信道和一条接收信道。
1、基带信号
将数字信号1和o直接用两种不同的电压表示,再送到数字信道上去传输(基带传输)。来自信源的信号,像计算机输出的代表各种文字或图像文件的数据信号都属于基带信号。基带信号就是发出的直接表达了要传输的信息的信号,比如我们说话的声波就是基带信号。
2、宽带信号
将基带信号进行调制后形成的频分复用模拟信号,再传送到模拟信道上去传输(宽带传输)。把基带信号经过载波调制后,把信号的频率范围搬移到较高的频段以便在信道中传输(即仅在一段频率范围内能够通过信道)。
3、选择
在传输距离较近时,计算机网络采用基带传输方式(近距离衰减小,从而信号内容不易发生变化)
在传输距离较远时,计算机网络采用宽带传输方式(远距离衰减大,即使信号变化大也能最后过滤出来基带信号)
4、关系

二、数字数据编码为数字信号
1、非归零编码【NRZ】
高1低0
编码容易实现,但没有检错功能,且无法判断一个码元的开始和结束,以至于收发双方难以保持同步。
2、曼彻斯特编码
解释:将一个码元分成两个相等的间隔,前一个间隔为低电平后一个间隔为高电平表示码元1;码元0则正好相反。也可以采用相反的规定。该编码的特点是在每一个码元的中间出现电平跳变,位中间的跳变既作时钟信号(可用于同步),又作数据信号,但它所占的频带宽度是原始的基带宽度的两倍。每一个码元都被调成两个电平,所以数据传输速率只有调制速率的1/2。

3、差分曼彻斯特编码
同1异0(以虚线区分)
常用于局域网传输,其规则是:若码元为1,则前半个码元的电平与上一个码元的后半个码元的电平相同,若为0,则相反。该编码的特点是,在每个码元的中间,都有一次电平的跳转,可以实现自同步,且抗干扰性强于曼彻斯特编码。
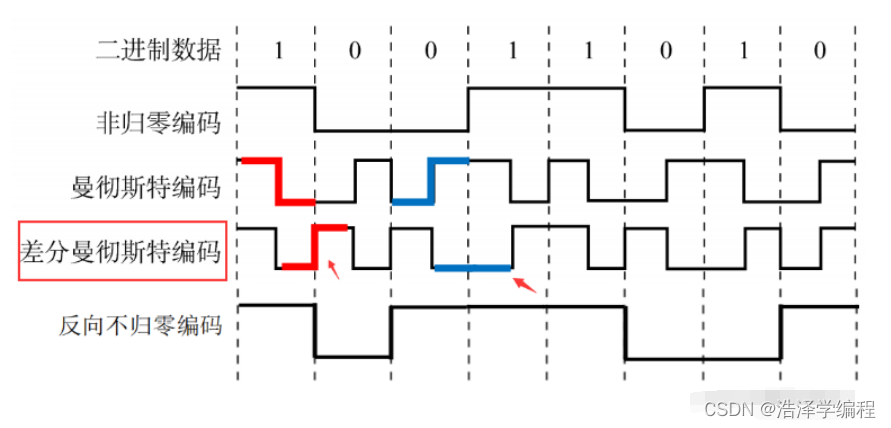
此时总结一下:遇0跳变,遇1不变。
4、归零编码【RZ】
信号电平在一个码元之内都要恢复到零的这种编码成编码方式。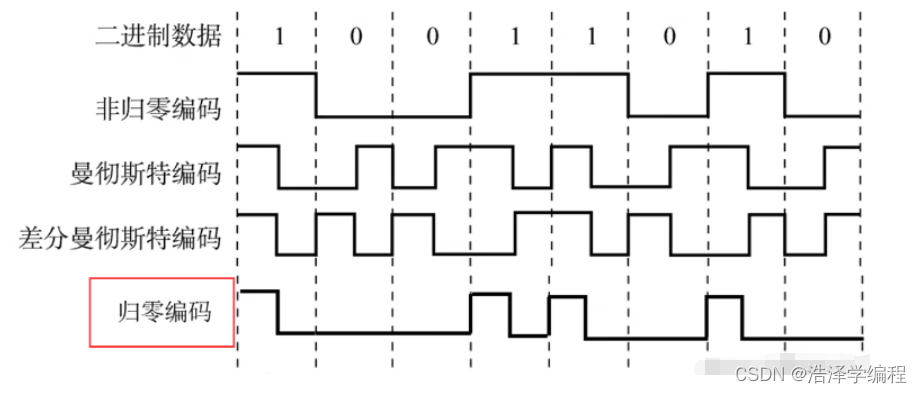
5、反向不归零编码【NRZI】
信号电平翻转表示0,信号电平不变表示1。

6、4B/5B编码(了解)
比特流中插入额外的比特以打破一连串的0或1,就是用5个比特来编码4个比特的数据,之后再传给接收方,因此称为4B/5B。编码效率为80%。
只采用16种对应16种不同的4位码,其他的16种作为控制码(帧的开始和结束,线路的状态信息等)或保留。

三、数字数据调制为模拟信号
数字数据调制技术在发送端将数字信号转换为模拟信号,而在接收端将模拟信号还原为数字信号,分别对应于调制解调器的调制和解调过程。
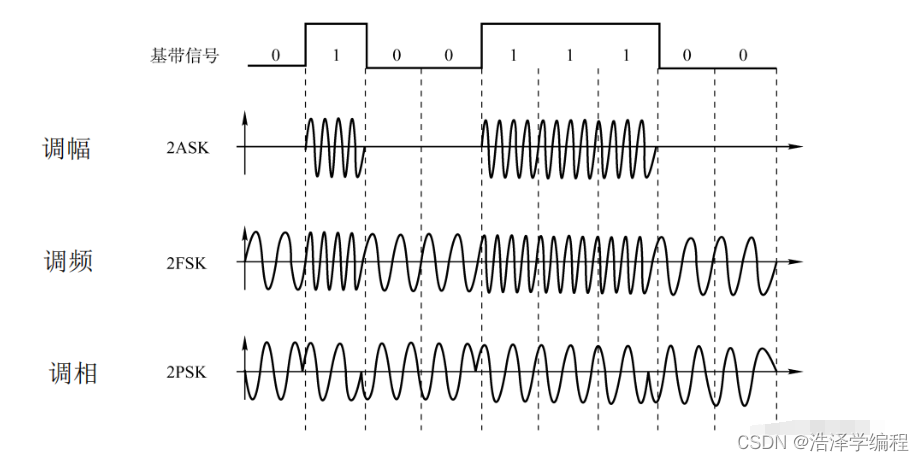
调幅+调相(QAM)
某通信链路的波特率是1200Baud,采用4个相位,每个相位有4种振幅的QAM调制技术,则该链路的信息传输速率是多少?
解答:
四个相位,四种振幅,所以有44=16种码元。
log_2 16=4bit(1码元)
所以该链路的信息传输速率是12004=4800b/s。
总结
以上就是物理层之编码与调制(非归零编码、慢车斯顿编码、差分曼彻斯特编码、归零编码、反向不归零编码、4B/5B编码)的相关知识点,希望对你有所帮助。
相关文章:

计算机网络:物理层(编码与调制)
今天又学会了一个知识,加油! 目录 一、基带信号与宽带信号 1、基带信号 2、宽带信号 3、选择 4、关系 二、数字数据编码为数字信号 1、非归零编码【NRZ】 2、曼彻斯特编码 3、差分曼彻斯特编码 4、归零编码【RZ】 5、反向不归零编码【NRZI】 …...
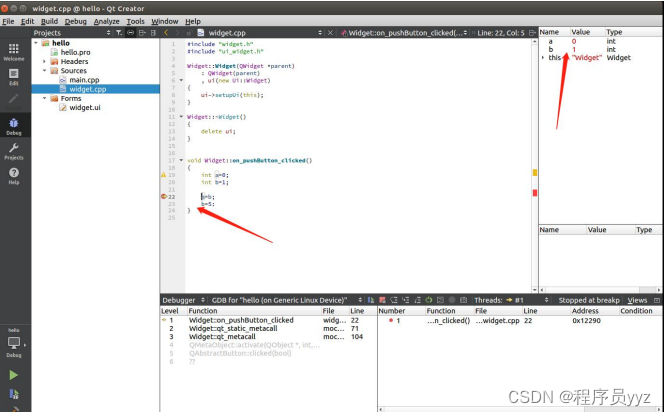
嵌入式开发板qt gdb调试
1) 启动 gdbserver ssh 或者 telnet 登陆扬创平板 192.168.0.253, 进入命令行执行如下: chmod 777 /home/HelloWorld (2) 打 开 QTcreator->Debug->StartDebugging->Attach to Running Debug Server 进行…...

基于python实现原神那维莱特开转脚本
相信不少原友都抽取了枫丹大C那维莱特,其强力的输出让不少玩家爱不释手。由于其转的越快,越不容易丢伤害的特点,很多原友在开转时容易汗流浃背,所以特意用python写了一个自动转圈脚本,当按住鼠标侧键时,即可…...

C# 实现Lru缓存
C# 实现Lru缓存 LRU 算法全称是最近最少使用算法(Least Recently Use),是一种简单的缓存策略。 通常用在对象池等需要频繁获取但是又需要释放不用的地方。 代码实现的基本原理就是使用链表,当某个元素被访问时(Get或…...
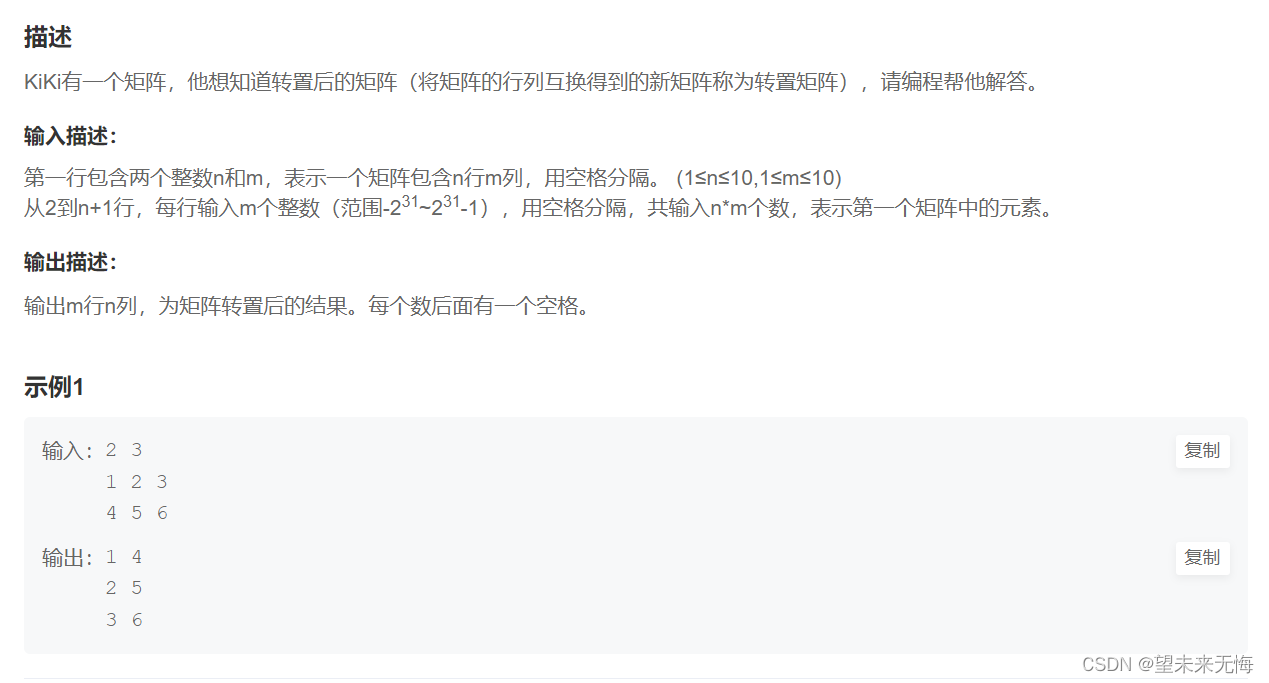
牛客网BC107矩阵转置
答案: #include <stdio.h> int main() {int n0, m0,i0,j0,a0,b0;int arr1[10][10]{0},arr2[10][10]{0}; //第一个数组用来储存原矩阵,第二个数组用来储存转置矩阵scanf("%d%d",&n,&m); if((n>1&&n<10)&&am…...

协作办公原来如此简单?详解 ONLYOFFICE 协作空间 2.0 更新
协作办公原来如此简单?详解 ONLYOFFICE 协作空间 2.0 更新 上周,ONLYOFFICE 的协作空间推出升级版 2.0 版本了: ONLYOFFICE 协作空间 2.0 现已发布:新增公共房间、插件、重新分配数据、RTL 界面等功能 ONLYOFFICE 协作空间是去…...

2023年国赛高教杯数学建模A题定日镜场的优化设计解题全过程文档及程序
2023年国赛高教杯数学建模 A题 定日镜场的优化设计 原题再现 构建以新能源为主体的新型电力系统,是我国实现“碳达峰”“碳中和”目标的一项重要措施。塔式太阳能光热发电是一种低碳环保的新型清洁能源技术[1]。 定日镜是塔式太阳能光热发电站(以下…...
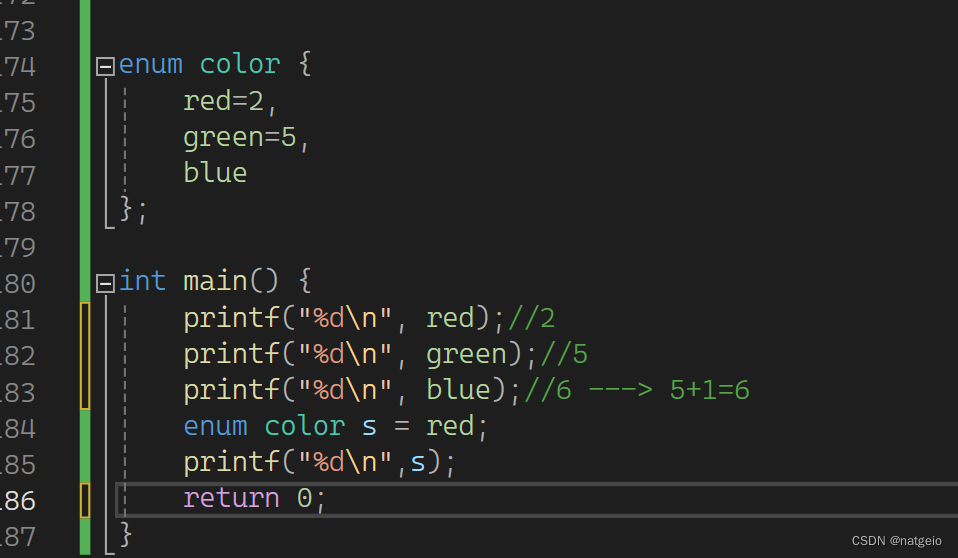
c/c++ 结构体、联合体、枚举
结构体 结构体内存对齐规则: 1、结构体的第一个成员对齐到结构体变量起始位置偏移量为0的地址处 2、其他成员变量要对齐到某个数字(对齐数)的整数倍的地址处。 对齐数:编译器默认的一个对齐数与该成员变量大小的较小值。 vs 中…...

stl模板库成员函数重载类型混肴编译不通过解决方法
stl模板库成员函数重载类型混肴编译不通过解决方法 这种方式编译不通过IsArithmetic和HasMemberList编译器存在混肴 template <typename T, typename Enable std::enable_if<IsArithmetic<T>::value>::type >static void DumpWrapper(T* filed, std::strin…...
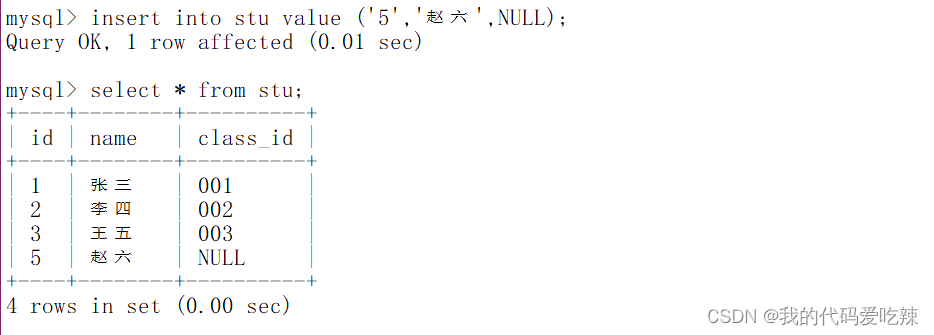
MySQL——表的约束
目录 一.表的约束 二.空属性 编辑三.默认值 四.列描述 五.主键 1.主键 2.符合主键 六.自增长 七.唯一键 八.外键 一.表的约束 真正约束字段的是数据类型,但是数据类型约束很单一,需要有一些额外的约束,更好的保证数据的合法性&…...
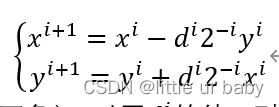
cordic 算法学习记录
参考:b站教学视频FPGA:Cordic算法介绍与实现_哔哩哔哩_bilibili FPGA硬件实现加减法、移位等操作比较简单,但是实现乘除以及函数计算复杂度高且占用资源多,常见的计算三角函数/平方根的求解方式有①查找表:先把函数对应…...

【STM32】电机驱动
一、电机分类 二、直流电机的分类 1.有刷电机 2.无刷电机 3.直流减速电机 三、H桥电路 正向旋转 驱动Q1和Q4 反向旋转 驱动Q2和Q3 四、MC3386电机驱动芯片 1.基本原理图 1)前进/后退:IN1和IN2的电平顺序决定电机的正反转 2)调节速度&#…...
)
csp 如此编码 C语言(回归唠嗑版)
熟悉的开篇废话,最近其实在研究那个web开发这一块,导致csp联系就减少了,好久没更csp的帖子了,尽管明天就要考了,但是嘞,能看一道是一道呗对吧。 等过段时间我把web开发这一块整明白了就发帖子,…...

或许是全网最全的延迟队列
什么是延迟队列 作用:用来存储延迟消息延迟消息:生产者发送一个消息给mq,然后mq会经过一段时间(延迟时间),然后在把这个消息发送给消费者 应用场景 预定会议后,需要在预定的时间点前十分钟通…...

C语言结构体小项目之通讯录代码实现+代码分析
一、思路 1.文件 这里由于通讯录实现代码较长,因此分三个文件进行,contact.c用于实现通讯录主体代码,声明各项头文件用contact.h实现,测试用test.c 二.功能 增加联系人删除联系人修改联系人查找指定联系人排序显示通讯录的信息…...
tp5 rewrite nginx重写
tp框架,默认的访问路径是 www.xxxx.com/index.php/admin/shop/index格式的,为了方便和更规范,也看起来有逼格一些,需要将index.php去掉 无index.php就会报404 我这里是宝塔 #地址重写if (!-e $request_filename) {rewrite ^(.*)$ /index.…...

.NET 反射优化的经验分享
比如针对 GetCustomAttributes 通过反射获取属性的优化,以下例子 // dotnet run -c Release -f net7.0 --filter "*" --runtimes net7.0 net8.0public class Tests{public object[] GetCustomAttributes() => typeof(C).GetCustomAttributes(typeof(MyAttribute…...

使用opencv的Sobel算子实现图像边缘检测
1 边缘检测介绍 图像边缘检测技术是图像处理和计算机视觉等领域最基本的问题,也是经典的技术难题之一。如何快速、精确地提取图像边缘信息,一直是国内外的研究热点,同时边缘的检测也是图像处理中的一个难题。早期的经典算法包括边缘算子方法…...

亿欧网首届“元创·灵镜”科技艺术节精彩纷呈,实在智能AI Agent智能体展现硬核科技图景
12月4日-10日,持续一周的首届“元创灵镜”科技艺术节在海南陵水香水湾拉开帷幕,虚实交互创造出的“海岛之镜”开幕式呈现出既真实又虚幻的未来感,融入前沿科技元素的艺术装置作品在“虚实之镜&自然生长”科技艺术展诠释着浪漫想象&#x…...
宝塔面板快速搭建本地网站结合内网穿透实现远程访问【无需公网IP】
文章目录 前言1. 环境安装2. 安装cpolar内网穿透3. 内网穿透4. 固定http地址5. 配置二级子域名6. 创建一个测试页面 前言 宝塔面板作为简单好用的服务器运维管理面板,它支持Linux/Windows系统,我们可用它来一键配置LAMP/LNMP环境、网站、数据库、FTP等&…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...
)
LLaMA-Factory 微调 Qwen2-VL 进行人脸情感识别(二)
在上一篇文章中,我们详细介绍了如何使用LLaMA-Factory框架对Qwen2-VL大模型进行微调,以实现人脸情感识别的功能。本篇文章将聚焦于微调完成后,如何调用这个模型进行人脸情感识别的具体代码实现,包括详细的步骤和注释。 模型调用步骤 环境准备:确保安装了必要的Python库。…...

GraphQL 实战篇:Apollo Client 配置与缓存
GraphQL 实战篇:Apollo Client 配置与缓存 上一篇:GraphQL 入门篇:基础查询语法 依旧和上一篇的笔记一样,主实操,没啥过多的细节讲解,代码具体在: https://github.com/GoldenaArcher/graphql…...
