矩阵理论及其应用邱启荣习题3.5题解
(1) P= ( − 1 0 1 − 1 − 1 2 1 1 − 1 ) \begin{pmatrix} -1 & 0&1 \\ -1 & -1&2\\1&1&-1 \end{pmatrix} −1−110−1112−1
A= ( 1 0 1 1 1 0 − 1 2 1 ) \begin{pmatrix} 1 & 0&1 \\ 1 & 1&0\\-1&2&1 \end{pmatrix} 11−1012101
B=P − 1 ^{-1} −1AP= ( − 2 − 3 5 0 0 2 − 2 − 2 5 ) \begin{pmatrix} -2 & -3&5 \\ 0 & 0&2\\-2&-2&5 \end{pmatrix} −20−2−30−2525
( 2 ) T ( α ) = T ( α 1 ) + 6 T ( α 2 ) − T ( α 3 ) = ( 1 , 0 , 1 ) + ( 6 , 6 , 0 ) + ( 1 , − 2 , − 1 ) = ( 8 , 4 , 0 ) \begin{aligned}(2)\space T(\alpha)&=T(\alpha_1)+6T(\alpha_2)-T(\alpha_3)\\&=(1,0,1)+(6,6,0)+(1,-2,-1)\\&=(8,4,0) \end{aligned} (2) T(α)=T(α1)+6T(α2)−T(α3)=(1,0,1)+(6,6,0)+(1,−2,−1)=(8,4,0)
T ( β ) = T ( e 1 ) − T ( e 2 ) + T ( e 3 ) = ( − 2 , − 3 , 5 ) + ( 0 , 0 , − 2 ) + ( − 2 , − 2 , 5 ) = ( − 4 , − 5 , 8 ) \begin{aligned}T(\beta)&=T(e_1)-T(e_2)+T(e_3)\\&=(-2,-3,5)+(0,0,-2)+(-2,-2,5)\\&=(-4,-5,8) \end{aligned} T(β)=T(e1)−T(e2)+T(e3)=(−2,−3,5)+(0,0,−2)+(−2,−2,5)=(−4,−5,8)
注意 α \alpha α是行向量
相关文章：
矩阵理论及其应用邱启荣习题3.5题解
(1) P ( − 1 0 1 − 1 − 1 2 1 1 − 1 ) \begin{pmatrix} -1 & 0&1 \\ -1 & -1&2\\1&1&-1 \end{pmatrix} −1−110−1112−1 A ( 1 0 1 1 1 0 − 1 2 1 ) \begin{pmatrix} 1 & 0&1 \\ 1 & 1&0\\-1&2&1 \end{pmat…...
Java面试题（每天10题）-------连载（49）
目录 Tomcat篇 1、Tomcat的缺省端口是多少？怎么修改？ 2、Tomcat有哪几种Connector运行模式（优化）？ 3、Tomcat有几种部署方式？ 4、Tomcat容器时如何创建servlet类实例？用到了什么原理&…...
python——数据类型
数据类型目录 前言一、Number（数字）数字类型转换：二、String（字符串）常用字符串运算符：字符串格式化：三、Tuple（元组）常用运算符四、List（列表）嵌套列表：常用列表操作：五、Dictionary（字典）六、Set（集合）...
hive中如何求取中位数？
目录 中位数的概念代码实现准备数据实现 中位数的概念 中位数（Median）又称中值，统计学中的专有名词，是按顺序排列的一组数据中居于中间位置的数，代表一个样本、种群或概率分布中的一个数值，其可将数值集合…...
在C#中异步编程
在C#中，异步编程是一种编写并发和响应式代码的技术，通过将耗时的操作放在后台线程中执行，以避免阻塞主线程，提高程序的性能和响应性。异步编程使用async和await关键字，结合任务（Task）和异步操作…...
微服务保护--Feign整合Sentinel
限流是一种预防措施，虽然限流可以尽量避免因高并发而引起的服务故障，但服务还会因为其它原因而故障。而要将这些故障控制在一定范围，避免雪崩，就要靠线程隔离（舱壁模式）和熔断降级手段了。 线程隔离之前讲到…...
二进制to十六进制
输入小于等于十六位的二进制数据，输出十六进制数据； #include <stdio.h> #include <stdlib.h> #include <math.h>int main(void) {char arr[16] { 0 }; int array[16] { 0 }; int hex[4] { 0 };int i 0; int num 0;scanf("…...
Logistic 回归算法
Logistic 回归 Logistic 回归算法Logistic 回归简述Sigmoid 函数Logistic 回归模型表达式求解参数 $\theta $梯度上升优化算法 Logistic 回归简单实现使用 sklearn 构建 Logistic 回归分类器Logistic 回归算法的优缺点 Logistic 回归算法 Logistic 回归简述 Logistic 回归是一…...
ubuntu安装详细步骤
一，先下载vmware 1，第一步打开上面链接 下载网址 : https://www.vmware.com/products/workstation-pro/wo rkstation-pro-evaluation.html 许可证 JU090-6039P-08409-8J0QH-2YR7F ZF3R0-FHED2-M80TY-8QYGC-NPKYF FC7D0-D1YDL-M8DXZ-CYPZE-P2AY6 ZC3T…...
力扣5. 最长回文子串
动态规划 思路： 假设 dp[i][j] 为字符串 (i, j) 子串是否为回文的结果；那么 dp[i][j] dp[i 1][j - 1] 且 (s[i] s[j])；长度为1的字符串都是回文； 原字符串长度为1，是回文；原字符串子串长度为1ÿ…...
肆[4]，函数VectorToHomMat2d/AffineTransPoint2d
函数VectorToHomMat2d C形式 LIntExport void VectorToHomMat2d( const HTuple& Px, const HTuple& Py, const HTuple& Qx, const HTuple& Qy, HTuple* HomMat2D);//参数1:图像坐标X数组 //参数2:图像坐标Y数组 //参数3:世界坐标X数组 //参数4:世界坐标Y…...
下载文件 后端返回给前端 response header 响应头
当浏览器在请求资源时，会通过http返回头中的content-type决定如何显示/处理将要加载的数据，如果这个类型浏览器能够支持阅览，浏览器就会直接展示该资源，比如png、jpeg、video等格式。在某些下载文件的场景中，服务端可能…...
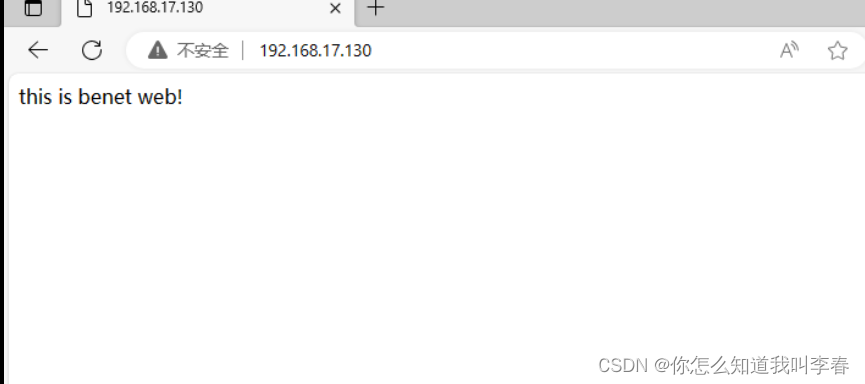
lvs负载均集群
目录 NAT模式 LVS负载均衡群集部署 1.部署共享存储 2.配置节点服务器 192.168.17.130 编辑 192.168.17.133 3.配置负载调度器 4.测试效果 NAT模式 LVS负载均衡群集部署 负载调度器：内网关 ens33：192.168.17.70，外网关 ens36&#x…...
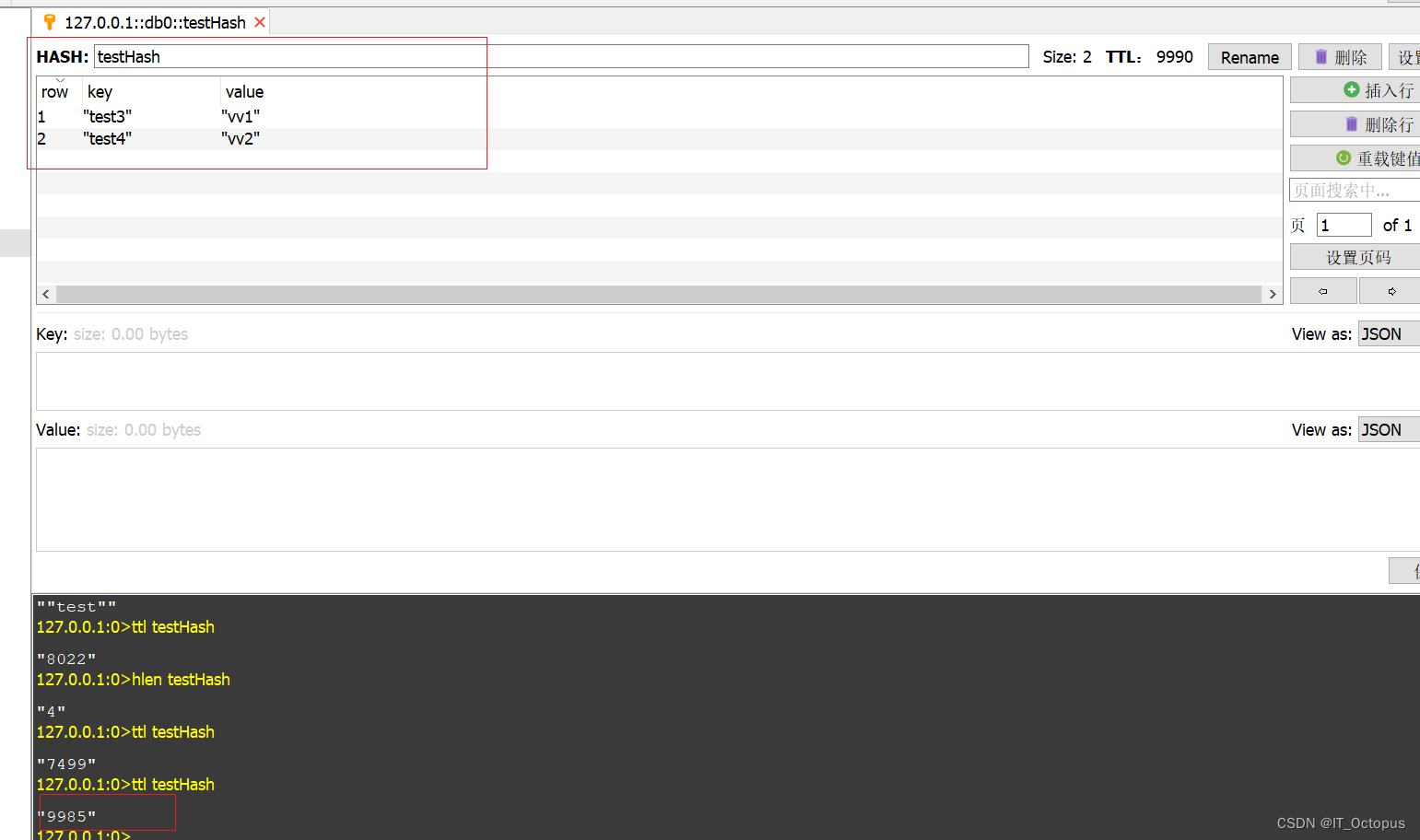
luttuce(RedisTempate)实现hash expire lua脚本
话不多说先放脚本： local argv ARGV local length #argv if length > 0 then local unpackArgs {} for i 1, length - 1 dotable.insert(unpackArgs, argv[i]) end if redis.call(exists, KEYS[1]) 1 thenredis.call(del, KEYS[1])redis.call(hset, KEYS[…...
【Xamarin】WebView连接局域网自动跳转外部浏览器问题的解决
xamarin在中国用的很少，但也有一些独到之处。例如用惯了Visual Studio的就很合适。而且类Java开发，几乎没什么障碍。 protected override void OnCreate(Bundle savedInstanceState) {base.OnCreate(savedInstanceState);Xamarin.Essentials.Platform.I…...
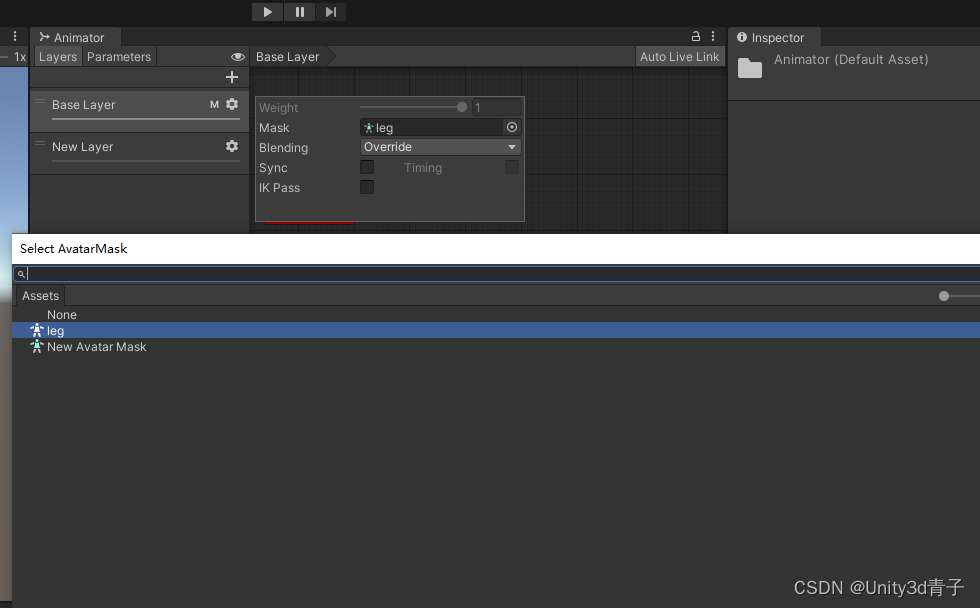
【Unity动画】实现不同的肢体动作自由搭配播放Layer+Avatar Mask
这个教程教你学会使用Unity 动画层配合布偶遮罩（AvaterMask） 实现从2个动画身上只保留部分肢体动作，然后搭配播放 例如：一个正常跑的动画片段，我只保留腿部动作，形成一个层叫Run_leg 然后在从一个攻击动作…...
将0x06（16进制）转换为二进制
将0x06（16进制）转换为二进制，可以按照如下步骤进行： 1. 将0x06中的字母"0x"去除。 2. 将数字"06"中的数字"0"去除。 3. 将数字"06"转换为二进制。 根据步骤1和步骤2，去除&q…...
考PRINCE2有用么？有PMP证书了还需要考PRINCE2吗？
有用的，PMP相当于是理论，PRINCE2是实践，对小白来说pmp考后再考一个prince2是很好的选择，对项目管理的小白来说更好入门。 先来说下 prince 2 和 pmp 的区别 一、prince 2 是什么？跟PMP有什么区别？ prince…...
06进程间关系-学习笔记
Orphan Process孤儿进程 父进程先于子进程退出，子进程失去托管，这种子进程统称为孤儿进程 失效进程（孤儿进程）：导致内存泄漏，影响新进程的创建孤儿进程的危害不可预测，如果一个孤儿进程持续的申…...
Vue的动画方式有几种
Vue的动画方式有几种？ Vue的动画方式主要分成两大类，一类是CSS动画，一类是JS动画 CSS动画中包含transition以及animation，但在Vue中只需要通过transition封装组件实现。 CSS动画的类名主要包括：v-enter、v-enter-acti…...
从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会，其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具，对过去十年 WWDC 主题演讲内容进行了系统化分析，形成了这份…...
令牌桶 滑动窗口-＞限流 分布式信号量-＞限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结： 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析： 实际业务去理解体会统一注…...
Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了，报错如下四、启动不了，解决如下 总结 问题原因 在应用中可以看到chrome，但是打不开(说明：原来的ubuntu系统出问题了，这个是备用的硬盘&a…...
Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统，支持多语言对话（如 中文，英文，日语），语音情感（如 开心，悲伤）&#x…...
（转）什么是DockerCompose?它有什么作用？
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用，而无需手动一个个创建和运行容器。 Compose文件是一个文本文件，通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...
Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...
docker 部署发现spring.profiles.active 问题
报错： org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...
MySQL账号权限管理指南：安全创建账户与精细授权技巧
在MySQL数据库管理中，合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号？ 最小权限原则…...
return this；返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请，不同级别的经理有不同的审批权限： // 抽象处理者：审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...
【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统：Ubuntu 24.04 LTS (WSL2)架构：x86_64 (GNU/Linux)Rust 版本：rustc 1.87.0 (2025-05-09)Cargo 版本：cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...