原点处可微问题
文章目录
- 原点可微问题
- 例
- 例
原点可微问题
- lim x → 0 , y → 0 f ( x , y ) − f ( 0 , 0 ) x 2 + y 2 \lim\limits_{x\to{0},y\to{0}} \frac{f(x,y)-f(0,0)}{\sqrt{x^2+y^2}} x→0,y→0limx2+y2f(x,y)−f(0,0)= 0 0 0
(1)是函数 f ( x , y ) f(x,y) f(x,y)在 ( 0 , 0 ) (0,0) (0,0)点可微(1-1)的充分条件但非必要条件- 考虑到 ρ ( 0 , 0 ) \rho_{(0,0)} ρ(0,0)= x 2 + y 2 \sqrt{x^2+y^2} x2+y2
(2),由式(1)可知, lim x → 0 , y → 0 f ( x , y ) − f ( 0 , 0 ) ρ \lim\limits_{x\to{0},y\to{0}} \frac{f(x,y)-f(0,0)}{\rho} x→0,y→0limρf(x,y)−f(0,0)= 0 0 0(3),由无穷小的阶的定义可知, f ( x , y ) − f ( 0 , 0 ) f(x,y)-f(0,0) f(x,y)−f(0,0)= o ( ρ ) o(\rho) o(ρ)(4),等号左边是 ρ \rho ρ的高阶无穷小 - 由点处可微的定义: f ( x , y ) − f ( x 0 , y 0 ) f(x,y)-f(x_0,y_0) f(x,y)−f(x0,y0)= A d x + B d y + o ( ρ ) A\mathrm{d}x+B\mathrm{d}y+o(\rho) Adx+Bdy+o(ρ)
(5),其中 x 0 = y 0 = 0 x_0=y_0=0 x0=y0=0,从而公式可以改写为: f ( x , y ) − f ( 0 , 0 ) f(x,y)-f(0,0) f(x,y)−f(0,0)= A x + B y + o ( ρ ) Ax+By+o(\rho) Ax+By+o(ρ)(6) - 比较式(4,6)可以发现式(4)是式(6)中 A = B = 0 A=B=0 A=B=0
(6-0)的情形,因此由(1)可以推出函数 f ( x , y ) f(x,y) f(x,y)在(0,0)处可微(6-1),并且 f x ( 0 , 0 ) f_{x}(0,0) fx(0,0)= f y ( 0 , 0 ) f_{y}(0,0) fy(0,0)= 0 0 0(6-2) - 反之,若有(6-1),则有式(6)成立,但是不一定有式(4)成立,也不一定有(1)成立
- 例如取函数 f ( x , y ) f(x,y) f(x,y)= x x x,该函数在 ( 0 , 0 ) (0,0) (0,0)点处可微(满足充分条件),而该函数代入式(1),可得 lim x → 0 , y → 0 x x 2 + y 2 \lim\limits_{x\to{0},y\to{0}} \frac{x}{\sqrt{x^2+y^2}} x→0,y→0limx2+y2x,这个极限不存在,例如沿着 y = 0 y=0 y=0时,就可以发现极限式等于 lim x → 0 , y → 0 x ∣ x ∣ \lim\limits_{x\to{0},y\to{0}} \frac{x}{|x|} x→0,y→0lim∣x∣x不存在(因为可能取 ± 1 \pm{1} ±1,不唯一,就不存在),自然就不满足式(1)
- 若(6-1)的基础上再附加条件 f x ( 0 , 0 ) f_{x}(0,0) fx(0,0)= f y ( 0 , 0 ) f_{y}(0,0) fy(0,0)= 0 0 0,则能推出(1),因为 A = f x ( 0 , 0 ) A=f_{x}(0,0) A=fx(0,0), B = f y ( 0 , 0 ) B=f_{y}(0,0) B=fy(0,0),将(1)代入(6),即得(4),即有(1),这就构成了充要条件
- 即当(6-2)时,(6)和(1)是等价的
- 考虑到 ρ ( 0 , 0 ) \rho_{(0,0)} ρ(0,0)= x 2 + y 2 \sqrt{x^2+y^2} x2+y2
- 拓展:若式(1)改为 lim x → 0 , y → 0 f ( x , y ) − f ( 0 , 0 ) x 2 + y 2 = a ≠ 0 \lim\limits_{x\to{0},y\to{0}} \frac{f(x,y)-f(0,0)}{\sqrt{x^2+y^2}}=a\neq{0} x→0,y→0limx2+y2f(x,y)−f(0,0)=a=0
(8),则没有(4),并且可以得出 f ( x , y ) f(x,y) f(x,y)在 ( 0 , 0 ) (0,0) (0,0)点处不可微(9);另一方面,由(9)推不出(8)
例
- f ( x , y ) f(x,y) f(x,y)= x y sin 1 x 2 + y 2 xy\sin\frac{1}{\sqrt{x^2+y^2}} xysinx2+y21, ( x , y ) ≠ ( 0 , 0 ) (x,y)\neq{(0,0)} (x,y)=(0,0); f ( x , y ) f(x,y) f(x,y)= 0 0 0, ( x , y ) = ( 0 , 0 ) (x,y)=(0,0) (x,y)=(0,0)
- A A A= lim x → 0 , y → 0 f ( x , y ) − f ( 0 , 0 ) x 2 + y 2 \lim\limits_{x\to{0},y\to{0}} \frac{f(x,y)-f(0,0)}{\sqrt{x^2+y^2}} x→0,y→0limx2+y2f(x,y)−f(0,0)= lim x → 0 , y → 0 f ( x , y ) x 2 + y 2 \lim\limits_{x\to{0},y\to{0}} \frac{f(x,y)}{\sqrt{x^2+y^2}} x→0,y→0limx2+y2f(x,y)= 0 0 0,立马可以判断处 f ( x , y ) f(x,y) f(x,y)在 ( 0 , 0 ) (0,0) (0,0)处可微
- 其中 A A A= lim x → 0 , y → 0 x y x 2 + y 2 sin 1 x 2 + y 2 \lim\limits_{x\to{0},y\to{0}} \frac{xy}{{\sqrt{x^2+y^2}}} \sin\frac{1}{\sqrt{x^2+y^2}} x→0,y→0limx2+y2xysinx2+y21,其中 A 1 A_1 A1= lim x → 0 , y → 0 x y x 2 + y 2 \lim\limits_{x\to{0},y\to{0}} \frac{xy}{\sqrt{x^2+y^2}} x→0,y→0limx2+y2xy= 0 0 0,
- 可以用夹逼的方式求: 0 ⩽ ∣ x y x 2 + y 2 ∣ 0\leqslant|\frac{xy}{\sqrt{x^2+y^2}}| 0⩽∣x2+y2xy∣= ∣ x x 2 + y 2 ∣ ∣ y ∣ |\frac{x}{\sqrt{x^2+y^2}}||y| ∣x2+y2x∣∣y∣ ⩽ \leqslant ⩽ ∣ y ∣ |y| ∣y∣,而 lim x → 0 , y → 0 ∣ y ∣ = 0 \lim\limits_{x\to{0},y\to{0}} |y|=0 x→0,y→0lim∣y∣=0所以 lim x → 0 , y → 0 ∣ x y x 2 + y 2 ∣ = 0 \lim\limits_{x\to{0},y\to{0}} |\frac{xy}{\sqrt{x^2+y^2}}|=0 x→0,y→0lim∣x2+y2xy∣=0,所以 A 1 A_1 A1=0
- 从量级上粗略判断: x y xy xy和 x 2 + y 2 \sqrt{x^2+y^2} x2+y2分别相当于 2 2 2次和1次项,因此分子的阶更高,极限结果为0
- 而 sin 1 x 2 + y 2 \sin\frac{1}{\sqrt{x^2+y^2}} sinx2+y21是有界函数,从而 A A A=0
例
- f ( x , y ) f(x,y) f(x,y)= x 2 y x 2 + y 2 \frac{x^2y}{x^2+y^2} x2+y2x2y, ( x , y ) ≠ ( 0 , 0 ) (x,y)\neq{(0,0)} (x,y)=(0,0); f ( x , y ) = 0 f(x,y)=0 f(x,y)=0, ( x , y ) = ( 0 , 0 ) (x,y)=(0,0) (x,y)=(0,0)
- A A A= lim x → 0 , y → 0 f ( x , y ) − f ( 0 , 0 ) x 2 + y 2 \lim\limits_{x\to{0},y\to{0}} \frac{f(x,y)-f(0,0)}{\sqrt{x^2+y^2}} x→0,y→0limx2+y2f(x,y)−f(0,0)= lim x → 0 , y → 0 x 2 y ( x 2 + y 2 ) x 2 + y 2 \lim\limits_{x\to{0},y\to{0}} \frac{x^2y}{(x^2+y^2)\sqrt{x^2+y^2}} x→0,y→0lim(x2+y2)x2+y2x2y,简便判断分子分母都是3次项的量级(同量级),因此极限不存在(可取路径 y = x y=x y=x判断)
- 而 f x ( 0 , 0 ) f_x(0,0) fx(0,0)= f y ( 0 , 0 ) f_{y}(0,0) fy(0,0)= 0 0 0,而 A A A不存在,所以 f ( x , y ) f(x,y) f(x,y)在(0,0)处不可微
- 求 f x ( 0 , 0 ) f_x(0,0) fx(0,0),可以先代入 y = 0 y=0 y=0后求对 x x x偏导,即对 f ( x , 0 ) f(x,0) f(x,0)对 x x x求导
- 而 f ( x , 0 ) f(x,0) f(x,0)= { 0 x ≠ 0 0 x = 0 \begin{cases}0&x\neq{0}\\0&x=0\end{cases} {00x=0x=0= 0 0 0,说明 f ( x , 0 ) f(x,0) f(x,0)是个恒0常数函数,类似的, f ( 0 , y ) f(0,y) f(0,y)也是恒0常数函数
- 所以 f x ( 0 , 0 ) f_{x}(0,0) fx(0,0)= f ( x , 0 ) ′ f(x,0)' f(x,0)′= 0 0 0
- f y ( 0 , 0 ) f_{y}(0,0) fy(0,0)= f ′ ( 0 , y ) f'(0,y) f′(0,y)= 0 0 0
相关文章:

原点处可微问题
文章目录 原点可微问题例例 原点可微问题 lim x → 0 , y → 0 f ( x , y ) − f ( 0 , 0 ) x 2 y 2 \lim\limits_{x\to{0},y\to{0}} \frac{f(x,y)-f(0,0)}{\sqrt{x^2y^2}} x→0,y→0limx2y2 f(x,y)−f(0,0) 0 0 0(1)是函数 f ( x , y ) f(x,y) f(x,y)在 ( 0 , 0 ) (…...
Flink+Kafka消费
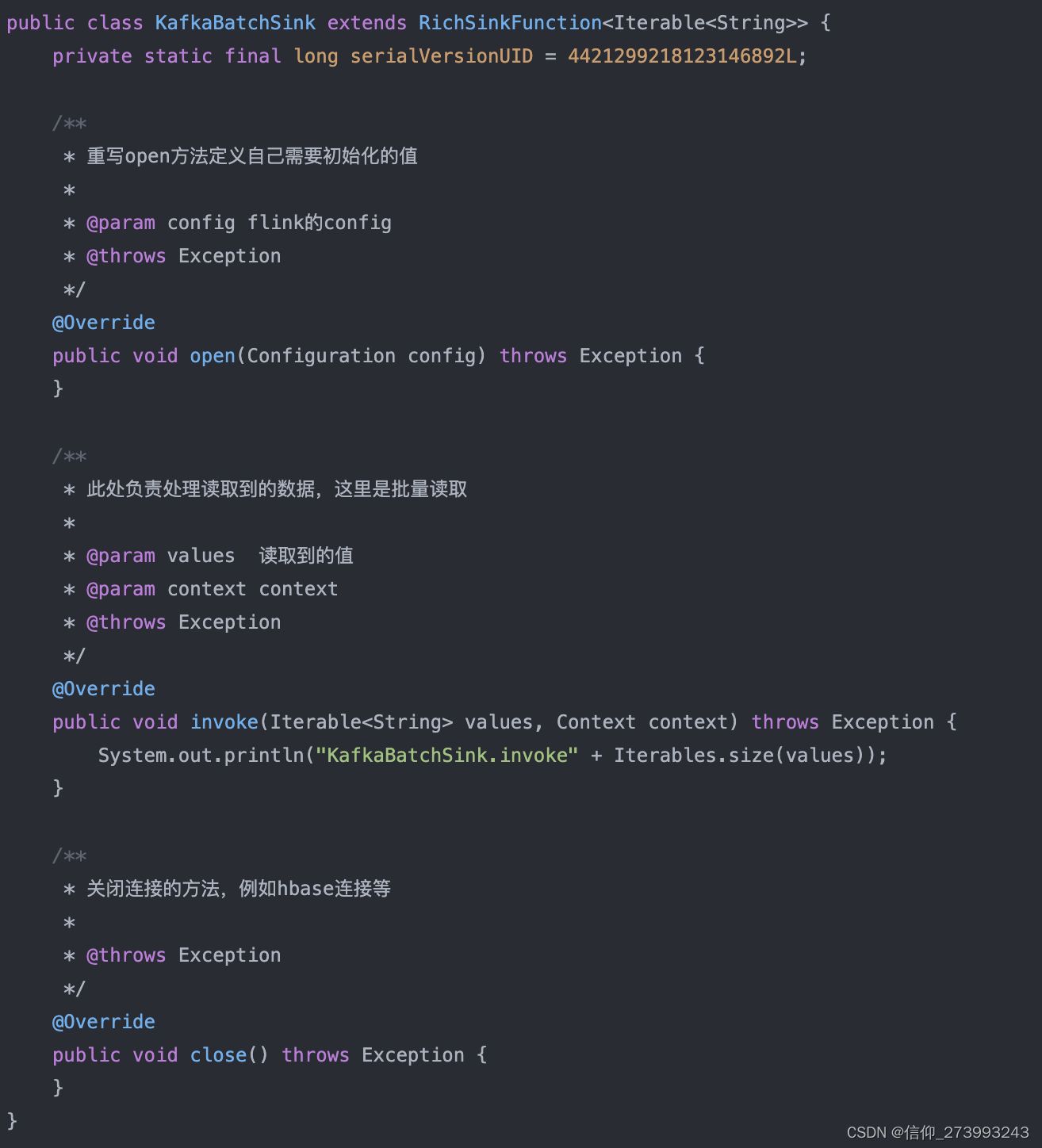
引入jar <dependency><groupId>org.apache.flink</groupId><artifactId>flink-java</artifactId><version>1.8.0</version> </dependency> <dependency><groupId>org.apache.flink</groupId><artifactI…...

Seconds_Behind_Master越来越大,主从同步延迟
问题现象 发现从库mysql_slave的参数Seconds_Behind_Master越来越大。已排除主从服务器时间不一致;那么主要就判断两点:是io thread慢还是 sql thread慢?先观察show slave status\G 。 判断3个参数(参数后面的值是默认空闲时候的…...

除法求值[中等]
一、题目 给你一个变量对数组equations和一个实数值数组values作为已知条件,其中equations[i] [Ai, Bi]和values[i]共同表示等式Ai / Bi values[i]。每个Ai或Bi是一个表示单个变量的字符串。另有一些以数组queries表示的问题,其中queries[j] [Cj, Dj…...

新时代商业市场:AR技术的挑战与机遇并存
随着科技的不断发展,增强现实(AR)技术逐渐成为当今社会的一个重要组成部分。AR技术能够将虚拟世界与现实世界相结合,为人们提供更加丰富、多样化的体验。在新时代的社会商业市场中,AR技术也正逐渐被应用于各种商业活动…...

RHEL8中ansible的使用
编写ansible.cfg和清单文件ansible的基本用法 本章实验三台RHEL8系统(rhel801,rhel802,rhel803),其中rhel801是ansible主机 这里要确保ansible主机能够解析所有被管理的机器,这里通过配置/etc/hosts来实现…...

【1.6计算机组成与体系结构】存储系统
目录 1.层次化存储结构2.Cache2.1 Cache的介绍2.2 局部性原理2.3 Cache应用 1.层次化存储结构 由 ⬆ CPU:寄存器。 快 ⬆ Cache:按内容存取(相联存储器)。 到 ⬆内存(主存):DRAM。 慢 ⬆ 外存(辅存&#…...
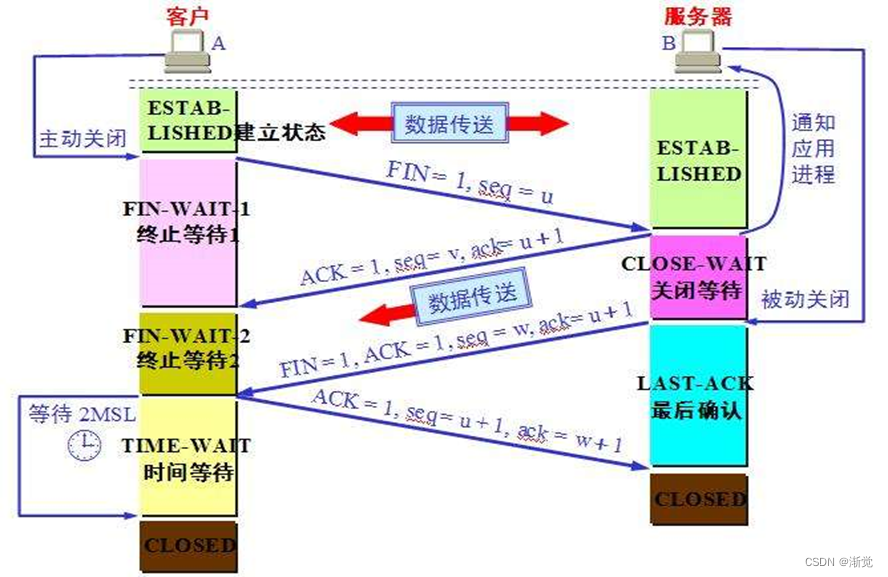
TCP/UDP 协议
目录 一.TCP协议 1.介绍 2.报文格式 编辑 确认号 控制位 窗口大小 3.TCP特性 二.TCP协议的三次握手 1.tcp 三次握手的过程 三.四次挥手 2.有限状态机 四.tcp协议和udp协议的区别 五.udp协议 UDP特性 六.telnet协议 一.TCP协议 1.介绍 TCP(Transm…...

如何正确理解和使用 Golang 中 nil ?
目录 指针中的 nil 切片中的 nil map 中的 nil 通道中的 nil 函数中的 nil 接口中的 nil 避免 nil 相关问题的最佳实践 小结 在 Golang 中,nil 是一个预定义的标识符,在不同的上下文环境中有不同的含义,但通常表示“无”、“空”或“…...
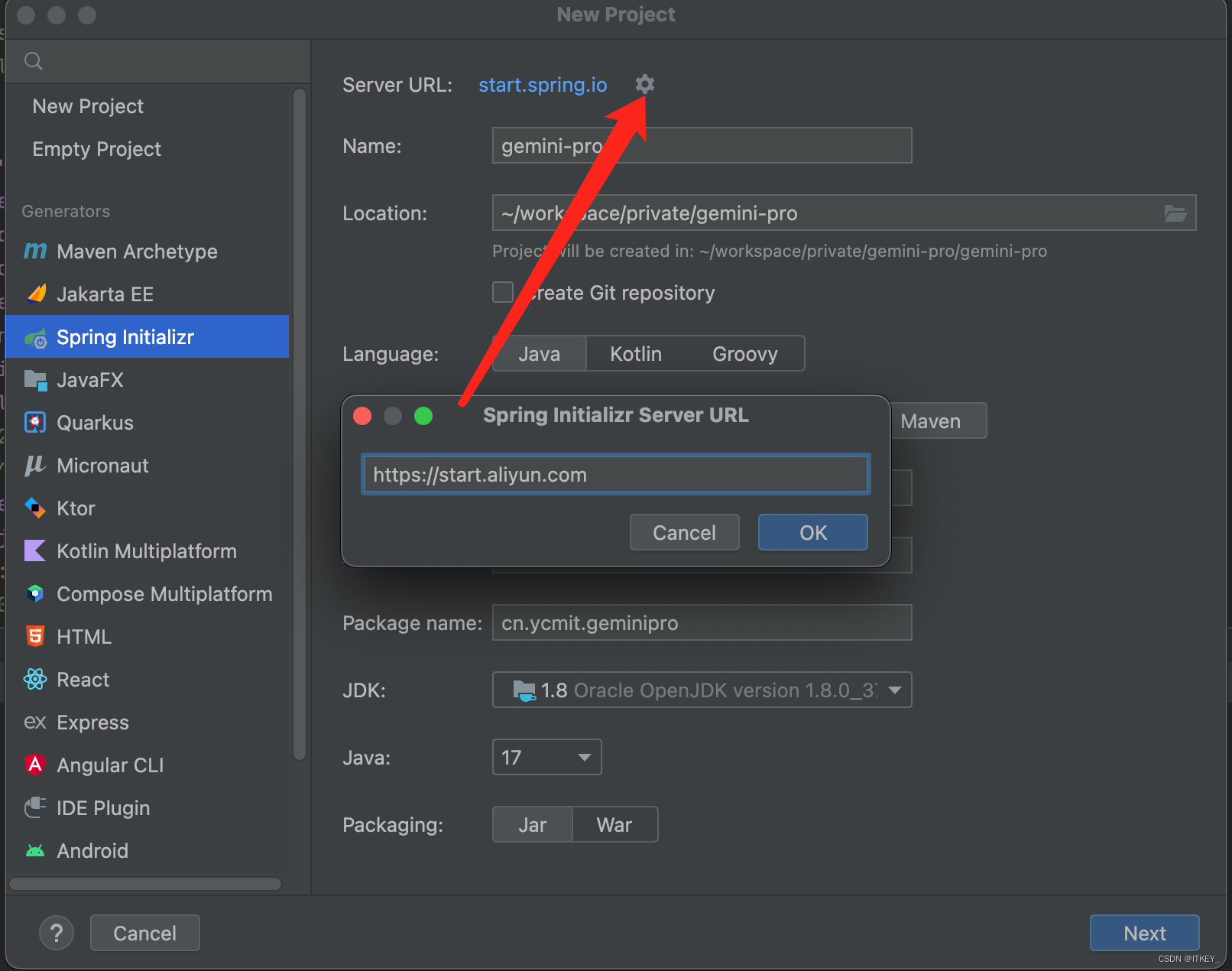
IDEA新建jdk8 spring boot项目
今天新建spring boot项目发现JDK版本最低可选17。 但是目前用的最多的还是JDK8啊。 解决办法 Server URL中设置: https://start.aliyun.com/设置完成后,又可以愉快的用jdk8创建项目了。 参考 https://blog.csdn.net/imbzz/article/details/13469117…...

Qt/C++音视频开发59-使用mdk-sdk组件/原qtav作者力作/性能凶残/超级跨平台
一、前言 最近一个月一直在研究mdk-sdk音视频组件,这个组件是原qtav作者的最新力作,提供了各种各样的示例demo,不仅限于支持C,其他各种比如java/flutter/web/android等全部支持,性能上也是杠杠的,目前大概…...

智安网络|企业网络安全工具对比:云桌面与堡垒机,哪个更适合您的需求
随着云计算技术的快速发展,越来越多的企业开始采用云计算解决方案来提高效率和灵活性。在云计算环境下,云桌面和堡垒机被广泛应用于企业网络安全和办公环境中。尽管它们都有助于提升企业的安全和效率,但云桌面和堡垒机在功能和应用方面存在着…...
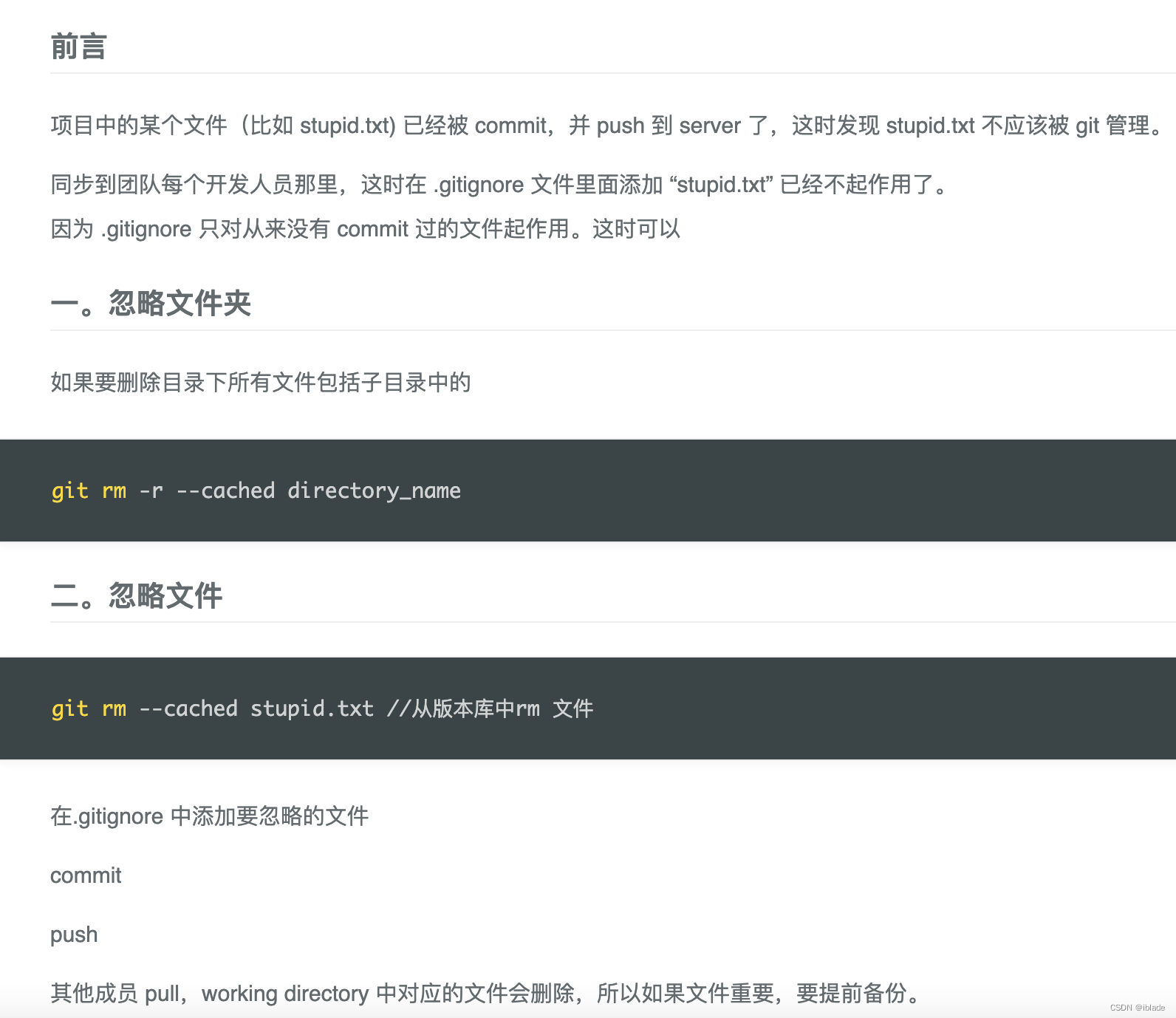
Git忽略已经提交的文件
原理类似于 Android修改submodule的lib包名...

MVVM和MVC以及MVP的原理以及它们的区别
MVVM、MVC 和 MVP 都是前端架构模式,它们各自有不同的原理和特点。 MVC(Model-View-Controller) 原理:MVC 将应用程序分为三个部分:模型(Model)、视图(View)和控制器&a…...
WeChatMsg: 导出微信聊天记录 | 开源日报 No.108
Mozilla-Ocho/llamafile Stars: 3.5k License: NOASSERTION llamafile 是一个开源项目,旨在通过将 lama.cpp 与 Cosmopolitan Libc 结合成一个框架,将 LLM (Large Language Models) 的复杂性折叠到单个文件可执行程序中,并使其能够在大多数…...
)
Python学习之复习MySQL-Day3(DQL)
目录 文章声明⭐⭐⭐让我们开始今天的学习吧!DQL简介基本查询查询多个/全部字段设置别名去除重复记录 条件查询条件查询介绍实例演示 聚合函数什么是聚合函数?常见的聚合函数实例演示 分组查询分组查询语法where 和 having 的区别实例演示 排序查询语法实…...

AI超级个体:ChatGPT与AIGC实战指南
目录 前言 一、ChatGPT在日常工作中的应用场景 1. 客户服务与支持 2. 内部沟通与协作 3. 创新与问题解决 二、巧用ChatGPT提升工作效率 1. 自动化工作流程 2. 信息整合与共享 3. 提高决策效率 三、巧用ChatGPT创造价值 1. 优化产品和服务 2. 提高员工满意度和留任率…...
|(使用OkHttpClient实现websocket以及详细介绍))
SpringBoot集成websocket(5)|(使用OkHttpClient实现websocket以及详细介绍)
SpringBoot集成websocket(5)|(使用OkHttpClient实现websocket以及详细介绍) 文章目录 SpringBoot集成websocket(5)|(使用OkHttpClient实现websocket以及详细介绍)[TOC] 前言一、初始…...
Kafka-Kafka基本原理与集群快速搭建(实践)
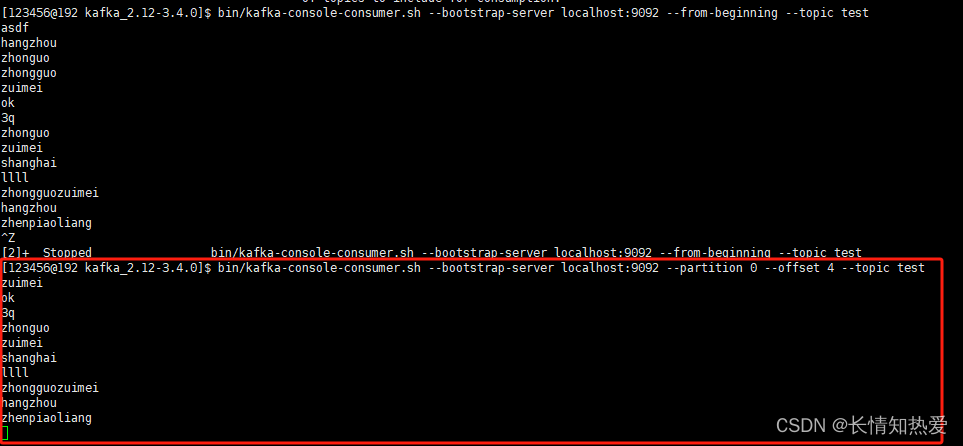
Kafka单机搭建 下载Kafka Apache Download Mirrors 解压 tar -zxvf kafka_2.12-3.4.0.tgz -C /usr/local/src/software/kafkakafka内部bin目录下有个内置的zookeeper(用于单机) 启动zookeeper(在后台启动) nohup bin/zookeeper-server-start.sh conf…...
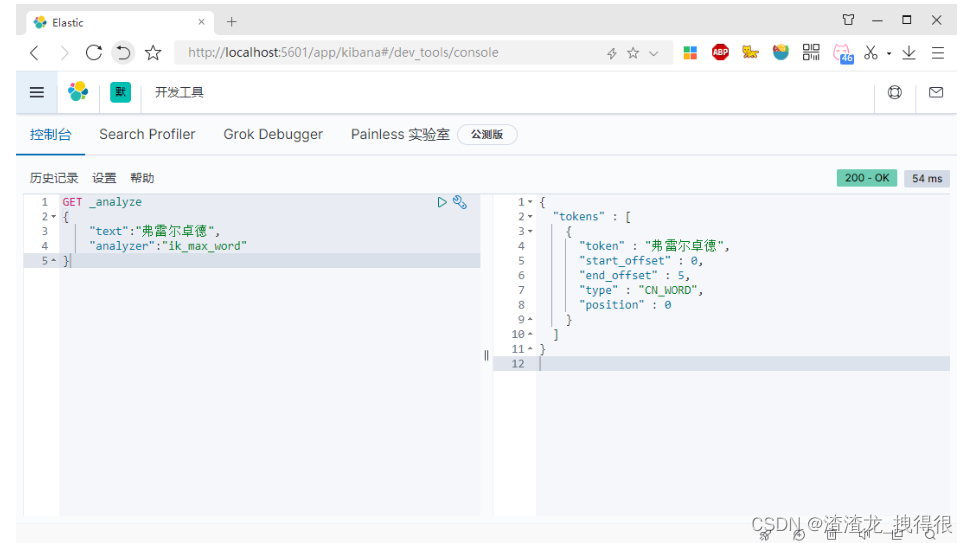
Elasticsearch 进阶(索引、类型、字段、分片、副本、集群等详细说明)-06
笔记来源:Elasticsearch Elasticsearch进阶 进阶-核心概念 索引Index 一个索引就是一个拥有几分相似特征的文档的集合。比如说,你可以有一个客户数据的索引,另一个产品目录的索引,还有一个订单数据的索引。一个索引由一个名字…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...

图解JavaScript原型:原型链及其分析 | JavaScript图解
忽略该图的细节(如内存地址值没有用二进制) 以下是对该图进一步的理解和总结 1. JS 对象概念的辨析 对象是什么:保存在堆中一块区域,同时在栈中有一块区域保存其在堆中的地址(也就是我们通常说的该变量指向谁&…...
