位运算(、|、^、~、>>、<<)
分类 编程技术
1.位运算概述
从现代计算机中所有的数据二进制的形式存储在设备中。即 0、1 两种状态,计算机对二进制数据进行的运算(+、-、*、/)都是叫位运算,即将符号位共同参与运算的运算。
口说无凭,举一个简单的例子来看下 CPU 是如何进行计算的,比如这行代码:
int a = 35; int b = 47; int c = a + b;
计算两个数的和,因为在计算机中都是以二进制来进行运算,所以上面我们所给的 int 变量会在机器内部先转换为二进制在进行相加:
35: 0 0 1 0 0 0 1 1 47: 0 0 1 0 1 1 1 1 ———————————————————— 82: 0 1 0 1 0 0 1 0
所以,相比在代码中直接使用(+、-、*、/)运算符,合理的运用位运算更能显著提高代码在机器上的执行效率。
2.位运算概览
| 符号 | 描述 | 运算规则 |
|---|---|---|
| & | 与 | 两个位都为1时,结果才为1 |
| | | 或 | 两个位都为0时,结果才为0 |
| ^ | 异或 | 两个位相同为0,相异为1 |
| ~ | 取反 | 0变1,1变0 |
| << | 左移 | 各二进位全部左移若干位,高位丢弃,低位补0 |
| >> | 右移 | 各二进位全部右移若干位,对无符号数,高位补0,有符号数,各编译器处理方法不一样,有的补符号位(算术右移),有的补0(逻辑右移) |
3.按位与运算符(&)#
定义:参加运算的两个数据,按二进制位进行"与"运算。
运算规则:
0&0=0 0&1=0 1&0=0 1&1=1
总结:两位同时为1,结果才为1,否则结果为0。
例如:3&5 即 0000 0011& 0000 0101 = 0000 0001,因此 3&5 的值得1。
注意:负数按补码形式参加按位与运算。
与运算的用途:
1)清零
如果想将一个单元清零,即使其全部二进制位为0,只要与一个各位都为零的数值相与,结果为零。
2)取一个数的指定位
比如取数 X=1010 1110 的低4位,只需要另找一个数Y,令Y的低4位为1,其余位为0,即Y=0000 1111,然后将X与Y进行按位与运算(X&Y=0000 1110)即可得到X的指定位。
3)判断奇偶
只要根据最未位是0还是1来决定,为0就是偶数,为1就是奇数。因此可以用if ((a & 1) == 0)代替if (a % 2 == 0)来判断a是不是偶数。
4.按位或运算符(|)
定义:参加运算的两个对象,按二进制位进行"或"运算。
运算规则:
0|0=0 0|1=1 1|0=1 1|1=1
总结:参加运算的两个对象只要有一个为1,其值为1。
例如:3|5即 0000 0011| 0000 0101 = 0000 0111,因此,3|5的值得7。
注意:负数按补码形式参加按位或运算。
或运算的用途:
1)常用来对一个数据的某些位设置为1
比如将数 X=1010 1110 的低4位设置为1,只需要另找一个数Y,令Y的低4位为1,其余位为0,即Y=0000 1111,然后将X与Y进行按位或运算(X|Y=1010 1111)即可得到。
5.异或运算符(^)
定义:参加运算的两个数据,按二进制位进行"异或"运算。
运算规则:
0^0=0 0^1=1 1^0=1 1^1=0
总结:参加运算的两个对象,如果两个相应位相同为0,相异为1。
异或的几条性质:
- 1、交换律
- 2、结合律 (a^b)^c == a^(b^c)
- 3、对于任何数x,都有 x^x=0,x^0=x
- 4、自反性: a^b^b=a^0=a;
异或运算的用途:
1)翻转指定位
比如将数 X=1010 1110 的低4位进行翻转,只需要另找一个数Y,令Y的低4位为1,其余位为0,即Y=0000 1111,然后将X与Y进行异或运算(X^Y=1010 0001)即可得到。
2)与0相异或值不变
例如:1010 1110 ^ 0000 0000 = 1010 1110
3)交换两个数
实例
void Swap(int &a, int &b){
if (a != b){
a ^= b;
b ^= a;
a ^= b;
}
}
6.取反运算符 (~)
定义:参加运算的一个数据,按二进制进行"取反"运算。
运算规则:
~1=0 ~0=1
总结:对一个二进制数按位取反,即将0变1,1变0。
异或运算的用途:
1)使一个数的最低位为零
使a的最低位为0,可以表示为:a & ~1。~1的值为 1111 1111 1111 1110,再按"与"运算,最低位一定为0。因为" ~"运算符的优先级比算术运算符、关系运算符、逻辑运算符和其他运算符都高。
7.左移运算符(<<)
定义:将一个运算对象的各二进制位全部左移若干位(左边的二进制位丢弃,右边补0)。
设 a=1010 1110,a = a<< 2 将a的二进制位左移2位、右补0,即得a=1011 1000。
若左移时舍弃的高位不包含1,则每左移一位,相当于该数乘以2。
8.右移运算符(>>)
定义:将一个数的各二进制位全部右移若干位,正数左补0,负数左补1,右边丢弃。
例如:a=a>>2 将a的二进制位右移2位,左补0 或者 左补1得看被移数是正还是负。
操作数每右移一位,相当于该数除以2。
10.复合赋值运算符
位运算符与赋值运算符结合,组成新的复合赋值运算符,它们是:
&= 例:a&=b 相当于 a=a&b|= 例:a|=b 相当于 a=a|b>>= 例:a>>=b 相当于 a=a>>b<<= 例:a<<=b 相当于 a=a<<b^= 例:a^=b 相当于 a=a^b
运算规则:和前面讲的复合赋值运算符的运算规则相似。
不同长度的数据进行位运算:如果两个不同长度的数据进行位运算时,系统会将二者按右端对齐,然后进行位运算。
以"与运算"为例说明如下:我们知道在C语言中long型占4个字节,int型占2个字节,如果一个long型数据与一个int型数据进行"与运算",右端对齐后,左边不足的位依下面三种情况补足,
- 1)如果整型数据为正数,左边补16个0。
- 2)如果整型数据为负数,左边补16个1。
- 3)如果整形数据为无符号数,左边也补16个0。
- 如:long a=123;int b=1;计算a& b。
如:long a=123;int b=-1;计算a& b。
如:long a=123;unsigned intb=1;计算a & b。
相关文章:
)
位运算(、|、^、~、>>、<<)
分类 编程技术 1.位运算概述 从现代计算机中所有的数据二进制的形式存储在设备中。即 0、1 两种状态,计算机对二进制数据进行的运算(、-、*、/)都是叫位运算,即将符号位共同参与运算的运算。 口说无凭,举一个简单的例子来看下 CPU 是如何进…...
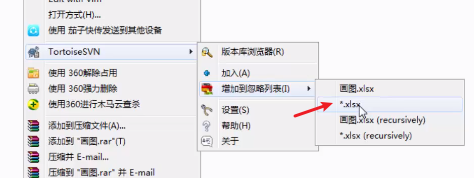
Centos7部署SVN
文章目录 (1)SVN概述(2)SVN与Samba共享(3)安装SVN(4)SVN搭建实例(5)pc连接svn服务器(6)svn图标所代表含义 (1)…...

Vue中this.$nextTick的执行时机
一、Vue中this.$nextTick的执行时机,整体可分为两种情况: 第一种:下一次 Dom 更新之后执行(即等待DOM更新结束之后,执行nextTick的延迟回调函数); 第二种:页面挂载后 (m…...

Unity中的ShaderToy
文章目录 前言一、ShaderToy网站二、ShaderToy基本框架1、我们可以在ShaderToy网站中,这样看用到的GLSL文档2、void mainImage 是我们的程序入口,类似于片断着色器3、fragColor作为输出变量,为屏幕每一像素的颜色,alpha一般赋值为…...
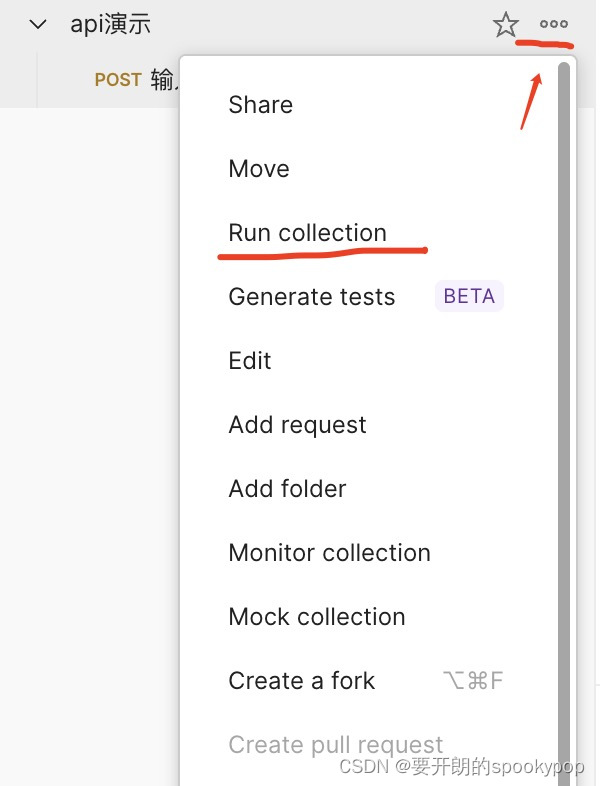
2 使用postman进行接口测试
上一篇:1 接口测试介绍-CSDN博客 拿到开发提供的接口文档后,结合需求文档开始做接口测试用例设计,下面用最常见也最简单的注册功能介绍整个流程。 说明:以演示接口测试流程为主,不对演示功能做详细的测试,…...

【数据库设计和SQL基础语法】--查询数据--聚合函数
一、聚合函数概述 1.1 定义 聚合函数是一类在数据库中用于对多个行进行计算并返回单个结果的函数。它们能够对数据进行汇总、统计和计算,常用于提取有关数据集的摘要信息。聚合函数在 SQL 查询中广泛应用,包括统计总数、平均值、最大值、最小值等。 1…...
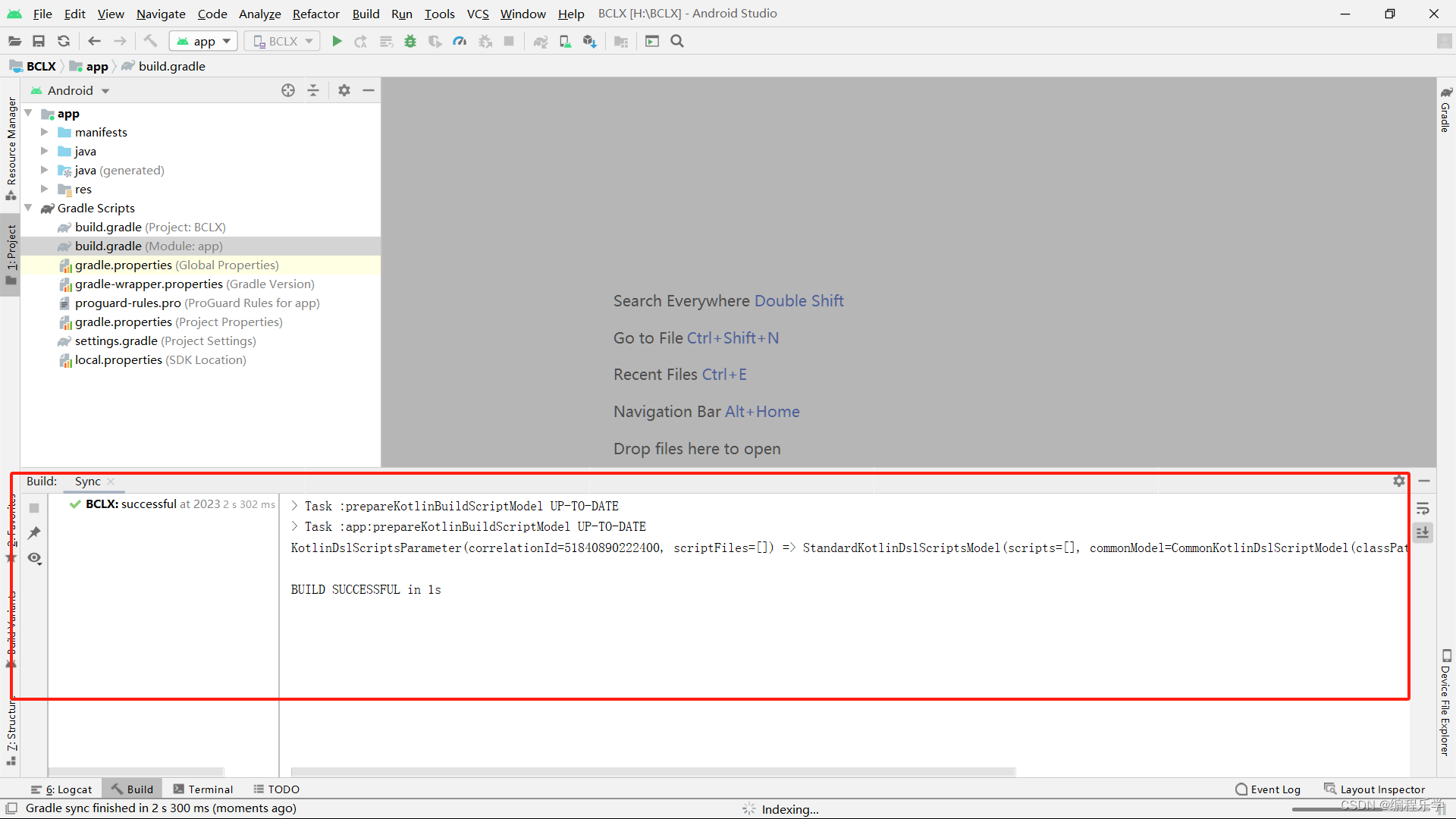
Module ‘app‘: platform ‘android-33‘ not found.
目录 一、报错信息 二、解决方法 一、报错信息 Module app: platform android-33 not found. 检查你的应用程序的build.gradle文件中的targetSdkVersion和compileSdkVersion是否正确设置为已安装的Android SDK版本。 确保你的Android Studio已正确安装并配置了所需的Android …...

MySQL按序批量操作大量数据
MySQL按序批量操作大量数据(Java、springboot、mybatisplus、ElasticSearch) 以同步全量MySQL数据到ElasticSearch为例。 核心代码 业务逻辑: public boolean syncToElasticsearch() {log.info("Starting data synchronization to El…...
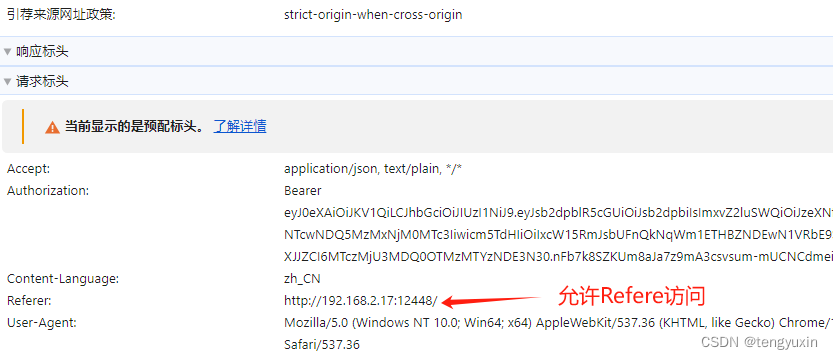
strict-origin-when-cross-origin
严格限制同源策略 (1)允许服务器的同源IP地址访问 (2)允许Referer --- 后端服务器要配置...

【置顶】 本博博文汇总
文章目录 前言音视频ijkplayer源码分析FFmpeg、音视频协议Andriod系统音视频框架C、C Android&Java源码分析、绘制、渲染Dalvik、Art虚拟机Java并发 计算机基础操作系统计算机网络设计模式、数据结构、算法 前言 23年底了,想来也工作十年,也一直在c…...
react.js源码二
三、调度Scheduler scheduling(调度)是fiber reconciliation的一个过程,主要决定应该在何时做什么?在stack reconciler中,reconciliation是“一气呵成”,对于函数来说,这没什么问题,因为我们只想要函数的运行结果,但对于UI来说还需要考虑以下问题: 并不是所有的state更…...

如何学习英语
前言 首先写一些自己的感言吧,其实从大学的时候就在不断地听英语,学英语,但是到毕业十几年后,英语一直没起到什么作用,当然最有作用的时候就是几次英语面试吧。 工作之后有一段学习英语的经历,当时花费了…...

robot测试自动化
一. 安装 黑羽robot 首先确保你电脑上安装好了 Python 3.7 或者 3.8 版本的解释器 hyrobot 使用说明1 | 白月黑羽 安装RF 黑羽robot基于Robot Framework ,所以必须先安装RobotFramework 直接执行如下Pip命令即可: pip install robotframework...
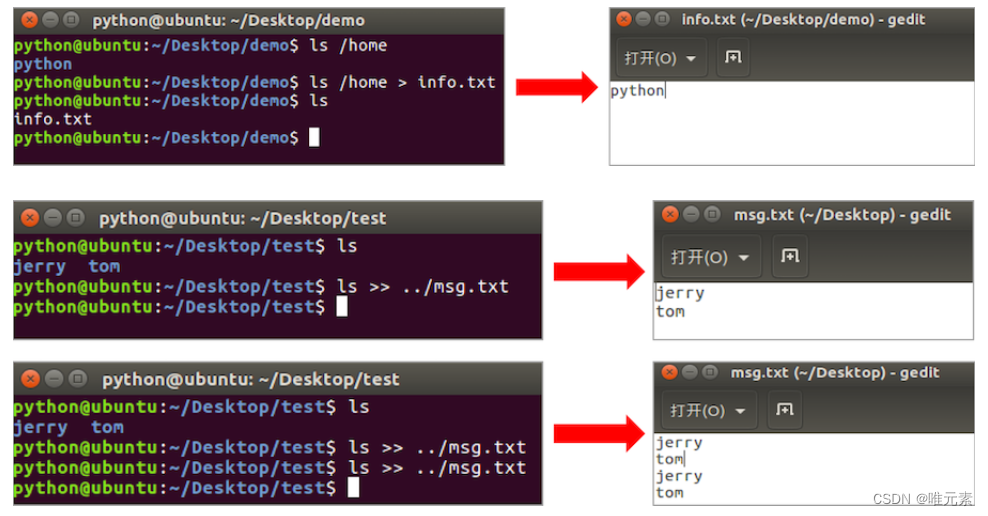
Linux---重定向命令
1. 重定向命令的介绍 重定向也称为输出重定向,把在终端执行命令的结果保存到目标文件。 2. 重定向命令的使用 命令说明>如果文件存在会覆盖原有文件内容,相当于文件操作中的‘w’模式>>如果文件存在会追加写入文件末尾,相当于文件…...

小区生活污水处理需要哪些设备和工艺
在小区生活中,污水处理是一个非常重要的环节,它关乎到环境的保护和居民的生活质量。因此,了解小区生活污水处理所需要的设备和工艺是至关重要的。 首先,在小区生活污水处理中,需要用到的设备包括污水收集系统、初级沉淀…...

【高性能计算】Cpp + Eigen + Intel MKL + 函数写成传引用
CUDA加速原理:CUDA编程学习:自定义Pytorch+cpp/cuda extension 高质量C++进阶[2]:如何让线性代数加速1000倍? 【gcc, cmake, eigen, opencv,ubuntu】三.eigen和mkl安装和使用 Linux下MKL库的安装部署与使用,并利用cmake编译器调用MKL库去提升eigen库的计算速度 Eigen库…...

【教学类-05-02】20231216 (比大小> <=)X-Y之间的比大小88题(补全88格子,有空格分割提示)
作品展示: 背景需求: 1、以前做过一份比大小的题目 【教学类-05-01】20211018 Python VSC 大班 数字比大小(> <)_vsc比较3位数大小-CSDN博客文章浏览阅读674次。【教学类-05-01】20211018 Python VSC 大班…...
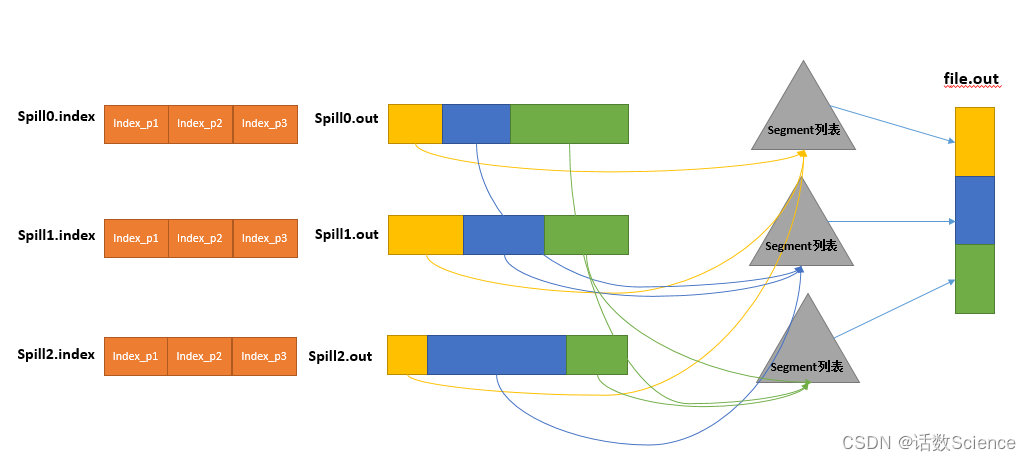
【Spark精讲】Spark与MapReduce对比
目录 对比总结 MapReduce流程 编辑 MapTask流程 ReduceTask流程 MapReduce原理 阶段划分 Map shuffle Partition Collector Sort Spill Merge Reduce shuffle Copy Merge Sort 对比总结 Map端读取文件:都是需要通过split概念来进行逻辑切片&…...
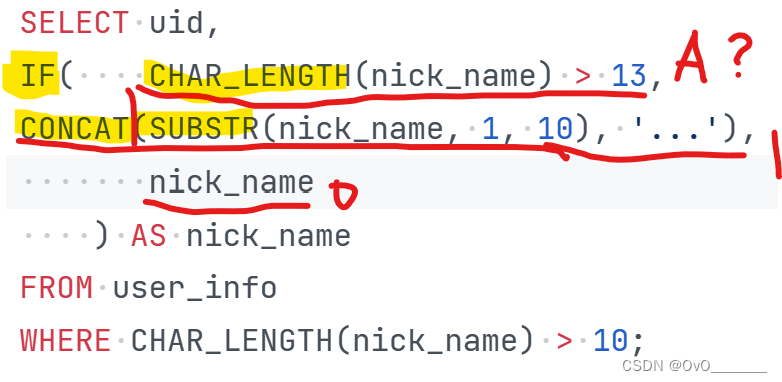
SQL错题集3
1.薪水第二多的员工的emp_no以及其对应的薪水salary limit a,b 其中a表示查询数据的起始位置,b表示返回的数量。 (MySQL数据库中的记录是从0开始的) 注意从0开始 2.员工编号emp_no为10001其自入职以来的薪水salary涨幅值growth 聚合函数不能…...
Elasticsearch:使用 OpenAI 生成嵌入并进行向量搜索 - nodejs
在我之前的文章: Elasticsearch:使用 Open AI 和 Langchain 的 RAG - Retrieval Augmented Generation (一)(二)(三)(四) 我详细地描述了如何使用…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...
