应用统计部分常用公式总结
常见分布函数
常用公式
- 分位数:P{X>xα}=α,P{X≤xα}=1−αP\{X>x_\alpha\}=\alpha, P\{X\le x_\alpha\}=1-\alphaP{X>xα}=α,P{X≤xα}=1−α
- E(Xi)=E(X)=E(X‾)=μE(X_i)=E(X)=E(\overline X)=\muE(Xi)=E(X)=E(X)=μ
- E(X2)=E2(X)+D(X)=μ2+σ2E(X^2)=E^2(X)+D(X)=\mu^2+\sigma^2E(X2)=E2(X)+D(X)=μ2+σ2
- D(X‾)=1nD(X)=σ2nD(\overline X)=\frac{1}{n}D(X)=\frac{\sigma^2}{n}D(X)=n1D(X)=nσ2
- 若X∼N(0,σ2)X\sim N(0,\sigma^2)X∼N(0,σ2)则:E(Xn)={0,n=1,3,5…σn(n−1)(n−3)…1,n=2,4,6…E(X^n)=\begin{cases}0,&n=1,3,5\dots\\\sigma^n(n-1)(n-3)\dots1,&n=2,4,6\dots\end{cases}E(Xn)={0,σn(n−1)(n−3)…1,n=1,3,5…n=2,4,6…
- nnn足够大时(n>45n>45n>45),Xα≈n+2nZα,tα(n)≈ZαX_\alpha\approx n+\sqrt{2n}Z_\alpha,\quad t_\alpha(n)\approx Z_\alphaXα≈n+2nZα,tα(n)≈Zα
离散分布
-
二项分布
X∼B(n,p)X\sim B(n,p)X∼B(n,p)则:
- P(X=x)=Cnxpx(1−p)n−xP(X=x)=C_n^xp^x(1-p)^{n-x}P(X=x)=Cnxpx(1−p)n−x
- E(X)=npE(X)=npE(X)=np
- D(X)=np(1−p)D(X)=np(1-p)D(X)=np(1−p)
-
泊松分布
X∼P(λ)X\sim P(\lambda)X∼P(λ)则:
- P(X=x)=λxe−λx!,x=0,1,2,…P(X=x)=\frac{\lambda^xe^{-\lambda}}{x!},\quad x=0,1,2,\dotsP(X=x)=x!λxe−λ,x=0,1,2,…
- E(X)=D(X)=λE(X)=D(X)=\lambdaE(X)=D(X)=λ
连续分布
| 分布 | 简介 | E(X)E(X)E(X) | D(X)D(X)D(X) |
|---|---|---|---|
| 伽马分布 p9 | 指数分布和卡方分布的推广形式 | αλ\frac{\alpha}{\lambda}λα | αλ2\frac{\alpha}{\lambda^2}λ2α |
| 卡方分布 | 标准正态分布的平方和 | nnn | 2n2n2n |
| t分布 | 标准正态χ2(n)/n\frac{标准正态}{\sqrt{\chi^2(n)/n}}χ2(n)/n标准正态 | \ | \ |
| F分布 | 卡方分布的比 | \ | \ |
-
均匀分布
X∼U(a,b)X\sim U(a,b)X∼U(a,b)则:
- E(X)=a+b2E(X)=\frac{a+b}{2}E(X)=2a+b
- D(X)=(b−a)212D(X)=\frac{(b-a)^2}{12}D(X)=12(b−a)2
-
泊松分布
X∼P(λ)X\sim P(\lambda)X∼P(λ)
- P(X=x)=λxx!e−λx=1,2,3,…P(X=x)=\frac{\lambda^{x}}{x!}e^{-\lambda}\quad x=1,2,3,\dotsP(X=x)=x!λxe−λx=1,2,3,…
- E(X)=D(X)=λE(X)=D(X)=\lambdaE(X)=D(X)=λ
-
指数分布
X∼E(λ)∼Γ(1,λ)X\sim E(\lambda)\sim\Gamma(1,\lambda)X∼E(λ)∼Γ(1,λ)
- f(x)={λe−λx,x>00,x≤0f(x)=\begin{cases}\lambda e^{-\lambda x},&x>0\\0,&x\le0\end{cases}f(x)={λe−λx,0,x>0x≤0
- E(X)=1λE(X)=\frac{1}{\lambda}E(X)=λ1
- D(X)=1λ2D(X)=\frac1{\lambda^2}D(X)=λ21
-
伽马分布
X∼Γ(α,λ)X\sim\Gamma(\alpha,\lambda)X∼Γ(α,λ)
-
f(x)={xα−1Γ(α)λαe−λx,x>00,x≤0,α>0,λ>0f(x)=\begin{cases}\frac{ x^{\alpha-1}}{\Gamma(\alpha)} \lambda^\alpha e^{-\lambda x},&x>0\\0,&x\le0\end{cases},\ \alpha>0, \lambda >0f(x)={Γ(α)xα−1λαe−λx,0,x>0x≤0, α>0,λ>0
其中,Γ(α)=∫0+∞xα−1e−xdx\Gamma(\alpha)=\int_0^{+\infty}x^{\alpha-1}e^{-x}dxΓ(α)=∫0+∞xα−1e−xdx
-
E(X)=αλ,E(X2)=α(α+1)λ2E(X)=\frac{\alpha}{\lambda},\ E(X^2)=\frac{\alpha(\alpha+1)}{\lambda^2}E(X)=λα, E(X2)=λ2α(α+1)
-
D(X)=αλ2D(X)=\frac{\alpha}{\lambda^2}D(X)=λ2α
-
若Y∼Γ(α′,λ)Y\sim\Gamma(\alpha',\lambda)Y∼Γ(α′,λ)则X+Y∼Γ(α+α′,λ)X+Y\sim\Gamma(\alpha+\alpha', \lambda)X+Y∼Γ(α+α′,λ)
-
α=1\alpha=1α=1则伽马分布退化为指数分布
-
-
卡方分布
Xi∼N(0,1)X_i\sim N(0,1)Xi∼N(0,1)则:
χ2=∑i=1nXi∼χ2(n)\chi^2=\sum\limits_{i=1}^nX_i\sim\chi^2(n)χ2=i=1∑nXi∼χ2(n)(标准正态分布的和)
性质、定理:- E(χ2)=n,D(χ2)=2nE(\chi^2)=n, D(\chi^2)=2nE(χ2)=n,D(χ2)=2n
- X∼χ(n1),Y∼χ(n2)⇒X+Y∼χ2(n1+n2)X\sim\chi(n_1),Y\sim\chi(n_2)\Rightarrow X+Y\sim\chi^2(n_1+n_2)X∼χ(n1),Y∼χ(n2)⇒X+Y∼χ2(n1+n2)
- X∼E(λ)⇒2λX∼χ2(2)X\sim E(\lambda)\Rightarrow 2\lambda X\sim\chi^2(2)X∼E(λ)⇒2λX∼χ2(2) p10
-
t分布
X∼N(0,1),Y∼χ2(n)X\sim N(0,1), Y\sim\chi^2(n)X∼N(0,1),Y∼χ2(n),则:
T=XY/nT=\frac{X}{\sqrt{Y/n}}T=Y/nX(标准正态分布比根号卡方分布) -
F分布
X∼χ2(m),Y∼χ2(n)X\sim\chi^2(m), Y\sim\chi^2(n)X∼χ2(m),Y∼χ2(n)则:
F=X/mY/n∼F(m,n)F=\frac{X/m}{Y/n}\sim F(m,n)F=Y/nX/m∼F(m,n)(卡方分布的比)
性质:- F∼F(m,n)⇒1F∼F(n,m)F\sim F(m,n)\Rightarrow \frac{1}{F}\sim F(n,m)F∼F(m,n)⇒F1∼F(n,m)
- Fα(m,n)=1F1−α(n,m)F_{\alpha}(m,n)=\frac{1}{F_{1-\alpha}(n,m)}Fα(m,n)=F1−α(n,m)1
抽样分布定理
-
X∼N(μ,σ2)X\sim N(\mu,\sigma^2)X∼N(μ,σ2),则
- X‾∼N(μ,σ2n)\overline X\sim N(\mu,\frac{\sigma^2}{n})X∼N(μ,nσ2)
- (n−1)S2σ2∼χ2(n−1)\frac{(n-1)S^2}{\sigma^2}\sim\chi^2(n-1)σ2(n−1)S2∼χ2(n−1)
- X‾Sn∼t(n−1)\frac{\overline X}{\frac{S}{\sqrt n}}\sim t(n-1)nSX∼t(n−1)
- 样本均值和样本方差独立
-
X∼N(μ1,σ12),Y∼N(μ2,σ22)X\sim N(\mu_1,\sigma^2_1), Y\sim N(\mu_2, \sigma_2^2)X∼N(μ1,σ12),Y∼N(μ2,σ22),则
- (X‾−Y‾)−(μ1−μ2)σ12m+σ22n∼N(0,1)\frac{(\overline X-\overline Y)-(\mu_1-\mu_2)}{\sqrt{\frac{\sigma_1^2}{m}+\frac{\sigma_2^2}{n}}}\sim N(0,1)mσ12+nσ22(X−Y)−(μ1−μ2)∼N(0,1)
- SX2σ12/SY2σY2∼F(m−1,n−1)\frac{S_X^2}{\sigma_1^2}/\frac{S_Y^2}{\sigma_Y^2}\sim F(m-1,n-1)σ12SX2/σY2SY2∼F(m−1,n−1)
σ1=σ2\sigma_1=\sigma_2σ1=σ2时,有:
(X‾−Y‾)−(μ1−μ2)Sw1m+1n∼t(m+n−2)\frac{(\overline X-\overline Y)-(\mu_1-\mu_2)}{S_w\sqrt{\frac{1}{m}+\frac{1}{n}}}\sim t(m+n-2)Swm1+n1(X−Y)−(μ1−μ2)∼t(m+n−2)
其中Sw2=(m−1)SX2+(n−1)SY2m+n−2S_w^2=\frac{(m-1)S_X^2+(n-1)S_Y^2}{m+n-2}Sw2=m+n−2(m−1)SX2+(n−1)SY2
参数估计
估计的优良性
- Fisher信息量:I(θ)=E[∂∂θlnf(X;θ)]2I(\theta)=E[\frac{\partial}{\partial\theta}\ln f(X;\theta)]^2I(θ)=E[∂θ∂lnf(X;θ)]2
- 效率:e(θ^)=1nI(θ)D(θ^)e(\hat\theta)=\frac{1}{nI(\theta)D(\hat\theta)}e(θ^)=nI(θ)D(θ^)1
e(θ^)=1⇒θ^e(\hat\theta)=1\Rightarrow\hat\thetae(θ^)=1⇒θ^为有效估计量(克拉美-逻下界,D(θ^)=1nI(θ)D(\hat\theta)=\frac{1}{nI(\theta)}D(θ^)=nI(θ)1)
区间估计
已知总体X∼N(μ,σ2)X\sim N(\mu,\sigma^2)X∼N(μ,σ2),求1−α1-\alpha1−α置信区间
- 已知σ2=σ02\sigma^2=\sigma_0^2σ2=σ02,估计μ\muμ
(X‾−σ0nZα/2,X‾+σ0nZα/2)(\overline X-\frac{\sigma_0}{\sqrt n}Z_{\alpha/2},\overline X+\frac{\sigma_0}{\sqrt n}Z_{\alpha/2})(X−nσ0Zα/2,X+nσ0Zα/2)
- 总体方差未知,估计μ\muμ
(X‾−Sntα/2(n−1),X‾+Sntα/2(n−1))(\overline X-\frac{S}{\sqrt n}t_{\alpha/2}(n-1),\overline X+\frac{S}{\sqrt n}t_{\alpha/2}(n-1))(X−nStα/2(n−1),X+nStα/2(n−1))
- μ\muμ未知,估计σ2\sigma^2σ2
((n−1)S2χα/22(n−1),(n−1)S2χ1−α/22(n−1))(\frac{(n-1)S^2}{\chi^2_{\alpha/2}(n-1)}, \frac{(n-1)S^2}{\chi^2_{1-\alpha/2}(n-1)})(χα/22(n−1)(n−1)S2,χ1−α/22(n−1)(n−1)S2)
方差分析
单因素方差检验
-
H0:μ1=μ2=⋯=μkH_0:\mu_1=\mu_2=\dots=\mu_kH0:μ1=μ2=⋯=μk(不同水平对因素没有显著影响。该因素有k个水平,即k个类别)
-
SSA=∑i=1kni(Xi‾−X‾)2\text{SSA}=\sum\limits_{i=1}^kn_i(\overline{X_i}-\overline X)^2SSA=i=1∑kni(Xi−X)2(组间误差/组间平方和,每组均值减总均值的平方乘以组数量)
SSE=∑i=1k∑j=1nj(Xij−Xi‾)2\text{SSE}=\sum\limits_{i=1}^k\sum\limits_{j=1}^{n_j}(X_{ij}-\overline{X_i})^2SSE=i=1∑kj=1∑nj(Xij−Xi)2(组内误差/组内平方和,组内每一个值减该组均值求平方)
SST=∑i=1k∑j=1nj(Xij−X‾)2\text{SST}=\sum\limits_{i=1}^k\sum\limits_{j=1}^{n_j}(X_{ij}-\overline{X})^2SST=i=1∑kj=1∑nj(Xij−X)2(总平方和)
SST=SSA+SSE\text{SST}=\text{SSA}+\text{SSE}SST=SSA+SSE
检验量:F=SSA/(k−1)SSE/(N−k)∼F(k−1,N−k)F=\frac{\text{SSA}/(k-1)}{\text{SSE}/(N-k)}\sim F(k-1, N-k)F=SSE/(N−k)SSA/(k−1)∼F(k−1,N−k)(N是样本总数) -
方差分析表
方差来源 平方和 自由度 样本方差 F值 组间 SSA\text{SSA}SSA k−1k-1k−1 MSA=SSAk−1\text{MSA}=\frac{\text{SSA}}{k-1}MSA=k−1SSA F=MSAMSEF=\frac{\text{MSA}}{\text{MSE}}F=MSEMSA 组内 SSE\text{SSE}SSE N−kN-kN−k MSE=SSEN−k\text{MSE}=\frac{\text{SSE}}{N-k}MSE=N−kSSE 总和 SST\text{SST}SST N−1N-1N−1 -
MSE\text{MSE}MSE组内方差、均方差、均方
多重比较——最小显著差异法(LSD)
用于检验究竟是哪两个水平有显著差异
-
H0:μi=μjH_0:\mu_i=\mu_jH0:μi=μj
-
LSD=tα/2(n−k)⋅MSE⋅(1ni+1nj)\text{LSD}=t_{\alpha/2}(n-k)·\sqrt{\text{MSE}·(\frac{1}{n_i}+\frac{1}{n_j})}LSD=tα/2(n−k)⋅MSE⋅(ni1+nj1)(总共kkk个水平,现在检验水平iii和水平jjj)
若∣x‾i−x‾j∣>LSD|\overline x_i-\overline x_j|>\text{LSD}∣xi−xj∣>LSD则拒绝H0H_0H0
MSE计算方法见方差分析表
一元线性回归
-
β^1=n∑i=1nxiyi−∑i=1nxi∑i=1nyin∑i=1nxi2−(∑i=1nxi)2=∑i=1n(xi−x‾)(yi−y‾)∑i=1n(xi−x‾)2\hat\beta_1=\frac{n\sum\limits_{i=1}^nx_iy_i-\sum\limits_{i=1}^nx_i\sum\limits_{i=1}^ny_i}{n\sum\limits_{i=1}^nx^2_i-(\sum\limits_{i=1}^nx_i)^2}=\frac{\sum\limits_{i=1}^n(x_i-\overline x)(y_i-\overline y)}{\sum\limits_{i=1}^n(x_i-\overline x)^2}β^1=ni=1∑nxi2−(i=1∑nxi)2ni=1∑nxiyi−i=1∑nxii=1∑nyi=i=1∑n(xi−x)2i=1∑n(xi−x)(yi−y)
β^0=y‾−β^1x‾\hat\beta_0=\overline y-\hat\beta_1\overline xβ^0=y−β^1x
-
β^1\hat\beta_1β^1的显著性检验
- H0:β^1=0H_0: \hat\beta_1=0H0:β^1=0(两变量间的线性关系不显著)
- 检验统计量F=SSR/1SSE/(n−2)=MSRMSEF=\frac{\text{SSR}/1}{\text{SSE}/(n-2)}=\frac{\text{MSR}}{\text{MSE}}F=SSE/(n−2)SSR/1=MSEMSR
落入拒绝域⇒\Rightarrow⇒线性关系显著
-
SSR=∑(y^i−y‾)2\text{SSR}=\sum(\hat y_i-\overline y)^2SSR=∑(y^i−y)2(回归平方和)
SSE=∑(y^i−yi)2\text{SSE}=\sum(\hat y_i-y_i)^2SSE=∑(y^i−yi)2(残差平方和)
SST=∑(yi−y‾)2\text{SST}=\sum(y_i-\overline y)^2SST=∑(yi−y)2(总平方和/离差平方和) -
R2=SSRSST=1−SSESSTR^2=\frac{\text{SSR}}{\text{SST}}=1-\frac{\text{SSE}}{\text{SST}}R2=SSTSSR=1−SSTSSE(判定系数/拟合优度)
-
se=SSEn−2=MSEs_e=\sqrt{\frac{\text{SSE}}{n-2}}=\sqrt{\text{MSE}}se=n−2SSE=MSE(估计标准误差,《统计学》p250)
-
相关系数
-
公式
r=∑i=1n(Xi−X‾)(Yi−Y‾)∑i=1n(Xi−X‾)2⋅∑i=1n(Yi−Y‾)2=∑i=1nXiYi−nX‾⋅Y‾(∑i=1nXi2−nX‾2)⋅(∑i=1nYi2−nY‾2)r=\frac{\sum\limits_{i=1}^n(X_i-\overline X)(Y_i-\overline Y)}{\sqrt{\sum\limits_{i=1}^n(X_i-\overline X)^2·\sum\limits_{i=1}^n(Y_i-\overline Y)^2}}=\frac{\sum\limits_{i=1}^nX_iY_i-n\overline X·\overline Y}{\sqrt{(\sum\limits_{i=1}^nX_i^2-n\overline X^2)·(\sum\limits_{i=1}^nY_i^2-n\overline Y^2)}}r=i=1∑n(Xi−X)2⋅i=1∑n(Yi−Y)2i=1∑n(Xi−X)(Yi−Y)=(i=1∑nXi2−nX2)⋅(i=1∑nYi2−nY2)i=1∑nXiYi−nX⋅Y
-
显著性检验⇒\Rightarrow⇒《统计学》p240
- H0:ρ=0H_0: \rho=0H0:ρ=0(总体相关系数为0)
- t=∣r∣n−21−r2∼t(n−2)t=|r|\sqrt\frac{n-2}{1-r^2}\sim t(n-2)t=∣r∣1−r2n−2∼t(n−2)
-
-
回归方程区间估计(统计学 p256)
y^±tα/2(n−2)⋅se⋅1n+(x0−x‾)2∑i=1n(xi−x‾)2\hat y\pm t_{\alpha/2}(n-2)·s_e·\sqrt{\frac{1}{n}+\frac{(x_0-\overline x)^2}{\sum\limits_{i=1}^n(x_i-\overline x)^2}}y^±tα/2(n−2)⋅se⋅n1+i=1∑n(xi−x)2(x0−x)2
时间序列
- 增长率
- 环比:Gi=Yi−Yi−1Yi−1G_i=\frac{Y_i-Y_{i-1}}{Y_{i-1}}Gi=Yi−1Yi−Yi−1
- 定基:Gi=Yi−Y0Y0G_i=\frac{Y_i-Y_0}{Y_0}Gi=Y0Yi−Y0
- 平均:G‾=YnY0−1\overline G=\sqrt{\frac{Y_n}{Y_0}}-1G=Y0Yn−1
平稳序列
-
简单平均
Ft+1=1t∑i=1tYiF_{t+1}=\frac{1}{t}\sum\limits_{i=1}^tY_iFt+1=t1i=1∑tYi
-
移动平均
Ft+1=Y‾=1k∑i=0k−1Yt−iF_{t+1}=\overline Y=\frac{1}{k}\sum\limits_{i=0}^{k-1}Y_{t-i}Ft+1=Y=k1i=0∑k−1Yt−i
-
指数平滑
Ft+1=αYt+(1−α)Ft,F1=Y1F_{t+1}=\alpha Y_t+(1-\alpha)F_t,\quad F_1=Y_1Ft+1=αYt+(1−α)Ft,F1=Y1
相关文章:

应用统计部分常用公式总结
常见分布函数 常用公式 分位数:P{X>xα}α,P{X≤xα}1−αP\{X>x_\alpha\}\alpha, P\{X\le x_\alpha\}1-\alphaP{X>xα}α,P{X≤xα}1−αE(Xi)E(X)E(X‾)μE(X_i)E(X)E(\overline X)\muE(Xi)E(X)E(X)μE(X2)E2(X)D(X)μ2σ2E(X^2)E^2(X)D(X)\mu^2…...

阿赵的MaxScript学习笔记分享八《文件操作》
大家好,我是阿赵。继续分享MaxScript学习笔记第八篇 。这一篇主要讲文件操作,包括文件的I/O和导入导出。 1、获得3DsMax指定的一些目录路径 如果在电脑上安装了3DsMax软件,那么在文档里面会有一个3dsMax的文件夹,里面有一些3dsMa…...

将项目封装进docker进行迁移或使用
首先要理解docker的基本使用,本文不做过多阐述,博主也对docker没有了解透彻。 这里列一下docker的基本命令: docker info # 查看docker信息 docker -v # 查看docker版本 docker images # 查看docker所有的镜…...

matlab - 特殊矩阵、矩阵求值、稀疏矩阵
学习视频1.特殊矩阵1.1 通用特殊矩阵format % 零矩阵(全0) 幺矩阵(全1) 单位矩阵 % zeros ones eye rand(生成0~1的随机元素) randn(生成均值为1,方差为0的符合正太分布的随机阵)zeros(3) % 3x3的全0方阵 zeros(3, 4) % 3x4的全0矩阵 exA ones(3, 5) % 3x5的…...
Flume使用入门
目录 一. Flume简单介绍 1. Agent 2. Source 3. Sink 4. Channel 5. Event 二. 环境安装 1. 创建日志目录 2. 修改日志配置文件 3.修改运行堆内存 4. 确定日志打印的位置 5. 修改flume使用内存 内存调大 三. 校验flume 1. 安装netcat工具和net-tools工具 2. 判…...
【Servlet篇2】Servlet的工作过程,Servlet的api——HttpServletRequest
一、Servlet的工作过程 二、Tomcat的初始化 步骤1:寻找到当前目录下面所有需要加载的Servlet(也就是类) 步骤2:根据类加载的结果创建实例(通过反射),并且放入集合当中 步骤3:实例创建好之后,调用Servlet的init()方…...

【JAVASE】注解
文章目录1.概述2.JDK内置注解2.1override注解2.2 Deprecated注解3.元注解4.注解中定义属性4.1 属性value4.2 属性是一个数组5. 反射注解6.注解在开发中的作用1.概述 注解,也叫注释,是一种引用数据类型。编译后也同样生成class字节码文件。 语法 [修饰…...
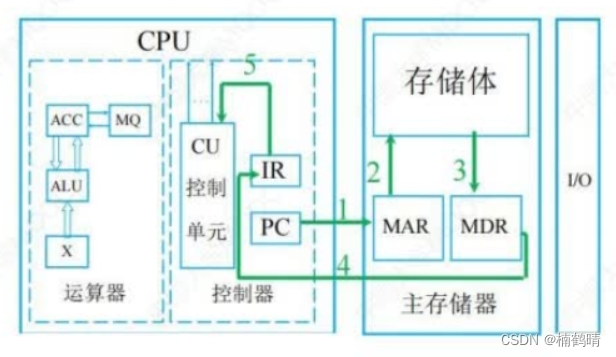
【408之计算机组成原理】计算机系统概述
目录前言一、计算机的发展历程1. 计算机发展的四代变化2. 计算机元件的更新换代3. 计算机软件的发展二、计算机系统层次结构1. 计算机系统的组成2. 冯诺依曼体系结构3. 计算机的功能部件1. 输入设备2. 输出设备3. 存储器4. 运算器5. 控制器三、 分析计算机各个部件在执行代码中…...
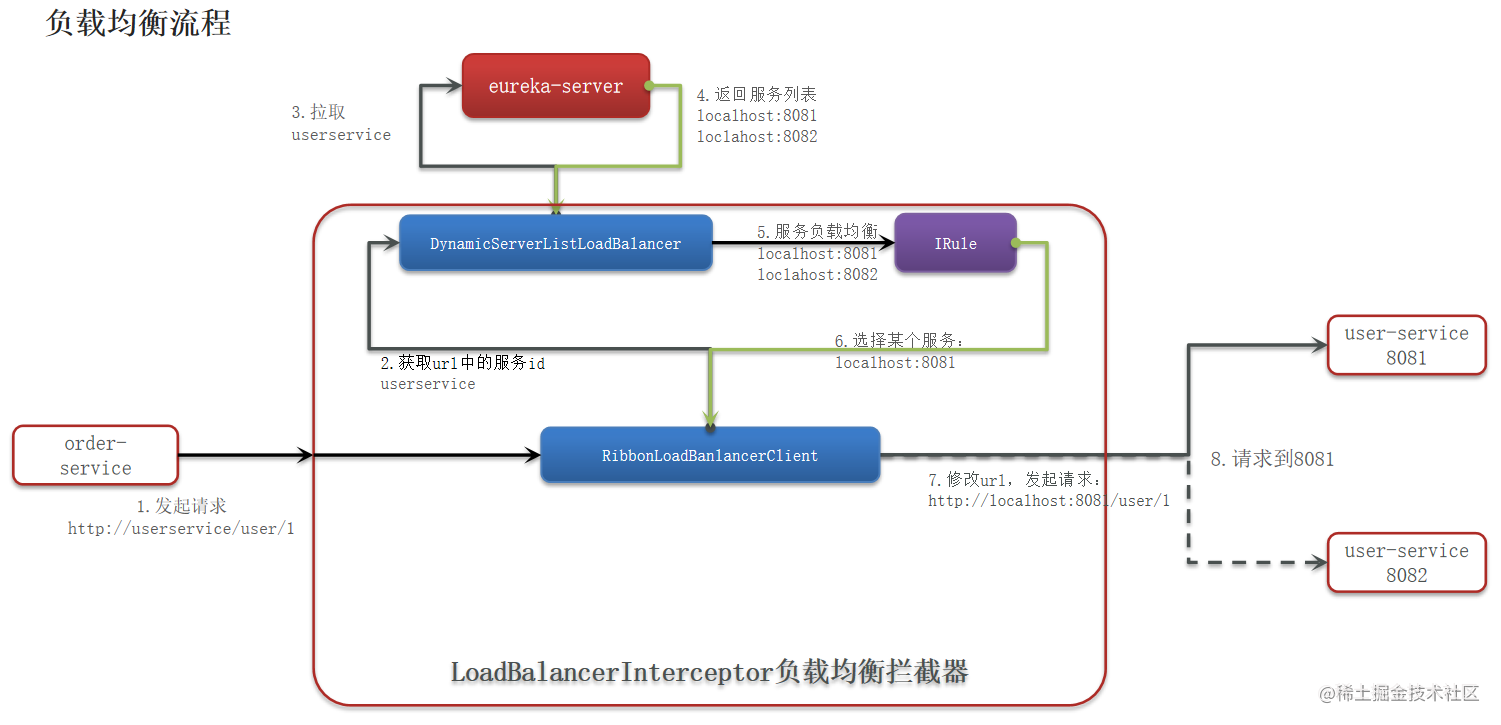
1.Spring Cloud (Hoxton.SR10) 学习笔记—基础知识
本文目录如下:一、Spring Cloud基础知识什么是微服务架构?服务拆分 有哪些注意事项?什么是分布式集群?分布式的 CAP 原则?组件 - Spring Cloud 哪几个组件比较重要?组件 - 为什么要使用这些组件?组件 - Na…...

嵌入式开发工具箱【持续更新中】【VMware、Ubuntutftp、nfs、SecureCRT、XShell、Source Insight 4.0】
一、概述 本文主要介绍嵌入式开发过程中需要用到的工具及简单的使用方法。避免在搭建嵌入式开发环境时,需要四处寻找文档,收藏此文章,一文搞定。 大多数嵌入式开发环境是使用Linux作为目标开发系统,所以开发主机一般都是Linux系统…...

深究Java Hibernate框架下的Deserialization
写在前面 Hibernate是一个开源免费的、基于 ORM 技术的 Java 持久化框架。通俗地说,Hibernate 是一个用来连接和操作数据库的 Java 框架,它最大的优点是使用了 ORM 技术。 Hibernate 支持几乎所有主流的关系型数据库,只要在配置文件中设置好…...
微服务一 实用篇 - Docker安装
《微服务一 实用篇 - Docker安装》 提示: 本材料只做个人学习参考,不作为系统的学习流程,请注意识别!!! 《微服务一 实用篇 - Docker安装》《微服务一 实用篇 - Docker安装》0.安装Docker1.CentOS安装Docker1.1.卸载(可选)1.2.安装docker1.3.启动docker…...

JavaSE22-集合2-map
文章目录一、集合概念二、map集合1、Map集合的特点2、HashMap2.1 HashMap特点2.2 创建对象2.3 常用方法2.4 遍历2.4.1 使用entrySet遍历2.4.2 使用keySet遍历3、HashMap的key去重原理一、集合概念 集合就是用于存储多个数据的容器。相对于具有相同功能的数组来说,集…...
【项目精选】病历管理系统设计与实现(源码+视频)
点击下载源码 企业财务管理系统主要用于电子病历来提高医院各项工作的效率和质量,促进医学科研、教学;减轻各类事务性工作的劳动强度,使他们腾出更多的精力和时间来服务于病人。本系统结构如下: 电子病例系统: 病人登…...
如何用Python把篮球和鸡联系起来
文章目录画个球让球转起来画个球 不管篮球和不和鸡联系起来,都首先得有个球,或者说要有一个球面,用参数方程可以表示为 xrcosϕcosθyrcosϕsinθzrsinϕ\begin{aligned} x & r\cos\phi\cos\theta\\ y & r\cos\phi\sin\th…...
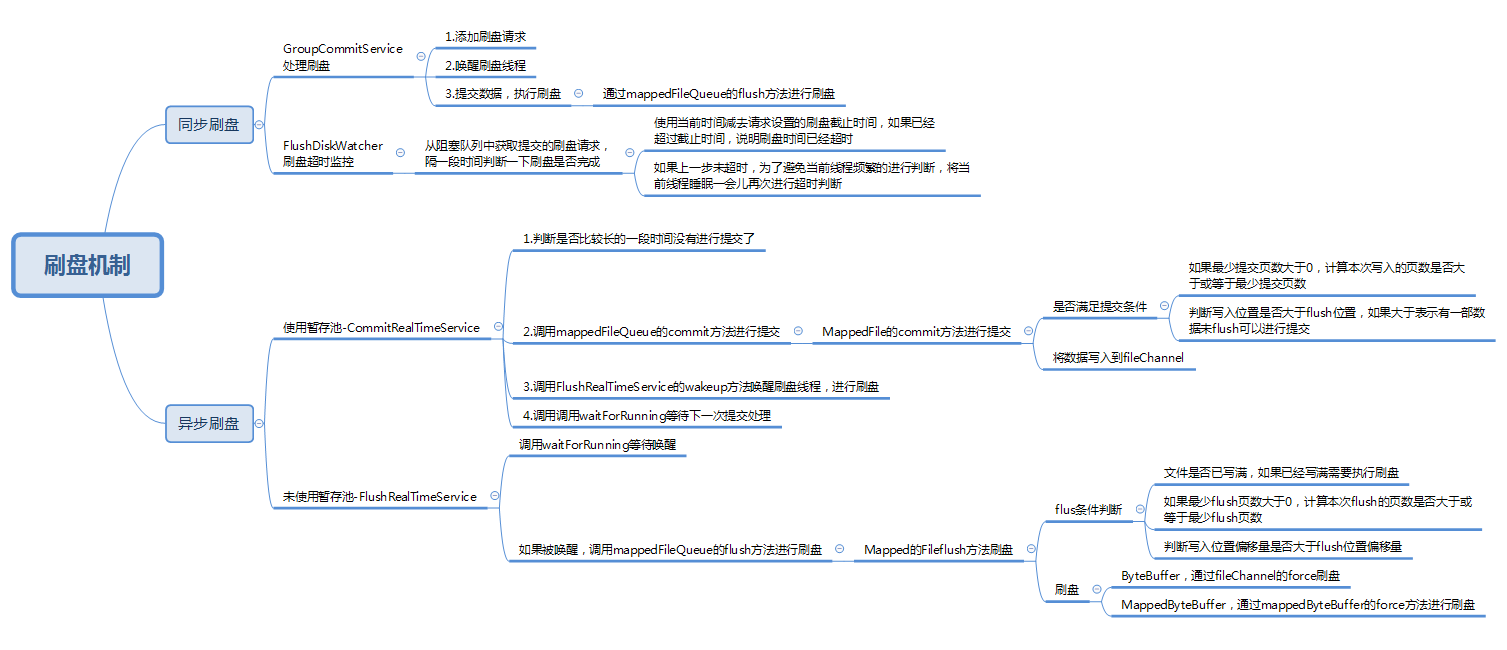
【RocketMQ】消息的刷盘机制
刷盘策略 CommitLog的asyncPutMessage方法中可以看到在写入消息之后,调用了submitFlushRequest方法执行刷盘策略: public class CommitLog {public CompletableFuture<PutMessageResult> asyncPutMessage(final MessageExtBrokerInner msg) {// …...

AMBA-AXI(一)burst 传输-INCR/WRAP/Fixed
💡Note:本文是根据AXI协议IHI0022F_b_amba_axi_protocol_spec.pdf(issue F)整理的。主要是分享AXI3.0和4.0部分。如果内容有问题请大家在评论区中指出,有补充或者疑问也可以发在评论区,互相学习ὤ…...
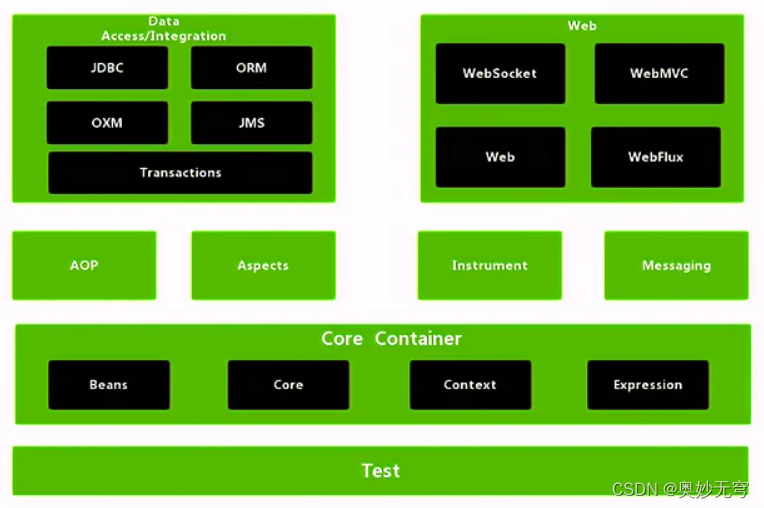
Java知识复习(八)Spring基础
1、什么是Spring框架? Spring :是一款开源的轻量级 Java 开发框架,旨在提高开发人员的开发效率以及系统的可维护性 2、Spring、SpringMVC和SpringBoot的区别 Spring主要指Spring Framework,就是指如上图所示的各项功能模块Spr…...

WuThreat身份安全云-TVD每日漏洞情报-2023-02-27
漏洞名称:OTFCC 缓冲区错误漏洞 漏洞级别:中危 漏洞编号:CVE-2022-35060,CNVD-2023-11996,CNNVD-202209-1527 相关涉及:OTFCC OTFCC 漏洞状态:EXP 参考链接:https://tvd.wuthreat.com/#/listDetail?TVD_IDTVD-2022-23648 漏洞名称:MuYucms 存在任意代码执行漏洞 漏洞级别:高危…...

上海交大陈海波教授、夏虞斌教授领衔巨作上市:《操作系统:原理与实现》
❤️作者主页:小虚竹 ❤️作者简介:大家好,我是小虚竹。2022年度博客之星评选TOP 10🏆,Java领域优质创作者🏆,CSDN博客专家🏆,华为云享专家🏆,掘金年度人气作…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...
