【C++干货铺】会搜索的二叉树(BSTree)
=========================================================================
个人主页点击直达:小白不是程序媛
C++系列专栏:C++干货铺
代码仓库:Gitee
=========================================================================
目录
前言:
二叉搜索树
二叉搜索树概念
二叉搜索树操作
二叉搜索树的查找
二叉搜索树的插入
二叉搜索树元素的删除
二叉搜索树的实现
BSTree结点
BSTree框架
拷贝构造函数和无参构造函数
析构函数
赋值重载(operator=)
插入Insert ()
查找Find()
删除()
中序遍历
二叉搜索树的应用
二叉搜索树的性能分析
前言:
在C语言的数据结构期间我们介绍过二叉树的一些概念;并且实现了其链式结构和实现了前、中、后序的遍历;有些OJ题使用C语言方式实现比较麻烦,比如有些地方要返回动态开辟的二维数组,非常麻烦。因此本节借二叉树搜索树,对二叉树部分进行收尾总结。并且后面的map和set特性需要先铺垫二叉搜索树,而二叉搜索树也是一种树形结构;二叉搜索树的特性了解,有助于更好的理解map和set的特性。
二叉搜索树
二叉搜索树概念
二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树:
- 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
- 若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
- 它的左右子树也分别为二叉搜索树

二叉搜索树操作
二叉搜索树的中序遍历根据其存储结构是排好序的。
- 如果左边存储比根小的数字右边存储比根大的数字,中序遍历的结果是升序的;
- 如果左边存储比根大的数组右边存储比根小的数字,中序遍历的结果是降序的;
int a[] = {8, 3, 1, 10, 6, 4, 7, 14, 13};
注意:二叉搜索树是没有“修改”的,因为如果随便修改一个数据,整棵树都要重新去实现。
二叉搜索树的查找
- 从根开始比较,查找,比根大则往右边走查找,比根小则往左边走查找。
- 最多查找高度次,走到空,还没找到,这个值不存在。
注意:
二叉搜索树有一个特别重要的特点:树中没有两个相同的元素。
二叉搜索树的插入
插入的具体过程如下:
- 树为空,则直接新增节点,赋值给root指针
- 树不空,按二叉搜索树性质查找插入位置,插入新节点

二叉搜索树元素的删除
首先查找元素是否在二叉搜索树中,如果不存在,则返回, 否则要删除的结点可能分下面四种情
况:
- 要删除的结点无孩子结点
- 要删除的结点只有左孩子结点
- 要删除的结点只有右孩子结点
- 要删除的结点有左、右孩子结点
看起来有待删除节点有4中情况,实际情况1可以与情况2或者3合并起来,因此真正的删除过程
如下:
- 情况b:删除该结点且使被删除节点的双亲结点指向被删除节点的左孩子结点--直接删除
- 情况c:删除该结点且使被删除节点的双亲结点指向被删除结点的右孩子结点--直接删除
- 情况d:在它的右子树中寻找中序下的第一个结点(关键码最小),用它的值填补到被删除节点中,再来处理该结点的删除问题--替换法删除
二叉搜索树的实现
BSTree结点
节点中包含两个该节点类型的指针,分别代表着指向左右孩子和节点中存储的值。
template <class K>
struct BSTNode
{BSTNode<K>* _left;BSTNode<K>* _right;K _key;//结点的构造函数BSTNode(const K& key):_left(nullptr), _right(nullptr), _key(key){}
};BSTree框架
成员变量为结点类型的指针。
template<class K>
class BST
{typedef BSTNode<K> Node;private:Node* _root=nullptr;
};拷贝构造函数和无参构造函数
因为我们自己写了拷贝构造函数,所以编译器不会默认生成无参构造函数。在C++11中可以让默认构造函数等于default,让编译器再次自动生成默认构造函数。
拷贝一个二叉搜索树开始要使用递归进行调用的。
BST() = default;BST(const BST<K>& st){_root=Copy(st._root);}析构函数
因为我们在类外面显示调用根节点很麻烦,直接在类内部以根节点为参数直接递归实现。
public:~BST(){Destory(_root);}
private:
void Destory(Node*& root){if (root == nullptr){return;}Destory(root->_left);Destory(root->_right);delete root;root = nullptr;}赋值重载(operator=)
swap函数是库std中的函数,深拷贝;
BST<K>& operator=(BST<K> t){swap(_root, t._root);return *this;}插入Insert ()
非递归版本
bool Insert(const K& key){if (_root == nullptr){_root = new Node(key);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){parent = cur;if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return false;}}cur = new Node(key);if (parent->_key < key){parent->_right = cur;}else if (parent->_key > key){parent->_left = cur;}}
- 首先还是要判断传入的根结点是否为空,如果为空直接开辟一个新的结点即可;
- 如果不为空,先创建一个父亲的结点便于插入的时候做修改;然后在创建一个结点从根节点开始根据二叉搜索树的特点开始找适合插入的位置,当找到时开辟一个新的结点,然后让合适位置的根节点指向开辟好的新节点即可;
递归版本
pbulic:bool InsertR(const K & key){return _InsertR(_root, key);}
private:
bool _InsertR(Node*& root,const K& key){if (root == nullptr){root = new Node(key);return true;}if (root->_key < key){return _InsertR(root->_right, key);}else if (root->_key > key){return _InsertR(root->_left, key);}else{return false;}}这里的递归也是根据二叉搜索树左右两边孩子的特点巧妙使用引用来实现的,每次递归的参数为上一个根节点指向左孩子或者右孩子的引用,去掉了记录父亲节点。
查找Find()
非递归版本
也是根据二叉搜索树左右孩子的特点实现的。如果查找的值比根结点的值大则和根节点的右孩子比较,反之;
注意:搜索二叉树中是没有两个相同的值的。
bool find(const K& key){if (_root == nullptr){return false;}Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return true;}}return false;}递归版本
public :bool FindR(const K & key){return _FindR(_root, key);}
private :bool _FindR(Node* root, const K& key){if (root == nullptr){return false;}if (root->_key < key){return _FindR(_root->_right, key);}else if (root->_key > key){return _FindR(root->_left, key);}else{return true;}}删除()
非递归版本
删除这里的情况还比较复杂,先要根据上面查找函数的思路找到结点;
- 如果左孩子为空,且该结点为父节点的左孩子,则让父节点指向的左孩子为该节点的右支;删掉此节点。如果该结点为父节点的右孩子,则让父节点指向的右孩子为该节点右支;删掉此节点。
- 如果右孩子为空,且该节点为父节点的左孩子,则让父节点指向的左孩子为该节点的右支;删掉此节点。如果该节点为父节点的右孩子,则让父节点指向的左孩子为该节点的左支;删掉此节点。
- 如果左右孩子都不为空,则要取左支最大的(最右结点)或者取右支最小的(最左结点),这里实现的是取右支最小的;先进入该结点的右边,然后使用循环找到最左结点;对该节点和其父节点的值进行交换,然后按照上面左孩子为空调整其父节点指向的孩子结点。然后删除结点。
bool Erase(const K& key){Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{//左为空if (cur->_left == nullptr){//删除根节点的值if (cur == _root){_root = cur->_right;}else{if (parent->_left == cur){parent->_left = cur->_right;}else if (parent->_right == cur){parent->_right = cur->_right;}}delete cur;}//右为空else if (cur->_right == nullptr){//删除根节点的值if (cur == _root){_root = cur->_left;}else{if (parent->_left == cur){parent->_left = cur->_left;}else if (parent->_right == cur){parent->_right = cur->_left;}}delete cur;}else{//右树的最小值Node* subleft = cur->_right;Node* parent = cur;while (subleft->_left){parent = subleft;subleft = subleft->_left;}swap(cur->_key, subleft->_key);if (subleft == parent->_left){parent->_left = subleft->_right;}else{parent->_right = subleft->_right;}delete subleft;}return true;}}return false;}递归版本
public:bool EraseR(const K&key){return _EraseR(_root, key);}
private:bool _EraseR(Node*& root, const K& key){if (root == nullptr){return false;}if (root->_key < key){return _EraseR(root->_right, key);}else if (root->_key > key){return _EraseR(root->_left, key);}else{if (root->_left == nullptr){Node* del = root;root = root->_right;delete del;return true;}else if (root->_right == nullptr){Node* del = root;root = root->_left;delete del;return true;}else{Node* subleft = root->_right;while (subleft->_left){subleft = subleft->_left;}swap(root->_key, subleft->_key);return _EraseR(root->_right, key);}}}中序遍历
public:void Inorder(){_Inorder(_root);cout << endl;}
private:
void _Inorder(Node* root){if (root == nullptr){return;}_Inorder(root->_left);cout << root->_key << " ";_Inorder(root->_right);}二叉搜索树的应用
1. K模型:K模型即只有key作为关键码,结构中只需要存储Key即可,关键码即为需要搜索到的值。
比如给一个单词word,判断该单词是否拼写正确,具体方式如下:
- 以词库中所有单词集合中的每个单词作为key,构建一棵二叉搜索树
- 在二叉搜索树中检索该单词是否存在,存在则拼写正确,不存在则拼写错误。
2. KV模型:每一个关键码key,都有与之对应的值Value,即<Key, Value>的键值对。该种方式在现实生活中非常常见:
- 比如英汉词典就是英文与中文的对应关系,通过英文可以快速找到与其对应的中文,英文单词与其对应的中文<word, chinese>就构成一种键值对;
- 再比如统计单词次数,统计成功后,给定单词就可快速找到其出现的次数,单词与其出现次数就是<word, count>就构成一种键值对。
二叉搜索树的性能分析
插入和删除操作都必须先查找,查找效率代表了二叉搜索树中各个操作的性能。
对有n个结点的二叉搜索树,若每个元素查找的概率相等,则二叉搜索树平均查找长度是结点在二
叉搜索树的深度的函数,即结点越深,则比较次数越多。但对于同一个关键码集合,如果各关键码插入的次序不同,可能得到不同结构的二叉搜索树:
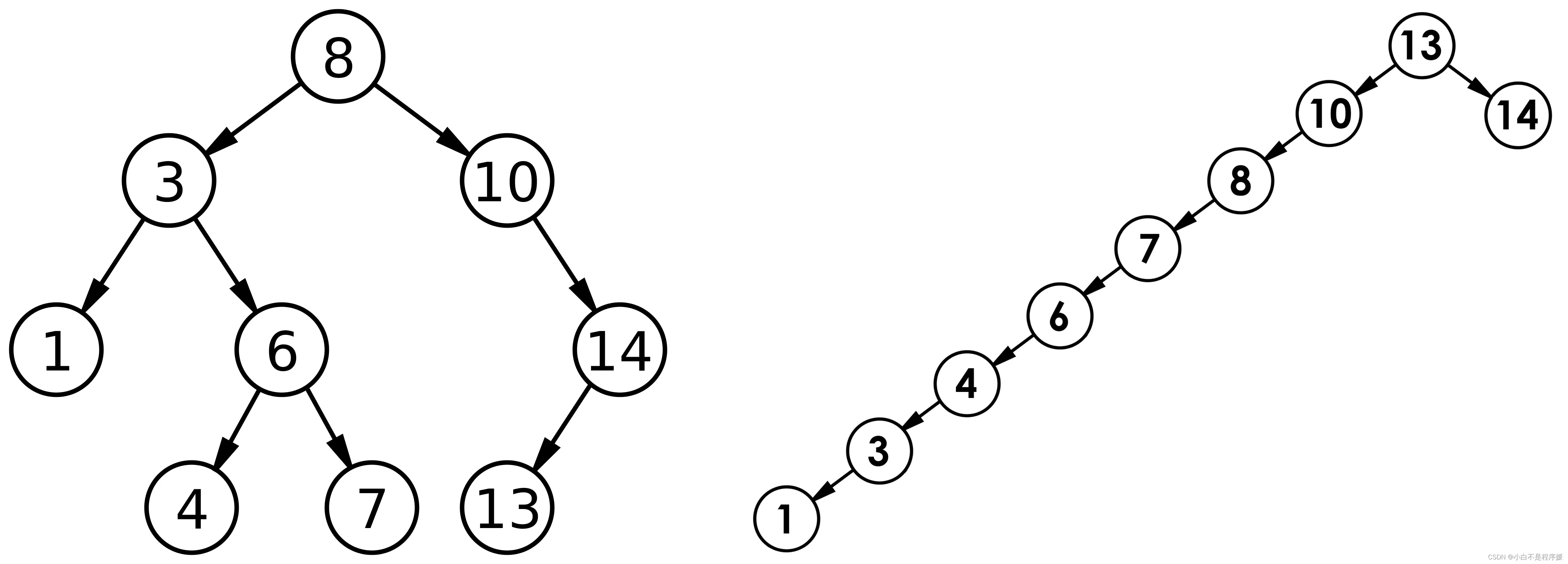
- 最优情况下,二叉搜索树为完全二叉树(或者接近完全二叉树),其平均比较次数为:O(logN)
- 最差情况下,二叉搜索树退化为单支树(或者类似单支),其平均比较次数为:O(N);如果退化成了单支树,那么二叉搜索树的性能就失去了。此时就需要用到即将登场的 AVL 树和红黑树了。
今天对二叉搜索树的介绍、使用、模拟实现的分享到这就结束了,希望大家读完后有很大的收获,也可以在评论区点评文章中的内容和分享自己的看法。您三连的支持就是我前进的动力,感谢大家的支持!! !
相关文章:

【C++干货铺】会搜索的二叉树(BSTree)
个人主页点击直达:小白不是程序媛 C系列专栏:C干货铺 代码仓库:Gitee 目录 前言: 二叉搜索树 二叉搜索树概念 二叉搜索树操作 二叉搜索树的查找 二叉搜索树的插入 二叉搜索树元素的删除 二叉搜索树的实现 BSTree结点 …...

【Spring AOP】 动态代理
一.AOP常见的实现方式 1.Spring AOP 2.aspectJ 注意:spring使用的是aspectJ的注解,但实现是spring自身实现的. 二.AOP原理 Spirng AOP原理 , 基于动态代理实现的. 三.代理模式 作用就是提供一个代理类,让我们在调用目标方法的时候,不再是直接对目标方法进行调用,而是通过代理类…...
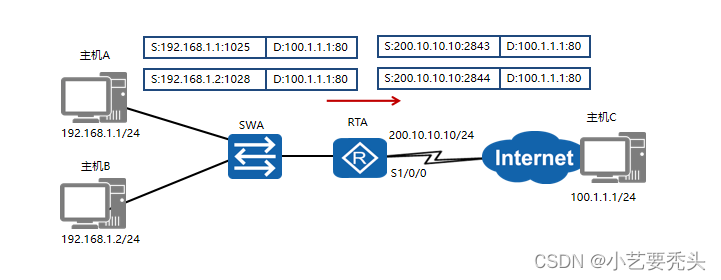
NAT——网络地址转换
目录 一、概念 二、NAT的分类 1.静态NAT 1.1 静态NAT的配置 1.2 利用eNSP小实验加强对静态NAT的理解 2、动态NAT 三、NAPT——端口映射 四、Easy IP 使用一个公网地址可以让所有人都上公网 一、概念 随着Internet的发展和网络应用的增多,IPv4地址枯竭已经成为…...

Lambda 表达式的常见用法
文章目录 Lambda 表达式的常见用法使用Lambda表达式集合遍历使用Lambda表达式排序使用Lambda表达式过滤使用Lambda表达式映射使用Lambda表达式归约使用Lambda表达式分组使用Lambda表达式函数式接口的实现使用Lambda表达式线程的创建使用Lambda表达式进行Optional 操作使用Lambd…...

成本管理常用的ChatGPT通用提示词模板
成本分析:如何进行成本分析? 成本核算:如何进行成本核算? 成本控制:如何控制成本? 成本效益分析:如何进行成本效益分析? 成本预测:如何预测成本? 成本决…...

如何在PHP中处理日期和时间?
在 PHP 中,你可以使用内置的 DateTime 类和相关函数来处理日期和时间。以下是一些常见的日期和时间操作的示例: 使用 DateTime 类: 获取当前日期和时间: $currentDateTime new DateTime(); echo $currentDateTime->format(Y-…...

NO-IOT翻频,什么是翻频,电信为什么翻频
1.1 翻频迁移最终的目的就是减少网络的相互干扰,提供使用质量. 1.2 随着与日俱增的网络规模的扩大,网内干扰已成了影响网络的质量标准之一,为了保障电信上网体验,满足用户日益增长的网速需求,更好的服务客户,电信针对…...

云原生之深入解析OOM和CPU节流
一、前言 使用 Kubernetes 时,内存不足 (OOM) 错误和 CPU 节流是云应用程序中资源处理的主要难题,这是为什么呢?云应用程序中的 CPU 和内存要求变得越来越重要,因为它们与云成本直接相关。通过 limits 和 requests ,可…...
)
数据结构与算法之递归: LeetCode 93. 复原 IP 地址 (Typescript版)
复原 IP 地址 https://leetcode.cn/problems/restore-ip-addresses/ 描述 有效 IP 地址 正好由四个整数(每个整数位于 0 到 255 之间组成,且不能含有前导 0),整数之间用 ‘.’ 分隔。 例如:“0.1.2.201” 和 “192.…...

json模块与jsonpath详解
数据提取之JSON与JsonPATH JSON(JavaScript Object Notation) 是一种轻量级的数据交换格式,它使得人们很容易的进行阅读和编写。同时也方便了机器进行解析和生成。适用于进行数据交互的场景,比如网站前台与后台之间的数据交互。 JSON和XML的比较可谓不…...

ubuntu20.04在noetic下编译orbslam2
ubuntu20.04在noetic下编译orbslam2 参考链接1:https://blog.csdn.net/qq_58869016/article/details/128660588 参考链接2:https://blog.csdn.net/dong123456789e/article/details/129693837 在noetic下的安装环境 1.库安装 sudo apt-get update sudo …...
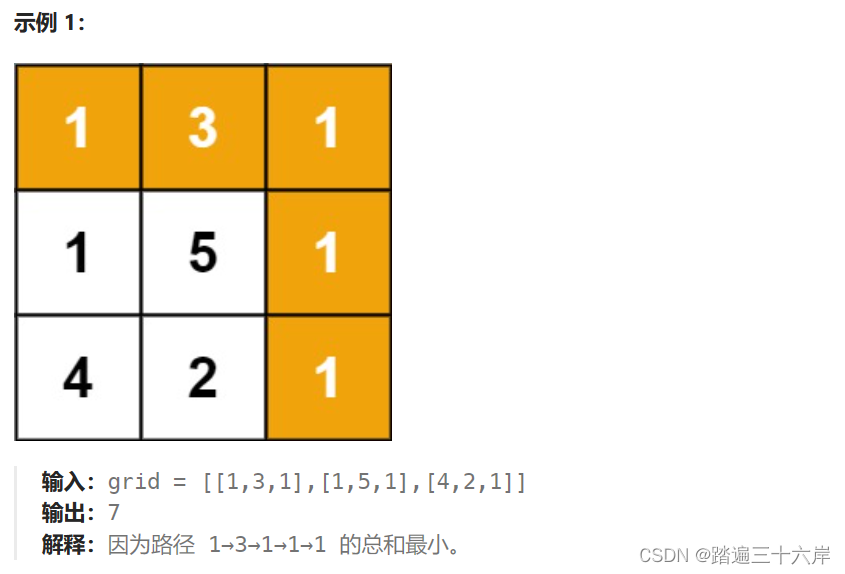
64. 最小路径和
最小路径和 描述 : 给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。 说明:每次只能向下或者向右移动一步。 题目 : LeetCode 64.最小路径和 64. 最小路径和 解析 : class So…...
)
惰性加载函数(js的问题)
在web开发中,因为浏览器之间的实现差异,一些嗅探工作总是不可避免。 var addEvent function( elem, type, handler ){if ( window.addEventListener ){return elem.addEventListener( type, handler, false );}if ( window.attachEvent ){return elem.…...
jmeter,读取CSV文件数据的循环控制
1、构造csv数据 保存文件时需要注意文件的编码格式 id,name,limit,status,address,start_time 100,小米100,1000,1,某某会展中心101,2023/8/20 14:20 101,小米101,1001,1,某某会展中心102,2023/8/21 14:20 2、在线程组下添加【CSV数据文件设置】元件 3、CSV文件数据的循环控…...

移植LVGL到像素屏,从此玩转像素屏0门槛
硬件方面 先上渲染图 实物图 配置 主控:esp32 micro32 plus主频:240MhzFlash:8MPSRAM:2M 软件方面 众所周知,LVGL是一个十分优秀的图形框架,小到几百kb的单片机,大到Linux都可以运行。既然它…...
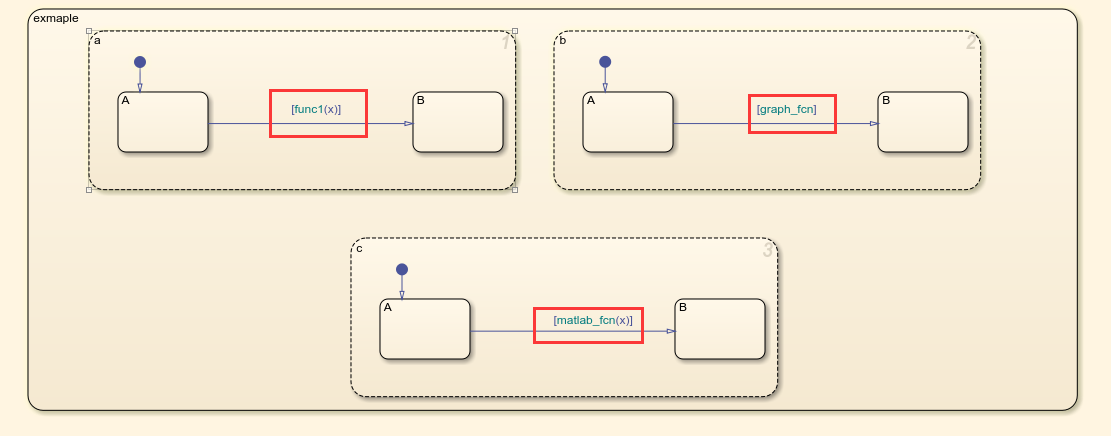
stateflow 之图函数、simulink函数和matlab函数使用及案例分析
目录 前言 1. 图函数graph function 2.simulink function 3.matlab function 4.调用stateflow中的几种函数方式 前言 对于stateflow实际上可以做simulink和matlab的所有任务,可以有matlab的m语言,也可以有simulink的模块,关于几种函数在…...

C# 加载本地文件设置应用程序图标
static class Program{[STAThread]static void Main(){Application.EnableVisualStyles();Application.SetCompatibleTextRenderingDefault(false);Form mainForm new Form1();mainForm.Show();//IntPtr hProcess Process.GetCurrentProcess().MainWindowHandle;// 设置应用程…...

苹果计划将全球1/4的IPhone产能转移至印度
KlipC报道:据相关人士报道,苹果希望在未来2到3年内每年在印度生产超过5000万部iphone,要是该计划得以实现,印度将占领全球iPhone产量的四分之一。 KlipC的分析师Alex Su表示:“此次iPhone15推出是苹果印度制造计划的一…...

el-date-picker 选择一个或多个日期
el-date-picker可选择多个日期 type“dates” 加个s即可 <div><span>el-date-picker选择多个日期</span><el-date-pickertype"dates"v-model"dateList"placeholder"选择一个或多个日期"></el-date-picker></di…...
5个创建在线帮助文档的好方法!
在线帮助文档是企业为用户提供支持服务的重要工具,它能够帮助用户更好地了解和使用产品,提高用户体验。然而,创建一份优秀的在线帮助文档需要掌握一定的技巧和方法。接下来就介绍一下创建在线帮助文档的5个好方法,帮助企业更好地为…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

