【字符串】leetcode28. 实现 strStr()(C/C++/Java/Python/Js)
leetcode28. 实现 strStr()
- 1 题目
- 2 KMP
- 2.1 什么是KMP?
- 2.2 KMP有什么用?
- 2.3 什么是前缀表?
- 2.4 最长公共前后缀
- 2.5 为什么一定要用前缀表?
- 2.6 如何计算前缀表
- 2.7 前缀表与next数组
- 2.8 使用next数组来匹配
- 2.9 时间复杂度分析
- 3 KMP代码思路
- 3.1 构造next数组
- 3.2 使用next数组来做匹配
- 4 代码
- 4.1 C++
- 4.2 C版本
- 4.3 Java版本
- 4.4 Python版本
- 4.5 JavaScript版本
- 5 总结:
在一个串中查找是否出现过另一个串,这是KMP的看家本领。
1 题目
题源链接
给你两个字符串 haystack 和 needle ,请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标(下标从 0 开始)。如果 needle 不是 haystack 的一部分,则返回 -1 。
示例 1:
输入:haystack = “sadbutsad”, needle = “sad”
输出:0
解释:“sad” 在下标 0 和 6 处匹配。
第一个匹配项的下标是 0 ,所以返回 0 。
示例 2:
输入:haystack = “leetcode”, needle = “leeto”
输出:-1
解释:“leeto” 没有在 “leetcode” 中出现,所以返回 -1 。
提示:
1 <= haystack.length, needle.length <= 104
haystack 和 needle 仅由小写英文字符组成
2 KMP
下面是Carl老师的视频讲解:
帮你把KMP算法学个通透!(理论篇)
帮你把KMP算法学个通透!(求next数组代码篇)
KMP的经典思想就是:当出现字符串不匹配时,可以记录一部分之前已经匹配的文本内容,利用这些信息避免从头再去做匹配。
2.1 什么是KMP?
为什么叫做KMP呢。
因为是由这三位学者发明的:Knuth,Morris和Pratt,所以取了三位学者名字的首字母。所以叫做KMP。
2.2 KMP有什么用?
KMP主要应用在字符串匹配上。
KMP的主要思想是当出现字符串不匹配时,可以知道一部分之前已经匹配的文本内容,可以利用这些信息避免从头再去做匹配了。
所以如何记录已经匹配的文本内容,是KMP的重点,也是next数组肩负的重任。
2.3 什么是前缀表?
next数组就是一个前缀表(prefix table)。
前缀表有什么作用呢?
前缀表是用来回退的,它记录了模式串与主串(文本串)不匹配的时候,模式串应该从哪里开始重新匹配。
为了清楚地了解前缀表的来历,我们来举一个例子:
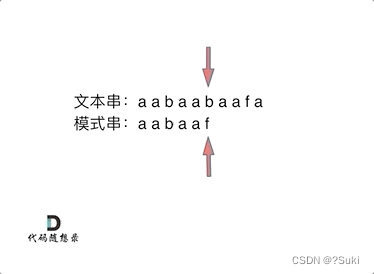
要在文本串:aabaabaafa 中查找是否出现过一个模式串:aabaaf。
请记住文本串和模式串的作用。
动画演示
文本串中第六个字符b 和 模式串的第六个字符f,不匹配了。如果暴力匹配,发现不匹配,此时就要从头匹配了。
但如果使用前缀表,就不会从头匹配,而是从上次已经匹配的内容开始匹配,找到了模式串中第三个字符b继续开始匹配。
前缀表是如何记录的呢?
前缀表的任务是当前位置匹配失败,找到之前已经匹配上的位置,再重新匹配,此也意味着在某个字符失配时,前缀表会告诉你下一步匹配中,模式串应该跳到哪个位置。
那么什么是前缀表:记录下标i之前(包括i)的字符串中,有多大长度的相同前缀后缀。
2.4 最长公共前后缀
字符串的前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串。
后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串。
可以将最长公共前后缀理解为最长相等前后缀,因为前缀表要求的就是相同前后缀的长度。
所以字符串a的最长相等前后缀为0。 字符串aa的最长相等前后缀为1。 字符串aaa的最长相等前后缀为2。 等等…
2.5 为什么一定要用前缀表?
刚刚匹配的过程在下标5的地方遇到不匹配,模式串是指向f,如图:

然后就找到了下标2,指向b,继续匹配:如图:
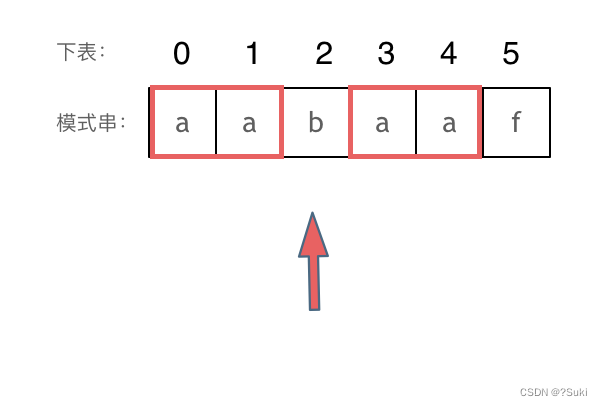
下标5之前这部分的字符串(也就是字符串aabaa)的最长相等的前缀 和 后缀字符串是 子字符串aa ,因为找到了最长相等的前缀和后缀,匹配失败的位置是后缀子串的后面,那么我们找到与其相同的前缀的后面重新匹配就可以了。
所以前缀表具有告诉我们当前位置匹配失败,跳到之前已经匹配过的地方的能力。
2.6 如何计算前缀表
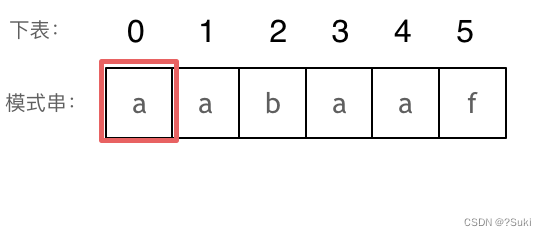
长度为前1个字符的子串a,最长相同前后缀的长度为0。(注意字符串的前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串;后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串。)
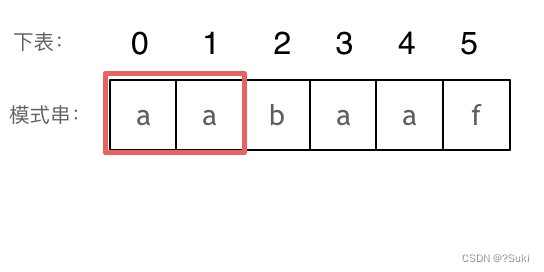
长度为前2个字符的子串aa,最长相同前后缀的长度为1。
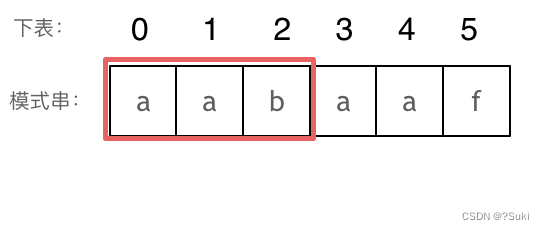
长度为前3个字符的子串aab,最长相同前后缀的长度为0。
以此类推: 长度为前4个字符的子串aaba,最长相同前后缀的长度为1。 长度为前5个字符的子串aabaa,最长相同前后缀的长度为2。 长度为前6个字符的子串aabaaf,最长相同前后缀的长度为0。
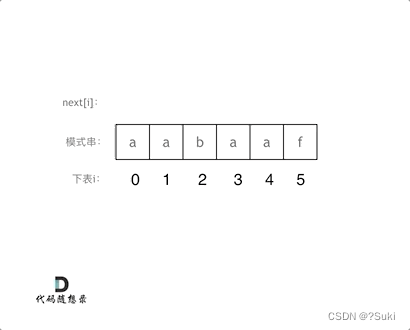
那么把求得的最长相同前后缀的长度就是对应前缀表的元素,如图:
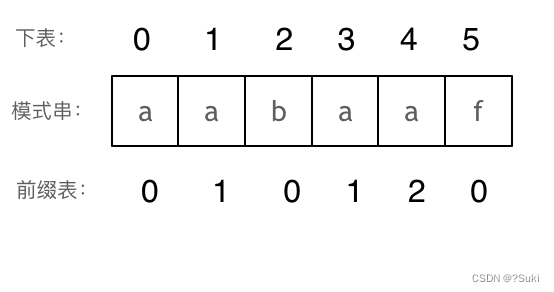
可以看出模式串与前缀表对应位置的数字表示的就是:下标i之前(包括i)的字符串中,有多大长度的相同前缀后缀。
再来看一下如何利用 前缀表找到 当字符不匹配的时候应该指针应该移动的位置。如动画所示:
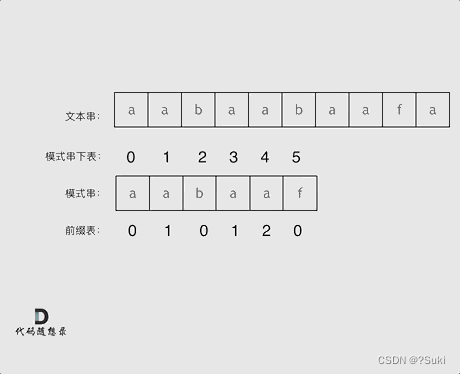
动画演示
找到的不匹配的位置, 那么此时我们要看它的前一个字符的前缀表的数值是多少。
因为要找前面字符串的最长相同的前缀和后缀。
所以要看前一位的 前缀表的数值。
前一个字符的前缀表的数值是2, 所以把下标移动到下标2的位置继续比配。 可以再反复看一下上面的动画。
最后就在文本串中找到了和模式串匹配的子串了。
2.7 前缀表与next数组
很多KMP算法的时间都是使用next数组来做回退操作,那么next数组与前缀表有什么关系呢?
next数组就可以是前缀表,但是很多实现都是把前缀表统一减一(右移一位,初始位置为-1)之后作为next数组。
其实这并不涉及到KMP的原理,而是具体实现,next数组既可以就是前缀表,也可以是前缀表统一减一(右移一位,初始位置为-1)。
2.8 使用next数组来匹配
以下我们以前缀表统一减一之后的next数组来做演示。
有了next数组,就可以根据next数组来 匹配文本串s,和模式串t了。
注意next数组是新前缀表(旧前缀表统一减一了)。
匹配过程动画如下:
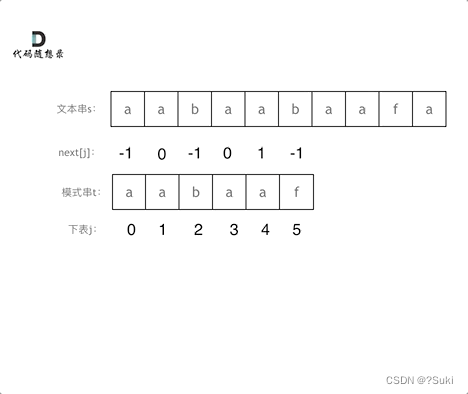
动画演示
2.9 时间复杂度分析
其中n为文本串长度,m为模式串长度,因为在匹配的过程中,根据前缀表不断调整匹配的位置,可以看出匹配的过程是O(n),之前还要单独生成next数组,时间复杂度是O(m)。所以整个KMP算法的时间复杂度是O(n+m)的。
暴力的解法显而易见是O(n × m),所以KMP在字符串匹配中极大地提高了搜索的效率。
3 KMP代码思路
3.1 构造next数组
定义一个函数getNext来构建next数组,函数参数为指向next数组的指针,和一个字符串。 代码如下:
void getNext(int* next, const string& s)
构造next数组其实就是计算模式串s,前缀表的过程。 主要有如下三步:
- 初始化
- 处理前后缀不相同的情况
- 处理前后缀相同的情况
1. 初始化:
定义两个指针i和j,j 指向前缀末尾位置,i 指向后缀末尾位置。
然后还要对next数组进行初始化赋值,如下:
j 为什么要初始化为 -1呢,因为之前说过 前缀表要统一减一的操作仅仅是其中的一种实现,我们这里选择j初始化为-1
next[i] 表示 i(包括i)之前最长相等的前后缀长度(其实就是j)
所以初始化next[0] = j 。
2. 处理前后缀不相同的情况
因为j初始化为-1,那么i就从1开始,进行s[i] 与 s[j+1]的比较。
所以遍历模式串s的循环下标i 要从 1开始,代码如下:
for (int i = 1; i < s.size(); i++) {
如果 s[i] 与 s[j+1]不相同,也就是遇到 前后缀末尾不相同的情况,就要向前回退。
next[j]就是记录着j(包括j)之前的子串的相同前后缀的长度。
那么 s[i] 与 s[j+1] 不相同,就要找 j+1前一个元素在next数组里的值(就是next[j])。
所以,处理前后缀不相同的情况代码如下:
while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了j = next[j]; // 向前回退
}
3. 处理前后缀相同的情况
如果 s[i] 与 s[j + 1] 相同,那么就同时向后移动i 和j 说明找到了相同的前后缀,同时还要将j(前缀的长度)赋给next[i], 因为next[i]要记录相同前后缀的长度。
代码如下:
if (s[i] == s[j + 1]) { // 找到相同的前后缀j++;
}
next[i] = j;
最后整体构建next数组的函数代码如下:
void getNext(int* next, const string& s){int j = -1;next[0] = j;for(int i = 1; i < s.size(); i++) { // 注意i从1开始while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了j = next[j]; // 向前回退}if (s[i] == s[j + 1]) { // 找到相同的前后缀j++;}next[i] = j; // 将j(前缀的长度)赋给next[i]}
}
代码构造next数组的逻辑流程动画如下:
动画演示
3.2 使用next数组来做匹配
在文本串s里 找是否出现过模式串t。
定义两个下标j 指向模式串起始位置,i指向文本串起始位置。
那么j初始值依然为-1,为什么呢? 依然因为next数组里记录的起始位置为-1。
i就从0开始,遍历文本串,代码如下:
for (int i = 0; i < s.size(); i++)
接下来就是 s[i] 与 t[j + 1] (因为j从-1开始的) 进行比较。
如果 s[i] 与 t[j + 1] 不相同,j就要从next数组里寻找下一个匹配的位置。
代码如下:
while(j >= 0 && s[i] != t[j + 1]) {j = next[j];
}
如果j指向了模式串t的末尾,那么就说明模式串t完全匹配文本串s里的某个子串了。
本题要在文本串字符串中找出模式串出现的第一个位置 (从0开始),所以返回当前在文本串匹配模式串的位置i 减去 模式串的长度,就是文本串字符串中出现模式串的第一个位置。
使用next数组,用模式串匹配文本串的整体代码如下:
int j = -1; // 因为next数组里记录的起始位置为-1
for (int i = 0; i < s.size(); i++) { // 注意i就从0开始while(j >= 0 && s[i] != t[j + 1]) { // 不匹配j = next[j]; // j 寻找之前匹配的位置}if (s[i] == t[j + 1]) { // 匹配,j和i同时向后移动j++; // i的增加在for循环里}if (j == (t.size() - 1) ) { // 文本串s里出现了模式串treturn (i - t.size() + 1);}
}
4 代码
4.1 C++
class Solution {
public:void getNext(int* next, const string& s) {int j = -1;next[0] = j;for (int i = 1; i < s.size(); i++) {while (j >= 0 && s[i] != s[j + 1]) { //处理前后缀不相同j = next[j]; //向前回退}if (s[i] == s[j + 1]) { //找到相同的前后缀j++;}next[i] = j; //将j(前缀的长度)赋给next[i]}}int strStr(string haystack, string needle) {if (needle.size() == 0) return 0;int next[needle.size()];getNext(next, needle);int j = -1; for (int i = 0; i < haystack.size(); i++) {while (j >= 0 && haystack[i] != needle[j + 1]) //不匹配j = next[j]; //j 寻找之前匹配的位置if (haystack[i] == needle[j + 1]) //匹配,j和i同时后移j++; //i的增加在for里if (j == (needle.size() - 1) ) //文本串s里出现了模式串treturn (i - needle.size() + 1);}return -1;}
};
4.2 C版本
int strStr(char * haystack, char * needle){int hLen = strlen(haystack);int nLen = strlen(needle);int *next = (int *)malloc(nLen*sizeof(int));int j = -1;next[0] = j;//求next数组for (int i = 1; i < nLen; i++) {while (j >= 0 && needle[i] != needle[j+1]) {j = next[j];}if (needle[i] == needle[j + 1])j++;next[i] = j;}//匹配j = -1;for (int i = 0; i < hLen; i++) {while (j >= 0 && haystack[i] != needle[j+1])j = next[j];if (haystack[i] == needle[j+1])j++;if (j == nLen - 1)return (i - nLen + 1);}return -1;
}
4.3 Java版本
class Solution {public void getNext(int[] next, String s) {int j = -1;next[0] = j;for (int i = 1; i < s.length(); i++) {while (j >= 0 && s.charAt(i) != s.charAt(j + 1)) //处理不匹配的情况j = next[j];if (s.charAt(i) == s.charAt(j + 1)) //处理匹配的情况,j和i都向后移j++; //i的增加在for里next[i] = j;}}public int strStr(String haystack, String needle) {if (needle.length() == 0) return 0;int [] next = new int[needle.length()];getNext(next, needle);int j = -1;for (int i = 0; i < haystack.length(); i++) {while (j >= 0 && haystack.charAt(i) != needle.charAt(j + 1) )j = next[j];if (haystack.charAt(i) == needle.charAt(j + 1))j++;if(j == needle.length() - 1)return i - needle.length() + 1;}return -1;}
}
4.4 Python版本
class Solution:def strStr(self, haystack: str, needle: str) -> int:a = len(needle)b = len(haystack)if a == 0:return 0next = self.getnext(a,needle)p=-1for j in range(b):while p >= 0 and needle[p+1] != haystack[j]:p = next[p]if needle[p+1] == haystack[j]:p += 1if p == a-1:return j-a+1return -1def getnext(self,a,needle):next = ['' for i in range(a)]k = -1next[0] = kfor i in range(1, len(needle)):while (k > -1 and needle[k+1] != needle[i]):k = next[k]if needle[k+1] == needle[i]:k += 1next[i] = kreturn next
4.5 JavaScript版本
/*** @param {string} haystack* @param {string} needle* @return {number}*/
var strStr = function (haystack, needle) {if (needle.length === 0)return 0;const getNext = (needle) => {let next = [];let j = -1;next.push(j);for (let i = 1; i < needle.length; ++i) {while (j >= 0 && needle[i] !== needle[j + 1])j = next[j];if (needle[i] === needle[j + 1])j++;next.push(j);}return next;}let next = getNext(needle);let j = -1;for (let i = 0; i < haystack.length; ++i) {while (j >= 0 && haystack[i] !== needle[j + 1])j = next[j];if (haystack[i] === needle[j + 1])j++;if (j === needle.length - 1)return (i - needle.length + 1);}return -1;
};
5 总结:
在一个串中查找是否出现过另一个串,这是KMP的看家本领。
扩展知识点就是next数组还可以优化为nextval数组。这里不做过多介绍。往年408 数据结构与算法中会有考察到。
可以参考王道。
下面是Carl老师的视频讲解:
帮你把KMP算法学个通透!(理论篇)
帮你把KMP算法学个通透!(求next数组代码篇)
KMP的经典思想就是:当出现字符串不匹配时,可以记录一部分之前已经匹配的文本内容,利用这些信息避免从头再去做匹配。
By Suki 2023/3/2
相关文章:

【字符串】leetcode28. 实现 strStr()(C/C++/Java/Python/Js)
leetcode28. 实现 strStr() 1 题目2 KMP2.1 什么是KMP?2.2 KMP有什么用?2.3 什么是前缀表?2.4 最长公共前后缀2.5 为什么一定要用前缀表?2.6 如何计算前缀表2.7 前缀表与next数组2.8 使用next数组来匹配2.9…...

游戏开发是个“坑”,而且是个“天坑”
本文首发于CSDN公众号 作者 | 开发游戏的老王 责编 | 梦依丹 出品 | CSDN(ID:CSDNnews) 各位游戏开发者大家好,我是开发游戏的老王,一名游戏开发者同时也是一名高校游戏方向的主讲教师,从事游戏开发及相关教…...
)
剑指 Offer 64. 求 1 + 2 + … + n(java解题)
剑指 Offer 64. 求 1 2 … n(java解题)1. 题目2. 解题思路3. 数据类型功能函数总结4. java代码1. 题目 求 12…n ,要求不能使用乘除法、for、while、if、else、switch、case等关键字及条件判断语句(A?B:C)。 示例…...

2022 年度_职业项目总结_Java技术点归纳
Java技术点归纳目录概述需求:设计思路实现思路分析1.Structs 元工程改造2.个贷子系统开发3.架构的迭代开发,升级,部署,参考资料和推荐阅读Survive by day and develop by night. talk for import biz , show your perfect code,fu…...
【项目实战】32G的电脑启动IDEA一个后端服务要2min,谁忍的了?
一、背景 本人电脑性能一般,但是拥有着一台高性能的VDI(虚拟桌面基础架构),以下是具体的配置 二、问题描述 但是,即便是拥有这么高的性能,每次运行基于Dubbo微服务架构下的微服务都贼久,以下…...
)
接口自动化面试题汇总(持续更新)
在自动化测试过程中,你如何处理测试数据?你会使用哪些方法来生成测试数据? 在自动化测试过程中,测试数据对于测试的准确性和覆盖率至关重要,常见方法有: 1、使用真实的生产数据:使用真实的生产…...
SpringBoot实现静态资源映射,登录功能以及访问拦截验证——以黑马瑞吉外卖为例
目录 一、项目简介 二、设置静态资源访问路径 三、实现登录功能 四、拦截访问请求 本篇文章以黑马瑞吉外卖为例 一、项目简介 瑞吉外卖项目分为后台和前台系统,后台提供给管理人员使用,前台则是用户订餐使用 资源我们放在resources下 二、设置静态…...

PythonWeb Django PostgreSQL创建Web项目(三)
了解Django框架下如何配置数据库链接与创建模型和应用 使用Django创建web项目,首先需要了解生成的项目文件结构,以及对应文件功能用途方可开始web项目页面创建,下方先介绍文件功能,之后再配置数据库连接以及管理创建模型与应用&a…...

【Visual Studio】git提交代码时使用GPG
前言 下载安装GPG的过程省略,直接开始进行配置 0.visual studio 版本说明 其余版本未测试,但是应该也是可以的 1 获取GPG的密钥ID 1.1 window下可以打开Kleopatra查看生成好的密钥的密钥ID 1.2 也可以从命令行中获取 gpg --list-keys 红框位置,后16位就是密钥ID 2 配置.git…...
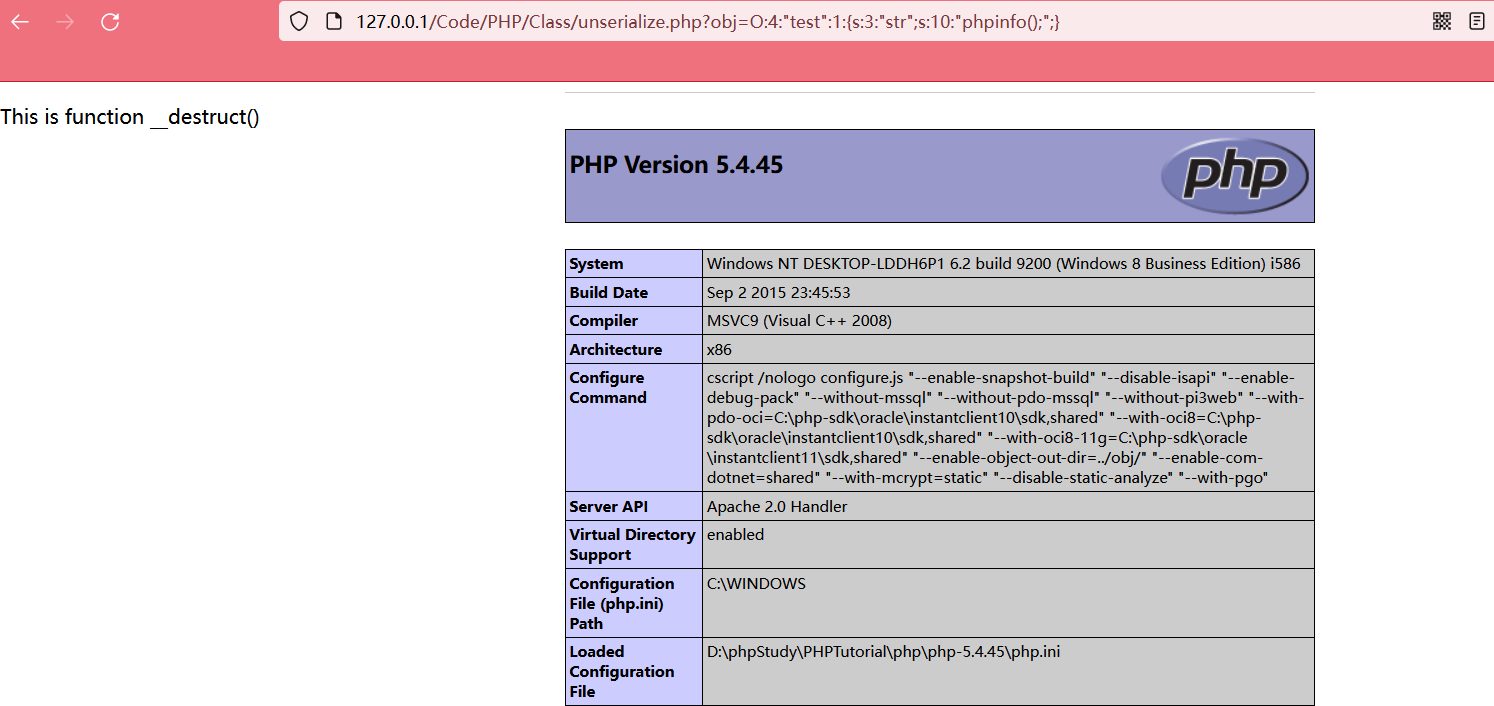
【反序列化漏洞-02】PHP反序列化漏洞实验详解
为什么要序列化百度百科上关于序列化的定义是,将对象的状态信息转换为可以存储或传输的形式(字符串)的过程。在序列化期间,对象将其当前状态写入到临时或持久性存储区(非关系型键值对形式的数据库Redis,与数组类似)。以后,可以通过…...

Gateway网关的使用
Gateway服务网关Spring Cloud Gateway 是 Spring Cloud 的一个全新项目,该项目是基于 Spring 5.0,Spring Boot 2.0 和 Project Reactor 等响应式编程和事件流技术开发的网关,它旨在为微服务架构提供一种简单有效的统一的 API 路由管理方式。1…...
【LeetCode】背包问题总结
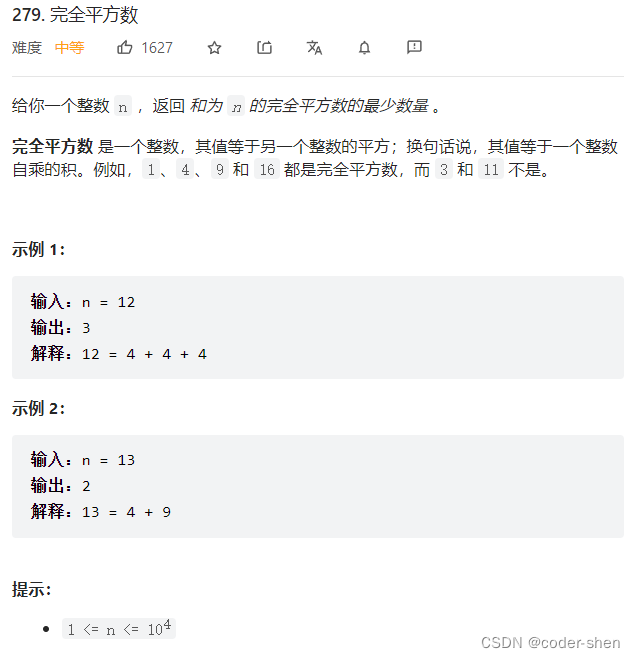
文章目录一、背包能否装满?416. 分割等和子集1049. 最后一块石头的重量 II二、装满背包有几种方法?494. 目标和518.零钱兑换II377. 组合总和 Ⅳ70. 爬楼梯三、背包装满的最大价值474.一和零四、装满背包最小物品数322. 零钱兑换279.完全平方数一、背包能…...

Java的开发工具有哪些?这十款工具大厂都在用!
工欲善其事必先利其器,各位同学大家好,我是小源~本期文章,给大家推荐十款Java的开发工具。一、 文本编辑器主要推荐三款:notepad、editplus、sublime text。这三款编辑工具,在我们的开发工作中几乎是相差无几ÿ…...

web学习-Node.js入门学习
web学习-Node.js入门学习1.回顾与思考2. 初识Node.js2.1 Node.js的简介2.2Node.js的环境安装2.3. fs文件系统模块2.3.1 fs.readFile()2.3.2 fs.writeFile()2.3.3 练习-整理考试成绩2.3.4 fs模块-路径动态拼接的问题2.4 path路径模块2.5 http模块2.5.1 服务器相关的概念2.5.2 创…...

100 eeeee
全部 答对 答错 敏捷综合训练3 1.看板中的精益生产概念是如何减少工作在瓶颈时期的影响? A它不会减少瓶颈,因为瓶颈是任何生产系统不可避免的副产品 B通过运用 5Y 分析根本原因 C通过成为一个及时的进度系统 D通过每周完善活动 答错了 收藏 学员得…...

物盾安全汤晓冬:工业互联网企业如何应对高发的供应链安全风险?
编者按:物盾安全是一家专注于物联网安全的产品厂商,其核心产品“物安盾”在能源、制造、交通等多个领域落地,为这些行业企业提供覆盖物联网云、管、边、端的安全整体解决方案。“物安盾”集成了腾讯安全制品扫描(BSCA)…...

微纳制造技术——基础知识
1.什么是直接带隙半导体和间接带隙半导体 导带底和价带顶处以同一K值,称为直接带隙半导体 导带底和价带顶不处在同一K值,称为间接带隙半导体 2.扩散和漂移的公式 3.三五族半导体的性质 1.high mobility 2.wide bandgap 3.direct bandgap 4.三五族…...

Makefile的使用
Makefile的使用 自动化编译脚本,这个东西就是,进行简单的设置,然后实现原码编成为相应程序,简单化自己进行相关操作的过程。不需要一个个自己进行全部进行输入。而且还有许多的简化书写方法。 这个Makefile的本质为一种脚本语言…...
RealBasicVSR模型转成ONNX以及用c++推理
文章目录安装RealBasicVSR的环境1. 新建一个conda环境2. 安装pytorch(官网上选择合适的版本)版本太低会有问题3. 安装 mim 和 mmcv-full4. 安装 mmedit下载RealBasicVSR源码下载模型文件写一个模型转换的脚步测试生成的模型安装RealBasicVSR的环境 1. 新建一个conda环境 cond…...
学习)
C语言作用域(变量生存的空间)学习
C 作用域规则 任何一种编程中,作用域是程序中定义的变量所存在的区域,超过该区域变量就不能被访问。C 语言中有三个地方可以声明变量: 在函数或块内部的局部变量 在所有函数外部的全局变量 在形式参数的函数参数定义中 让我们来看看什么是局…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...
