【LeetCode】背包问题总结
文章目录
- 一、背包能否装满?
- 416. 分割等和子集
- 1049. 最后一块石头的重量 II
- 二、装满背包有几种方法?
- 494. 目标和
- 518.零钱兑换II
- 377. 组合总和 Ⅳ
- 70. 爬楼梯
- 三、背包装满的最大价值
- 474.一和零
- 四、装满背包最小物品数
- 322. 零钱兑换
- 279.完全平方数
一、背包能否装满?
416. 分割等和子集

class Solution {
public:// 01背包:逆序遍历// 组合问题:先背包后容量bool canPartition(vector<int>& nums) {int m = nums.size();int sum = accumulate(nums.begin(), nums.end(), 0);if(sum & 1) return false;int n = sum / 2;vector<int> dp(n + 1, 0); // dp[j]:容量为j的背包,最多装入重量为dp[j]的物品for(int i = 0; i < m; i++){for(int j = n; j >= nums[i]; j--){dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);}}return dp[n] == n;}
};
dp背包问题——416. 分割等和子集
1049. 最后一块石头的重量 II

class Solution {
public:// 01背包:逆序遍历// 组合问题:先物品、后容量int lastStoneWeightII(vector<int>& stones) {int m = stones.size();int sum = accumulate(stones.begin(), stones.end(), 0);int n = sum / 2;vector<int> dp(n + 1, 0); // dp[j]:容量为j的背包,最多装dp[j]的石头for(int i = 0; i < m; i++){for(int j = n; j >= stones[i]; j--){dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);}}return sum - 2 * dp[n];}
};
dp背包问题——1049. 最后一块石头的重量 II
二、装满背包有几种方法?
494. 目标和

class Solution {
public:// 01背包:逆序遍历// 组合问题:先物品,后容量int findTargetSumWays(vector<int>& nums, int target) {int sum = accumulate(nums.begin(), nums.end(), 0);if((sum + target) & 1) return 0;int m = nums.size();int n = (sum + target) / 2;if(n < 0) return 0;vector<int> dp(n + 1, 0); // dp[j]:装满容量为j的背包,有dp[j]种方法dp[0] = 1; // 装满容量为0的背包,只有1种方法for(int i = 0; i < m; i++){for(int j = n; j >= nums[i]; j--){// 多了一个物品可选择后,装满背包的方法数就是 :(没有当前物品可选时的方法数 + 选了当前物品的方法数)dp[j] = dp[j] + dp[j - nums[i]];}}return dp[n];}
};
dp背包解决组合问题——494. 目标和
518.零钱兑换II

class Solution {
public:// 完全背包:顺序遍历// 组合问题:先物品、后容量int change(int amount, vector<int>& coins) {int m = coins.size();int n = amount;vector<int> dp(n + 1, 0); // dp[j]:装满容量为j的背包,有dp[j]种方式dp[0] = 1;for(int i = 0; i < m; i++){for(int j = coins[i]; j <= n; j++){// 多了一个物品可选后,装满背包的方法数就是 :(没有当前物品可选时的方法数 + 选了当前物品的方法数)dp[j] = dp[j] + dp[j - coins[i]];}}return dp[n];}
};
dp完全背包问题解组合问题——零钱兑换
377. 组合总和 Ⅳ

class Solution {
public:// 完全背包:顺序遍历// 排列问题:先容量,后物品int combinationSum4(vector<int>& nums, int target) {int m = nums.size();int n = target;vector<int> dp(n + 1, 0); // dp[j]:装满容量为j的背包,物品的组合数为dp[j]dp[0] = 1;for(int j = 1; j <= n; j++){for(int i = 0; i < m; i++){if(j >= nums[i] && dp[j] < INT_MAX - dp[j - nums[i]]) dp[j] += dp[j - nums[i]];}}return dp[n];}
};
70. 爬楼梯

class Solution {
public:// 完全背包:顺序遍历// 排列问题:先容量,后物品int climbStairs(int n) {int m = 2;int nums[2] = {1,2};vector<int> dp(n + 1, 0); // dp[j]:装满容量为j的背包,有dp[j]种方法dp[0] = 1;for(int j = 1; j <= n; j++){for(int i = 0; i < m; i++){if(j >= nums[i]) dp[j] = dp[j] + dp[j - nums[i]];}}return dp[n];}
};
排列问题:先容量,后物品
如果物品为{1,2},假如此时容量为2(容量为1的背包只能装物品1),用当前容量遍历多个物品,可以选择在装了物品1的基础上接着装,也可以选择不在其基础上装,直接装入物品2。当容量为3时,也可以选择在装有物品2的基础上再装入物品1,这样就出现了{2,1}
组合问题:先物品,后容量
如果物品为{1,2,3},假如此时容量为5

只有物品1,用各个容量遍历,此时无论是什么容量的背包,都只能放入物品1
此时我们手拿着物品2,对于每一个容量,要么直接使用现在就装满的背包,要么找一个剩余容量为2的背包放入当前物品2
接着我们手拿着物品3,对于每一个容量,要么直接使用现在就装满的背包,要么找一个剩余容量为3的背包放入当前物品3
class Solution {
public:int climbStairs(int n) {vector<int> dp(n + 1, 0);dp[0] = 1;dp[1] = 1;for(int i = 2; i <= n; i++){dp[i] = dp[i - 2] + dp[i - 1]; // 要么爬1个台阶,要么2个台阶}return dp[n];}
};
三、背包装满的最大价值
474.一和零

class Solution {
public:// 01背包:逆序遍历// 组合问题:先物品、后容量int findMaxForm(vector<string>& strs, int m, int n) {vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0)); // dp[i][j]:装满容量为ij背包的最大价值for(string& s : strs){int w0 = 0;int w1 = 0;for(char c : s){if(c == '0') w0++;else w1++;}// 每次循环计算出的dp[m][n]表示只有前几个物品可选时,所获得的最大价值for(int i = m; i >= w0; i--){for(int j = n; j >= w1; j--){dp[i][j] = max(dp[i][j], dp[i - w0][j - w1] + 1); // 1表示价值}}}return dp[m][n];}
};
四、装满背包最小物品数
322. 零钱兑换

class Solution {
public:// 问装满背包需要最少的物品数int coinChange(vector<int>& coins, int amount) {// 完全背包:顺序遍历// 组合问题:先物品、后容量,装满就行,不在意装入的顺序int m = coins.size();int n = amount;// 凑成面值n,最多需要n个硬币,初始化为n + 1即可vector<int> dp(n + 1, n + 1); // dp[j]:装满容量为j的背包至少需要dp[j]个物品dp[0] = 0;for(int i = 0; i < m; i++){for(int j = coins[i]; j <= n; j++){// 装满容量为j的背包,要么直接用前面的物品装满,要么找一个剩余容量为coins[i]的背包放入coins[i]dp[j] = min(dp[j], dp[j - coins[i]] + 1); }}return dp[n] == n + 1 ? -1 : dp[n];}
};
279.完全平方数
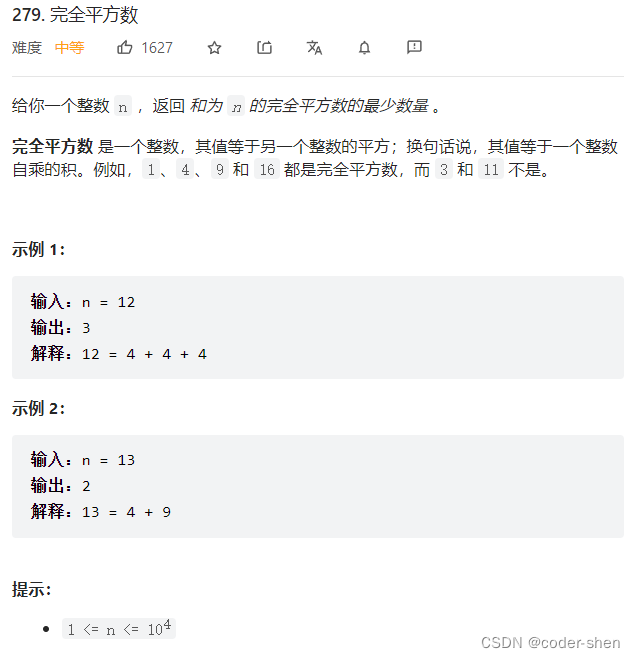
class Solution {
public:// 物品为:[1,4,9,...]// 容量为n,问装满背包至少需要几个物品int numSquares(int n) {// 完全背包:顺序遍历// 组合问题:先物品、后容量vector<int> dp(n + 1, n);dp[0] = 0;for(int i = 1; i <= n / i; i++){for(int j = i * i; j <= n; j++){dp[j] = min(dp[j], dp[j - i * i] + 1);}}return dp[n];}
};
相关文章:

【LeetCode】背包问题总结
文章目录一、背包能否装满?416. 分割等和子集1049. 最后一块石头的重量 II二、装满背包有几种方法?494. 目标和518.零钱兑换II377. 组合总和 Ⅳ70. 爬楼梯三、背包装满的最大价值474.一和零四、装满背包最小物品数322. 零钱兑换279.完全平方数一、背包能…...

Java的开发工具有哪些?这十款工具大厂都在用!
工欲善其事必先利其器,各位同学大家好,我是小源~本期文章,给大家推荐十款Java的开发工具。一、 文本编辑器主要推荐三款:notepad、editplus、sublime text。这三款编辑工具,在我们的开发工作中几乎是相差无几ÿ…...

web学习-Node.js入门学习
web学习-Node.js入门学习1.回顾与思考2. 初识Node.js2.1 Node.js的简介2.2Node.js的环境安装2.3. fs文件系统模块2.3.1 fs.readFile()2.3.2 fs.writeFile()2.3.3 练习-整理考试成绩2.3.4 fs模块-路径动态拼接的问题2.4 path路径模块2.5 http模块2.5.1 服务器相关的概念2.5.2 创…...

100 eeeee
全部 答对 答错 敏捷综合训练3 1.看板中的精益生产概念是如何减少工作在瓶颈时期的影响? A它不会减少瓶颈,因为瓶颈是任何生产系统不可避免的副产品 B通过运用 5Y 分析根本原因 C通过成为一个及时的进度系统 D通过每周完善活动 答错了 收藏 学员得…...

物盾安全汤晓冬:工业互联网企业如何应对高发的供应链安全风险?
编者按:物盾安全是一家专注于物联网安全的产品厂商,其核心产品“物安盾”在能源、制造、交通等多个领域落地,为这些行业企业提供覆盖物联网云、管、边、端的安全整体解决方案。“物安盾”集成了腾讯安全制品扫描(BSCA)…...

微纳制造技术——基础知识
1.什么是直接带隙半导体和间接带隙半导体 导带底和价带顶处以同一K值,称为直接带隙半导体 导带底和价带顶不处在同一K值,称为间接带隙半导体 2.扩散和漂移的公式 3.三五族半导体的性质 1.high mobility 2.wide bandgap 3.direct bandgap 4.三五族…...

Makefile的使用
Makefile的使用 自动化编译脚本,这个东西就是,进行简单的设置,然后实现原码编成为相应程序,简单化自己进行相关操作的过程。不需要一个个自己进行全部进行输入。而且还有许多的简化书写方法。 这个Makefile的本质为一种脚本语言…...
RealBasicVSR模型转成ONNX以及用c++推理
文章目录安装RealBasicVSR的环境1. 新建一个conda环境2. 安装pytorch(官网上选择合适的版本)版本太低会有问题3. 安装 mim 和 mmcv-full4. 安装 mmedit下载RealBasicVSR源码下载模型文件写一个模型转换的脚步测试生成的模型安装RealBasicVSR的环境 1. 新建一个conda环境 cond…...
学习)
C语言作用域(变量生存的空间)学习
C 作用域规则 任何一种编程中,作用域是程序中定义的变量所存在的区域,超过该区域变量就不能被访问。C 语言中有三个地方可以声明变量: 在函数或块内部的局部变量 在所有函数外部的全局变量 在形式参数的函数参数定义中 让我们来看看什么是局…...
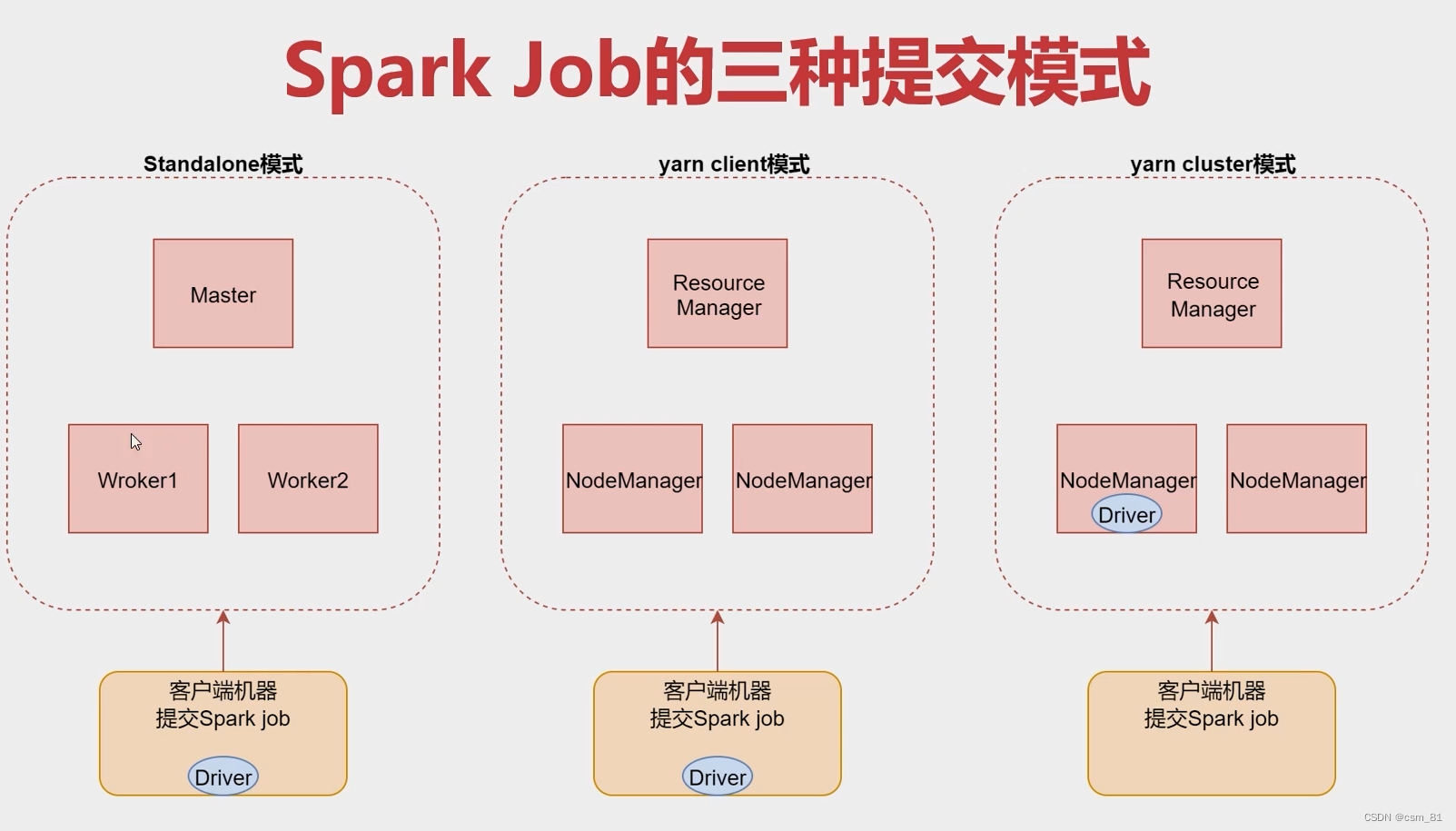
Spark性能优化一 概念篇
(一)宽依赖和窄依赖 窄依赖(Narrow Dependency):指父RDD的每个分区只被子RDD的一个分区所使用,例如map、filter等 这些算子一个RDD,对它的父RDD只有简单的一对一的关系,也就是说,RDD的每个part…...
[数据结构]:09-二分查找(顺序表指针实现形式)(C语言实现)
目录 前言 已完成内容 二分查找实现 01-开发环境 02-文件布局 03-代码 01-主函数 02-头文件 03-PSeqListFunction.cpp 04-SearchFunction.cpp 结语 前言 此专栏包含408考研数据结构全部内容,除其中使用到C引用外,全为C语言代码。使用C引用主要…...
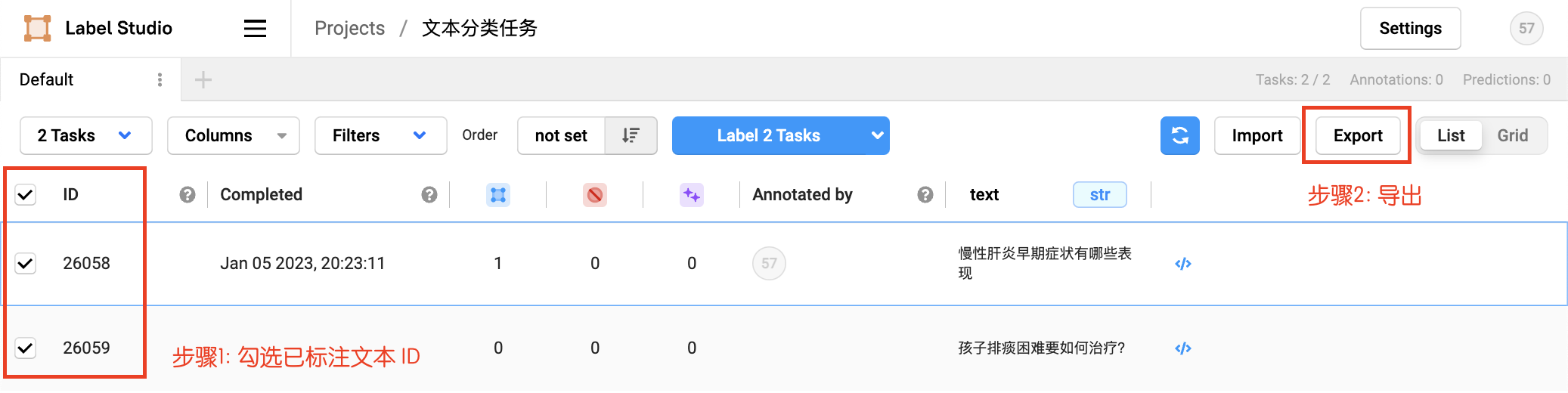
3.基于Label studio的训练数据标注指南:文本分类任务
文本分类任务Label Studio使用指南 1.基于Label studio的训练数据标注指南:信息抽取(实体关系抽取)、文本分类等 2.基于Label studio的训练数据标注指南:(智能文档)文档抽取任务、PDF、表格、图片抽取标注等…...
)
Python进阶-----面向对象3.0(面对对象三大特征之---封装)
目录 前言: 什么是封装 Python私有化封装 习题 前言: 上一期是讲解Python中类的私有属性和方法,其实很好理解,我给一个类中的部分属性进行加密拒绝访问(上一期链接Python进阶-----面向对象2.0&#…...

软考中级软件设计师备考建议
前言 首先我说一下个人对这个考试的一个感受看法,我觉得软件设计师考试并不难,主要是不要被内心的恐惧吓倒,考试中心态真的很重要! 一、中级软件设计师科目包括: (1)计算机与软件工程知识&am…...
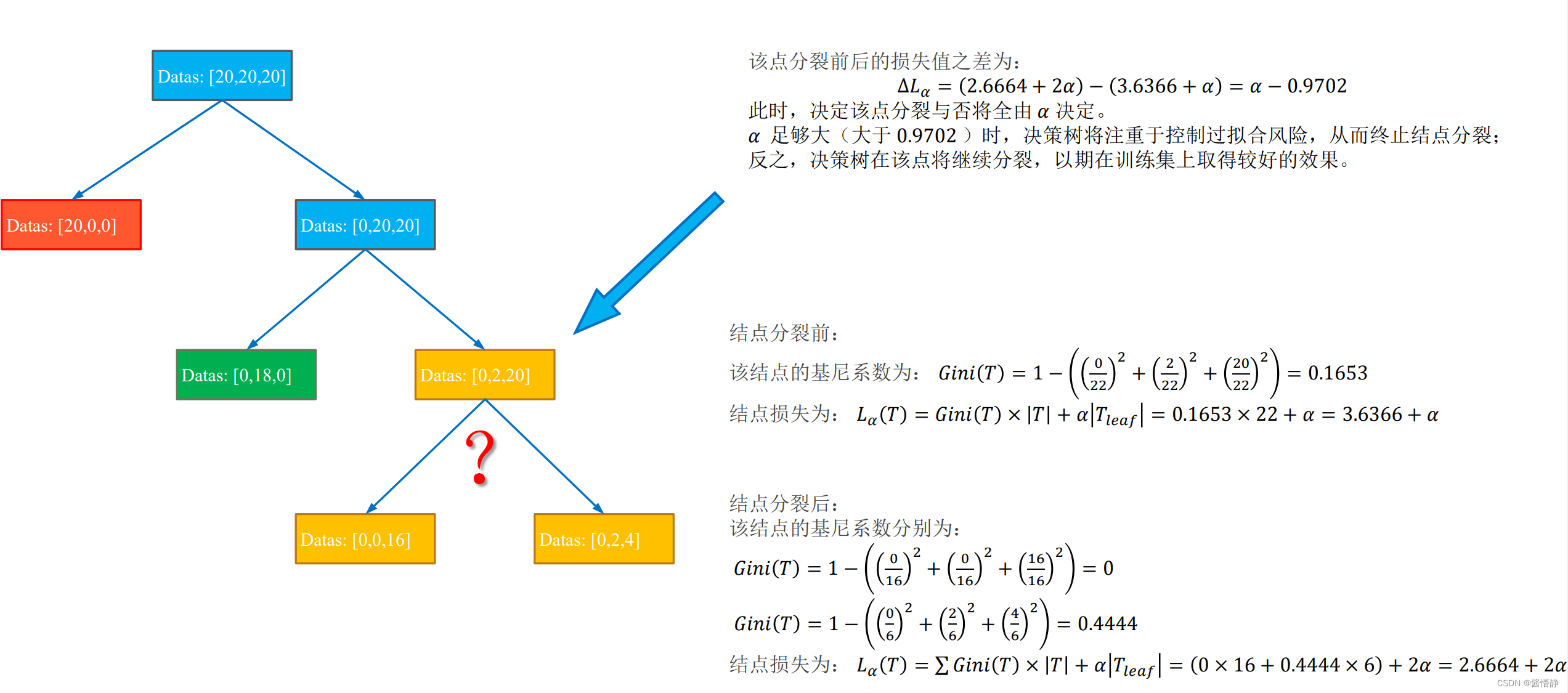
【机器学习】决策树(理论)
决策树(理论) 目录一、何为决策树1、决策树的组成2、决策树的构建二、熵1、熵的作用2、熵的定义3、熵的计算4、条件熵的引入5、条件熵的计算三、划分选择1、信息增益( ID3 算法选用的评估标准)2、信息增益率( C4.5 算法…...
VSCode下载与安装使用教程【超详细讲解】
目录 一、VSCode介绍 二、官方下载地址 三、VSCode安装 1、点击我同意此协议,点击下一步; 2、点击浏览,选择安装路径,点击下一步; 3、添加到开始菜单,点击下一步; 4、根据需要勾选&#…...

2023年3月北京/上海/广州/深圳DAMA数据管理认证CDGA/CDGP
弘博创新是DAMA中国授权的数据治理人才培养基地,贴合市场需求定制教学体系,采用行业资深名师授课,理论与实践案例相结合,快速全面提升个人/企业数据治理专业知识与实践经验,通过考试还能获得数据专业领域证书。 DAMA认…...

进程和线程理论知识
1.进程和线程之间的联系。 进程是程序依次执行的过程,线程是比进程小的执行单位。 一个进程在其执行过程中可以创建多个线程。 多个线程共享进程的堆和方法区内存资源。 进程是OS进行资源分配的基本单位。 线程是OS进行调度的基本单位。 进程和线程是1࿱…...

华为OD机试用Python实现 -【广播服务器】
华为OD机试题 最近更新的博客华为 OD 机试 300 题大纲广播服务器题目输入输出示例一输入输出示例二输入输出Python代码代码编写思路最近更新的博客 华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题...
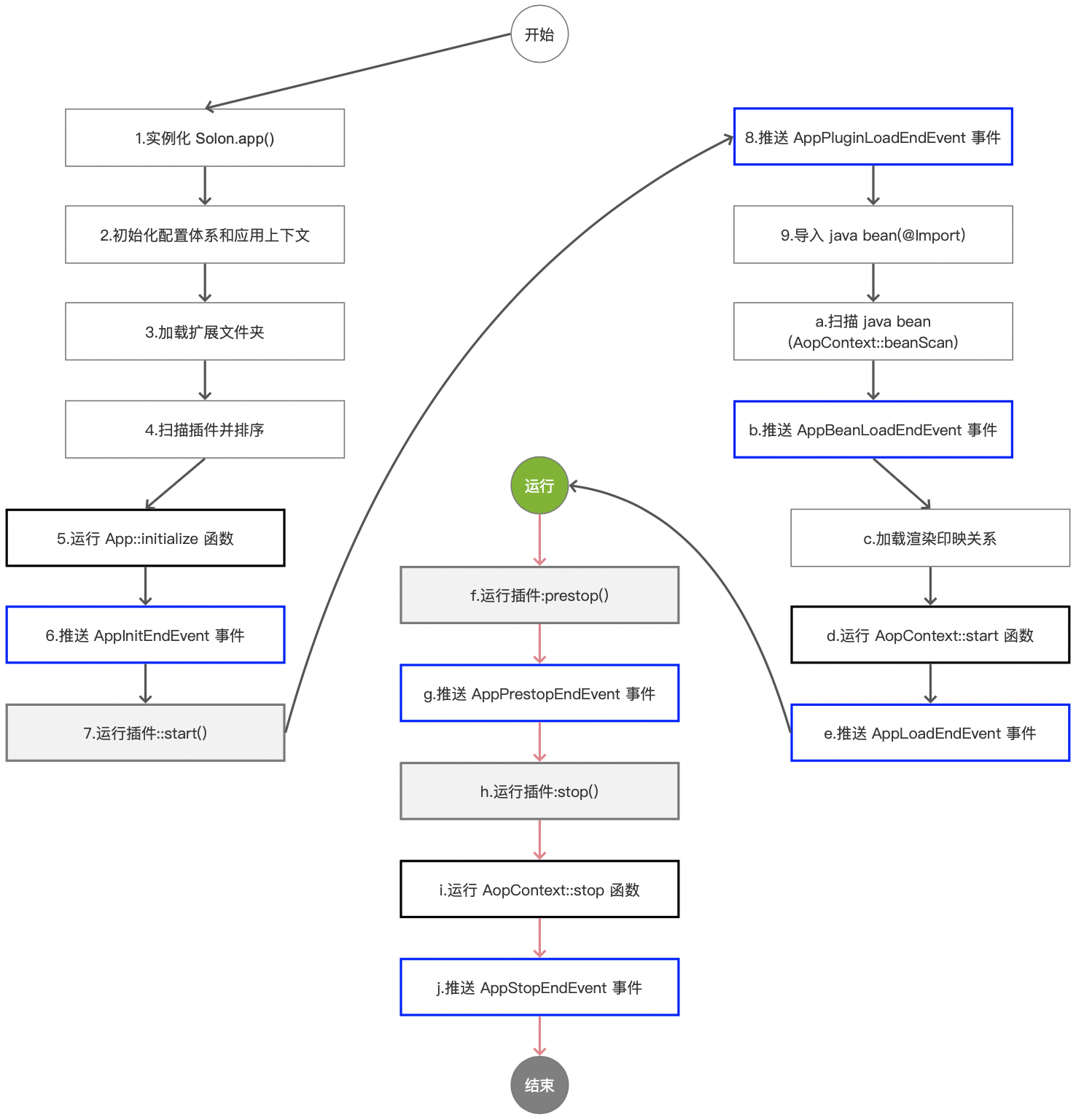
Solon2 的应用生命周期
Solon 框架的应用生命周期包括:一个初始化函数时机点 六个事件时机点 两个插件生命时机点 两个容器生命时机点(v2.2.0 版本的状态): 提醒: 启动过程完成后,项目才能正常运行(启动过程中&…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

【免费数据】2005-2019年我国272个地级市的旅游竞争力多指标数据(33个指标)
旅游业是一个城市的重要产业构成。旅游竞争力是一个城市竞争力的重要构成部分。一个城市的旅游竞争力反映了其在旅游市场竞争中的比较优势。 今日我们分享的是2005-2019年我国272个地级市的旅游竞争力多指标数据!该数据集源自2025年4月发表于《地理学报》的论文成果…...

文件上传漏洞防御全攻略
要全面防范文件上传漏洞,需构建多层防御体系,结合技术验证、存储隔离与权限控制: 🔒 一、基础防护层 前端校验(仅辅助) 通过JavaScript限制文件后缀名(白名单)和大小,提…...
