当前位置： 首页 > news >正文

数据结构和算法-最小生成树（prim和krusakal）和最短路径问题（BFS和dijkastra和floyd）

news 2025/10/14 9:08:51

文章目录

  • 最小生成树
    • 总览
    • 生成树
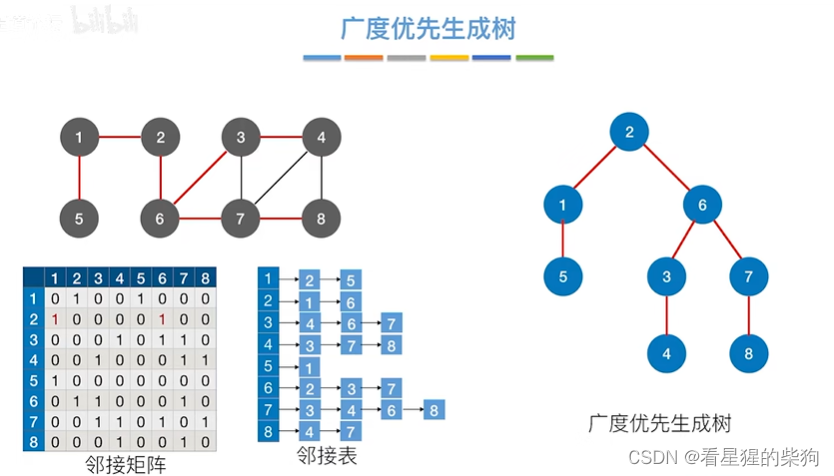
    • 广度优先生成树
    • 深度优先生成树
    • 最小生成树
    • Prim算法
    • Kruskal算法
    • Prim vs Krusakal
      • Prim的实现
      • Kruskal的实现
    • 小结
  • 最短路径问题
    • 单源最短路径问题
      • BFS求无权图的单源最短路径
      • 小结
      • Dijkastra算法
        • 算法时间复杂度
        • 不适用情况
    • 每一对顶点的最短路径问题
      • Floyd算法
        • 找两个点的最短路径
        • 核心代码
        • 实例
        • 找两个顶点最短路径
        • Floyd用于负权图
        • 不能解决的问题
      • 小结

最小生成树

总览

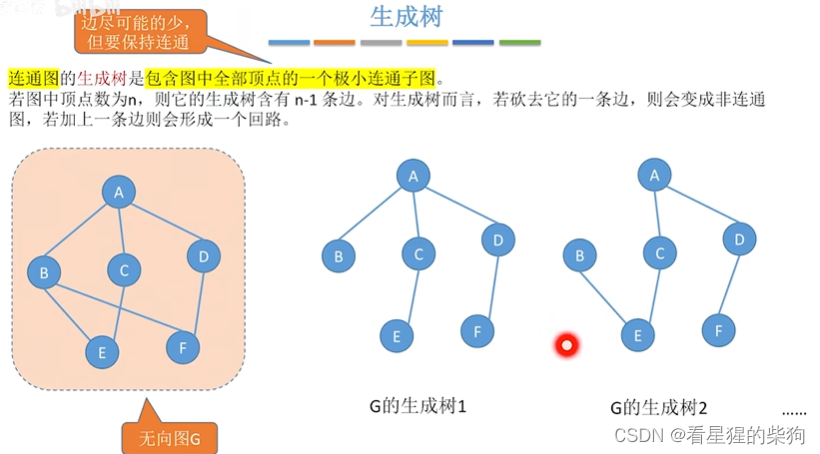
在这里插入图片描述

生成树

在这里插入图片描述

广度优先生成树

在这里插入图片描述

深度优先生成树

在这里插入图片描述

最小生成树

针对的是带权连通图
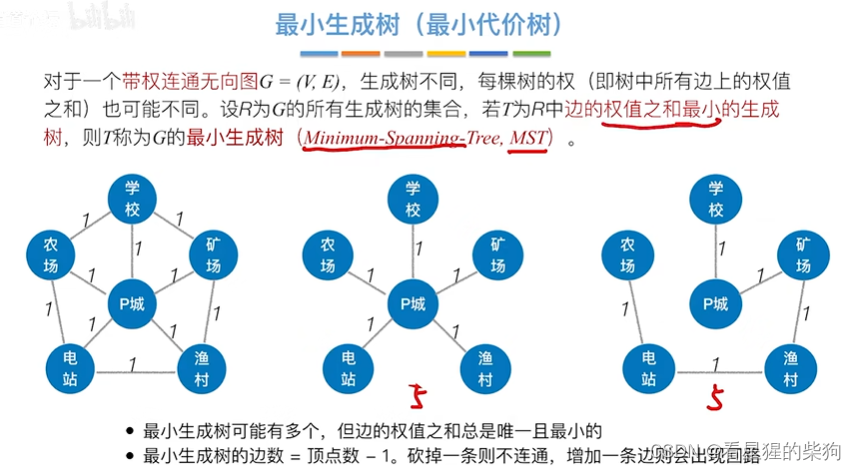
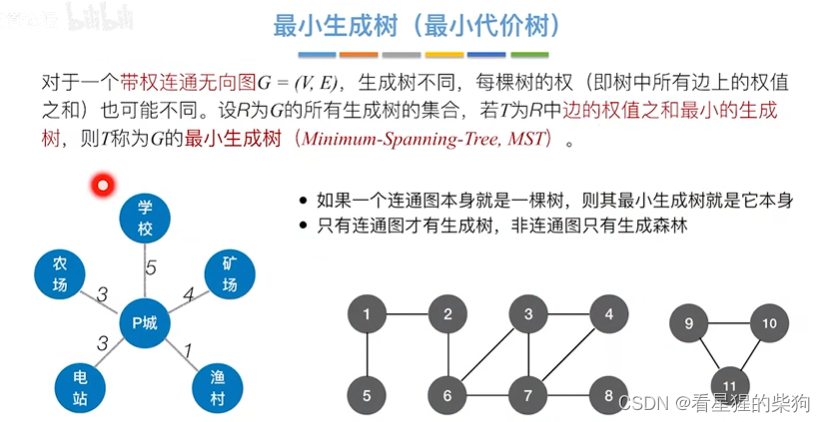
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

Prim算法

同一个图的最小生成树可能不唯一

从p城出发
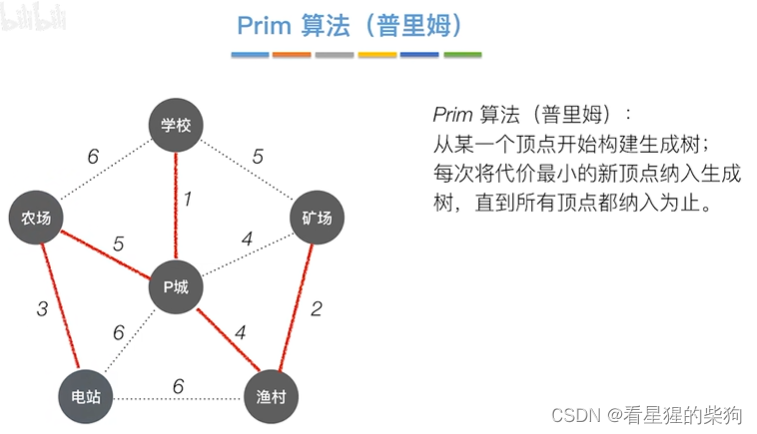
在这里插入图片描述
在这里插入图片描述

从农场出发也一样
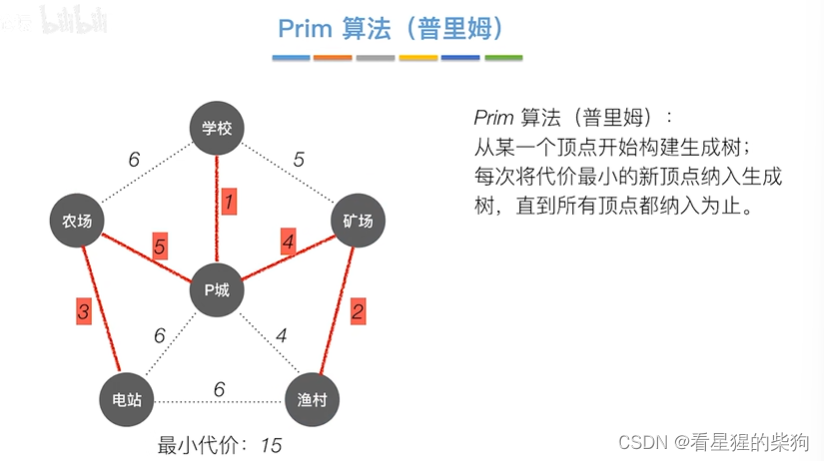
在这里插入图片描述

Kruskal算法

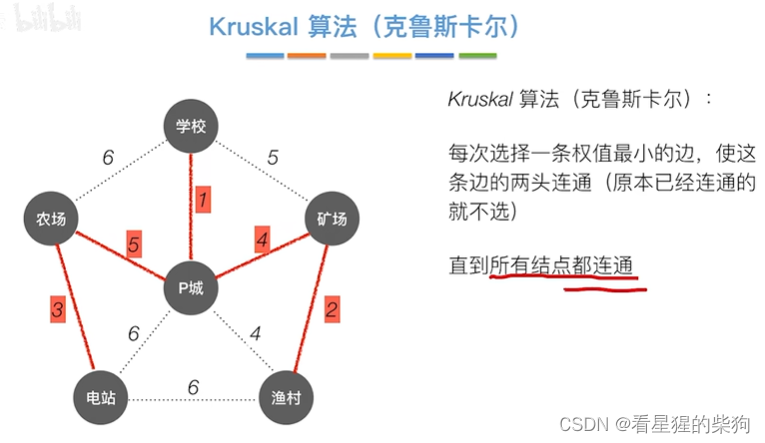
在这里插入图片描述

Prim vs Krusakal

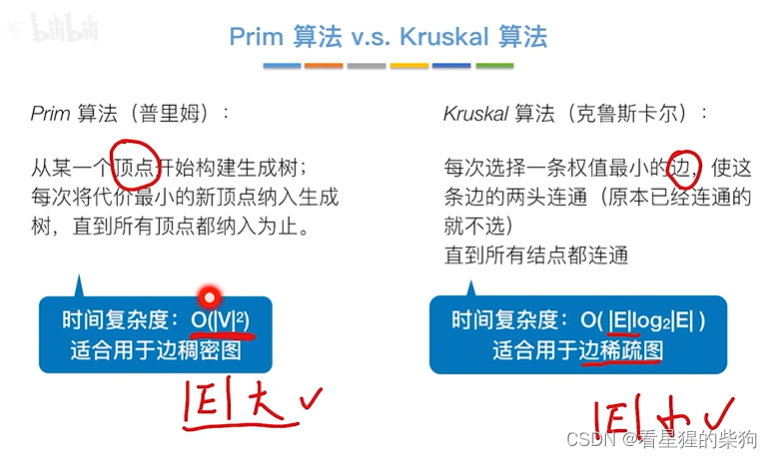
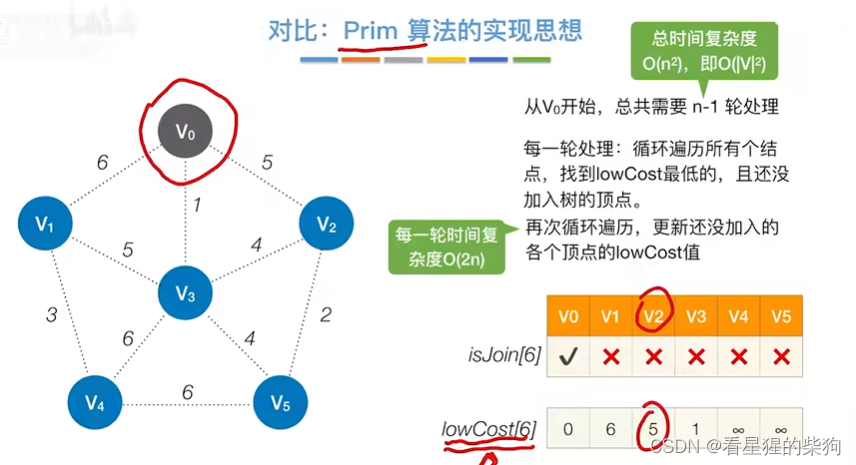
在这里插入图片描述

Prim的实现

先找到最低代价的节点，每次将节点加入树后，需要更新各节点加入树的最低代价（即将原来的代价和个节点与加入节点的代价作比较）
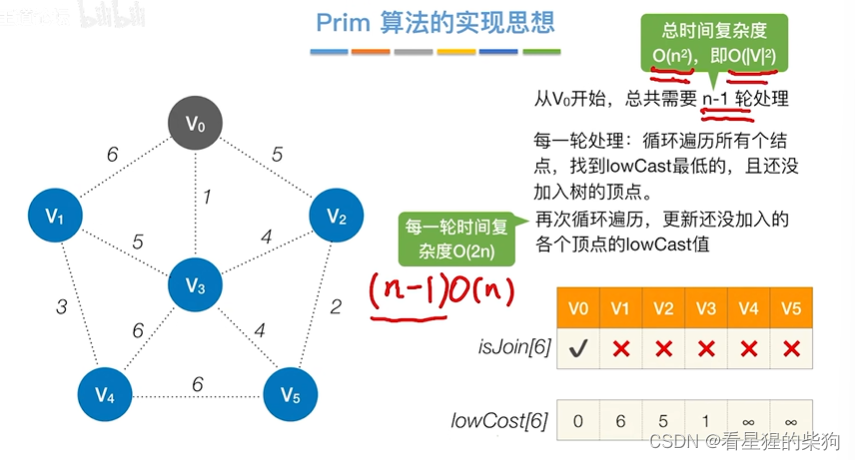
在这里插入图片描述

Kruskal的实现

查找并查集（如果用二叉树实现的）的根需要log2E
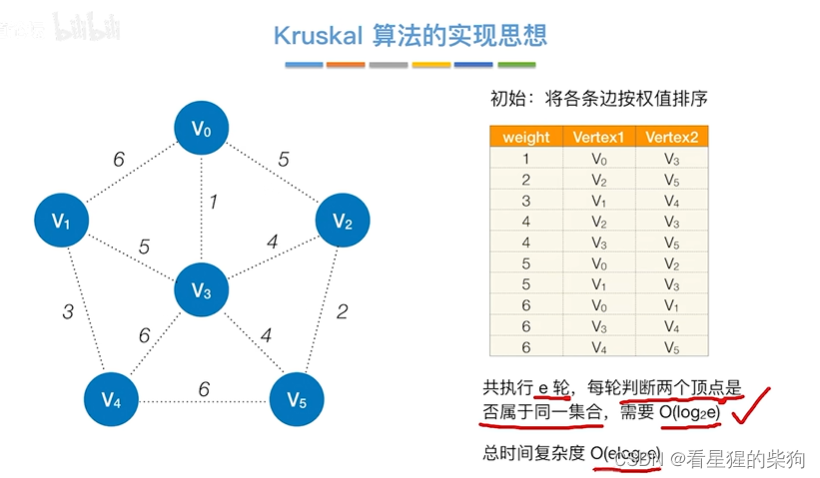
在这里插入图片描述

小结

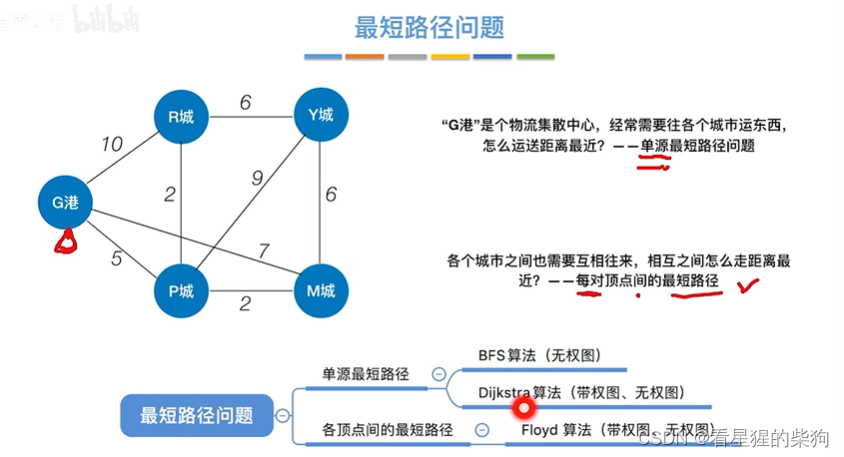
在这里插入图片描述

最短路径问题

在这里插入图片描述

单源最短路径问题

BFS求无权图的单源最短路径

首先访问2号顶点，然后再更新其相邻顶点后的结果
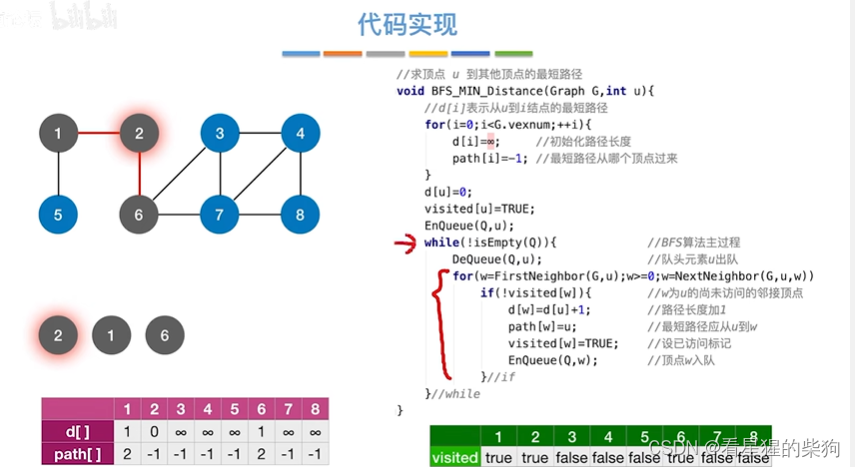
在这里插入图片描述
然后1号顶点出队，相邻节点入队，同时更新各相邻节点
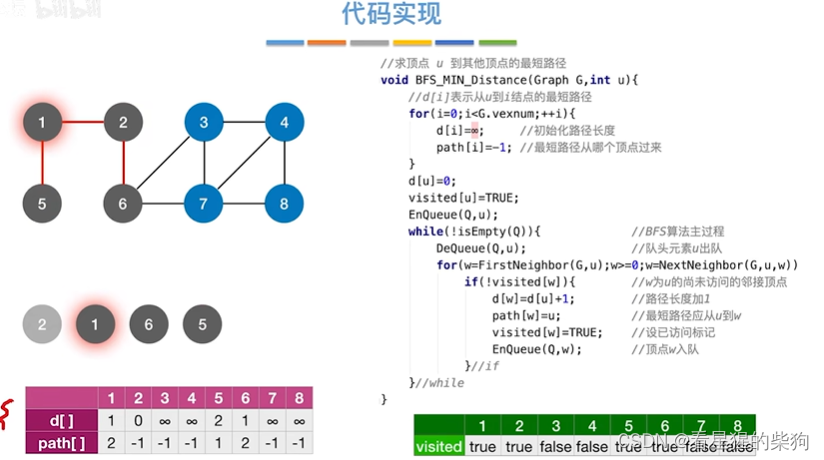
在这里插入图片描述
然后6号顶点出队，更新相邻节点，同时各个相邻节点入队
在这里插入图片描述
5号顶点没有相邻
所以到3号顶点处理
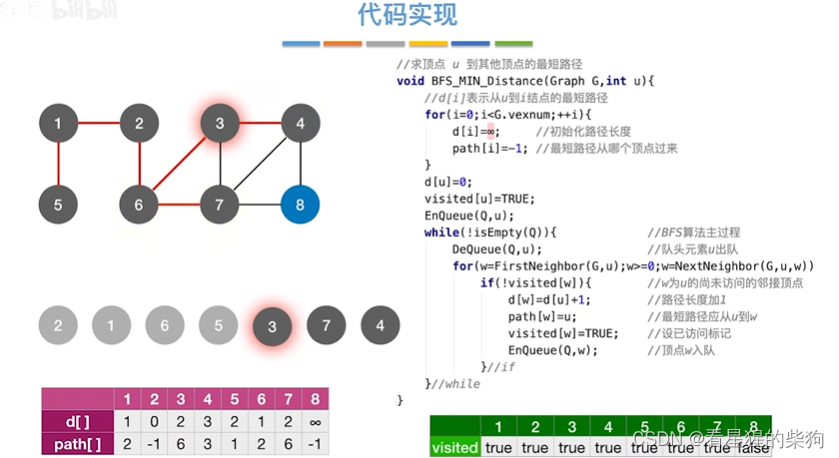
在这里插入图片描述
7号顶点处理
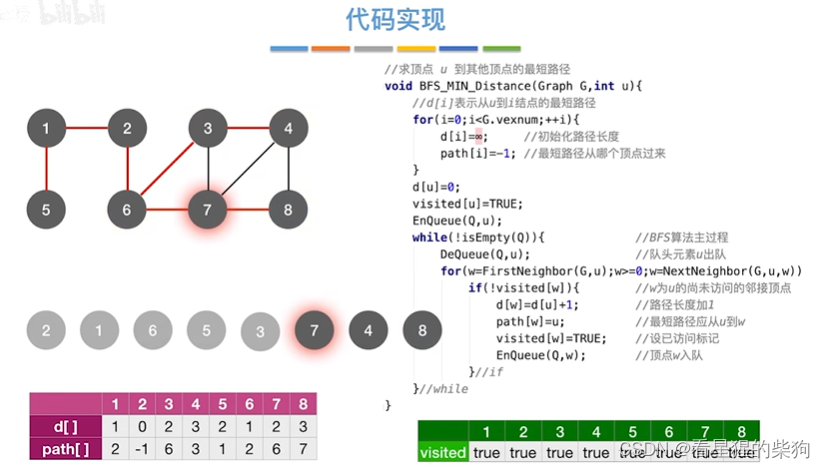
在这里插入图片描述
4号和8号相邻节点都被访问，所以没有处理

小结

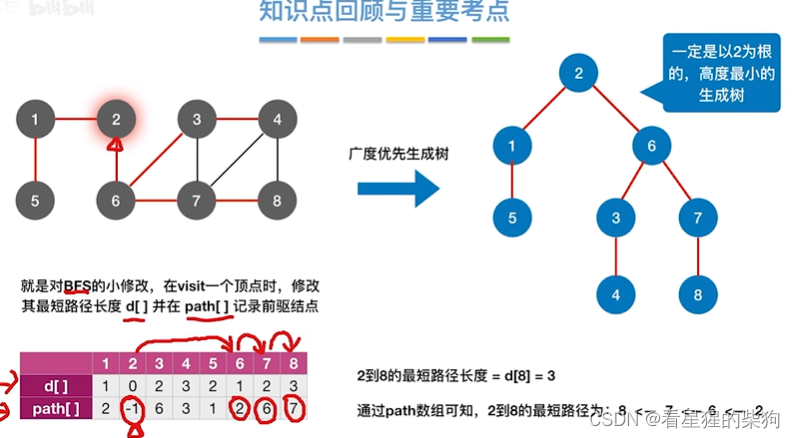
在这里插入图片描述

Dijkastra算法

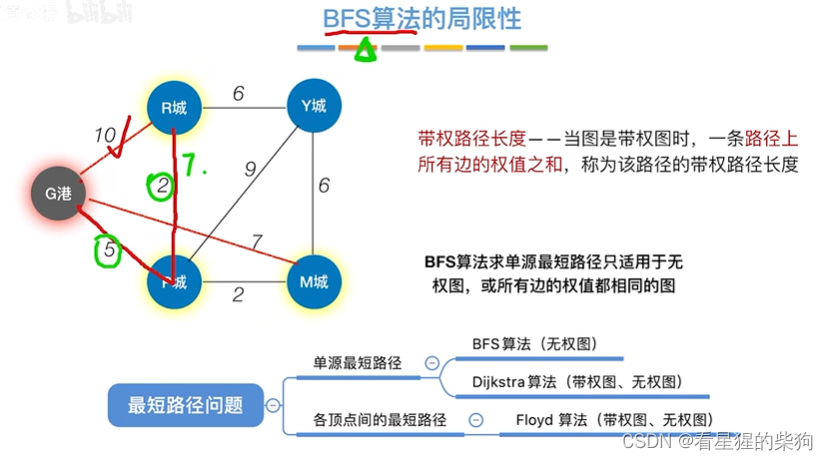
BFS局限性（默认每条路径长度一样）
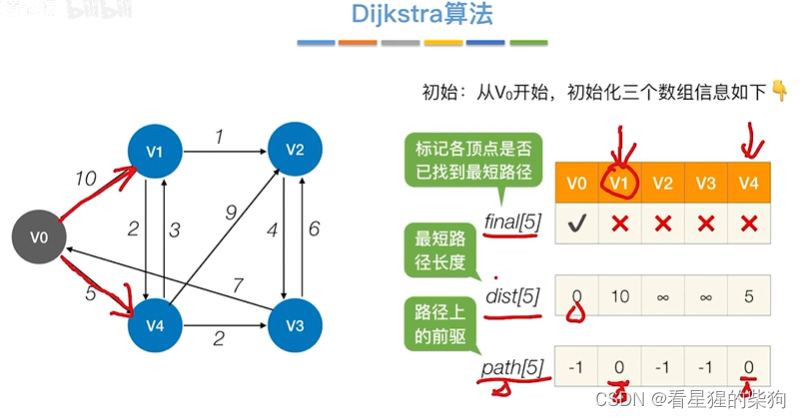
在这里插入图片描述
初始化后，即更新初始节点及其相邻节点
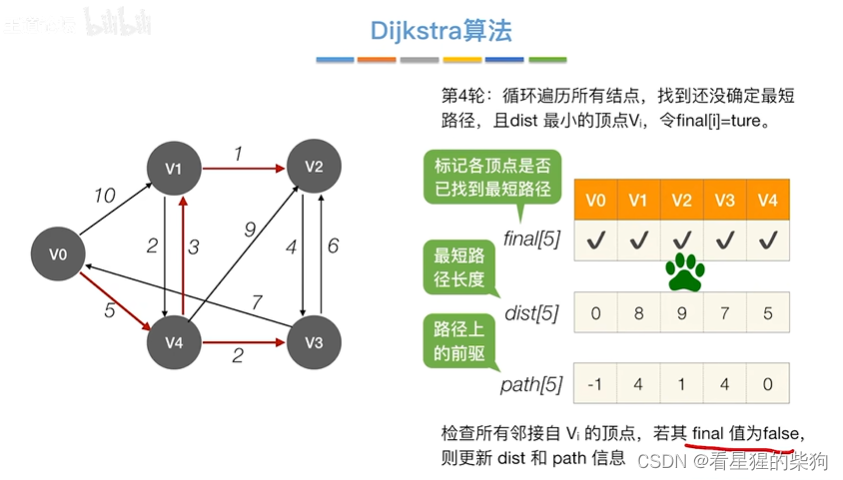
在这里插入图片描述
第一轮后
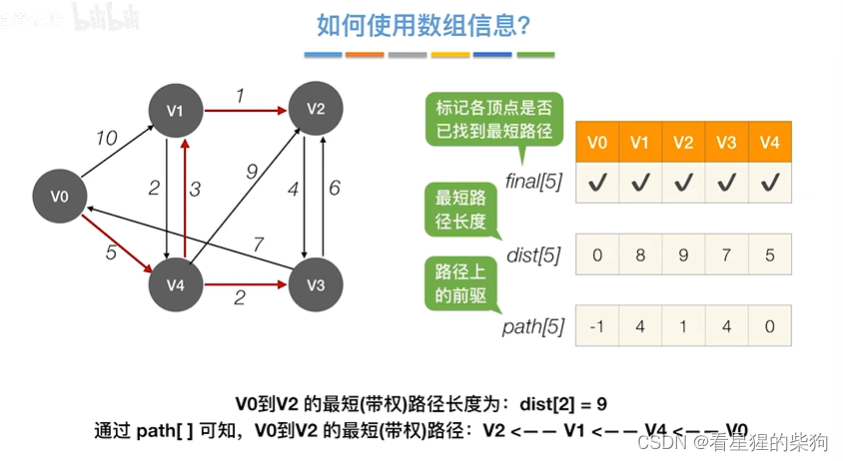
在这里插入图片描述
第二轮后
在这里插入图片描述

第三轮后
在这里插入图片描述
第四轮后

在这里插入图片描述
查找两个顶点的最短路径
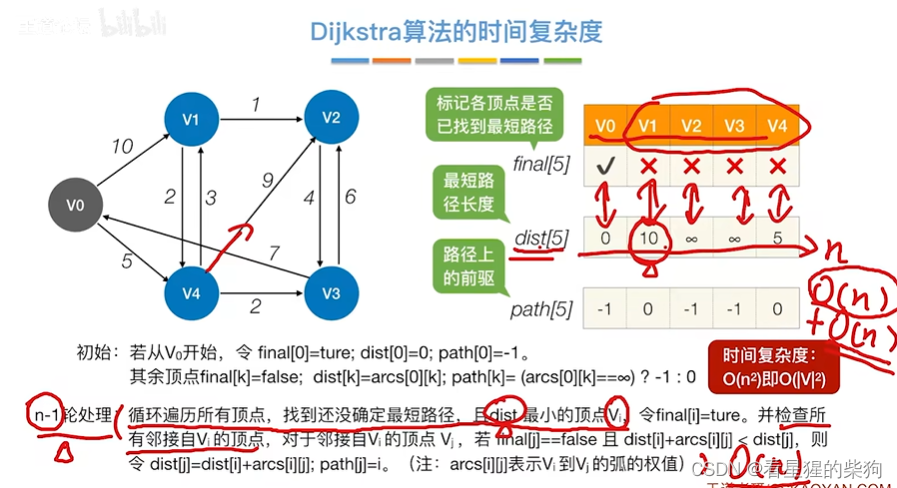
在这里插入图片描述

算法时间复杂度

在这里插入图片描述

在这里插入图片描述

不适用情况

在这里插入图片描述

每一对顶点的最短路径问题

在这里插入图片描述

Floyd算法

初始时
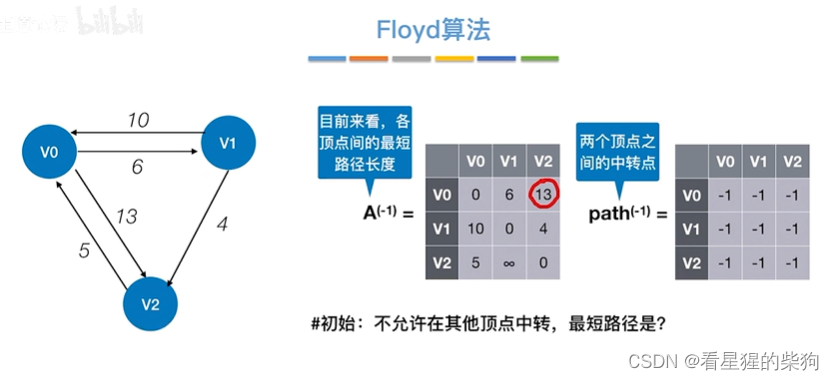
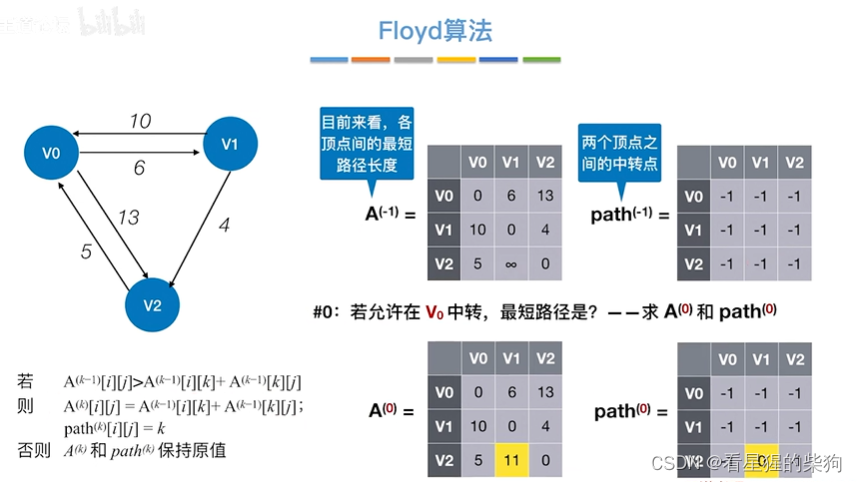
在这里插入图片描述
允许在v0中转
在这里插入图片描述
允许在v0 v1中转
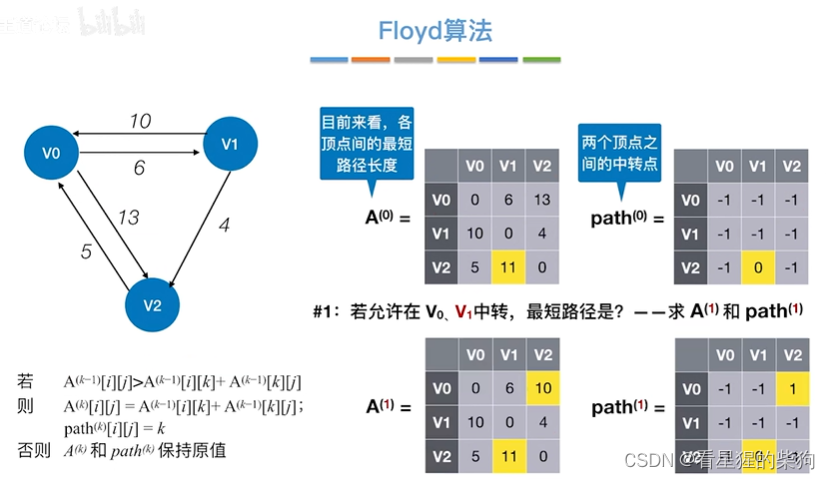
在这里插入图片描述
允许在v0 v1 v2中转
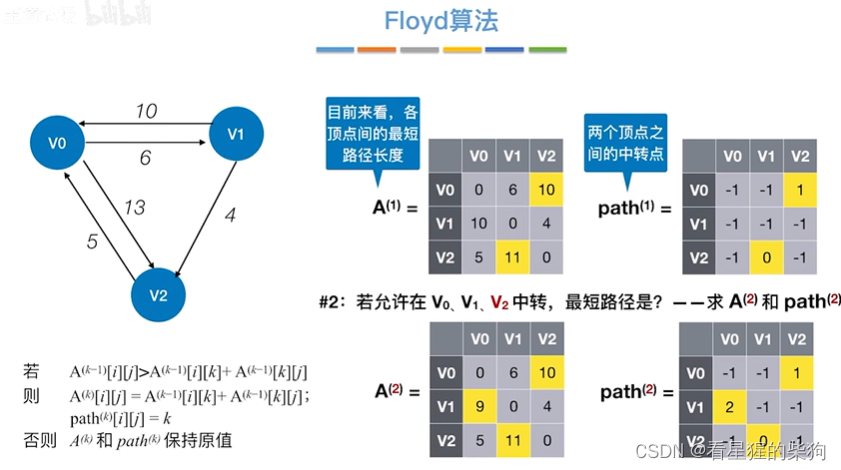
在这里插入图片描述

找两个点的最短路径

在这里插入图片描述

核心代码

空间复杂度是有n*n个矩阵那么多
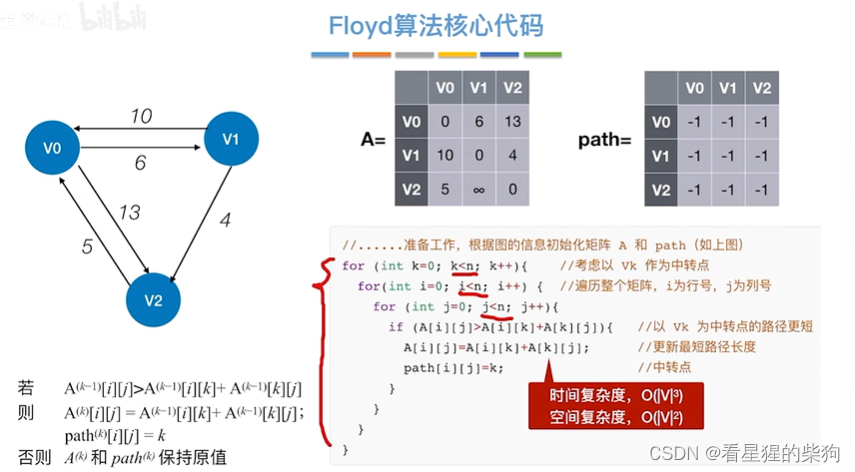
在这里插入图片描述

实例

初始
在这里插入图片描述
允许在v0中转
发现没有变化
从图可以发现v0没有进去的边，所以自然没法中转
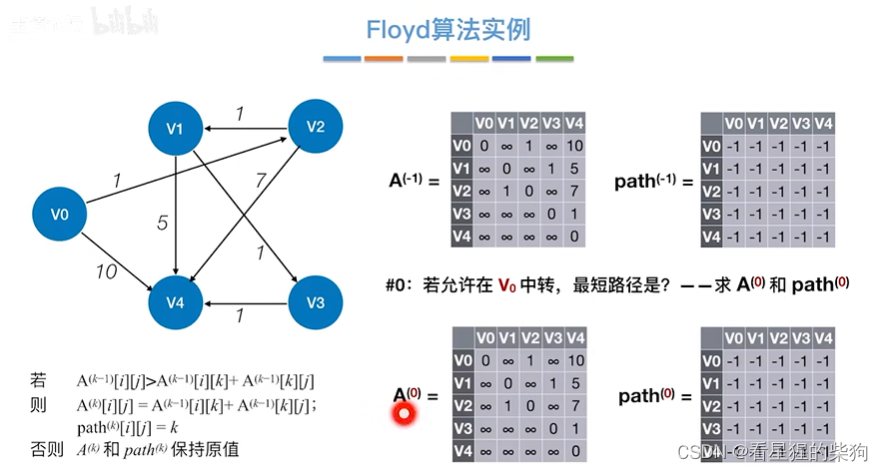
在这里插入图片描述
允许在v0 v1中转
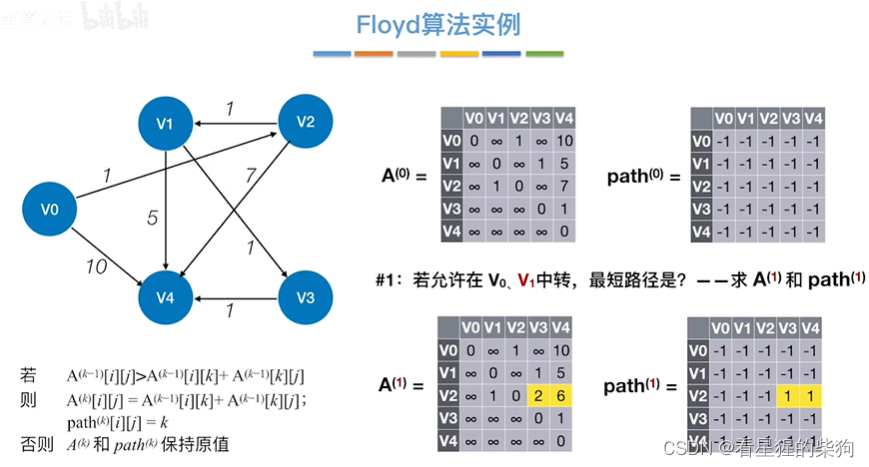
在这里插入图片描述
允许在v0 v1 v2中转
是已经基于之前v0 v1的中转结果的
例如v2到v3是基于中转v1的，但是在以v2中转的转换中是把它认为是相连的
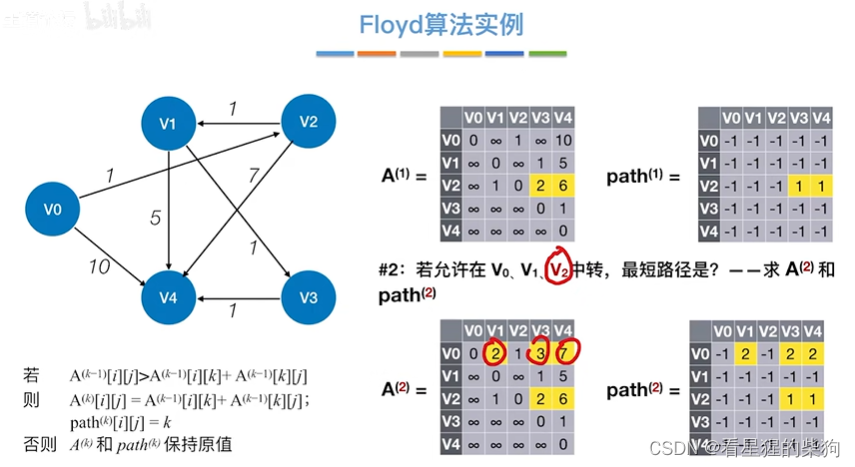
在这里插入图片描述
在这里插入图片描述
允许在v0 v1 v2 v3中转

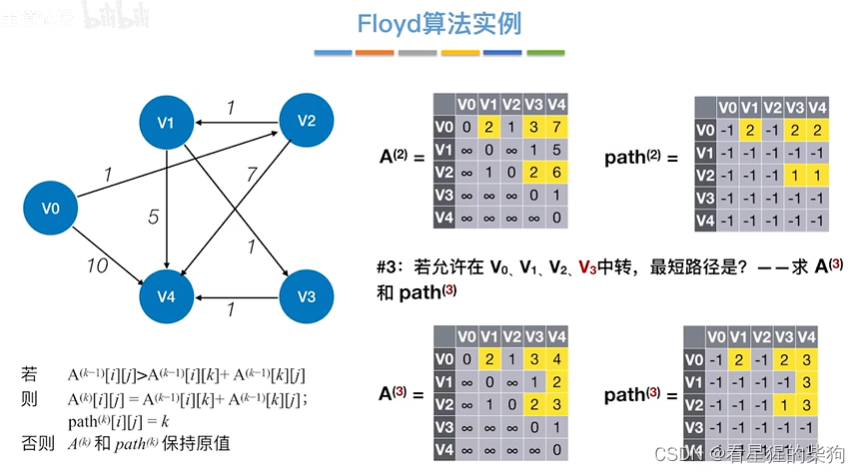
在这里插入图片描述
允许在v0 v1 v2 v3 v4中转
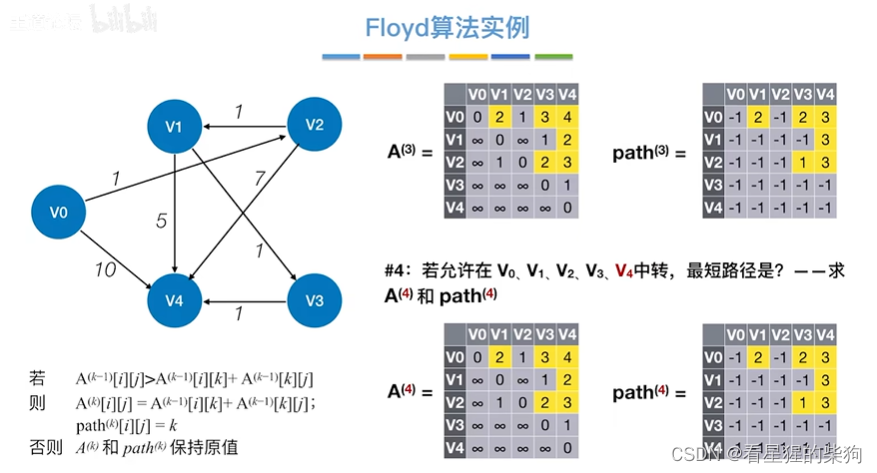
在这里插入图片描述

找两个顶点最短路径

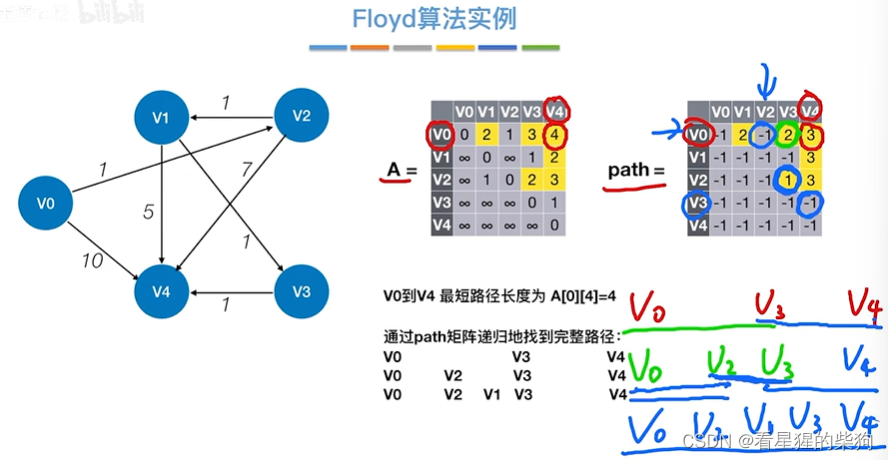
在这里插入图片描述

Floyd用于负权图

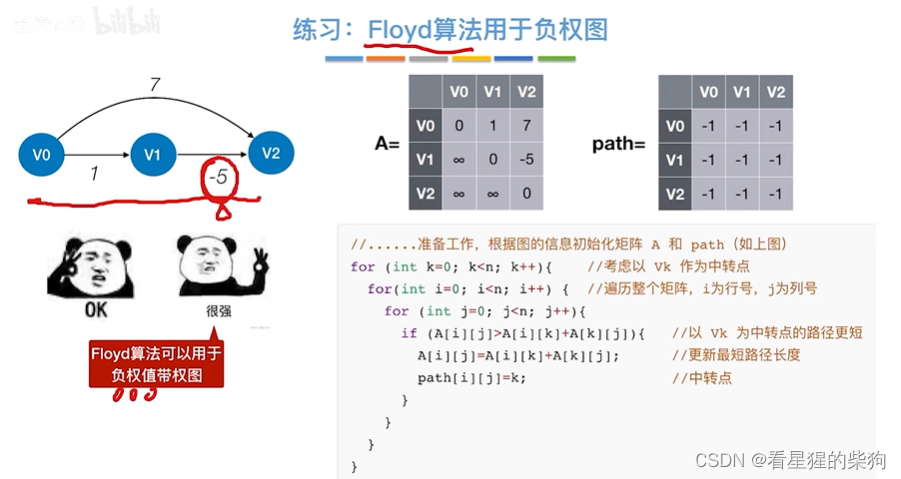
在这里插入图片描述

不能解决的问题

回路越多，路径越短

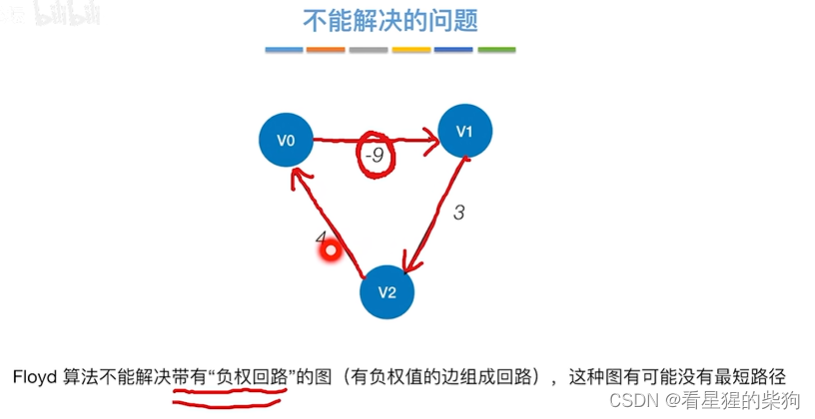
在这里插入图片描述

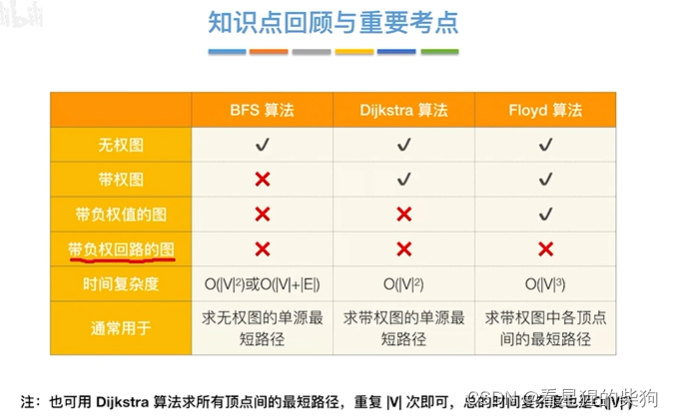
小结

BFS 采用邻接矩阵是V的平方 邻接矩阵是V+E
在这里插入图片描述

相关文章：

数据结构和算法-最小生成树（prim和krusakal）和最短路径问题（BFS和dijkastra和floyd）

文章目录 最小生成树总览生成树广度优先生成树深度优先生成树最小生成树Prim算法Kruskal算法Prim vs KrusakalPrim的实现Kruskal的实现 小结 最短路径问题单源最短路径问题BFS求无权图的单源最短路径小结Dijkastra算法算法时间复杂度不适用情况 每一对顶点的最短路径问题Floyd算…...

编程日记 2023/12/17 15:34:14

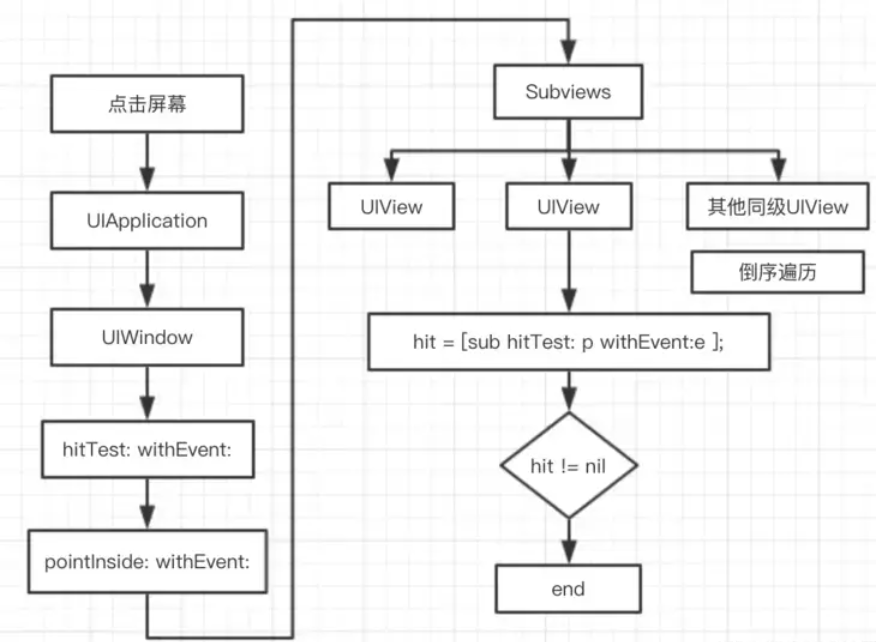
响应者链概述

响应者链 iOS事件的3大类型 Touch Events(触摸事件)Motion Events(运动事件，比如重力感应和摇一摇等)Remote Events(远程事件，比如用耳机上得按键来控制手机) 触摸事件 处理触摸事件的两个步骤 寻找事件的最佳响应者事件的响应在响应链中的传递 寻…...

编程日记 2023/12/17 15:33:12

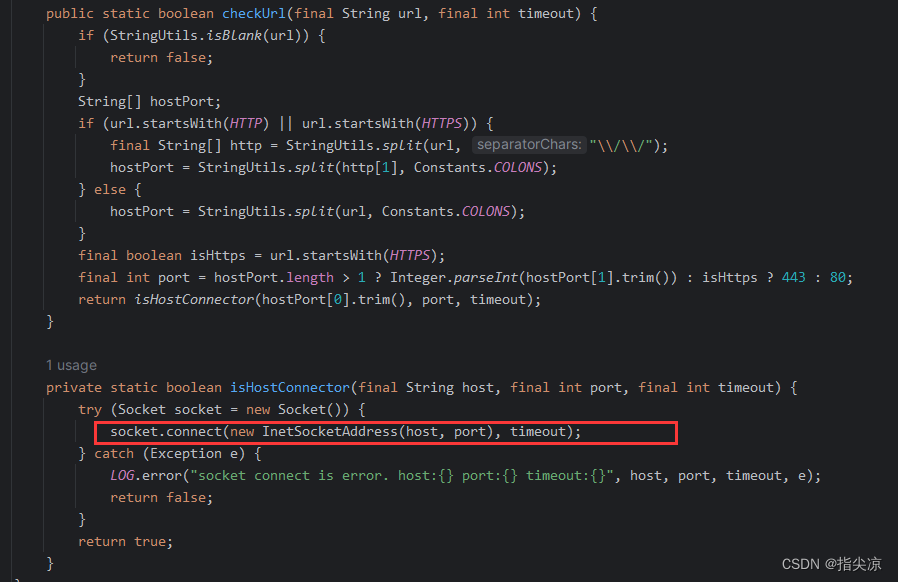
ShenYu网关Http服务探活解析

文章目录 网关端服务探活admin端服务探活 Shenyu HTTP服务探活是一种用于检测HTTP服务是否正常运行的机制。它通过建立Socket连接来判断服务是否可用。当服务不可用时，将服务从可用列表中移除。 网关端服务探活 以divide插件为例，看下divide插件是如何获…...

编程日记 2023/12/17 15:31:11

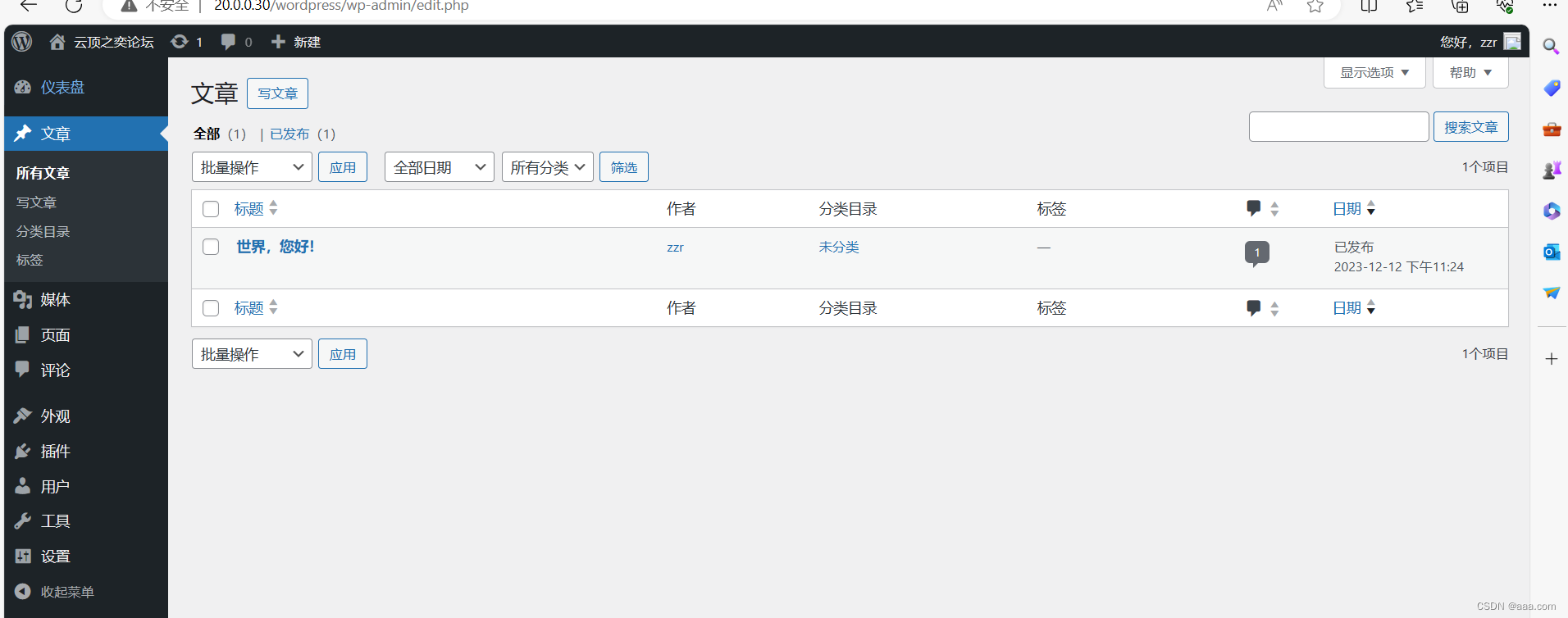
基于dockerfile搭建LNMP

组件自定义IP所需组件nginx172.111.0.10nginxwordpressmysql172.111.0.20mysql-5.7.20php172.111.0.30php LNMP介绍 L：Linux平台，操作系统，另外桑组件的运行平台 N：nginx 提供前端页面 M：MySQL，开源关系的…...

编程日记 2023/12/17 15:30:10

基于VGG-16+Android+Python的智能车辆驾驶行为分析—深度学习算法应用(含全部工程源码)+数据集+模型（三）

目录 前言总体设计系统整体结构图系统流程图 运行环境模块实现1. 数据预处理2. 模型构建3. 模型训练及保存1）模型训练2）模型保存 4. 模型生成1）模型导入及调用2）相关代码（1）布局文件（2&#xff…...

编程日记 2023/12/17 15:29:09

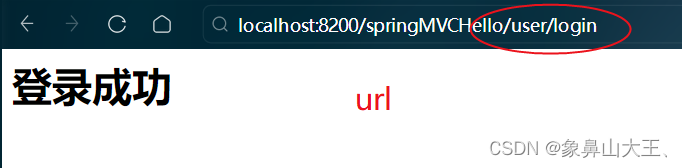
springMVC-@RequestMapping

基本介绍 RequestMapping注解可以指定控制器/处理器的某个方法的请求的url, 示例 （结合springMVC基本原理理解） Controller public class UserHandler {RequestMapping(value "/login")public String login() {System.out.println("登…...

编程日记 2023/12/17 15:28:08

智能优化算法应用：基于树种算法3D无线传感器网络(WSN)覆盖优化 - 附代码

智能优化算法应用：基于树种算法3D无线传感器网络(WSN)覆盖优化 - 附代码 文章目录 智能优化算法应用：基于树种算法3D无线传感器网络(WSN)覆盖优化 - 附代码1.无线传感网络节点模型2.覆盖数学模型及分析3.树种算法4.实验参数设定5.算法结果6.参考文献7.MA…...

编程日记 2023/12/17 15:27:07

web前端项目-影视网站开发

影视网站 本项目主要使用到了 HTML&#xff1b;CSS&#xff1b;JavaScript脚本技术&#xff1b;AJAX无刷新技术&#xff1b;jQuery等技术实现了动态影视网页 运行效果&#xff1a; 一&#xff1a;index.html <!DOCTYPE> <html lang"en"> <head>…...

编程日记 2023/12/17 15:26:06

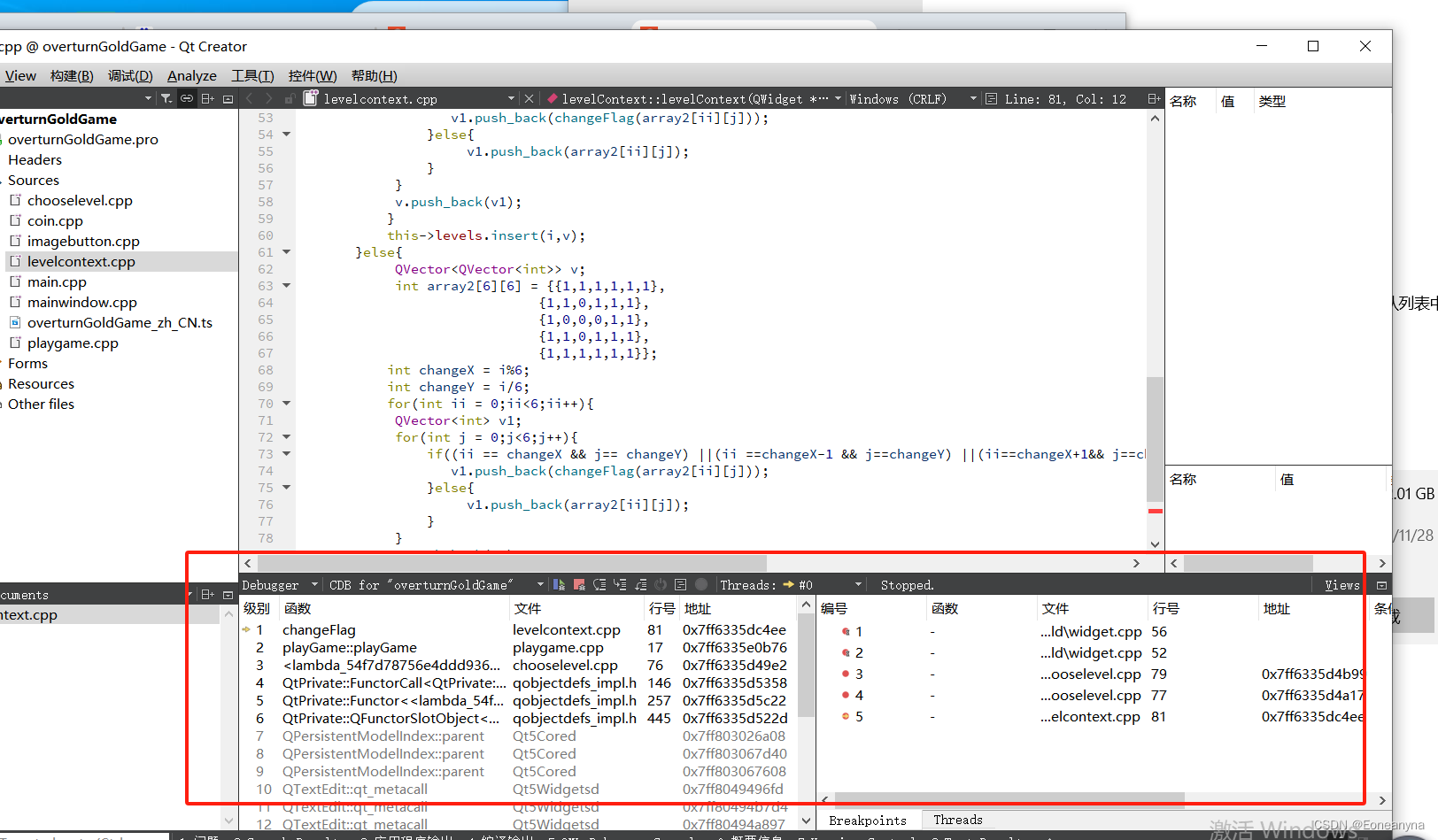
QT:Unable to create a debugging engine.

debug跑不了&#xff1a; 报错&#xff1a;Unable to create a debugging engine. 参考&#xff1a; https://blog.csdn.net/u010906468/article/details/104716198 先检查是否安装了DEBUG插件 工具-》》选项 查看插件&#xff0c;如果没有的话&#xff0c;需要重新安装qt时…...

编程日记 2023/12/17 15:24:04

如何理解Rust语言中的“impl”关键字

在Rust编程语言中&#xff0c;impl是一个关键字&#xff0c;用于为类型实现方法和特性&#xff08;traits&#xff09;。impl关键字后面可以跟一个类型或者特性名称&#xff0c;然后在大括号中定义该类型或特性的具体实现。 当我们使用impl关键字为一个类型实现方法时&#xf…...

编程日记 2023/12/17 15:23:03

C++实现简单的猜数字小游戏

猜数字 小游戏介绍&#xff1a;猜数字游戏是令游戏机随机产生一个100以内的正整数&#xff0c;用户输入一个数对其进行猜测&#xff0c;需要你编写程序自动对其与随机产生的被猜数进行比较&#xff0c;并提示大了&#xff0c;还是小了&#xff0c;相等表示猜到了。如果猜到&…...

编程日记 2023/12/17 15:22:02

人工智能导论复习资料

题型 1、简答题&#xff08;5题&#xff09; 2、设计题 3、综合题 4、论述题&#xff08;10分&#xff09; 考点 第一章 1、人工智能的定义、发展&#xff1b; 2、人工智能的学派、认知观及其间的关系&#xff1b; 3、人工智能要素及系统分类&#xff1b; 4、人工智能的研究、…...

编程日记 2023/12/17 15:21:01

Sentinel使用详解

组件简介 Sentinel是阿里开源的一套用于服务容错的综合性解决方案。它以流量为切入点&#xff0c;从流量控制、熔断降级、系统负载保护等多个维度来保护服务的稳定性。Sentinel承接了阿里巴巴近10年的双十一大促流量的核心场景&#xff0c;例如秒杀、消息削峰填谷、集群流量控…...

编程日记 2023/12/17 15:17:59

Vue3源码梳理：响应式系统的前世今生

响应性数据的前世 js的程序性: 一套固定的&#xff0c;不会发生变化的执行流程 1 &#xff09;没有响应的数据 // 定义商品对象 const product {price: 10,quantity: 2 }// 总价格 let total product.price * product.quantity console.log(总价格&#xff1a;${total}) //…...

编程日记 2023/12/17 15:16:58

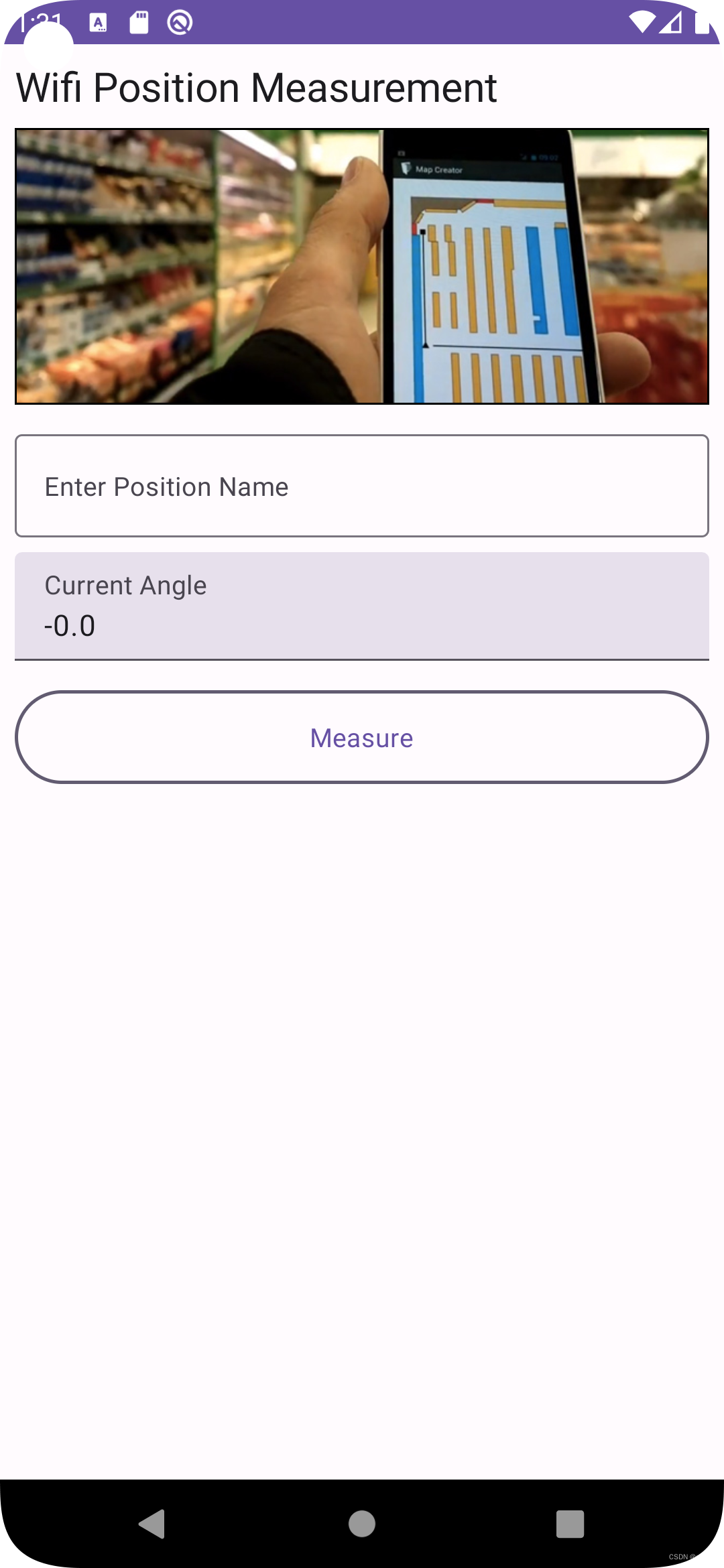
Jetpack Compose开发一个Android WiFi导航应用

在以前的一篇文章构建一个WIFI室内定位系统_wifi定位系统-CSDN博客中&#xff0c;我介绍了如何用Android来测量WiFi信号&#xff0c;上传到服务器进行分析后&#xff0c;生成室内不同地方的WiFi指纹&#xff0c;从而帮助进行室内导航。当时我是用的HTML5的技术来快速开发一个An…...

编程日记 2023/12/17 15:15:58

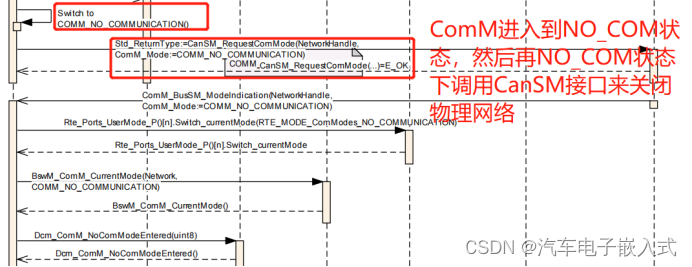
【Mode Management】ComM详细介绍

目录 1. Introduction and functional overview 2.Dependencies to other modules 3.Functional specification 3.1 Partial Network Cluster Management 3.2 ComM channel state machine 3.2.1 Behaviour in state COMM_NO_COMMUNICATION 3.2.1.1 COMM_NO_COM_NO_PENDI…...

编程日记 2023/12/17 15:11:54

【C++多线程编程】（二）之详解锁（lock）和解锁（unlock）

在C多线程编程中&#xff0c;锁&#xff08;lock&#xff09;和解锁&#xff08;unlock&#xff09;通常用于管理共享资源的访问&#xff0c;以防止多个线程同时对资源进行修改&#xff0c;从而避免竞态条件&#xff08;Race Condition&#xff09;和数据不一致性问题。C标准库…...

编程日记 2023/12/17 15:10:53

【Mypy】超级实用的python高级库！

今天&#xff0c;我很兴奋地向大家介绍一个神奇的Python库&#xff1a;Mypy。这个库是Python世界中的一颗璀璨明星&#xff0c;提供了静态类型检查的强大功能&#xff0c;极大地增强了Python这门动态类型语言的健壮性和可维护性。我们将深入探索Mypy的多个方面&#xff0c;并通…...

编程日记 2023/12/17 15:09:51

【Python基础】循环语句

文章目录 [toc]什么是循环Python中的循环方式while循环格式示例 什么是循环 程序中需要重复执行的代码&#xff0c;可以通过循环实现比如和女朋友道歉&#xff0c;或一万遍“宝宝&#xff0c;我错了”&#xff0c;在没有学习循环之前&#xff0c;我们只能通过如下方式实现 pr…...

编程日记 2023/12/17 15:01:45

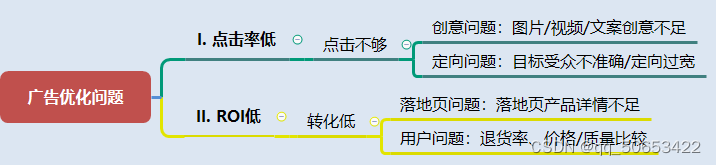
【面试】广告优化

a1&#xff1a;点击率公式是什么&#xff1f;点击率低的原因是什么&#xff1f; 点击率点击/曝光&#xff0c;点击率低的原因主要有两点&#xff1a;一是创意不吸引人&#xff1b;二是目标受众不准确/定向过宽不精确&#xff0c;广告曝光给了对产品不感兴趣用户 a2&#xff1a;…...

编程日记 2023/12/17 15:00:44

HTML 语义化

目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案&#xff1a; 语义化标签&#xff1a; <header>&#xff1a;页头<nav>&#xff1a;导航<main>&#xff1a;主要内容<article>&#x…...

编程新知 2025/10/4 16:37:34

云启出海，智联未来｜阿里云网络「企业出海」系列客户沙龙上海站圆满落地

借阿里云中企出海大会的东风&#xff0c;以**「云启出海&#xff0c;智联未来&#xff5c;打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办&#xff0c;现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

编程新知 2025/10/11 14:43:49

前端导出带有合并单元格的列表

// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

编程新知 2025/10/10 10:30:13

今日科技热点速览

&#x1f525; 今日科技热点速览 &#x1f3ae; 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售&#xff0c;主打更强图形性能与沉浸式体验&#xff0c;支持多模态交互&#xff0c;受到全球玩家热捧 。 &#x1f916; 人工智能持续突破 DeepSeek-R1&…...

编程新知 2025/9/25 1:53:11

JavaScript基础-API 和 Web API

在学习JavaScript的过程中&#xff0c;理解API&#xff08;应用程序接口&#xff09;和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能&#xff0c;使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

编程新知 2025/8/21 23:03:46

【从零学习JVM|第三篇】类的生命周期(高频面试题)

前言&#xff1a; 在Java编程中&#xff0c;类的生命周期是指类从被加载到内存中开始&#xff0c;到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期&#xff0c;让读者对此有深刻印象。 目录 ​…...

编程新知 2025/9/28 3:36:18

C++ 设计模式 《小明的奶茶加料风波》

&#x1f468;‍&#x1f393; 模式名称&#xff1a;装饰器模式&#xff08;Decorator Pattern&#xff09; &#x1f466; 小明最近上线了校园奶茶配送功能&#xff0c;业务火爆&#xff0c;大家都在加料&#xff1a; 有的同学要加波霸 &#x1f7e4;&#xff0c;有的要加椰果…...

编程新知 2025/9/28 3:38:54

es6+和css3新增的特性有哪些

一&#xff1a;ECMAScript 新特性&#xff08;ES6&#xff09; ES6 (2015) - 革命性更新 1&#xff0c;记住的方法&#xff0c;从一个方法里面用到了哪些技术 1&#xff0c;let /const块级作用域声明2&#xff0c;**默认参数**&#xff1a;函数参数可以设置默认值。3&#x…...

编程新知 2025/9/30 4:32:03

C++_哈希表

本篇文章是对C学习的哈希表部分的学习分享 相信一定会对你有所帮助~ 那咱们废话不多说&#xff0c;直接开始吧&#xff01; 一、基础概念 1. 哈希核心思想&#xff1a; 哈希函数的作用&#xff1a;通过此函数建立一个Key与存储位置之间的映射关系。理想目标&#xff1a;实现…...

编程新知 2025/9/29 12:06:03

​​企业大模型服务合规指南：深度解析备案与登记制度​​

伴随AI技术的爆炸式发展&#xff0c;尤其是大模型&#xff08;LLM&#xff09;在各行各业的深度应用和整合&#xff0c;企业利用AI技术提升效率、创新服务的步伐不断加快。无论是像DeepSeek这样的前沿技术提供者&#xff0c;还是积极拥抱AI转型的传统企业&#xff0c;在面向公众…...

编程新知 2025/10/14 2:53:32