论文笔记:A review on multi-label learning
一、介绍
传统的监督学习是单标签学习,但是现实中一个实例可能对应多个标签。这篇文章介绍了多标签分类的定义和评价指标、多标签学习的算法还有其他相关的任务。
二、问题相关定义
2.1 多标签学习任务
假设 X = R d X = R^d X=Rd,表示d维的输入空间, Y = ( y 1 , y 2 , y 3 . , . . . , y q Y = (y_1, y_2, y_3., ..., y_q Y=(y1,y2,y3.,...,yq表示输出的可能q个类别。多标签任务是学习一个方程,在训练集合 D = { ( x i , Y i ) ∣ 1 ≤ i ≤ m } D = \{(x_i, Y_i)|1 \leq i \leq m\} D={(xi,Yi)∣1≤i≤m}学习一个X到Y的函数。对于每个多标签实例, x i ∈ X x_i \in X xi∈X是d维特征空间 ( x i 1 , x i 2 , . . . , x i d ) T (x_{i1}, x_{i2}, ..., x_{id})^T (xi1,xi2,...,xid)T, Y i ⊆ Y Y_i \subseteq Y Yi⊆Y是对应于 x x x的标签几何。多标签学习任务就是学习一个多标签分类器 h ( . ) h(.) h(.),对于没有见到过的实例 x ∈ X x \in X x∈X,可以预测他的标签 h ( x ) ⊆ Y h(x) \subseteq Y h(x)⊆Y。
2.2 多标签学习的特点
2.2.1. 不同数据集多标签的程度可能不同
有几个有用的多标签指示符可以用于描述多标签数据集的特性。
- 最自然的方法就是衡量多标签程度的是label cardinality(标签基数):
L C a r d ( D ) = 1 m ∑ i = 1 m ∣ Y i ∣ LCard(D) = \frac{1}{m}\sum_{i=1}^m|Y_i| LCard(D)=m1i=1∑m∣Yi∣
表示每个样本的平均标签数目。 - “标签密度”(label density)按标签空间中可能的标签数规范化标签基数:
L D e n ( D ) = 1 y ⋅ L C a r d ( D ) LDen(D) = \frac{1}{y} \cdot LCard(D) LDen(D)=y1⋅LCard(D) - 标签多样性:Label diversity
L D i v ( D ) = ∣ Y ∣ e x i s t s x : ( x , Y ) ∈ D ∣ LDiv(D) = |{Y|exists x:(x,Y)\in D}| LDiv(D)=∣Y∣existsx:(x,Y)∈D∣
数据集中出现的不同标签集的数目 - 标签多样性可以通过数据集的数量来标准化,以表示不同标签集的比例
P L D i v ( D ) = 1 D ⋅ L D i v ( D ) PLDiv(D)=\frac{1}{D}\cdot LDiv(D) PLDiv(D)=D1⋅LDiv(D)
多标签学习就是学习x和y的相关性,希望 f ( x , y ′ ) ≥ f ( x , y ′ ′ ) f(x, y^{'}) \ge f(x, y^{''}) f(x,y′)≥f(x,y′′),其中 y ′ ∈ Y y' \in Y y′∈Y, y ′ ′ ∉ Y y^{''}\notin Y y′′∈/Y。所以多标签分类器可以通过函数f(.,.)得到: h ( x ) = { y ∣ f ( x , y ) ≥ t ( x ) , y ∈ Y } h(x) = \{y | f(x,y) \ge t(x), y\in Y\} h(x)={y∣f(x,y)≥t(x),y∈Y},其中 t ( x ) t(x) t(x),扮演阈值函数的角色,把标签空间对分成相关的标签集和不相关的标签集。阈值函数可以由训练集产生,可以设为常数。
2.2.2. 标签具有相互关系
学习策略
多标签学习的主要难点在于输出空间的爆炸增长,有效的挖掘标签之间的相关性,是多标签学习成功的关键。根据对相关性挖掘的强弱,可以把多标签算法分为三类。
- 一阶学习策略:忽略和其它标签的相关性,比如把多标签分解成多个独立的二分类问题(简单高效)。
- 二阶学习策略:考虑标签之间的成对关联,比如为相关标签和不相关标签排序。
- 高阶学习策略:考虑多个标签之间的关联,比如对每个标签考虑所有其它标签的影响(效果最优)。
2.2.3 数据不平衡
一. 某个类别对应样例可能远多于另一个类别,类别之间不平衡
二. 某个类别对应的正样本可能远多于负样本(类别之内不平衡)
2.3 阈值校准
多标签学习中的一种常见做法是返回一些实值函数 f ( ⋅ , ⋅ ) f(·,·) f(⋅,⋅)作为学习模型。为了决定最后的输出结果,每个标签上的实值输出应根据阈值函数输出 t ( x ) t(x) t(x)进行校准。
通常有两种方法设置 t ( ∗ ) t(*) t(∗),设置 t ( ∗ ) t(*) t(∗)为常量或者从训练数据中预测。对于前者, f f f是一个实值函数,所以t可设置为0。当 f f f的输出为概率时, t t t设置为0.5。或者当测试集可见时,阈值可以设置为训练集合测试集的多标签程度指标区别最小的数。
对于后一个策略,可以用stacking-style的步骤来决定阈值函数。假设 t t t是一个线性模型,即 t ( x ) = < w , f ( x ) > + b t(x) = <w, f(x)> + b t(x)=<w,f(x)>+b,这里 f ( x ) = ( f ( x , y 1 ) , . . . , f ( x , y q ) ) T ∈ R q f(x) = (f(x, y1),...,f(x,y_q))^T \in R^q f(x)=(f(x,y1),...,f(x,yq))T∈Rq是一个 q q q维stacking向量。为了学习 w ∗ w^* w∗和 b ∗ b^* b∗,需要求解线性最小二乘。
m i n w ∗ , b ∗ ∑ i − 1 m ( < w ∗ , f ∗ ( x i ) > + b ∗ − s ( x i ) ) 2 min_{w^*,b^*}\sum_{i-1}^m(<w^*,f^*(x_i)> + b^* - s(x_i))^2 minw∗,b∗i−1∑m(<w∗,f∗(xi)>+b∗−s(xi))2
s ( x i ) = a r g m i n a ∈ R ( ∣ { y j ∣ y j ∈ Y i , f ( x i , y j ) ≤ a } ∣ + ∣ { y k ∣ y k ∈ Y ^ i , f ( x i , y k ) ≥ a } ∣ ) s(x_i)=argmin_{a\in R}(|\{y_j | y_j \in Y_i, f(x_i, y_j) \leq a\}|+|\{y_k|y_k \in \hat Y_i, f(x_i, y_k) \geq a\}|) s(xi)=argmina∈R(∣{yj∣yj∈Yi,f(xi,yj)≤a}∣+∣{yk∣yk∈Y^i,f(xi,yk)≥a}∣)表示模型的输出目标,对每个样本,它以最小误差将 Y Y Y划分为相关和不相关。
2.4 评价指标
2.4.1 分类评价指标
- Examples-based metrics 基于样本评价指标
通过分别评估学习系统在每个测试示例上的性能,然后返回整个测试集的平均值 - Label-based metrics 基于标签评价指标
通过分别评估每个类标签上的学习系统性能,然后返回所有类标签上的宏/微观平均值
2.4.2 排序评价指标

下面对每个指标进行介绍
基于样本的评价指标
- Subset Accuracy(衡量正确率,预测的样本集和真实的样本集完全一样就是正确)
s u b s e t a c c ( h ) = 1 p ∑ i = 1 p [ h ( x i ) = Y i ] subsetacc(h) = \frac{1}{p} \sum_{i=1}^p[h(x_i) = Y_i] subsetacc(h)=p1i=1∑p[h(xi)=Yi] - Hamming Loss(衡量的是错分的标签比例,正确标签没有被预测以及错误标签被预测的标签占比)
h l o s s ( h ) = 1 p ∑ i = 1 p ∣ h ( x i ) Δ Y i ∣ hloss(h) = \frac{1}{p}\sum_{i=1}^p|h(x_i)\Delta Y_i| hloss(h)=p1i=1∑p∣h(xi)ΔYi∣
Δ \Delta Δ表示两个集合的对称差,返回只在其中一个集合出现的那些值。 - Accuracy, Precision, Recall, F值(单标签学习中准确率,精准率,召回率,F值)
A c c u r a c y ( h ) = 1 p ∑ i = 1 p ∣ h ( x i ) ∩ y i ∣ ∣ h ( x i ) ∪ y i ∣ Accuracy(h)=\frac{1}{p}∑_{i=1}^p\frac{∣h(x_i)∩y_i∣}{|h(x_i)∪y_i|} Accuracy(h)=p1i=1∑p∣h(xi)∪yi∣∣h(xi)∩yi∣
P r e c i s i o n ( h ) = 1 p ∑ i = 1 p Y i ∩ h ( x i ) h ( x i ) Precision(h) = \frac{1}{p}\sum_{i=1}^p\frac{Y_i \cap h(x_i)}{h(x_i)} Precision(h)=p1i=1∑ph(xi)Yi∩h(xi)
R e c a l l = 1 p ∑ i = 1 p Y i ∩ h ( x i ) Y i Recall = \frac{1}{p}\sum_{i=1}^p\frac{Y_i \cap h(x_i)}{Y_i} Recall=p1i=1∑pYiYi∩h(xi)
F = 1 + β 2 ⋅ P r e c i s i o n ( h ) ⋅ R e c a l l ( h ) β 2 ⋅ ( P r e c i s i o n ( h ) + R e c a l l ( h ) ) F = \frac{1 + \beta^2 \cdot Precision(h) \cdot Recall(h)}{\beta^2 \cdot (Precision(h) + Recall(h))} F=β2⋅(Precision(h)+Recall(h))1+β2⋅Precision(h)⋅Recall(h) - one-error(“预测到的最相关的标签” 不在 “真实标签”中的样本占比。值越小,表现越好)
o n e − e r r o r ( f ) = 1 p ∑ i = 1 p [ a r g m a x y ∈ Y f ( x i , y ) ∉ Y i ] one-error(f) = \frac{1}{p}\sum_{i=1}^p[argmax_{y \in Y}f(x_i, y)\notin Y_i] one−error(f)=p1i=1∑p[argmaxy∈Yf(xi,y)∈/Yi] - Coverage(值越小,表现越好)
c o v e r a g e ( f ) = 1 p ∑ i p m a x y ∈ Y i r a n k f ( x i , y ) − 1 coverage(f) = \frac{1}{p}\sum_{i}^p max_{y \in Y_i } rank_{f_(x_i,y)}-1 coverage(f)=p1i∑pmaxy∈Yirankf(xi,y)−1 - Ranking loss(值越小,表现越好)
r l o s s ( f ) = 1 p ∑ i = 1 p 1 ∣ Y i ∣ ∣ Y ^ i ∣ ∣ { ( y ′ , y ′ ′ ) ∣ f ( x i , y ′ ) ≤ f ( x i , y ′ ′ ) , ( y ′ , y ′ ′ ) ∈ Y i × Y ^ i } ∣ rloss(f) = \frac{1}{p}\sum_{i=1}^p \frac{1}{|Y_i| |\hat Y_i|} |\{(y',y^{''})|f(x_i, y') \leq f(x_i, y^{''}),(y', y^{''}) \in Y_i \times \hat Y_i \}| rloss(f)=p1i=1∑p∣Yi∣∣Y^i∣1∣{(y′,y′′)∣f(xi,y′)≤f(xi,y′′),(y′,y′′)∈Yi×Y^i}∣ - Average Precision(度量比特定标签更相关的那些标签的排名的占比,越大越好)
a v g p r e c ( f ) = 1 p ∑ i = 1 p 1 ∣ Y i ∣ ∑ y ∈ Y i ∣ y ′ ∣ r a n k f ( x , y ′ ) ≤ r a n k f ( x i , y ) , y ′ ∈ Y i ∣ r a n k f ( x i , y ) avgprec(f)=\frac{1}{p}\sum_{i=1}^p\frac{1}{|Y_i|}\sum_{y \in Y_i}\frac{|{y'|rank_f(x,y') \leq rank_f(x_i,y),y'\in Y_i }|}{rank_{f(x_i,y)}} avgprec(f)=p1i=1∑p∣Yi∣1y∈Yi∑rankf(xi,y)∣y′∣rankf(x,y′)≤rankf(xi,y),y′∈Yi∣
基于标签的评价指标 - 分类评价指标
对于每个标签,都可以得到 T P , F P , T N , F N TP, FP, TN, FN TP,FP,TN,FN

用 B ( T P j , F P j , T N j , F N j ) B(TP_j, FP_j, TN_j, FN_j) B(TPj,FPj,TNj,FNj)表示特定的二元分类度量 B ∈ { A c c u r a c y , P r e c i s i o n , R e c a l l , F β } B \in \{Accuracy, Precision, Recall, F^{\beta}\} B∈{Accuracy,Precision,Recall,Fβ},label-based的分类可以通过两种方式得到
- Macro-averaging(宏平均,先对单个标签下的数量特征计算得到常规指标,再对多个标签取平均)
B m a c r o ( h ) = 1 q ∑ j = 1 q B ( T P j , F P j , T N j , F N j ) B_{macro(h)} = \frac{1}{q}\sum_{j=1}^qB(TP_j,FP_j,TN_j,FN_j) Bmacro(h)=q1j=1∑qB(TPj,FPj,TNj,FNj) - Micro-averaging(微平均,对数据集中的每一个实例不分类别进行统计建立全局混淆矩阵,然后计算相应指标)
B m i c r o ( h ) = B ( ∑ j = 1 q T P j , ∑ j = 1 q F P j , ∑ j = 1 q T N j , ∑ j = 1 q F N j ) B_{micro(h)} = B(\sum_{j=1}^q TP_j, \sum_{j=1}^q FP_j, \sum_{j=1}^q TN_j, \sum_{j=1}^q FN_j) Bmicro(h)=B(j=1∑qTPj,j=1∑qFPj,j=1∑qTNj,j=1∑qFNj)
- 排序评价指标 rank metric
-
AUC-macro(“排序正确”的数据对的占比,先对单个标签计算,再平均)
A U C m a c r o = 1 q ∑ j = 1 q A U C j = 1 q ∑ i = 1 q ∣ { ( x ′ , x ′ ′ ) ∣ f ( x ′ , y j ) ≥ f ( x ′ , y j ) , ( x ′ , x ′ ′ ) ∈ Z j × Z ^ j } ∣ ∣ Z j ∣ ∣ Z ^ j ∣ AUC_{macro} = \frac{1}{q}\sum_{j=1}^q AUC_j = \frac{1}{q}\sum_{i=1}^q\frac{|\{(x', x'')|f(x',y_j) \geq f(x',y_j), (x', x'') \in Z_j \times \hat Z_j\}|}{|Z_j||\hat Z_j|} AUCmacro=q1j=1∑qAUCj=q1i=1∑q∣Zj∣∣Z^j∣∣{(x′,x′′)∣f(x′,yj)≥f(x′,yj),(x′,x′′)∈Zj×Z^j}∣
Z j = { x i ∣ y j ∈ Y i , 1 ≤ i ≤ p } Z_j = \{x_i|y_j \in Y_i, 1\leq i \leq p\} Zj={xi∣yj∈Yi,1≤i≤p}表示的是含有 y j y_j yj标签的样本数量,
Z ^ j = { x i ∣ y j ∉ Y i , 1 ≤ i ≤ p } \hat Z_j = \{x_i|y_j \notin Y_i, 1\leq i \leq p\} Z^j={xi∣yj∈/Yi,1≤i≤p}表示的是不含有 y j y_j yj标签的样本数量 -
AUC-micro(“排序正确”的数据对的占比,把多个标签考虑在内来计算占比)
A U C m i c r o = 1 q ∑ j = 1 q A U C j = 1 q ∑ i = 1 q ∣ { ( x ′ , x ′ ′ , y ′ , y ′ ′ ) ∣ f ( x ′ , y ′ ) ≥ f ( x ′ ′ , y ′ ′ ) , ( x ′ , y ′ ) ∈ S + , ( x ′ ′ , y ′ ′ ) ∈ S − } ∣ ∣ S + ∣ ∣ S − ∣ AUC_{micro} = \frac{1}{q}\sum_{j=1}^q AUC_j = \frac{1}{q}\sum_{i=1}^q\frac{|\{(x', x'', y', y'')|f(x',y') \geq f(x'',y''),(x',y')\in S^+,(x'', y'') \in S^-\}|}{|S^+||S^-|} AUCmicro=q1j=1∑qAUCj=q1i=1∑q∣S+∣∣S−∣∣{(x′,x′′,y′,y′′)∣f(x′,y′)≥f(x′′,y′′),(x′,y′)∈S+,(x′′,y′′)∈S−}∣
S + = ( x i , y ) ∣ y ∈ Y i , 1 ≤ i ≤ p S^+ = {(x_i, y)|y\in Y_i, 1 \leq i \leq p} S+=(xi,y)∣y∈Yi,1≤i≤p表示的是相关的样本标签对,
S − = ( x i , y ) ∣ y ∉ Y i , 1 ≤ i ≤ p S^- = {(x_i, y)|y\notin Y_i, 1 \leq i \leq p} S−=(xi,y)∣y∈/Yi,1≤i≤p表示的是不相关的样本标签对
三、多分类学习算法
两种学习方法:
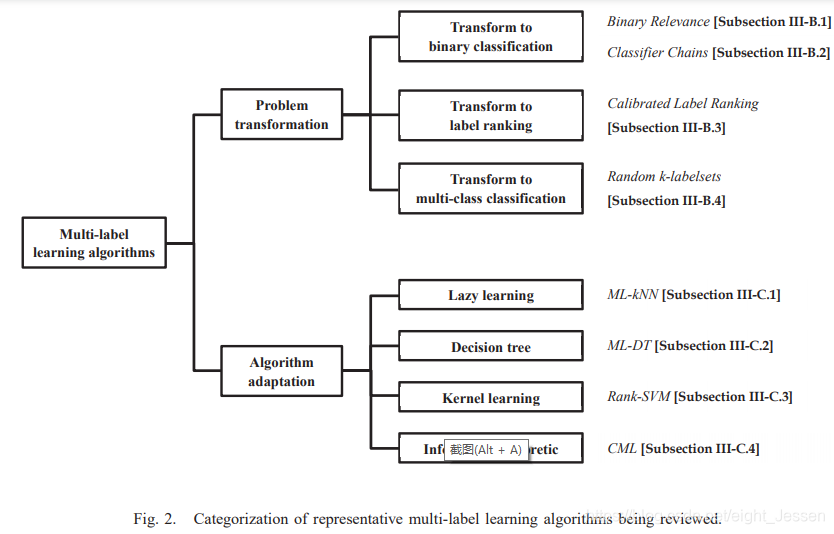
- 问题转换法(让数据适应算法)
把多标签分类转为其他成熟的场景。代表算法有一阶binary revevance和高阶方法classifier chains。他们将多标签问题转为二分类。二阶方法有calibrated label ranking。将多标签分类转为标签排序,高阶方法radom k-labelset将多标签学习转为多分类问题。 - 算法改编方法(让算法适应数据)
更改学习技术来应对多标签数据。代表算法包括一阶方法ML-knn改编k近邻,一阶方法ML-DT改编决策树,二阶方法Rank-SVM改编核技巧,二阶方法CML改编information-theretic techniques。
相关文章:

论文笔记:A review on multi-label learning
一、介绍 传统的监督学习是单标签学习,但是现实中一个实例可能对应多个标签。这篇文章介绍了多标签分类的定义和评价指标、多标签学习的算法还有其他相关的任务。 二、问题相关定义 2.1 多标签学习任务 假设 X R d X R^d XRd,表示d维的输入空间&am…...
接口文档 YAPI介绍
YAPI介绍 YAPI使用流程...

LeetCode 300最长递增子序列 674最长连续递增序列 718最长重复子数组 | 代码随想录25期训练营day52
动态规划算法10 LeetCode 300 最长递增子序列 2023.12.15 题目链接代码随想录讲解[链接] int lengthOfLIS(vector<int>& nums) {//创建变量result存储最终答案,设默认值为1int result 1;//1确定dp数组,dp[i]表示以nums[i]为结尾的子数组的最长长度ve…...

Improving IP Geolocation with Target-Centric IP Graph (Student Abstract)
ABSTRACT 准确的IP地理定位对于位置感知的应用程序是必不可少的。虽然基于以路由器为中心(router-centric )的IP图的最新进展被认为是前沿的,但一个挑战仍然存在:稀疏IP图的流行(14.24%,少于10个节点,9.73%孤立)限制了图的学习。为了缓解这个问题,我们将目标主机(ta…...

华为技面三轮面试题
1. 最长回文子串 -- 中心扩散法 给你一个字符串 s,找到 s 中最长的回文子串。 如果字符串的反序与原始字符串相同,则该字符串称为回文字符串。 示例 1: 输入:s "babad" 输出:"bab" 解释&…...
Linux arm架构下构建Electron安装包
上篇文章我们介绍 Electron 基本的运行开发与 windows 安装包构建简单流程,这篇文章我们从零到一构建 Linux arm 架构下安装包,实际上 Linux arm 的构建流程,同样适用于 Linux x86 环境,只不过需要各自的环境依赖,Linu…...
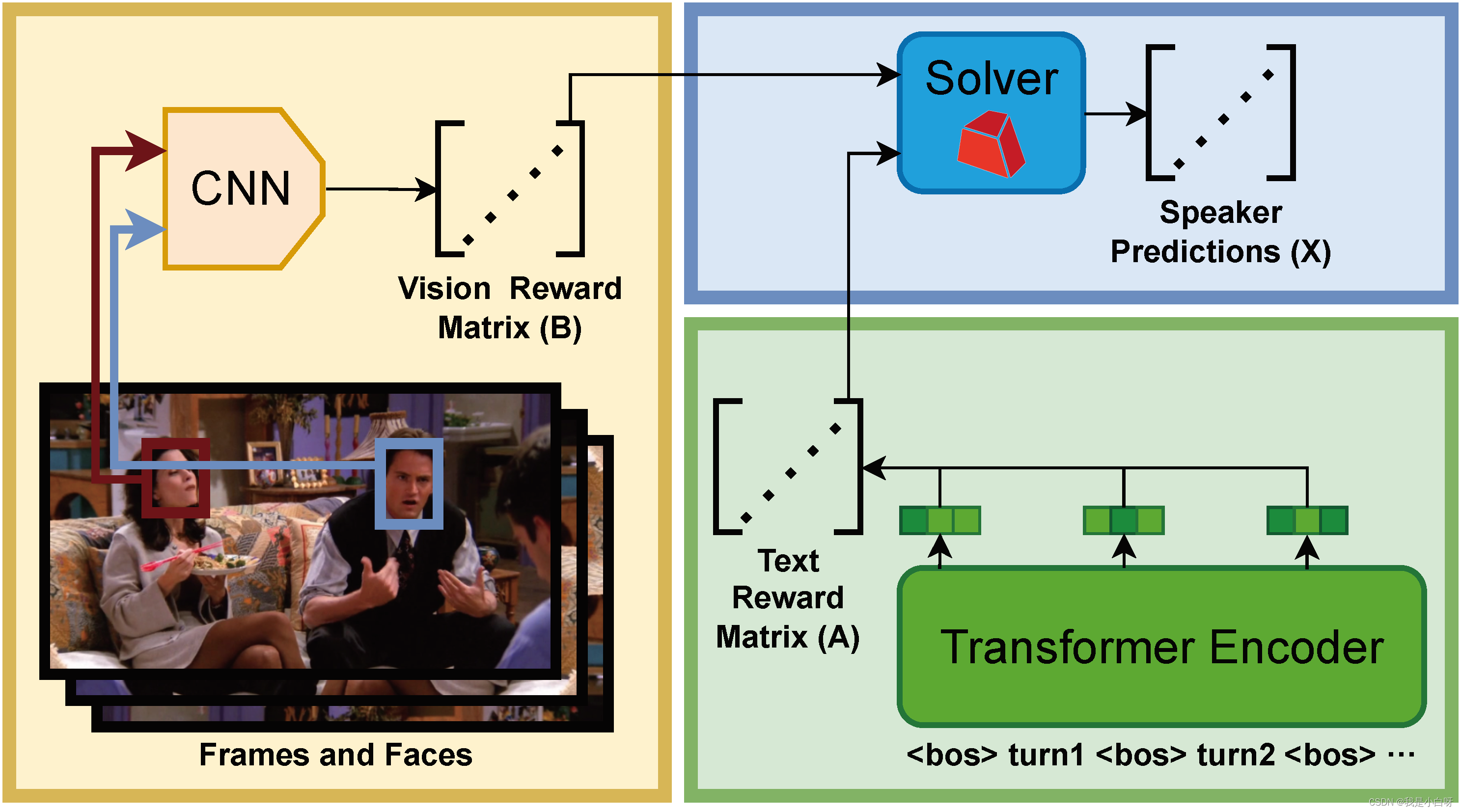
【CCF BDCI 2023】多模态多方对话场景下的发言人识别 Baseline 0.71 NLP 部分
【CCF BDCI 2023】多模态多方对话场景下的发言人识别 Baseline 0.71 NLP 部分 概述NLP 简介文本处理词嵌入上下文理解 文本数据加载to_device 函数构造数据加载样本数量 len获取样本 getitem 分词构造函数调用函数轮次嵌入 RobertaRoberta 创新点NSP (Next Sentence Prediction…...

推免那些事
平生第一次搞推免,也是最后一次。错失了一些机会,也有幸获得了一些机会,值得祝庆,也值得反思。 以下记录为个人流水账。 个人背景 我的背景可以算不是非常好了,况且今年211受歧视比较严重。 学校:211&…...

华清远见嵌入式学习——QT——作业2
作业要求: 代码运行效果图: 登录失败 和 最小化 和 取消登录 登录成功 和 X号退出 代码: ①:头文件 #ifndef LOGIN_H #define LOGIN_H#include <QMainWindow> #include <QLineEdit> //行编辑器类 #include…...
C# Winfrm 编写一个天气查看助手
#前言# 最近这个北方的天气啊经常下雪,让我想起来我上学时候写的那个天气预报小功能了,今天又复现了一下,哈哈哈,大家当个乐子看哈! 1.创建项目 2.添加引用 上图所示,下载所需天气预报标识,网站…...

基于SpringBoot和微信小程序的农场信息管理系统
文章目录 项目介绍主要功能截图:部分代码展示设计总结项目获取方式🍅 作者主页:超级无敌暴龙战士塔塔开 🍅 简介:Java领域优质创作者🏆、 简历模板、学习资料、面试题库【关注我,都给你】 🍅文末获取源码联系🍅 项目介绍 基于SpringBoot和微信小程序的农场信息管…...

Linux统计网卡流量
cat /proc/net/dev Linux 内核提供了一种通过 /proc 文件系统,在运行时访问内核内部数据结构、改变内核设置的机制。proc文件系统是一个伪文件系统,它只存在内存当中,而不占用外存空间。它以文件系统的方式为访问系统内核数据的操作提供接口。…...
设计可编辑表格组件
前言 什么是可编辑表格呢?简单来说就是在一个表格里面进行表单操作,执行增删改查。这在一些后台管理系统中是尤为常见的。 今天我们根据vue2 element-ui来设计一个表单表格组件。(不涉及完整代码,想要使用完整功能可以看底部连…...

低代码是美食!!!
一、什么是低代码 低代码是一种软件开发方法,通过图形化界面和少量手写代码,让开发者能够更迅速、简单地构建应用程序。相比传统的编码方式,低代码平台提供了可视化的开发工具和预构建的组件,使开发过程更加快捷高效。 二、低代码…...
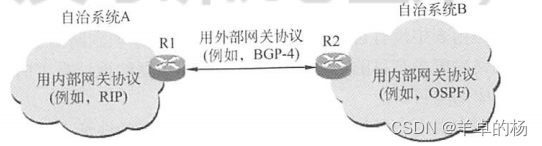
计算机网络网络层(期末、考研)
计算机网络总复习链接🔗 目录 路由算法静态路由与动态路由距离-向量算法链路状态路由算法层次路由 IPv4(这个必考)IPv4分组IPv4地址与NAT子网划分与子网掩码、CIDRARP、DHCP与ICMP地址解析协议ARP动态主机配置协议DHCP IPv6IPv6特点 路由协议…...

LCR 120. 寻找文件副本
解题思路: 利用增强for循环遍历documents,将遇见的id加入hmap中,如果id在hamp中存在,则直接返回id class Solution {public int findRepeatDocument(int[] documents) {Set<Integer> hmapnew HashSet<>();for(int d…...

git切换分支
切换到你想要保留的分支: 确保你在本地已经切换到了你想要保留的分支。 git checkout 要保留的分支名更改远程仓库地址: 如果你还没有更改远程仓库地址,使用 git remote set-url 来更改它。 git remote set-url origin 新的仓库地址推送当前分…...

Android 在UploadEventService使用ThreadPoolManager线程管理传递数据给后台
Android 在UploadEventService使用ThreadPoolManager线程管理传递数据给后台,如何实现呢? 可以通过以下步骤使用ThreadPoolManager线程管理传递数据给后台: 创建一个ThreadPoolManager类来管理线程池,比如: public cl…...
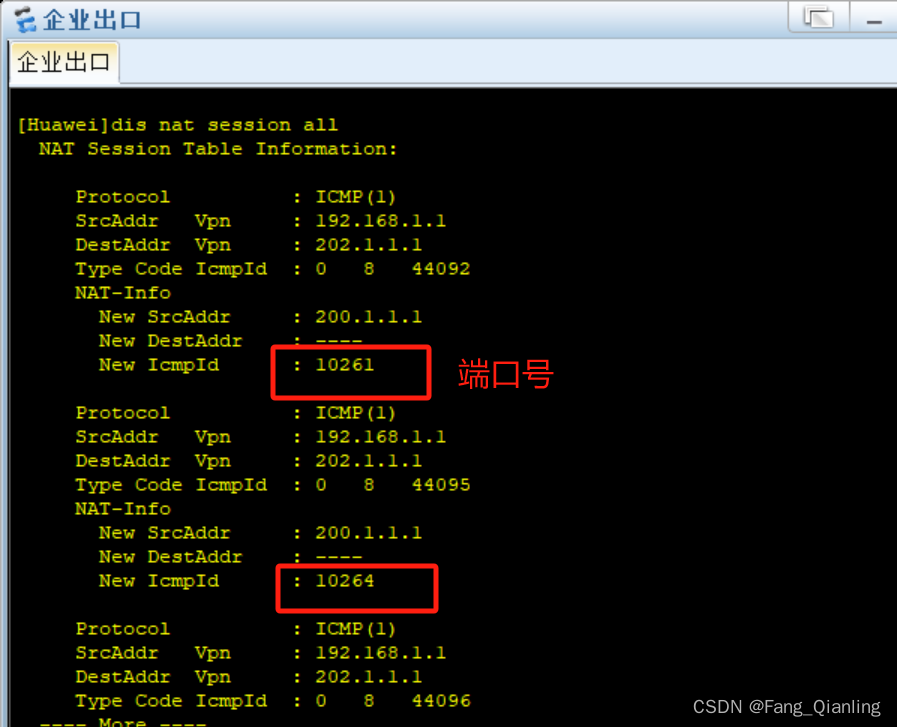
网络(十)ACL和NAT
前言 网络管理在生产环境和生活中,如何实现拒绝不希望的访问连接,同时又要允许正常的访问连接?当下公网地址消耗殆尽,且公网IP地址费用昂贵,企业访问Internet全部使用公网IP地址不够现实,如何让私网地址也…...
)
JavaScript算法46- 最长连续序列(leetCode:128middle)
128. 最长连续序列 一、题目 给定一个未排序的整数数组 nums ,找出数字连续的最长序列(不要求序列元素在原数组中连续)的长度。 请你设计并实现时间复杂度为 O(n) 的算法解决此问题。 示例 输入:nums [100,4,200,1,3,2] 输出…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

如何通过git命令查看项目连接的仓库地址?
要通过 Git 命令查看项目连接的仓库地址,您可以使用以下几种方法: 1. 查看所有远程仓库地址 使用 git remote -v 命令,它会显示项目中配置的所有远程仓库及其对应的 URL: git remote -v输出示例: origin https://…...
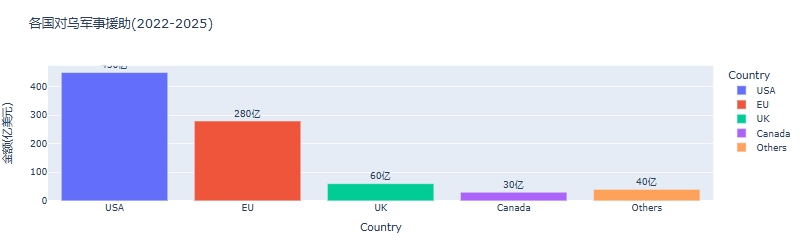
python可视化:俄乌战争时间线关键节点与深层原因
俄乌战争时间线可视化分析:关键节点与深层原因 俄乌战争是21世纪欧洲最具影响力的地缘政治冲突之一,自2022年2月爆发以来已持续超过3年。 本文将通过Python可视化工具,系统分析这场战争的时间线、关键节点及其背后的深层原因,全面…...
