当前位置：首页 > news >正文

【数据结构】八大排序之希尔排序算法

news 文章来源：https://blog.csdn.net/weixin_72357342/article/details/135043566 2025/1/12 15:45:39

🦄个人主页:修修修也

🎏所属专栏:数据结构

⚙️操作环境:Visual Studio 2022

一.优化直接插入排序算法

我们在之前对直接插入排序算法的优化部分通过对直接插入排序的分析可以得到一个结论,即:

进行直接插入排序的数组,如果越接近局部有序,则后续进行直接插入排序算法时其时间复杂度就会越低.

所谓基本有序,就是指小的关键字基本在前面,大的关键字基本在后面,而不大不小的基本在中间.

例如下面这个数组序列,虽然它还是无序的状态,甚至是局部逆序的状态,但至少它的前8个数据"0-7"都在前半部分,后8个数据"8-15"都在后半部分,这样就比完全逆序状态更接近基本有序,相应的算法执行的次数也直接减少了一半:

当我们再进一步,将它们整合的更加接近局部有序一些,可以发现,这时算法的总执行次数又直接减少了一半:

而当我们整合到最接近局部有序时,可以发现,这时算法的总执行次数表达式中的n^2项就已经消失了:

我们已经知道了如果将数组整合成局部有序,就可以大大优化直接插入排序,问题是如何通过预排序将数列整合成局部有序呢?

其实很简单,我们将这些数字不断分为gap组,然后分别让相隔gap个元素的一组数据保持有序就可以了:

如下,第一次我们将数组分为8组,然后使相隔8个元素的每组数据都保持有序,即第一组数据"15和7"要调整为顺序,则将其二者调换位置即可,后续七组操作同理:

然后我们就可以得到如下数组了:

接着,我们再将数组分为4组,让每隔4个元素的数据保持有序,即第一组数据"7,3,15,11"要调整为顺序,则将其看作一个代排数组,然后用直接插入排序将其调整为"3,7,11,15"的顺序,后面7组同理:

然后我们就可以得到如下数组:

我们继续再将数组分为2组,让每隔2个元素的数据保持有序,即将第一组数据"3,1,7,5,11,9,15,13"直接插入排序,将其调整为"1,3,5,7,9,11,13,15"的顺序,第二组同理:

然后我们就可以得到如下数组:

然后就是最后一步,我们将数组看作一组,让相邻的两个元素的数据保持有序,即将全组数据直接插入排序,就可以得到最终结果:

至此,其实我们对直接插入排序的优化过程,就是希尔排序算法的思路.

二.希尔排序简介及思路

希尔排序(Shell Sort)是一种插入排序算法.

它的基本思想是:

先选定一个整数,把待排序文件中所有数据分成gap个组,所有距离为gap的数据分在同一组内,并对每一组内的数据进行排序.
重复上述分组和排序的工作,当达到gap=1时,所有数据在统一组内排好序.

算法动图演示如下:

三.希尔排序算法的代码实现

算法实现步骤:(以升序为例)

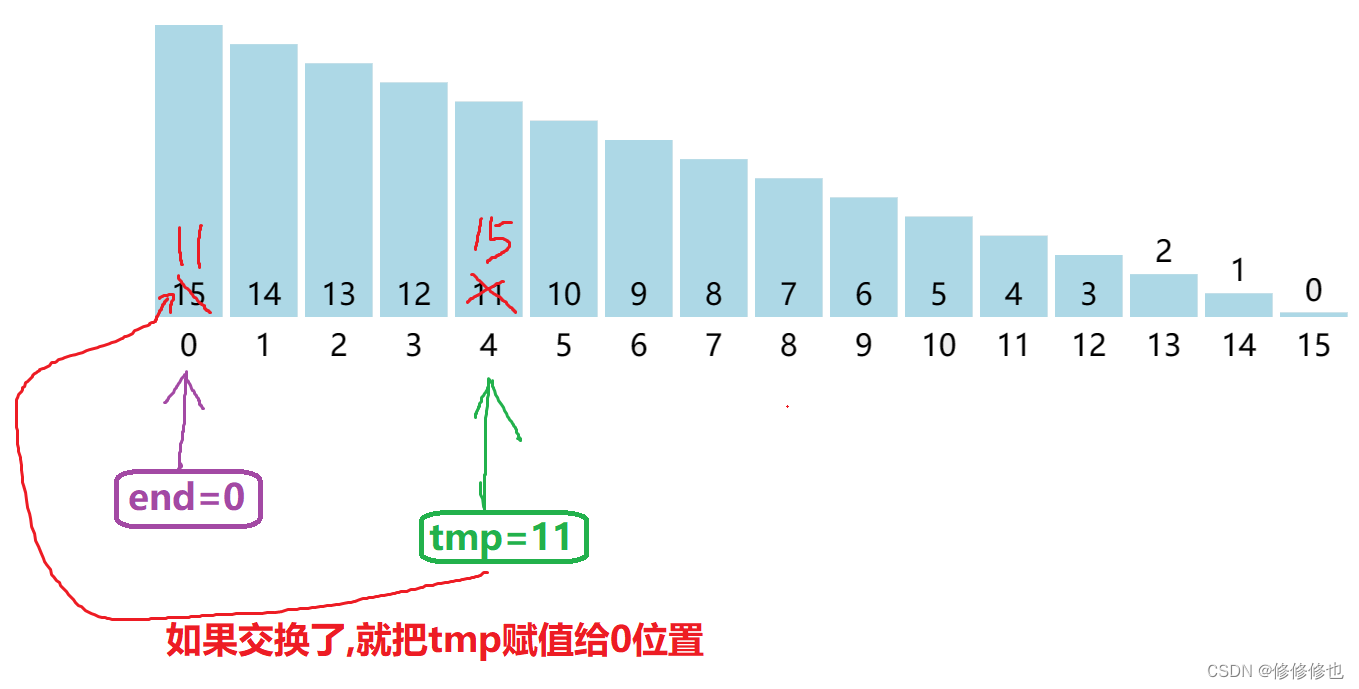
从下标为0的元素开始,遍历到下标为n-gap个元素为止,我们使用end来记录本次处理的元素下标,用tmp记录下间隔gap的元素的数值.
和间隔gap的两个元素进行比较,如果a[end+gap] < a[end],则将a[end]的值赋值给a[end+gap],并给end减掉gap.
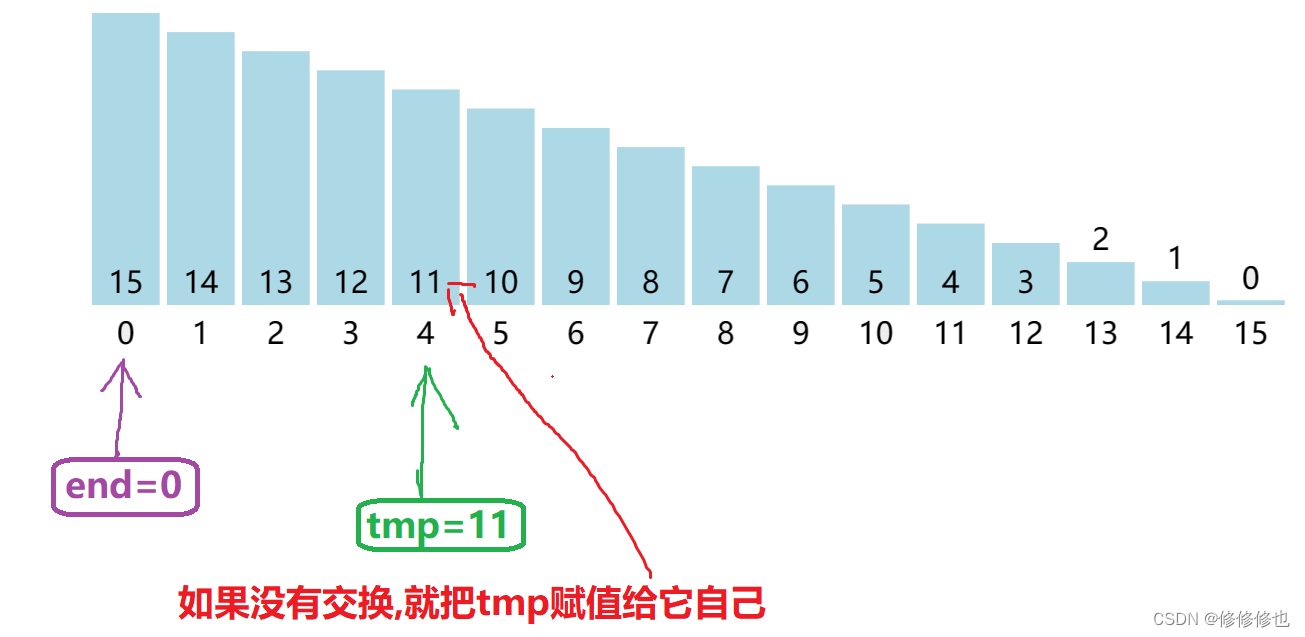
然后无论这次有没有交换位置,都将tmp赋值给a[end+gap]的位置,如果没有交换,则a[end+gap]就是tmp原本的值,如果这次有交换,则因为end减去了gap,则会使tmp赋值给原本a[end]的位置.该部分图示如下:
当第一轮遍历完下标为n-gap的元素之后,给gap除以2,继续重复1-3步的操作.
不断重复第4步操作,直到最终gap为1,即执行直接插入排序后,本次排序完成.

搞清算法实现步骤后,代码实现就比较简单了,希尔排序代码如下:

//希尔排序(升序
void ShellSort(int* a, int n)
{int gap = n;//gap>1都是在预排序//gap==1时就是直接插入排序了while (gap > 1){gap /= 2;//嫌慢的话可以gap/=3+1.加一是要保证最后一次一定是1for (int i = 0; i < n - gap; i++){int end = i;int tmp = a[i + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}
}

四.希尔排序算法的时间复杂度分析

希尔排序的时间复杂度的计算是较为复杂的,我们先来看两本官方书籍对该部分的描述:

       希尔排序的分析是一个复杂的问题，因为它的时间是所取“增量”序列的函数，这涉及一些数学上尚未解决的难题。因此，到目前为止尚未有人求得一种最好的增量序列，但大量的研究已得出一些局部的结论。如有人指出，当增量序列为 $dlta[k]=2^{t-k+1}-1$ 时，希尔排序的时间复杂度为 $O(n^{\frac{3}{2}})$ ，其中t为排序趟数， $1 \leqslant k \leqslant t \leqslant \left \lfloor log_{2}(n+1) \right \rfloor$ 。

        还有人在大量的实验基础上推出：当n在某个特定范围内，希尔排序所需的比较和移动次数约为 $n^{1.3}$ ，当 $n\rightarrow \infty$ 时，可减少到 $n((log_{2}n)^{2})^{2}$ 。增量序列可以有各种取法，但需注意：应使增量序列中的值没有除1之外的公因子，并且最后一个增量值必须等于1。

                                                                 ——《数据结构(C语言版)》严蔚敏

gap的取法有多种。最初Shell提出取 $gap=\left \lfloor \frac{n}{2} \right \rfloor$ ， $gap=\left \lfloor \frac{gap}{2} \right \rfloor$ ，直到gap=1,后来Knuth提出取 $gap=\left \lfloor \frac{gap}{3} \right \rfloor+1$ 。还有人提出都取奇数为好，也有人提出各gap互质为好。无论哪一种主张都没有得到证明。
对希尔排序的时间复杂度的分析很困难，在特定情况下可以准确地估算关键码的比较次数和对象移动次数，但想要弄清关键码比较数和对象移动次教与增量选择之间的依赖关系，并给出完整的数学分析，还没有人能够做到。在Knuth所著的《计算机程序设计技巧》第3卷中，利用大量的实验统计资料得出，当n很大时，关键码平均比较次数和对象平均移动次数大约在 $n^{1.25}$ 到 $1.6n^{1.25}$ 范围内，这是在利用直接插入排序作为子序列排序方法的情况下得到的。 ——《数据结构-用面向对象方法与C++描述》殷人昆

因此,当前对于希尔排序的时间复杂度,学术界仍没有一个确切的研究结果,我们只能在估算希尔排序时间复杂度时借助Knuth大佬的实验统计结果,即采用 $O(n^{1.25})$ 到 $O(1.6*n^{1.25})$ 来近似的估算希尔排序的时间复杂度.

结语

希望这篇希尔排序算法详解能对大家有所帮助,欢迎大佬们留言或私信与我交流.

有关更多排序相关知识可以移步:

【数据结构】八大排序算法https://blog.csdn.net/weixin_72357342/article/details/135038495?csdn_share_tail=%7B%22type%22%3A%22blog%22%2C%22rType%22%3A%22article%22%2C%22rId%22%3A%22135038495%22%2C%22source%22%3A%22weixin_72357342%22%7D&fromshare=blogdetail学海漫浩浩,我亦苦作舟!关注我,大家一起学习,一起进步!

相关文章推荐

【数据结构】八大排序之冒泡排序算法

【数据结构】八大排序之希尔排序算法

数据结构排序算法篇思维导图:

【数据结构】八大排序之希尔排序算法

🦄个人主页:修修修也 🎏所属专栏:数据结构 ⚙️操作环境:Visual Studio 2022 一.优化直接插入排序算法我们在之前对直接插入排序算法的优化部分通过对直接插入排序的分析可以得到一个结论,即: 进行直接插入排序的数组,如果越接近局部有序,则后续进行直…...

编程日记 2023/12/17 21:44:46

NestJS使用gRPC实现微服务通信

代码仓库地址：https://github.com/zeng-jc/rpc-grpc-practice 1.1 基本概念 gRPC 基于 Protocol Buffers（protobuf）作为接口定义语言（IDL），意味着你可以使用 protobuf 来定义你的服务接口，gRP…...

编程日记 2023/12/17 21:43:45

Android手机使用Termux终端模拟器

Termux 是 Android 平台上的一个终端模拟器，可以在 Android 手机上模拟 Linux 环境。它提供命令行界面，并且提供了功能健全的包管理工具（pkg）。另外就是 Termux 不需要 root 权限，安装后默认产生一个用户，可…...

编程日记 2023/12/17 21:42:45

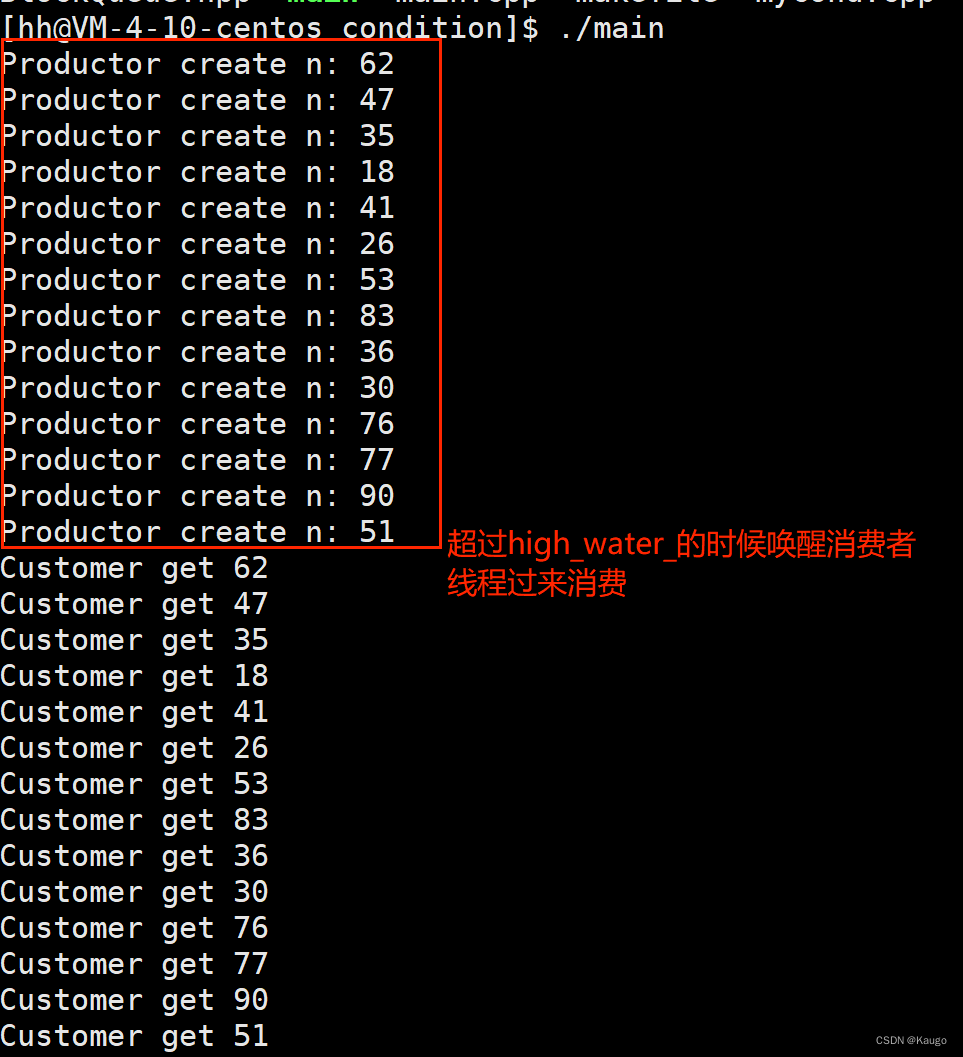
【Linux】cp问题，生产者消费者问题代码实现

文章目录前言一、 BlockQueue.hpp（阻塞队列）二、main.cpp 前言生产者消费者模式就是通过一个容器来解决生产者和消费者的强耦合问题。生产者和消费者彼此之间不直接通讯，而通过阻塞队列来进行通讯，所以生产者生产完数据之后不用…...

编程日记 2023/12/17 21:40:43

C++1114新标准——统一初始化（Uniform Initialization）、Initializer_list（初始化列表）、explicit

系列文章目录 C11&14新标准——Variadic templates（数量不定的模板参数） C11&14新标准——Uniform Initialization（统一初始化）、Initializer_list（初始化列表）、explicit 文章目录系列文章目录1…...

编程日记 2023/12/17 21:39:42

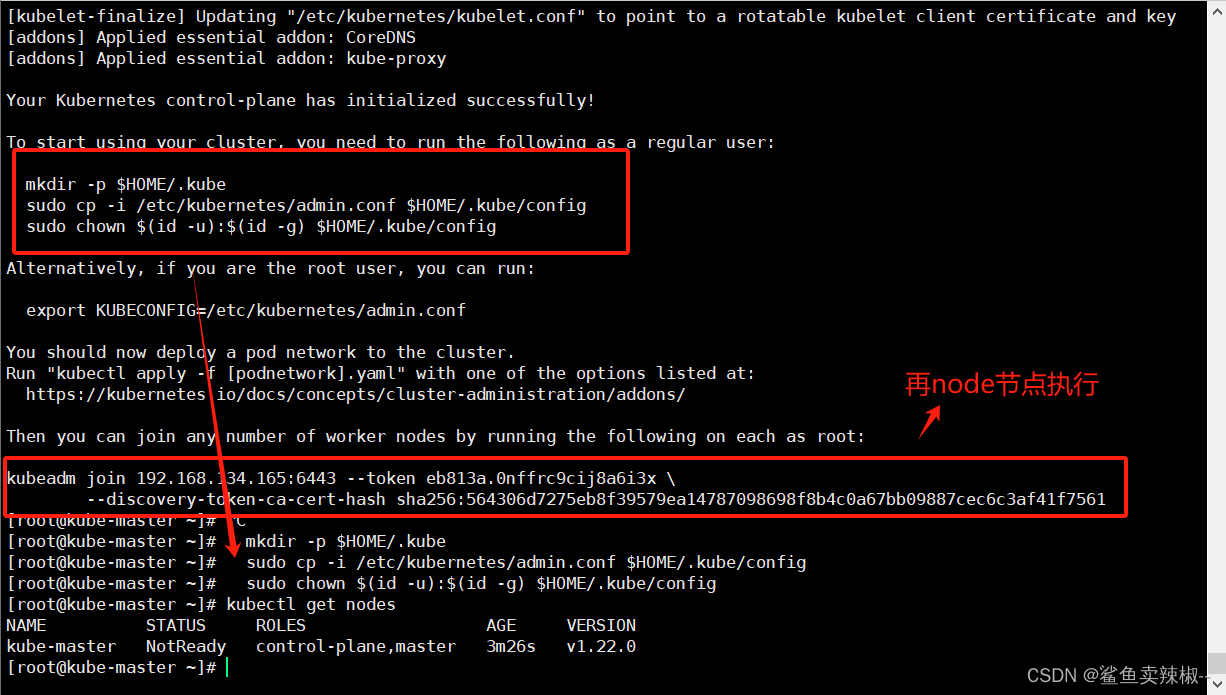
Kubeadm 方式部署K8s集群

环境主节点CPU核数必须是 ≥2核且内存要求必须≥2G，否则k8s无法启动主机名地址角色配置kube-master192.168.134.165主节点2核4Gkube-node1192..168.134.166 工作节点2核4Gkube-node2192.168.134.163工作节点2核4G 1.获取镜像谷歌镜像[由于国内网络原因…...

编程日记 2023/12/17 21:36:40

力扣376周赛

力扣第376场周赛找出缺失和重复的数字 map模拟 class Solution { public:vector<int> findMissingAndRepeatedValues(vector<vector<int>>& grid) {int n grid.size() , m grid[0].size();map<int,int>mi;for(int i 0 ; i < n ; i ){for…...

编程日记 2023/12/17 21:35:39

SU渲染受到电脑性能影响大吗？如何提高渲染速度

一般3d设计师们在进行设计工作前都需要提供一台高配电脑，那么你这知道su渲染对电脑要求高吗？电脑带不动su怎么解决？su对电脑什么配件要求高？今天这篇文章就详细为大家带来电脑硬件对su建模渲染的影响，以及su渲染慢怎么…...

编程日记 2023/12/17 21:33:38

Docker - Android源码编译与烧写

创建源代码并挂载到win目录 docker run -v /mnt/f/android8.0:/data/android8.0 -it --name android8.0 49a981f2b85f /bin/bash 使用 docker update 命令动态调整内存限制： 重新运行一个容器 docker run -m 512m my_container 修改运行中容器显示运行中容器 d…...

编程日记 2023/12/17 21:32:37

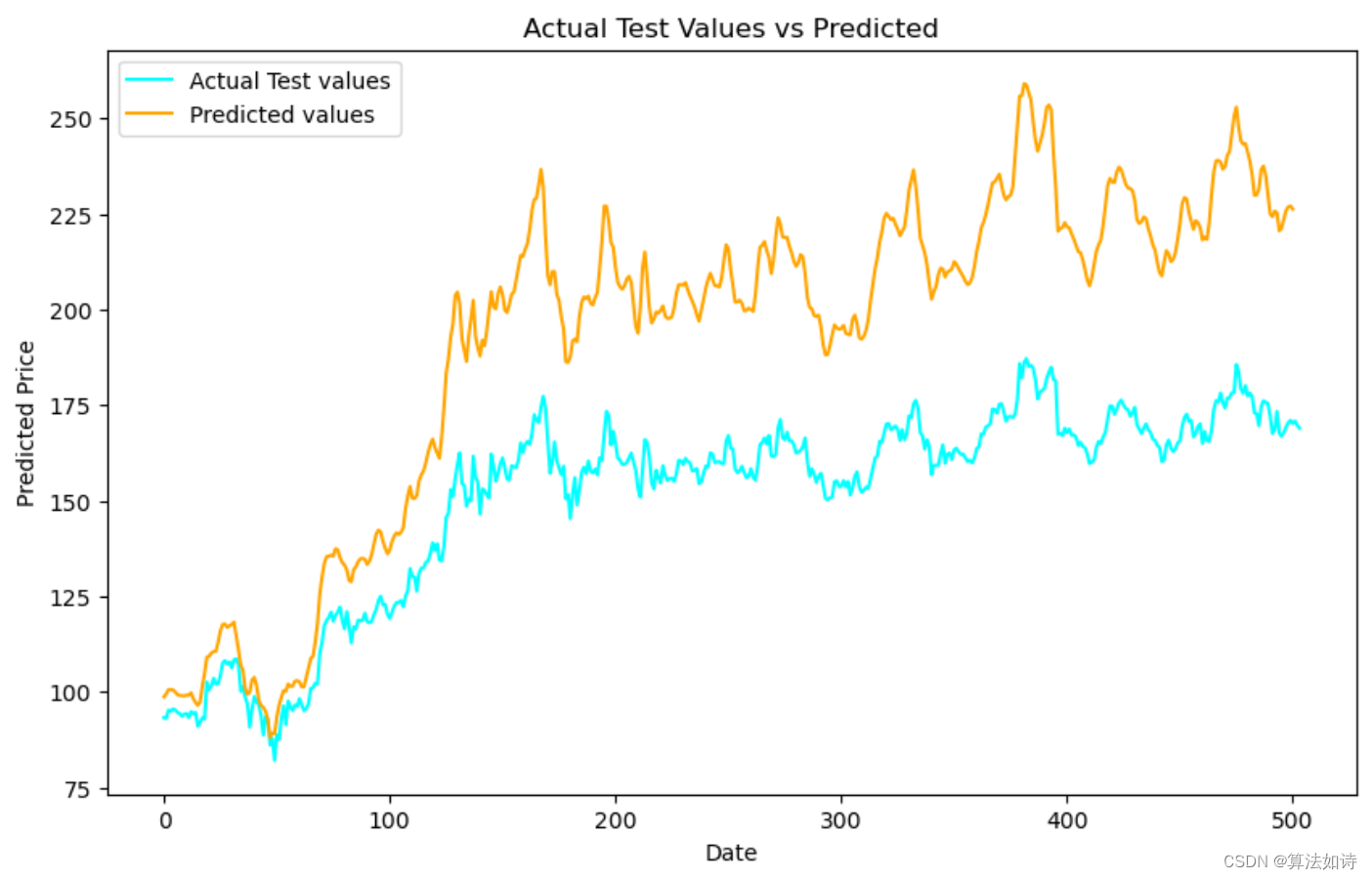
股票价格预测 | Python实现基于ARIMA和LSTM的股票预测模型（含XGBoost特征重要性衡量）

文章目录效果一览文章概述模型描述源码设计效果一览文章概述 Python实现基于ARIMA和LSTM的股票预测模型（Stock-Prediction） Data ExtractionFormatting data for time seriesFeature engineering（Feature Importance using X...

编程日记 2023/12/17 21:30:35

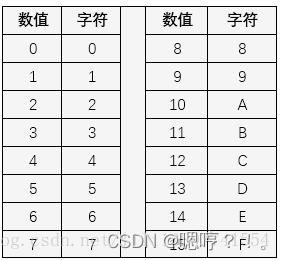
Base64

1. Base64是什么？ Base64（基底64）是一种基于64个可打印字符来表示二进制数据的表示方法。每6个比特为一个单元，对应某个可打印字符。3个字节相当于24个比特，对应于4个Base64单元，即3个字节可由4个可打印字…...

编程日记 2023/12/17 21:28:34

二叉搜索树的简单C++类实现

二叉搜索树（BST）是一种重要的数据结构，它对于理解树的操作和算法至关重要，其中序输出是有序的。本文通过C实现一个BST的类，并在插入和删除节点时提供清晰的输出，可视化这些操作的过程。二叉搜索树的节点结…...

编程日记 2023/12/17 21:26:32

禁毒知识竞赛流程和规则

禁毒知识竞赛是一项全国性竞赛活动。有着深化全国青少年毒品预防教育，巩固学校毒品预防教育成果的重要作用。本文介绍一场禁毒知识竞赛的完整流程和规则，供单位组织此类活动时参考。 1、赛制第一轮10进6，第二轮6进4，4支队伍决出…...

编程日记 2023/12/17 21:25:31

CSS 基础

文章目录 CSS 常见的属性CSS 常见样式行内样式内嵌样式导入样式 CSS 选择器标签选择器id选择器类选择器全局选择器属性选择器组合选择器 CSS 常见应用表格列表导航栏下拉菜单提示工具图片廊 CSS (Cascading Style Sheets，层叠样式表），是一种用…...

编程日记 2023/12/17 21:22:29

黑色翻页时钟HTML源码-倒计时单页翻页时钟

黑色翻页时钟HTML源码-倒计时单页翻页时钟这是一个类似fliqlo的黑色翻页时钟HTML源码，它仅包含一个HTML文件，上传到网站后即可使用。该时钟具有查看当前时间、秒表和倒计时功能，并且可以在页面的右下角进行设置。红色动态炫酷数字时钟html网…...

编程日记 2023/12/17 21:21:27

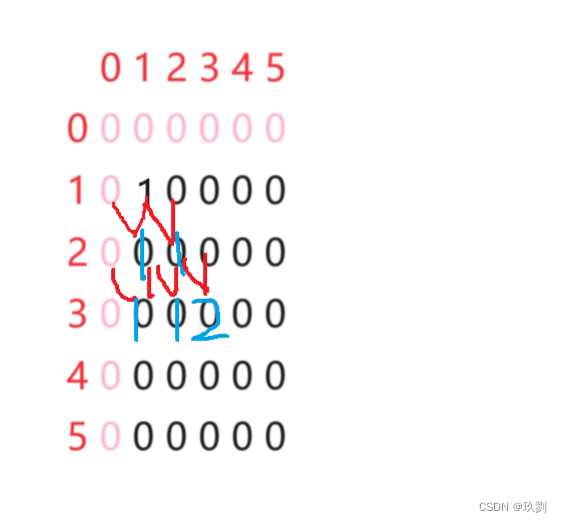
2043杨辉三角（C语言）

目录一：题目二：思路分析三：代码一：题目二：思路分析 1.通过杨辉三角，不难发现中间的数等于肩头两个数之和 2.但是当我们的输出结果，与杨辉三角的形式有所不同，但是我们可以找…...

编程日记 2023/12/17 21:19:26

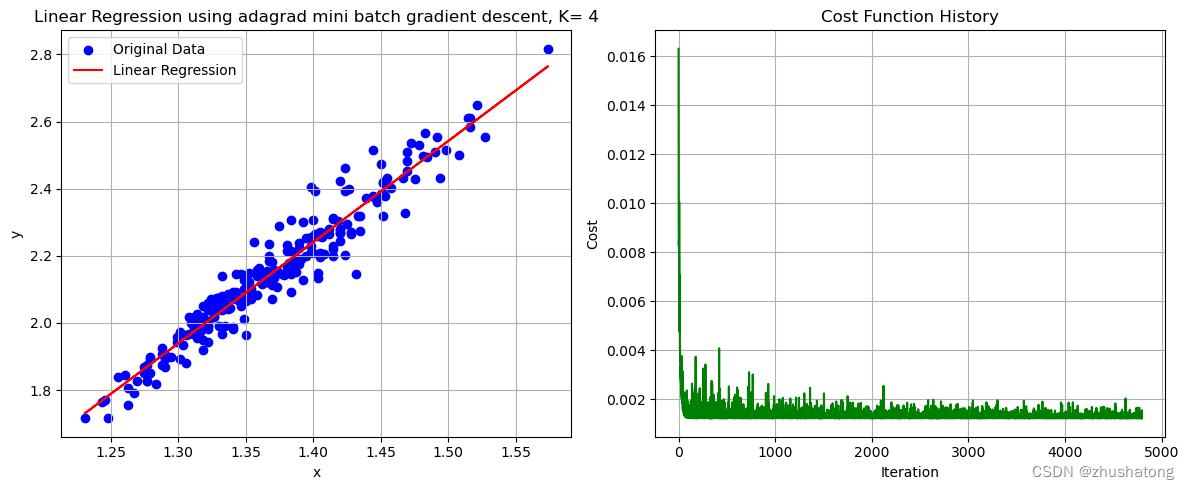
【机器学习】从底层手写实现线性回归

【机器学习】Building-Linear-Regression-from-Scratch 线性回归 Linear Regression0. 数据的导入与相关预处理0.工具函数1. 批量梯度下降法 Batch Gradient Descent2. 小批量梯度下降法 Mini Batch Gradient Descent（在批量方面进行了改进）3. 自适应梯度…...

编程日记 2023/12/17 21:18:25

判断数组中对象的某个值是否有相同的并去重

如果你想判断数组中对象的某个值是否有相同的，并进行去重，你可以使用 JavaScript 中的一些数组方法和 Set 对象。以下是一个示例： // 原始数组包含对象 const array [{ id: 1, name: John },{ id: 2, name: Jane },{ id: 3, name: Doe },{ …...

编程日记 2023/12/17 21:17:23

Shell脚本变量语句表达式

常见的解释器 #!/bin/sh #不推荐(了解) #!/bin/bash #!/usr/bin/python #!/bin/awk#!后跟的字符表示要启动的程序，该程序读取该文件执行。 #! 是一个约定的标记，它告诉系统这个脚本需要什么解释器来执行shell 函数 myShellName () {command1 }函数调用…...

编程日记 2023/12/17 21:16:22

MIT6.S081-实验准备

实验全程在Vmware虚拟机 (镜像：Ubuntu-20.04-beta-desktop-amd64) 中进行一、版本控制 1.1 将mit的实验代码克隆到本地 git clone git://g.csail.mit.edu/xv6-labs-2020 1.2 修改本地git配置文件创建github仓库，记录仓库地址我的仓库地址就是htt…...

编程日记 2023/12/17 21:14:20

工具在手，创作无忧：一键下载安装Auto CAD工具，让艺术创作更加轻松愉悦！

不要再浪费时间在网上寻找Auto CAD的安装包了！因为你所需的一切都可以在这里找到！作为全球领先的设计和绘图软件，Auto CAD为艺术家、设计师和工程师们提供了无限的创作潜力。不论是建筑设计、工业设计还是室内装饰，Auto CAD都能助…...

编程日记 2023/12/17 21:12:18

第25节: Vue3 带组件

在UniApp中使用Vue3框架时，你可以使用组件来封装可复用的代码块，并在需要的地方进行渲染。下面是一个示例，演示了如何在UniApp中使用Vue3框架使用带组件： <template> <view> <button click"toggleActive&q…...

编程日记 2023/12/17 21:08:15

ubuntu apache2配置反向代理

1.Ubuntu安装apache sudo apt-get update sudo apt-get install apache2 2.apache2反向代理配置 sudo vim /etc/apache2/sites-available/000-default.conf 添加内容如下： <VirtualHost *:80># The ServerName directive sets the request scheme, host…...

编程日记 2023/12/17 21:07:14

【数据挖掘 | 关联规则】FP-grow算法详解（附详细代码、案例实战、学习资源）

! 🤵‍♂️ 个人主页: AI_magician 📡主页地址： 作者简介：CSDN内容合伙人，全栈领域优质创作者。 👨‍💻景愿：旨在于能和更多的热爱计算机的伙伴一起成长！！&a…...

编程日记 2023/12/17 21:05:12

力扣题目学习笔记(OC + Swift) 11

11.盛最多水的容器给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。返回容器可以储存的最大水量。说明：你不能倾…...

编程日记 2023/12/17 21:04:11

JVM基础入门

JVM 基础入门 JVM 基础聊一聊 Java 从编码到执行到底是一个怎么样的过程？ 假设我们有一个文件 x.Java，你执行 javac，它就会变成 x.class。这个 class 怎么执行的？ 当我们调用 Java 命令的时候，class 会被 load 到…...

编程日记 2023/12/17 21:02:09

前端真的死了吗

随着人工智能和低代码的崛起，“前端已死”的声音逐渐兴起。前端已死？尊嘟假嘟？快来发表你的看法吧！ 以下方向仅供参考。一、为什么会出现“前端已死”的言论前端已死这个言论是出自于2022年开始 ，2022年下半年疫情…...

编程日记 2023/12/17 20:59:07

前后端分离开发

前期前后端混合开发后期前后端分离开发...

编程日记 2023/12/17 20:57:06

向量数据库——AI时代的基座

向量数据库——AI时代的基座 1.前言向量数据库在构建基于大语言模型的行业智能应用中扮演着重要角色。大模型虽然能回答一般性问题，但在垂直领域服务中，其知识深度、准确度和时效性有限。为了解决这一问题，企业可以利用向量数据库结合大模…...

编程日记 2023/12/17 20:55:04

【️什么是分布式系统的一致性？】

😊引言 🎖️本篇博文约8000字，阅读大约30分钟，亲爱的读者，如果本博文对您有帮助，欢迎点赞关注！😊😊😊 🖥️什么是分布式系统的一致性 &#xff1f…...

编程日记 2023/12/17 20:54:02

洛阳疾控最新通告今天/seo官网优化怎么做

1、标识符由字母、数字、下划线组成；2、标识符不能以数字开头；3、标识符区分大小写；PS:以下划线开头的标识符具有特殊意义： 以单下划线开头 （如_init） 为不能直接访问的类属性，必须通过类提供的…...

编程日记 2025/1/12 7:39:48

网站建设免费加盟代理/小程序运营推广公司

近期服务器不太稳定。。电信方面有点无暇顾及此处。。所以。。我的网站也要遭殃了一段时间咯！转载于:https://www.cnblogs.com/tataa/archive/2004/08/24/36193.html...

编程日记 2025/1/12 6:57:55

wordpress上传录音/所有关键词

CAD审图标记最新版是一款功能强大的cad审图软件。CAD审图标记免费版将图片中的细节进行重点标注,轻松帮助CAD制图人员进行修改。使用CAD审图标记最新版大大提高工作效率,SmartMark是一款免费cad审图软件,软件能够帮助用户在审图的过程中,标注下自己的审图意见,方便用户在下次修…...

编程日记 2025/1/12 6:48:49

成立公司注册资金可以随便写吗/百度seo新规则

内容出自极客时间专栏《Linux 性能优化实战》 CPU 的性能指标那么多，CPU 性能分析工具一抓一大把，换成实际的工作场景，该观察什么指标、选择哪个性能工具呢？ 不要担心，今天我就以多年的性能优化经验，为你总…...

编程日记 2025/1/12 2:37:22

软件开发网页设计网站/网站底部友情链接代码

容器是一个打包了应用和服务的环境，是一个轻量级的虚拟机，每一个容器都由一组特定的应用和必要的依赖库组成。容器的管理操作容器常见的命令：查看、创建、启动、终止和删除创建容器 docker create docker run 二者的区别在于docker create…...

编程日记 2025/1/11 23:49:50

网站建设分录/线上营销模式

定义结构为了定义结构，您必须使用 struct 语句。struct 语句定义了一个包含多个成员的新的数据类型，struct 语句的格式如下： struct type_name { member_type1 member_name1; member_type2 member_name2; member_type3 member_name3; . . …...

编程日记 2025/1/11 23:27:57

一.优化直接插入排序算法

二.希尔排序简介及思路

三.希尔排序算法的代码实现

四.希尔排序算法的时间复杂度分析

结语

相关文章：