2043杨辉三角(C语言)
目录
一:题目
二:思路分析
三:代码
一:题目
二:思路分析
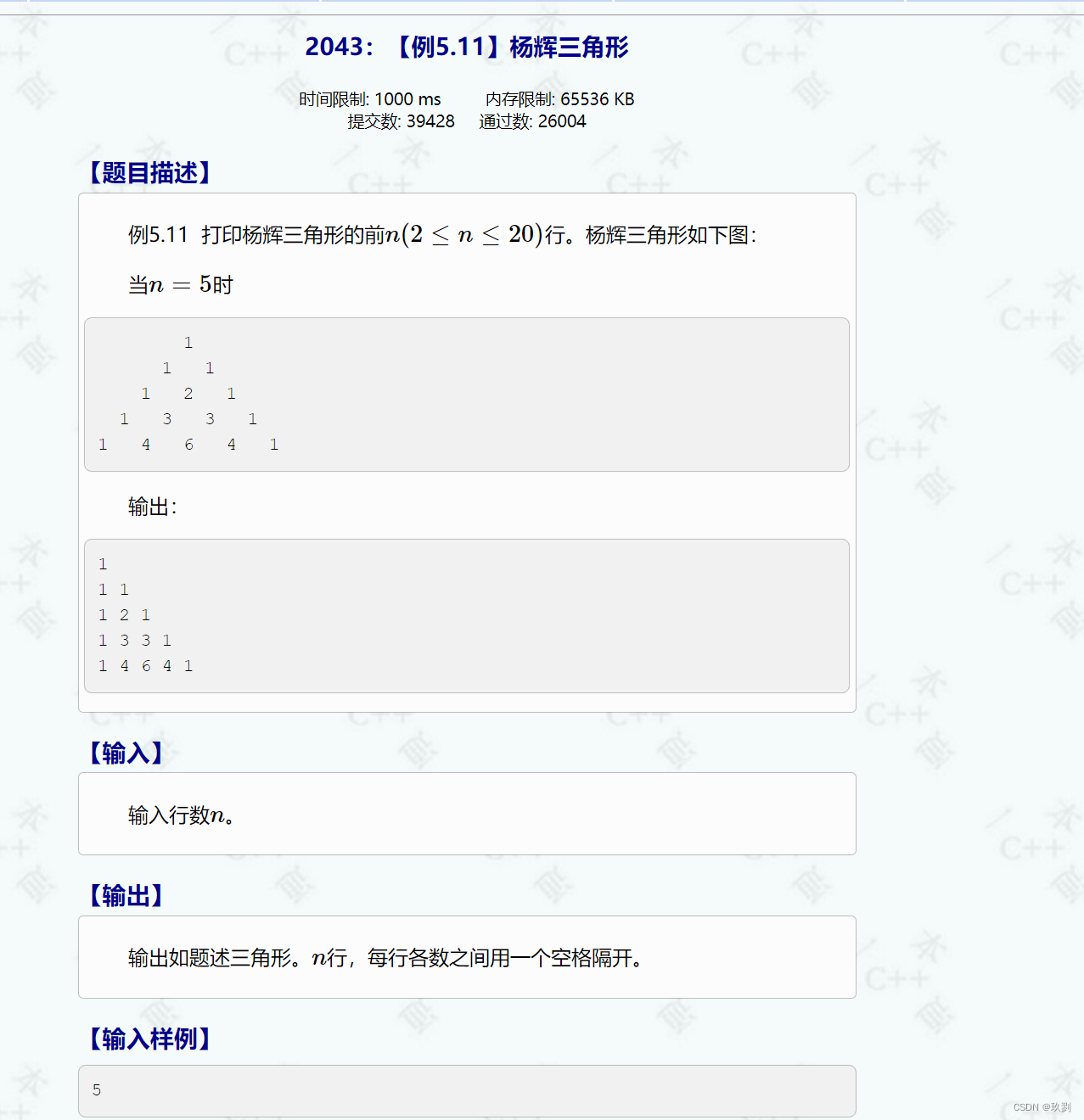
1.通过杨辉三角,不难发现中间的数等于肩头两个数之和

2.但是当我们的输出结果,与杨辉三角的形式有所不同,但是我们可以找到与杨辉三角相似的规律,即一个数等于上面的数和上面数的右边的的数的和(arr[i][j] = arr[i-1][j]+arr[i-1][j-1])

3.这是又出现一个问题,如何用代码实现呢?我们只是找到了规律,但是如何应用规律呢?我们怎么赋值呢?
不难看出第一列和最后一个数都是1,那我们要把这两种情况单独拿出来讨论,将它们赋值为1吗?
这稍微有一点麻烦。
这时,不妨看一下我对杨辉三角第一行和第二行的理解,将它们理解为第一行的两边还有一个未显示的0,第二行的1是由第一行的1+0得到的,同理假设我们求的是五行杨辉三角,那么第二行的1是由第一行的1和它右边的0相加得到的,但是如果求五行,我们创建的是5*5的二维数组的话,第一行的1是第一行开始的数,如果访问它右边的数就越界了,所以这是不妨扩建数组为6*6的。

在这个基础上,我们只要把(1,1)处的值赋为1,再带入我们找到的规律,就可以得到结果了

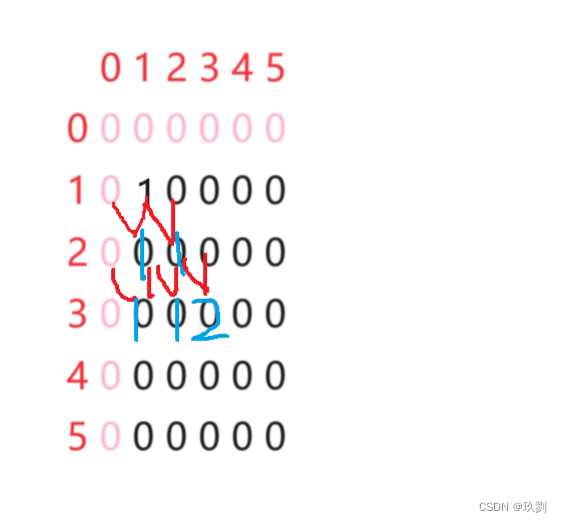
4.对于杨辉三角,第i行有i个数,所以循环时i的范围是1~n,而j的范围是1~i
三:代码
#include <stdio.h>
//2043杨辉三角
int main()
{int n = 0;scanf("%d", &n);int arr[21][21] = { 0 };int i = 0, j =0;for (i = 1; i <= n; i++)//0~n{for (j = 1; j <= n; j++){if (i == 1 && j == 1)arr[i][j] = 1;elsearr[i][j] = arr[i - 1][j] + arr[i - 1][j - 1];}}for (i = 1; i <= n; i++){for (j = 1; j <= i; j++){printf("%d ", arr[i][j]);}printf("\n");}return 0;
}相关文章:

2043杨辉三角(C语言)
目录 一:题目 二:思路分析 三:代码 一:题目 二:思路分析 1.通过杨辉三角,不难发现中间的数等于肩头两个数之和 2.但是当我们的输出结果,与杨辉三角的形式有所不同,但是我们可以找…...
【机器学习】从底层手写实现线性回归
【机器学习】Building-Linear-Regression-from-Scratch 线性回归 Linear Regression0. 数据的导入与相关预处理0.工具函数1. 批量梯度下降法 Batch Gradient Descent2. 小批量梯度下降法 Mini Batch Gradient Descent(在批量方面进行了改进)3. 自适应梯度…...

判断数组中对象的某个值是否有相同的并去重
如果你想判断数组中对象的某个值是否有相同的,并进行去重,你可以使用 JavaScript 中的一些数组方法和 Set 对象。以下是一个示例: // 原始数组包含对象 const array [{ id: 1, name: John },{ id: 2, name: Jane },{ id: 3, name: Doe },{ …...

Shell脚本 变量 语句 表达式
常见的解释器 #!/bin/sh #不推荐(了解) #!/bin/bash #!/usr/bin/python #!/bin/awk#!后跟的字符表示要启动的程序,该程序读取该文件执行。 #! 是一个约定的标记,它告诉系统这个脚本需要什么解释器来执行shell 函数 myShellName () {command1 }函数调用…...
MIT6.S081-实验准备
实验全程在Vmware虚拟机 (镜像:Ubuntu-20.04-beta-desktop-amd64) 中进行 一、版本控制 1.1 将mit的实验代码克隆到本地 git clone git://g.csail.mit.edu/xv6-labs-2020 1.2 修改本地git配置文件 创建github仓库,记录仓库地址 我的仓库地址就是htt…...

工具在手,创作无忧:一键下载安装Auto CAD工具,让艺术创作更加轻松愉悦!
不要再浪费时间在网上寻找Auto CAD的安装包了!因为你所需的一切都可以在这里找到!作为全球领先的设计和绘图软件,Auto CAD为艺术家、设计师和工程师们提供了无限的创作潜力。不论是建筑设计、工业设计还是室内装饰,Auto CAD都能助…...

第25节: Vue3 带组件
在UniApp中使用Vue3框架时,你可以使用组件来封装可复用的代码块,并在需要的地方进行渲染。下面是一个示例,演示了如何在UniApp中使用Vue3框架使用带组件: <template> <view> <button click"toggleActive&q…...

ubuntu apache2配置反向代理
1.Ubuntu安装apache sudo apt-get update sudo apt-get install apache2 2.apache2反向代理配置 sudo vim /etc/apache2/sites-available/000-default.conf 添加内容如下: <VirtualHost *:80># The ServerName directive sets the request scheme, host…...

【数据挖掘 | 关联规则】FP-grow算法详解(附详细代码、案例实战、学习资源)
! 🤵♂️ 个人主页: AI_magician 📡主页地址: 作者简介:CSDN内容合伙人,全栈领域优质创作者。 👨💻景愿:旨在于能和更多的热爱计算机的伙伴一起成长!!&a…...
 11)
力扣题目学习笔记(OC + Swift) 11
11.盛最多水的容器 给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。 找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。 返回容器可以储存的最大水量。 说明:你不能倾…...
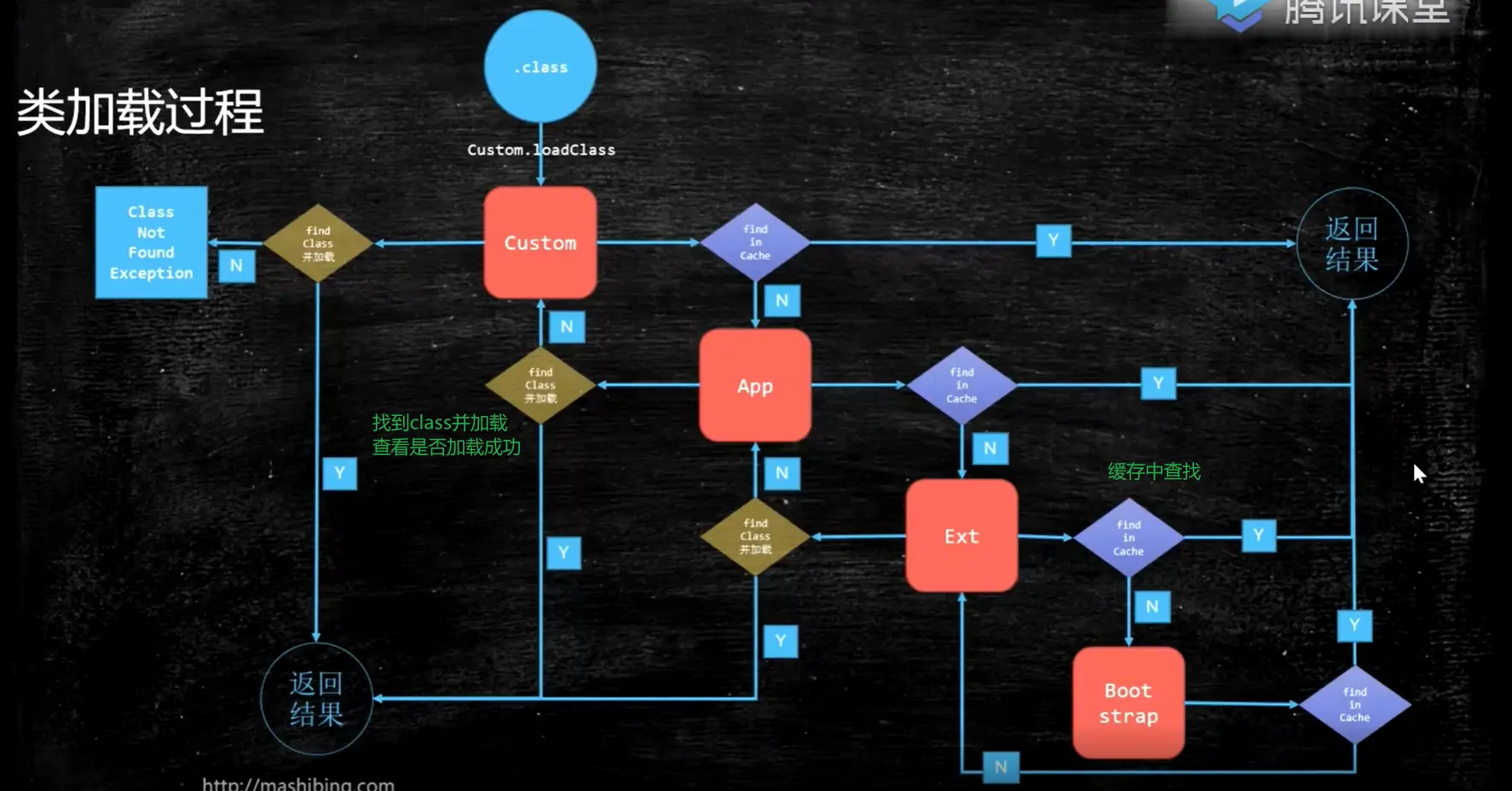
JVM基础入门
JVM 基础入门 JVM 基础 聊一聊 Java 从编码到执行到底是一个怎么样的过程? 假设我们有一个文件 x.Java,你执行 javac,它就会变成 x.class。 这个 class 怎么执行的? 当我们调用 Java 命令的时候,class 会被 load 到…...

前端真的死了吗
随着人工智能和低代码的崛起,“前端已死”的声音逐渐兴起。前端已死?尊嘟假嘟?快来发表你的看法吧! 以下方向仅供参考。 一、为什么会出现“前端已死”的言论 前端已死这个言论 是出自于2022年开始 ,2022年下半年疫情…...

前后端分离开发
前期 前后端混合开发 后期 前后端分离开发...
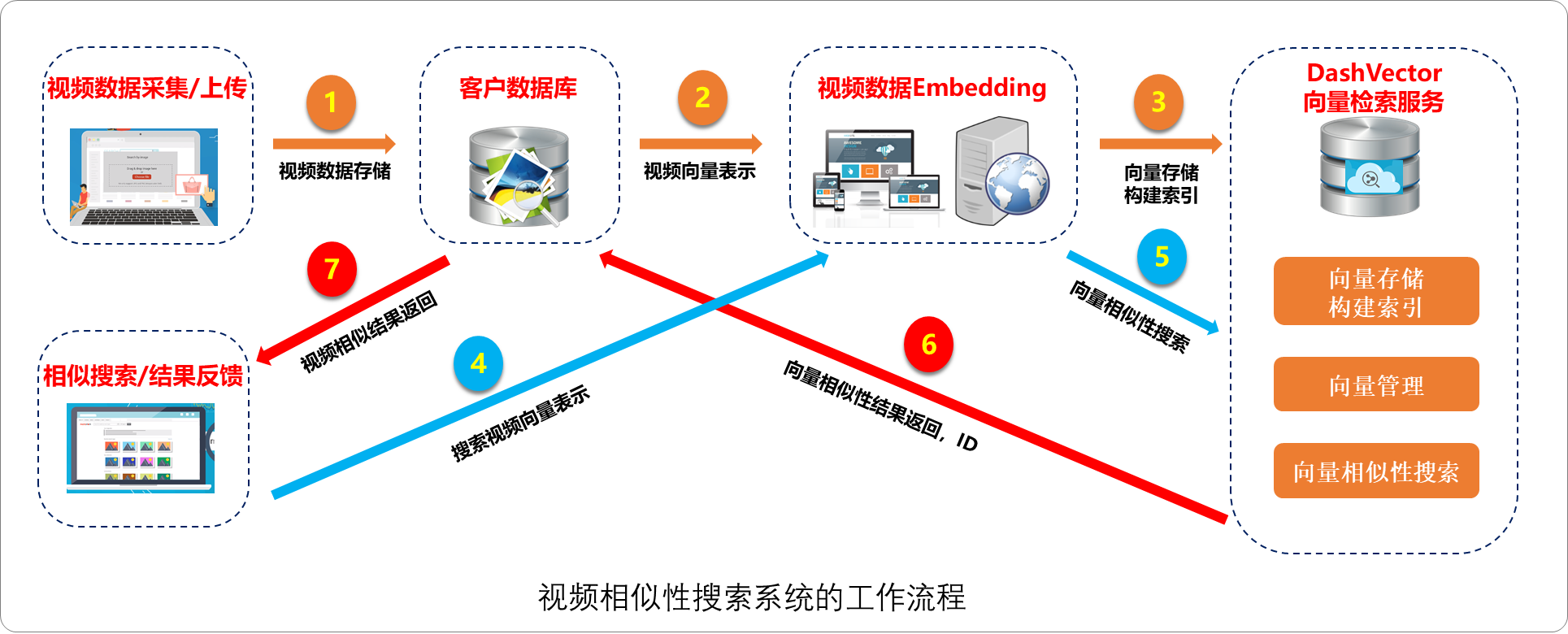
向量数据库——AI时代的基座
向量数据库——AI时代的基座 1.前言 向量数据库在构建基于大语言模型的行业智能应用中扮演着重要角色。大模型虽然能回答一般性问题,但在垂直领域服务中,其知识深度、准确度和时效性有限。为了解决这一问题,企业可以利用向量数据库结合大模…...

【️什么是分布式系统的一致性 ?】
😊引言 🎖️本篇博文约8000字,阅读大约30分钟,亲爱的读者,如果本博文对您有帮助,欢迎点赞关注!😊😊😊 🖥️什么是分布式系统的一致性 ?…...

鸿蒙ArkTS Web组件加载空白的问题原因及解决方案
问题症状 初学鸿蒙开发,按照官方文档Web组件文档《使用Web组件加载页面》示例中的代码照抄运行后显示空白,纠结之余多方搜索后扔无解决方法。 运行代码 import web_webview from ohos.web.webviewEntry Component struct Index {controller: web_webv…...
【Java】网络编程-UDP回响服务器客户端简单代码编写
这一篇文章我们将讲述网络编程中UDP服务器客户端的编程代码 1、前置知识 UDP协议全称是用户数据报协议,在网络中它与TCP协议一样用于处理数据包,是一种无连接的协议。 UDP的特点有:无连接、尽最大努力交付、面向报文、没有拥塞控制 本文讲…...

【设计模式】之工厂模式
工厂模式 1.介绍 工厂模式(创建型模式),是我们最常用的实例化对象模式,是用工厂方法代替new操作的一种模式;在工厂模式中,我们在创建对象时不会对客户端暴露创建逻辑,并且是通过使用一个共同的…...

70.爬楼梯
题目描述 假设你正在爬楼梯。需要 n 阶你才能到达楼顶。 每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢? 注意: 给定 n 是一个正整数。 示例 1: 输入: 2 输出: 2 解释: 有两种方法可以爬到楼顶…...

【论文解读】ICLR 2024高分作:ViT需要寄存器
来源:投稿 作者:橡皮 编辑:学姐 论文链接:https://arxiv.org/abs/2309.16588 摘要: Transformer最近已成为学习视觉表示的强大工具。在本文中,我们识别并表征监督和自监督 ViT 网络的特征图中的伪影。这些…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

VisualXML全新升级 | 新增数据库编辑功能
VisualXML是一个功能强大的网络总线设计工具,专注于简化汽车电子系统中复杂的网络数据设计操作。它支持多种主流总线网络格式的数据编辑(如DBC、LDF、ARXML、HEX等),并能够基于Excel表格的方式生成和转换多种数据库文件。由此&…...

Spring Boot + MyBatis 集成支付宝支付流程
Spring Boot MyBatis 集成支付宝支付流程 核心流程 商户系统生成订单调用支付宝创建预支付订单用户跳转支付宝完成支付支付宝异步通知支付结果商户处理支付结果更新订单状态支付宝同步跳转回商户页面 代码实现示例(电脑网站支付) 1. 添加依赖 <!…...
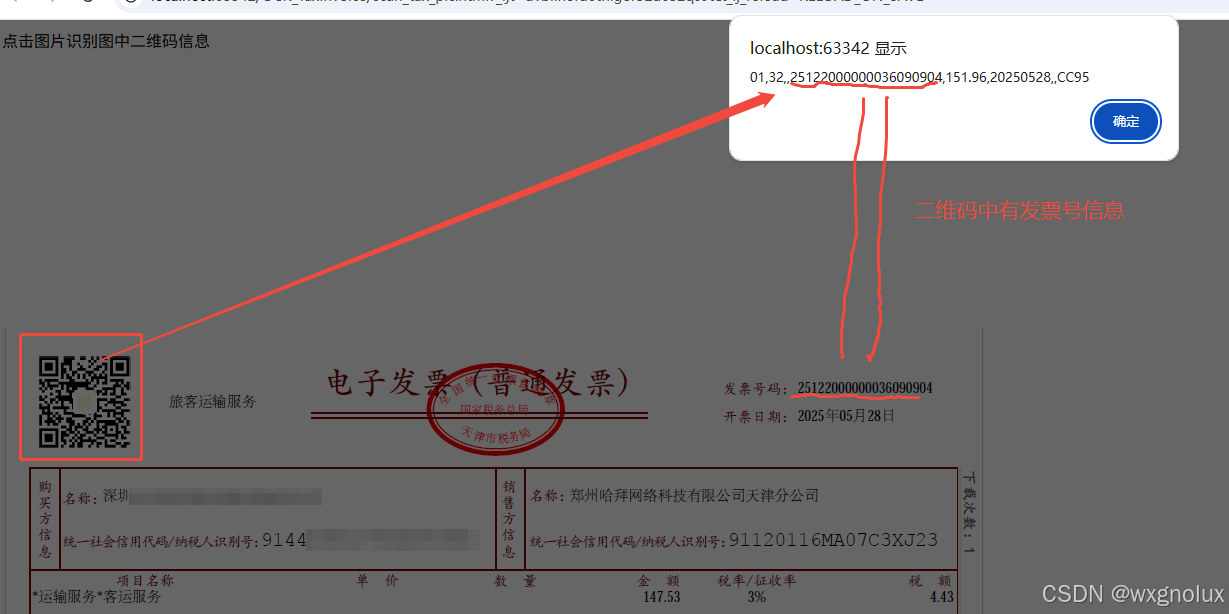
网页端 js 读取发票里的二维码信息(图片和PDF格式)
起因 为了实现在报销流程中,发票不能重用的限制,发票上传后,希望能读出发票号,并记录发票号已用,下次不再可用于报销。 基于上面的需求,研究了OCR 的方式和读PDF的方式,实际是可行的ÿ…...

英国云服务器上安装宝塔面板(BT Panel)
在英国云服务器上安装宝塔面板(BT Panel) 是完全可行的,尤其适合需要远程管理Linux服务器、快速部署网站、数据库、FTP、SSL证书等服务的用户。宝塔面板以其可视化操作界面和强大的功能广受国内用户欢迎,虽然官方主要面向中国大陆…...

Cursor AI 账号纯净度维护与高效注册指南
Cursor AI 账号纯净度维护与高效注册指南:解决限制问题的实战方案 风车无限免费邮箱系统网页端使用说明|快速获取邮箱|cursor|windsurf|augment 问题背景 在成功解决 Cursor 环境配置问题后,许多开发者仍面临账号纯净度不足导致的限制问题。无论使用 16…...
