12.4~12.14概率论复习与相应理解(学习、复习、备考概率论,这一篇就够了)
未分配的题目
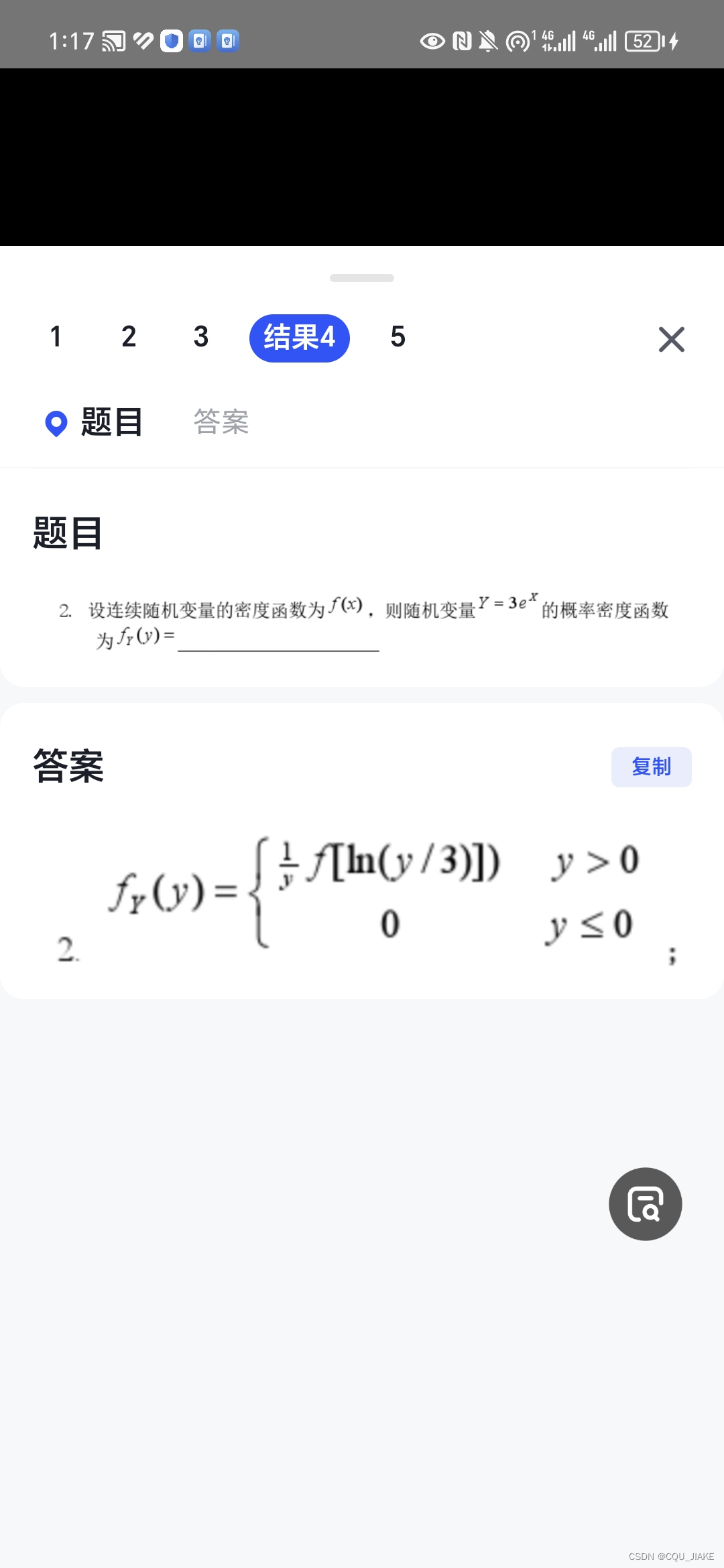
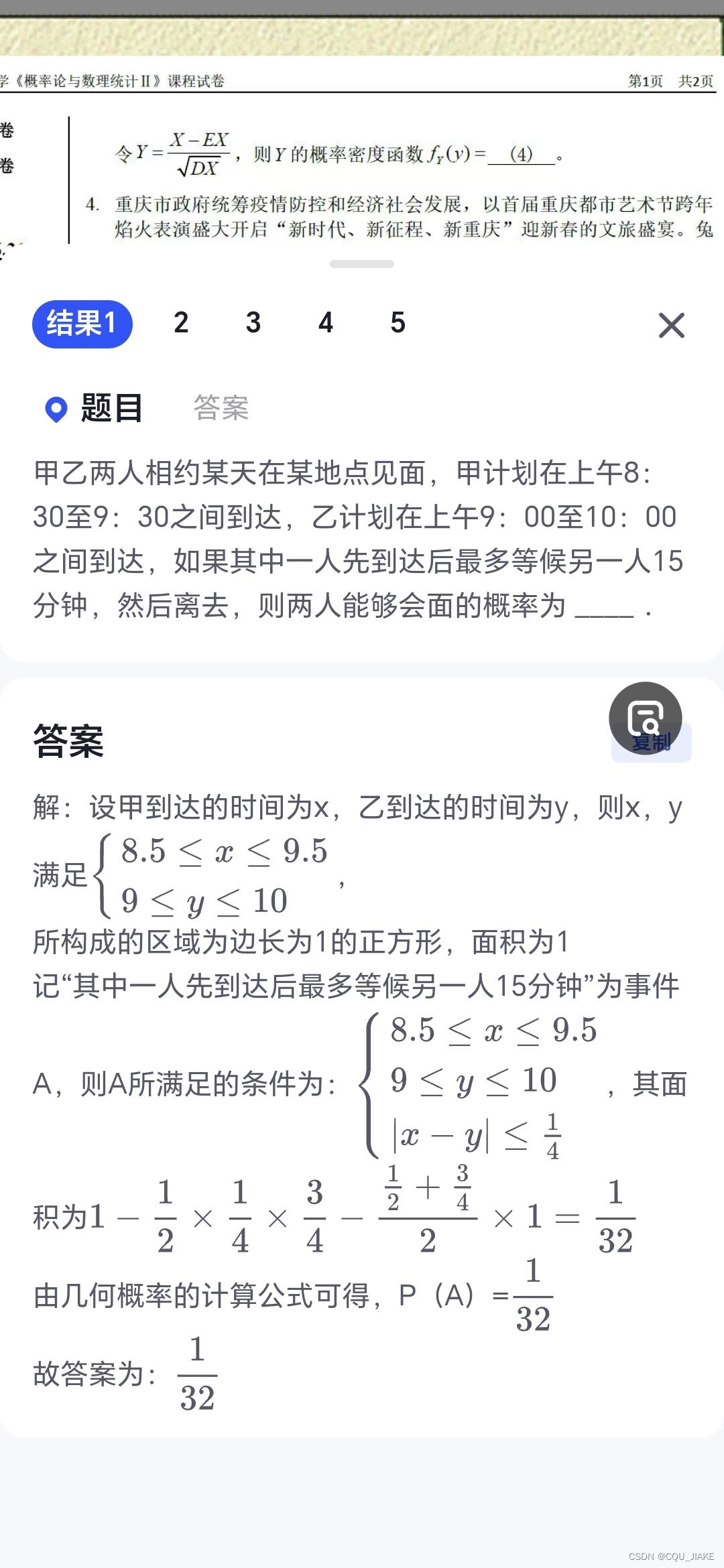




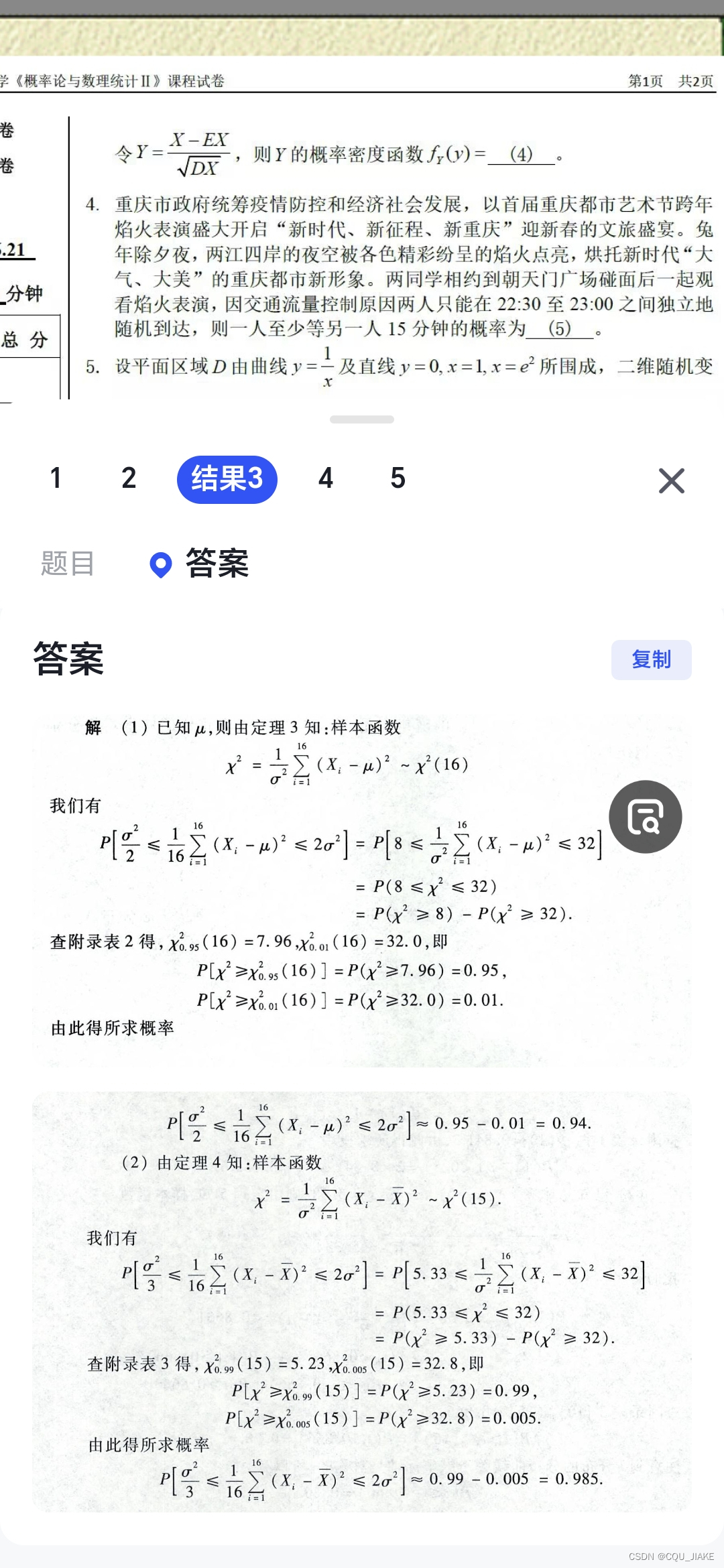




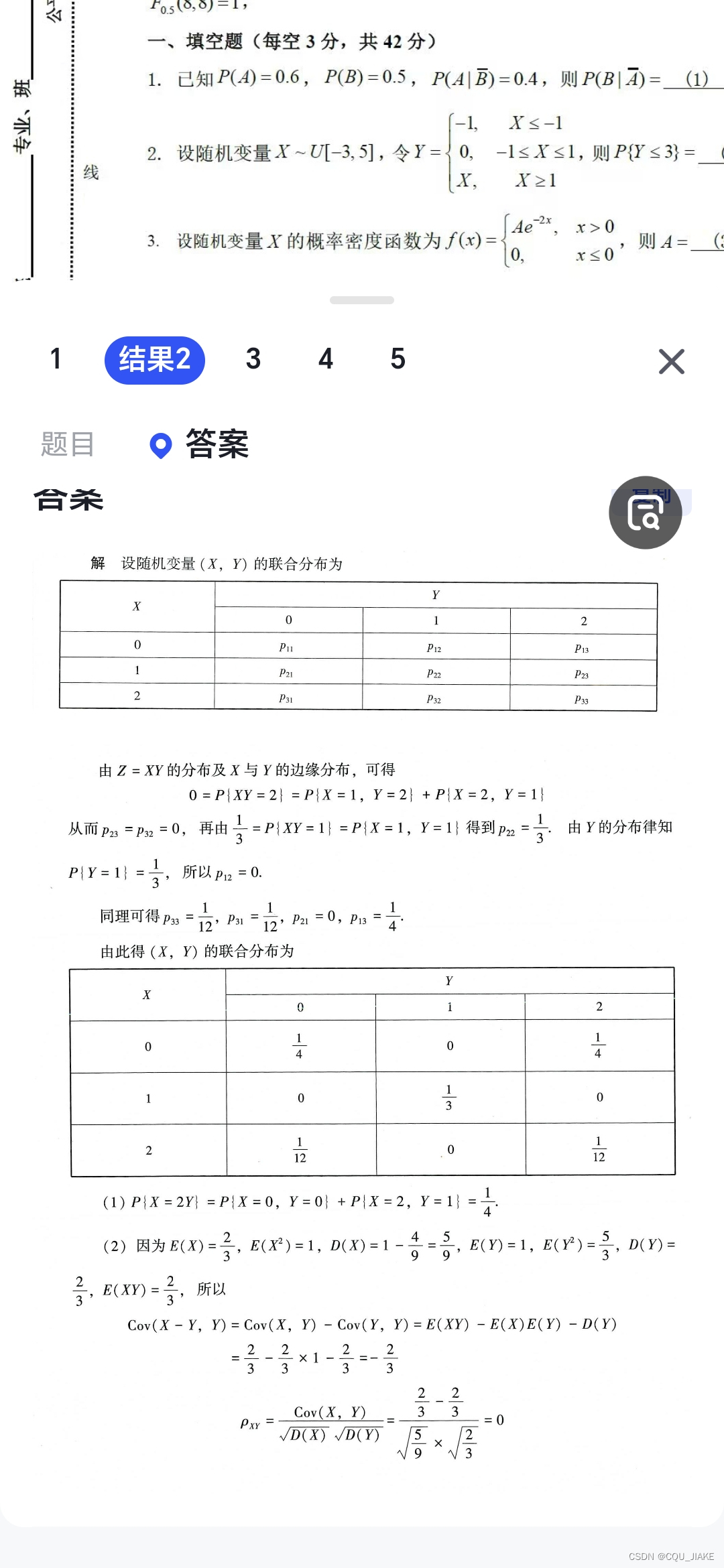




概率计算(一些转换公式与全概率公式)与实际概率 ,贝叶斯
一些转换公式











相关性质计算
常规,公式的COV与P
复习相关公式

计算出新表达式的均值,方差,再套正态分布的公式
![]()
COV的运算性质
如果两变量独立,那么EXY=EXEY
算COVXY,就是EXY-EXEY

E(X[X]),对于带绝对值的均值,直接进行积分,利用积分的对称关系求解
期望表达式中的式子,就是每个点对应的函数式的值。

面积为ΠR^2,派为常数,所以面积的期望取决于X^2的期望,方差取决于X^2的方差
COV(S,C)最终可化简为COV(R,R^2)=E(R*R^2)-E(R)E(R^2)
X^2的方差,计算一下X^4的积分,一共要算X^3,X^4两个积分

对于此类型的X,Y变化,满足变化后的量,均值为0,方差为1
奇怪,不规则的COV,P
一般就是离散的二维变量X,Y。核心就是依据题目特点,写出X,Y的离散分布表,然后就计算,EXY,EX,EY,EX^2,EY^2,DX,DY等关键数据
即主要是考分布律的求解


联合分布律,直接联合各变量可能出现的所有离散值列表,然后分别计算格子上各种情况的概率,就变得一目了然了

直接依照各变量可能取值列表,然后明确每个格子所代表的实际含义,再进行概率计算即可

标准差等的均值,方差性质
样本均值就是分布均值,与取样数量N无关;样本方差为分布方差除以N。
样本均值的均值是分布均值。
样本方差
样本均值为X拔,样本均值的均值就是总体均值;
样本均值的方差是总体方差除以N
样本方差为S的平方,样本方差的均值等于总体的方差
区分样本均值的方差与样本方差
还需要区分的是,样本均值与样本,即X拔与X,X与μ,X拔与μ
另外,对于样本方差的方差,考虑构建卡方分布
即样本方差为N-1,除以总体方差后,可以转为N-1的卡方分布,然后样本方差的方差,可以转化为卡方分布的方差,卡方分布的方差为二倍的自由度

两种方法,一种是转为自由度为1的卡方分布,然后注意卡方分布的方差为2^N,均值为N;一种是利用方差的定义,即样本减去均值的差的均值,满足这个式子,所以就是在问样本方差,为原样本方差除以取样数量
还有一种思路是,涉及均值,绝对值等要素组合在一起时,考虑直接积分,利用正态分布的对称性进行求解。

ES^2=DX,E(X拔^2)=D(X拔)+E(X拔)^2,
D(X拔)=1/nDX,E(X拔)=EX

常见分布
正态分布公式背写,


常见分布缩写,P是泊松,E是指数,G是几何分布
常见分布的期望与方差,泊松的期望就是朗姆达,方差?
指数的期望是1/朗姆达,方差为1/朗姆达的平方。(理解为,指数分布的含义为等待时间,参数朗姆达的含义为发生次数,即频率,所以平均等待时间为频率事件间的间隔,1/朗姆达)
几何分布?在指数分布的基础上,就只是方差还要再多乘一个1-p,即1-参数
二项分布为期望为np,方差为np(1-p)

![]()
对于后一项的处理方式,为直接积分,即回归期望的定义。
对于期望式中难以处理的部分,如绝对值以及其他不能转换的部分,可以考虑直接通过期望定义来进行积分计算

第一空,就是直接离散化计算概率,不用考虑卷积公式。第二问就是直接展开,利用独立分布时,EXY=EXEY进行计算

此题需要注意,平均就诊时间是参数的倒数,参数的含义 是一定时间内事件发生的次数、频率,所以间隔时间是参数的倒数
密度:朗姆达E^-朗姆达,分布:1-E^-朗姆达

总点击次数为4,类似前题,直接离散化穷举计算即可
两个都服从泊松分布,第一个参数为3,第二个参数为2。用卷积公式,这两个是独立的,然后有一个联合密度函数,就在那个联合密度函数上进行卷积公式。也不用卷积公式,直接离散化的穷举计算即可

满足指数分布,可以直到各自的均值与方差,然后由相关系数知道均方差,均方差=EXY-EXEY,就求出EXY
指数分布的均值为参数的倒数,方差为参数倒数的平方,也是均值的平方
泊松分布的均值为参数,方差也为参数
几何分布的均值为参数的倒数,方差为参数倒数的平方基础上再乘个Q

基于标准正态分布间的转化
卡方分布是直接相加
T分布是分子为一个标准正态,卡方为分布除以其自由度后开根号 。T的自由度就是分母卡方的自由度
F分布分子分母均为卡方除以其自由度后开根号
样本方差除以方差可以转化为卡方分布
从而,样本方差在分子上时,可为卡方分布;在分母上是,为标准差的形式,则为除以自由度后开根号,即T分布。分子分母都有样本方差,考虑F分布
即出现样本方差,就需要考虑到卡方分布,T分布,F分布

X与Y独立,且都为标准正态分布,那么平方加和为自由度为2的卡方分布,找分位点即可
相同原理可以应用于炮弹落点为(X,Y),且X,Y独立满足标准正态分布,那么落地到原点的距离Z满足Z^2=X^2+Y^2,即Z^2服从自由度为2的卡方分布

第一空直接运算,就是自由度为6的卡方分布

DS^2,考虑构造卡方分布,(N-1)S^2/方差为自由度为N-1的卡方分布,然后卡方分布的方差为两倍的自由度,即可得;第二空,为自由度为N-1的T分布,T分布的均值为0,方差为N/N-2;第三空为自由度为1的卡方分布
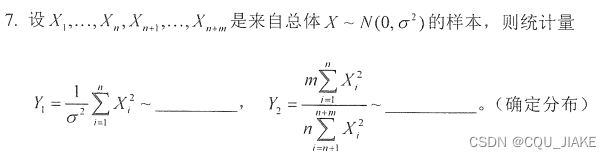
第一空为自由度为N的卡方分布;第二空为F分布,分子自由度为N,分母为M
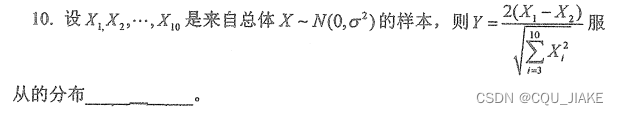
注意分母的i是从3开始1,而不是从1开始的,还有就是T分布与F分布一定要注意除以各自的自由度

注意第一个空,为样本均值,减完后,其分布满足均值为0,因为样本均值的均值等于总体均值
但要注意它的方差,样本均值不是一个常量,而是一个变量,如果为常量,如总体均值,那么这个分布的方差不会变;但是为样本均值,它的方差为总体方差除以n,但是依然不能直接运算,因为X1与样本均值不独立,应把其拆为独立的部分后再进行运算
对于第二问,涉及到样本均值,就一定会有样本方差,考虑自由度减1;不可用第一问的结论,因为这N个分布并不相互独立,而卡方分布必须满足相加的各几个分布相独立
统计量的性质
无偏估计
若为无偏估计,那么统计量的均值为数值期望

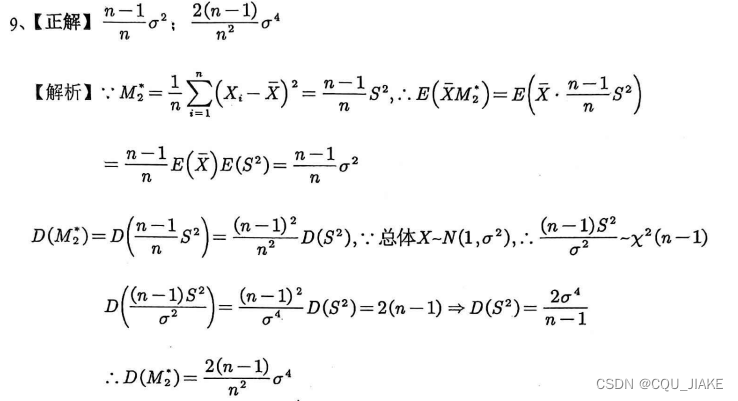


三个想法;第一是直接拆开,然后进行运算;第二是构建辅助分布,然后利用卡方分布;第三同样是辅助分布,但是是利用EX^2转方差的性质。
这里需要注意是可以成功构建一个卡方分布的,因为两两样本间的差值是相互独立的,但是需要注意上例中,涉及到样本均值就无法建立卡方分布,因为样本均值并非与每个样本独立。

置信区间的计算
对于总体均值的置信区间,若总体方差已知,就构建正态分布
若总体方差未知,就构建T分布
对于总体方差的置信区间,无论总体均值是否已知,都构建卡方分布来进行求解,
若总体均值已知,那么分子上的X-均值,就是一个一个算
若总体均值未知,那么分子上的X-均值,就不能一个一个算,因为此时总体均值不知道,那么就是通过样本方差来解决这一问题,即N-1乘以样本方差,等于那个,不过是自由度减一,而且每项减的是样本均值而不是总体均值
在总体方差估计区间中,需注意卡方分布是不对称的,也就是要查两次表,左右都是二分之α的水平

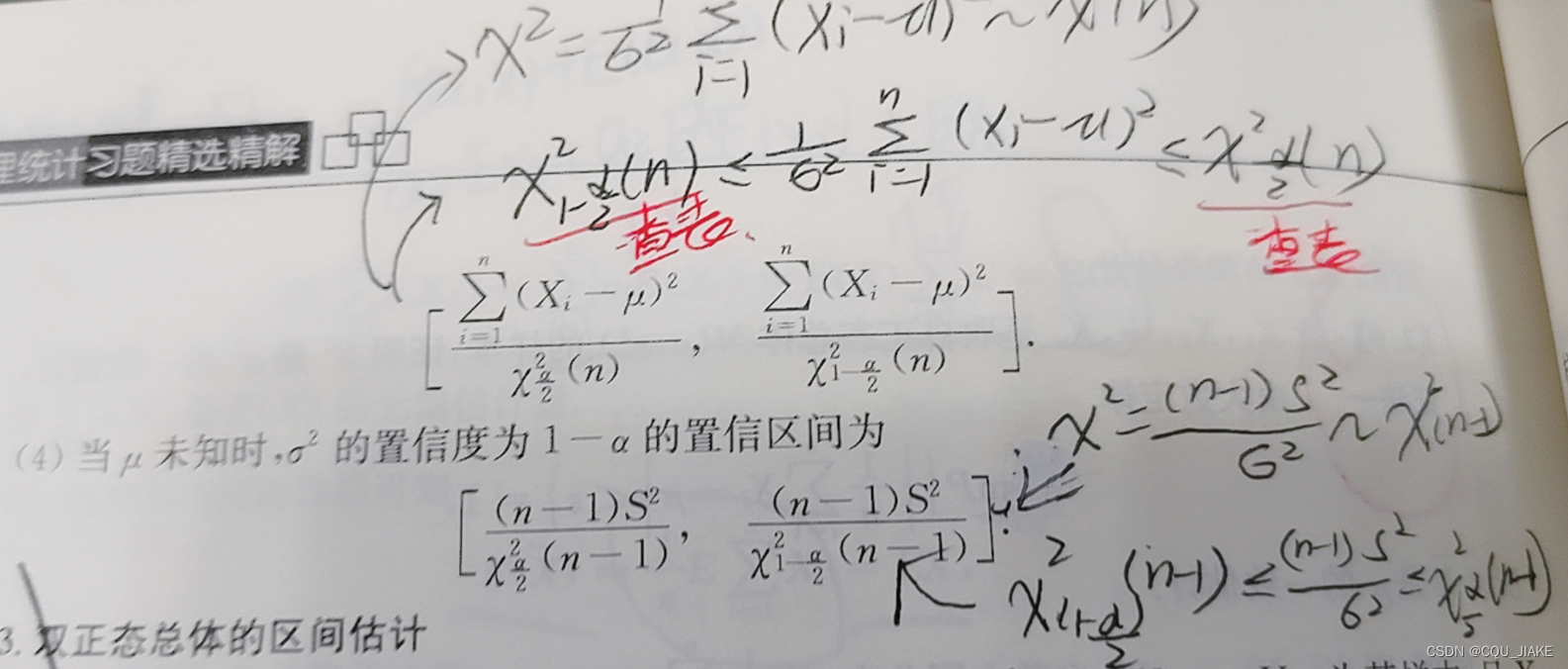

对总体方差估计,总体均值未知,采用N-1的卡方分布,问有无增大,所以检验假设为方差<=70,统计量应分布于左侧,拒绝域为右侧,右侧占0。05

对方差估计,均值未知,考虑自由度为N-1的卡方分布,即(N-1)样本方差除以估计方差,左右两侧为α/2的水平

对总体均值估计,方差已知,采用标准正态,注意假设为均值小于等于32,然后统计量水平为单侧(左侧),拒绝域在右侧

对总体均值的估计,总体方差不知,用自由度-1的T分布,左右为二分之α,即0.025

对总体均值估计,总体方差未知,采用自由度N-1的T分布,置信度95%,分布在左右两侧

对总体方差估计,总体均值未知,采用N-1的卡方分布,分子为N-1*S^2,分母为方差,左右为α/2






问方差,方差估计,那就是卡方分布,由于均值未知,所以依据样本方差构建,样本方差乘(样本数量-1)除以总体方差,就是n-1的卡方分布,问是否明显变化,双侧估计,拒绝域就是比1-α/2小或者比α/2大
第一类第二类错误
第一类第二类错误理解
主要是第二类错误的计算
第一类错误是说原假设为真,然后放弃原假设,即弃真错误;第二类错误是说原假设为假,接受原假设。一般思路为固定犯第一类错误的概率,然后缩小第二类错误的概率。
犯第一类错误的概率就是α,固定后,就可以确定拒绝域边界的情况。
犯第二类错误,原假设为假,依然接受,那么就是依据第一类错误固定下的边界C,可以表达出相应量在的一个区间里(即不在拒绝域内),然后可以计算在实际分布条件下分布在这个区间里的概率
就是说,拒绝域的边界值,和第一类错误的概率,α水平息息相关,互为决定。

变量间转换,概率计算题
求积分公式
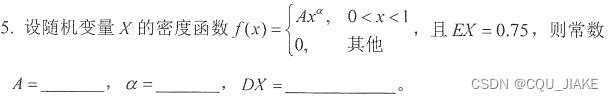
涉及一维与二维
考虑平方的转化
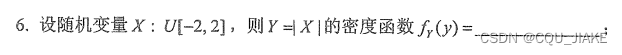

卷积公式计算



证明题

似然估计练练






理解
密度函数与分布函数的理解
有一个函数,它可以取很多值,如果取每个值的概率都一样,那就是分布均匀的,是均匀函数,如果分布不均匀,就不是均匀函数分布;每个值在函数取值出现的概率就是密度函数,均匀时都一样;不均匀时根据出现的值,有其对应的出现概率。
分布函数可以理解为,分布函数这个值,然后函数取值的点落在这个值划定的左区间内的概率(或者可以说是占比)
从这个角度,密度函数的自变量取值范围,就是对应会出现的值,然后这个值通过密度函数会得到其出现的概率;而分布函数就是立一个区间右端点,然后问自变量(可能出现的值)取值在这个区间里的概率。
二维变量密度函数,卷积公式理解
卷积公式就是,原来两个变量x,y,然后有一个z综合了2个变量的信息,通过卷积公式就是把其中一个变量视为常数,然后用z去替换掉剩下的那个变量,利用的方式就是一维的函数替换,求反函数,然后乘一个求导(注意另一个变量在此时表现为常数),之后就得到了把其中一个变量替换后的x,z联合分布(以替换y为例),然后再对每个z收缩其所有的x,即可求得z的单独密度函数。
即替掉哪个变量(计为Y)时,就求Y与Z的关系式(Y为因变量),把X视为常数,然后在函数里踢掉Y为Z,然后乘一个YZ关系式中对Z求导的结果(可能涉及到X,求导时其视为常数),最后就收缩所有的X得到Z的式子。
第一步是要得到联合密度函数,就是把不同变量X,Y的取值综合在一起的一个密度联式
在一维当中,Y与X满足一个关系式(Y为因变量),X已知分布函数,那么转换求反函数,得到X为因变量的与Y的关系式,然后这个表达式对Y求导,取绝对值,把X当中的换掉为Y,就是Y的分布函数
对于泊松分布与指数分布的区分
泊松分布与指数分布共用一个参数,就是朗姆达,这个参数的含义就是一定时间内事件发生的次数,频率,是次数、频率。
相应的,等待时间,寿命,就是频率的倒数。
要根据实际意义确定真正的朗姆达
相关文章:

12.4~12.14概率论复习与相应理解(学习、复习、备考概率论,这一篇就够了)
未分配的题目 概率计算(一些转换公式与全概率公式)与实际概率 ,贝叶斯 一些转换公式 相关性质计算 常规,公式的COV与P 复习相关公式 计算出新表达式的均值,方差,再套正态分布的公式 COV的运算性质 如…...

关于多重背包的笔记
多重背包可以看作01背包的拓展, 01背包是选或者不选。多重背包是选0个一直到选s个。 for (int i 1; i < n; i) {for (int j m; j > w[i]; --j){f[j] max(f[j], f[j - 1*w[i]] 1*v[i], f[j - 2*w[i]] 2*v[i],...f[j - s*w[i]] s*v[i]);} } 由上述伪代码…...

如何使用 Java 的反射
如何使用 Java 的反射? 通过一个全限类名创建一个对象 Class.forName(“全限类名”); 例如:com.mysql.jdbc.Driver Driver 类已经被加载到 jvm 中,并且完成了类的初始化工作就行了 类名.class; 获取 Class<?> clz 对象对…...
PLC-Recorder V3 修改服务器和客户端通讯端口的方法
PLC-Recorder V3是服务器和客户端的架构,他们之间用TCP通讯。如果客户端无法与服务器建立连接(重启也无效,并且确保没有老版本的PLC-Recorder在运行),则可能是端口被占用了。这时候需要修改他们之间的通讯端口…...
libevent服务GET/POST的简单使用
目录 1、前言2、测试demo2.1、目录结构2.2、 测试源码2.2.1、http_server.cpp2.2.2、 http_server.h 2.3、 编译2.4、 运行结果2.4.1、测试POST2.4.2 、测试GET请求 1、前言 项目开发中经常需要使用到私有协议和Qt,Android等GUI前端通信,比较常用的使用POST和GET方式…...
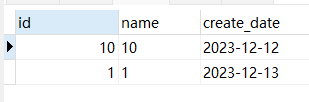
MySQL 系列:注意 ORDER 和 LIMIT 联合使用的陷阱
文章目录 前言背后的原因ORDER BY 排序列存在相同值时返回顺序是不固定的LIMIT 和 ORDER BY 联合使用时的行为ORDER BY 或 GROUP BY 和 LIMIT 联合使用优化器默认使用有序索引 如何解决其它说明个人简介 前言 不知道大家在在分页查询中有没有遇到过这个问题,分页查…...

通过实例理解OAuth2授权
在之前的《通过实例理解Go Web身份认证的几种方式[1]》和《通过实例理解Web应用授权的几种方式[2]》两篇文章中,我们对Web应用身份认证(AuthN)和授权(AuthZ)的几种方式做了介绍并配以实例增强理解。 在现实世界中,还有一大类的认证与授权是在前面的文章中…...
MATLAB2022安装下载教程
安装包需从夸克网盘自取: 链接:https://pan.quark.cn/s/373ffc9213a1 提取码:N7PW 1.将安装包解压 2.以管理员的身份运行文件夹中的setup文件 3.点击高级选项--->我有文件安装密钥 4. 选择【是】,进入下一步 5.输入密钥 0532…...

从零开始搭建Go语言开发环境
https://www.liwenzhou.com/posts/Go/install_go_dev/ “go 命令现在默认在模块感知模式下构建包,即使没有 go.mod 存在也是如此。 “您可以将 GO111MODULE 设置为 auto,仅当当前目录或任何父目录中存在 go.mod 文件时,才能启用模块感知模式…...
vite+vue3+ts+tsx+ant-design-vue项目框架搭建
参与公司项目开发一段时间了,项目用到了很多新的技术(vite,vue3,ts等等),但是框架都是别人搭好的,然后就想说如果是自己的话,会从零搭建一个吗,于是就有了这篇文章。 目录 一、涉及到的相关依…...

【5G PHY】5G小区类型、小区组和小区节点的概念介绍
博主未授权任何人或组织机构转载博主任何原创文章,感谢各位对原创的支持! 博主链接 本人就职于国际知名终端厂商,负责modem芯片研发。 在5G早期负责终端数据业务层、核心网相关的开发工作,目前牵头6G算力网络技术标准研究。 博客…...
创建个人网站(一)从零开始配置环境,搭建项目
目录 前言配置环境前端后端遇到的问题1.安装了nvm和node,vscode没反应2.安装完脚手架之后vue指令不存在 vscode插件(以后遇到好的会添进去) 前言 从刚开始学前端的html直到现在前后端都有在开发,我一直都有一个想法,就…...

fripside - promise lrc
[ti:promise] [ed:2] [rt:20] [ml:0|0] [00:05.172]words:Satoshi Yaginuma, Shinichiro Yamashita [00:09.664]music&arrangement:Satoshi Yaginuma, Shigetoshi Yamada [00:14.565]PCゲーム「ENGAGE LINKS」 (Alcot) エンディングテーマ [00:20.000] [00:46.442]朝の陽射…...

网络连接和协议
网络连接是通过一系列协议来实现的,其中TCP/IP协议和HTTP协议是其中两个关键的协议。 1. **TCP/IP协议:** - TCP/IP(Transmission Control Protocol/Internet Protocol)是一组用于在互联网上传输数据的协议。它是一个层次化的…...
MySQL数据库,表的增量备份与恢复
1. 从物理与逻辑的角度 数据库备份可以分为物理备份和逻辑备份。物理备份是对数据库操作系统的物理文件(如数据 文件,日志文件等)的备份。这种类型的备份适用于在出现问题时需要快速恢复的大型重要数据库。 物理备份又可以分为冷备份…...
13.Spring 整合 Kafka + 发送系统通知 + 显示系统通知
目录 1.Spring 整合 Kafka 2.发送系统通知 2.1 封装事件对象 2.2 开发事件的生产者和消费者 2.3 触发事件:在评论、点赞、关注后通知编辑 3.显示系统通知 3.1 通知列表 3.1.1 数据访问层 3.1.2 业务层 3.1.3 表现层 3.2 开发通知详情 3.2.1 开发数据…...
windows 服务器 怎么部署python 程序
一、要在 Windows 服务器上部署 Python 程序,您需要遵循以下步骤: 安装 Python:首先,在 Windows 服务器上安装 Python。您可以从官方网站(https://www.python.org/downloads/windows/)下载最新的 Python 安…...

Chapter 7 - 2. Congestion Management in Ethernet Storage Networks以太网存储网络的拥塞管理
Location of Ingress No-Drop Queues入口无损队列的位置 Ingress queues for no-drop traffic are maintained by all the ports in a lossless Ethernet network. For the sake of simplicity, Figure 7-1 shows ingress no-drop queue(s) only at one location, but in real…...

深入理解前端项目中的 package.json
在前端开发中,package.json 是一个很重要的文件,它在Node.js和前端项目中扮演着重要的角色。这个文件用于存储项目的元数据以及管理项目的依赖关系。 package.json 文件是每个Node.js项目和许多前端项目的核心。它不仅定义了项目的基本属性,…...

4-Docker命令之docker build
1.docker build介绍 docker build命令是用来使用Dockerfile文件创建镜像 2.docker build用法 docker build [参数] PATH | URL | - [root@centos79 ~]# docker build --helpUsage: docker buildx build [OPTIONS] PATH | URL | -Start a buildAliases:docker buildx build…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...

