<蓝桥杯软件赛>零基础备赛20周--第10周--二分
报名明年4月蓝桥杯软件赛的同学们,如果你是大一零基础,目前懵懂中,不知该怎么办,可以看看本博客系列:备赛20周合集
20周的完整安排请点击:20周计划
每周发1个博客,共20周(读者可以按自己的进度选“正常”和“快进”两种计划)。
每周3次集中答疑,周三、周五、周日晚上,在QQ群上答疑:

文章目录
- 1. 二分基础
- 1.1 二分概念
- 1.2 基本代码
- 1.3 二分的应用条件
- 1.4 中值mid的计算方法
- 2. 经典应用:最小值最大化、最大值最小化
- 3. 例题
- 3.1 简单二分:求阶乘
- 3.2 简单二分:分巧克力
- 3.3 最小值最大化:跳石头
- 3.4 简单题:青蛙过河
- 3.5 中等题:技能升级
第9周: 二分
备赛20周活动已经到第10周了,也快到期末考试阶段了。大家先准备考试,有空做做竞赛题。
1. 二分基础
二分是蓝桥杯省赛的必考知识点,每年都有。本文的例题大多都是蓝桥杯省赛真题。
(本博主曾写过一篇 二分法、三分法,非常详细地介绍了二分法的原理和例题,请参考。今天这篇博客,介绍了二分的基础内容,以及在蓝桥杯中的应用。)
1.1 二分概念
“二分法”是一种思路简单、编码容易、效率极高、应用广泛的算法。在任何算法竞赛中,二分法都是最常见的知识点之一。
二分法的思想很简单,每次把搜索范围缩小一倍,直到找到答案为止。
设初始范围是[L, R],常见的二分法代码这样写:
while (L < R){ //一直二分,直到区间[L,R]缩小到L=Rint mid = (L + R) / 2; //mid是L、R的中间值if (check(mid)) R = mid; //答案在左半部分[L,mid],更新R=midelse L = mid + 1; //答案在右半部分[mid+1, R],更新L=mid+1
}
答案在区间[L, R]中,通过中间值mid缩小搜索范围。这样搜索答案:
(1)如果答案在左半部分,把范围缩小到[L, mid],更新R=mid,然后继续。
(2)如果答案在右半部分,把范围缩小到[mid+1, R],更新L=mid+1,然后继续。
经过多次二分,最后范围缩小到L=R,这就是答案。
二分的效率极高,例如在 10 亿 = 2 30 10亿=2^{30} 10亿=230个数字中查找某个数,前提是这些数已经排序,然后用二分法来找,最多只需找30次。把二分法的计算复杂度记为O(logn)。
以猜数字游戏为例,一个[1, 100]内的数字,猜7次就能猜出来。例如猜数字68:
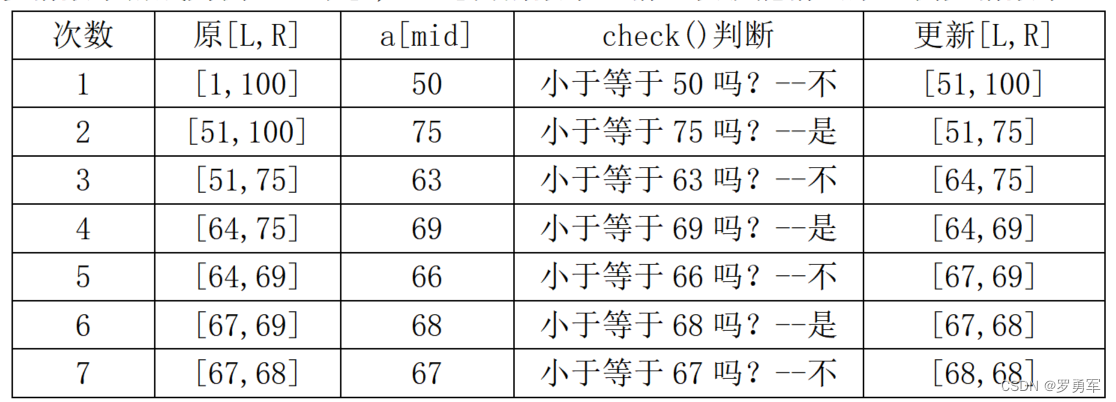
1.2 基本代码
下面是“猜数游戏”的C++代码实现。二分函数bin_search()操作3个变量:区间左端点L、右端点R、二分的中位数mid。每次把区间缩小一半,把L或R更新为mid;直到L= R为止,即找到了答案所处的位置。
#include<bits/stdc++.h>
using namespace std;
int a[105];
bool check(int x,int mid){ //二分中的检查函数return x <= a[mid]; //如果x小于等于中间数,返回true
}
int bin_search(int n, int x){ //在数组a中找数字x,返回位置int L = 1, R = n; //初始范围[L, R]while (L < R) {int mid = (L+R)/2;if (check(x,mid)) R = mid; //答案在左半部分:[L,mid]else L = mid+1; //答案在右半部分:[mid+1, R]}return a[L]; //返回答案
}
int main(){int n = 100;for(int i=1;i<=n;i++) a[i]=i; //赋值,数字1~100int x = 68; //猜68这个数cout<<"x="<<bin_search(n,x);
}
Java代码
import java.util.*;
class Main {static int[] a = new int[105];static boolean check(int x, int mid) { return x <= a[mid]; }static int bin_search(int n, int x) {int L = 1;int R = n;while (L < R) {int mid = (L + R) / 2;if (check(x, mid)) R = mid;else L = mid + 1; }return a[L];}public static void main(String[] args) {int n = 100;for (int i = 1; i <= n; i++) a[i] = i; int x = 68;System.out.println("x=" + bin_search(n, x));}
}
Python代码
def check(x, mid): return x <= a[mid]
def bin_search(n, x):L, R = 1, nwhile L < R:mid = (L+R) // 2if check(x, mid): R = midelse: L = mid + 1return a[L]n = 100
a = [0] * 105
for i in range(1, n + 1): a[i] = i
x = 68
print("x=", bin_search(n, x))
1.3 二分的应用条件
二分法把长度为n的有序序列上O(n)的查找时间,优化到了O(logn)。
注意二分法的应用条件是:序列是单调有序的,从小到大,或从大到小。在无序的序列上无法二分,如果是乱序的,应该先排序再二分。
如果在乱序序列上只搜一次,不需要用二分法。如果用二分,需要先排序,排序复杂度O(nlogn),再二分是O(logn),排序加二分的总复杂度O(nlogn)。如果用暴力法直接在乱序的n个数里面找,复杂度是O(n)的,比排序加二分快。
但是如果不是搜一个数,而是搜m个数。那么先排序再做m次二分的计算复杂度是O(nlogn+mlogn),而暴力法是O(mn)的,当m很大时,二分法远好于暴力法。
做二分法题目时,需要建模出一个有序的序列,并且答案在这个序列中。编程时,根据题目要求确定区间[L, R]范围,并写一个check()函数来更新L和R。
1.4 中值mid的计算方法
[L, R]的中间值mid,有多种计算方法:
mid = (L+R)/2
mid = (L+R)>>1
mid = L+(R-L)/2
下表(《算法竞赛》清华大学出版社45页)对比了它们的优缺点。一般情况下,用哪个都行。

2. 经典应用:最小值最大化、最大值最小化
二分法的经典应用场景是“最小值最大化(最小值尽量大)”、“最大值最小化(最大值尽量小)”。
(1)最小值最大化
有n个牛棚,分布在一条直线上,有k头牛,给每头牛安排一个牛棚住,k<n。由于牛脾气很大,所以希望让牛之间尽量住得远一些。这个问题简化为:在一条直线上有n个点,选k个点,其中某两点之间的距离是所有距离中最小的,求解目标是让这个最小距离尽量大。这就是“最小值(两点间的最小距离)最大化”。
“牛棚问题”的求解可以用猜的方法。猜最小距离是D,看能不能在n个点中选k个,使得任意两点之间的距离≥D。如果可以,说明D是一个合法的距离。然后猜新的D,直到找到那个最大的合法的D。
具体操作是:从第1个点出发,然后逐个检查后面的点,第一个距离≥D的点,就是选中的第2点;然后从第2点出发,再选后面第一个距离第2点≥D的点,这是选中的第3点;…继续下去,直到检查完n个点。这一轮猜测的计算复杂度是O(n)的。
检查完n个点,如果选中的点的数量≥k,说明D猜小了,下次猜大点;如果选中的点的数量<k,说明D猜大了,下次猜小点。
如何猜D?简单的办法是从小到大一个个试,但是计算量太大了。
用二分法可以加速猜D的过程。设D的初值是一个极大的数,例如就是所有n点的总长度L。接下来的二分操作和前面的“猜数字游戏”一样,经过O(logL)次,就能确定D。
总计算量:一共O(logL)轮猜测,每一轮O(n),总计算量为O(nlogL)。
(2)最大值最小化
经典的例子是“序列划分”问题。有一个包含n个正整数的序列,把它划分成k个子序列,每个子序列是原数列的一个连续部分,第i个子序列的和为Si。在所有s中,有一个最大值。问如何划分,才能使最大的s最小?这就是“最大值(所有子序列和的最大值)最小化”。
例如序列{2, 2, 3, 4, 5, 1},将其划分成k=3个连续的子序列。下面举例2种分法:{(2, 2, 3)、(4, 5)、(1)},子序列和分别是7、9、1,最大值是9;{(2, 2, 3)、(4)、(5,1)},子序列和是7、4、6,最大值是7。第2种分法比第1种好。
仍然用猜的方法。在一次划分中猜一个x,对任意的Si都有Si ≤ x,也就是说,x是所有Si中的最大值。
如何找到这个x?简单的办法是枚举每一个x,用贪心法每次从左向右尽量多划分元素,Si不能超过x,划分的子序列个数为k个。但是枚举所有的x太耗时了。
用二分法可以加速猜x的过程。用二分法在[max, sum]范围内查找满足条件的x,其中max是序列中最大元素的值,sum是所有元素的和。
3. 例题
3.1 简单二分:求阶乘
蓝桥杯2022初赛题:求阶乘
链接1
链接2
题解:
尾零是2×5相乘得到的,所以只需要计算n!中2和5的因子的数量。又因为n!中2的因子数量远大于5的因子数量,所以只需要计算5的因子数量。
例如25!=25×…×20×…×15×…×10×…×5×…,其中的25、20、15、10、5分别有2、1、1、1、1共6个因子5,所以尾零有6个。
(1)通过30%测试。
简单的方法是检查每个n,计算n!的尾零数量,尾零数量等于k的n就是答案。下面代码第11行的for循环n/5次,对于100%的数据, 1 ≤ K ≤ 1 0 18 1≤K≤10^{18} 1≤K≤1018,由于n比k还大,代码超时。
函数check(n)返回n!的尾零数量,也就是计算n!有多少个因子5,读者可以按自己的思路实现这个函数。下面的check()用了巧妙的方法。以25!为例,对5有贡献的是5、10、15、20、25,即5×1、5×2、5×3、5×4、5×5,共有6个5,其中5个5是25/5得到的,即5×i中的5;还有一个5是循环5次后多了一个5,即i×5的5。再例如100!,尾零的数量包括两部分:100/5=20、20/5=4。
#include <bits/stdc++.h>
using namespace std;
#define ll long long
ll check(ll n) { //计算n!末尾有多少个0ll cnt = 0;while (n) cnt += (n /= 5); return cnt;
}
int main(){ll k; cin >> k;for(ll n=5;;n+=5){ //n是5的倍数,它含有因子5ll cnt = check(n); //cnt是n!的尾零数量if(cnt==k){ cout << n; break;}if(cnt>k) { cout <<-1; break;}}return 0;
}
(2)通过100%测试。
本题容易想到可以用二分优化,也就是用二分来猜n。因为n递增时,尾零的数量也是单调递增的,符合二分法的应用条件。
下面讨论代码的计算复杂度。第12行的二分是 O ( l o g E ) O(logE) O(logE),这里 E = 1 0 19 E=10^{19} E=1019。第4行做一次check()差不多是O(1)的。总计算量约为 l o g E = l o g 1 0 19 logE = log10^{19} logE=log1019 < 70次。
C++代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long
ll check(ll n) { //计算n!末尾有多少个0ll cnt = 0;while (n) cnt += (n /= 5);return cnt;
}
int main() {ll k; cin >> k;ll L = 0, R = 1e19; //R的初值为一个极大的数while (L < R) {ll mid = (L + R) >> 1;if (check(mid) >= k) R = mid; // mid!的尾零数量超过了k,说明mid大了else L = mid + 1; // mid小了}if (check(R) == k) cout << R ;else cout << -1;return 0;
}
java代码
import java.util.Scanner;
public class Main {public static long check(long n) {long cnt = 0;while (n > 0) {cnt += n / 5;n /= 5;}return cnt;}public static void main(String[] args) {Scanner scanner = new Scanner(System.in);long k = scanner.nextLong();long L = 0;long R = (long) Math.pow(10, 19);while (L < R) {long mid = (L + R) / 2;if (check(mid) >= k) R = mid;else L = mid + 1;}if (check(R) == k) System.out.println(R);else System.out.println(-1);}
}
python代码
def check(n):cnt = 0while n:cnt += n // 5n //= 5return cnt
k = int(input())
L = 0
R = 10**19
while L < R:mid = (L + R) // 2if check(mid) >= k: R = midelse: L = mid + 1
if check(R) == k: print(R)
else: print(-1)
3.2 简单二分:分巧克力
分巧克力: 2017年第八届蓝桥杯省赛
链接1
链接2
题解:
(1)通过50%的测试。
先试试暴力法:把边长从1开始到最大边长d,每个值都试一遍,一直试到刚好够分的最大边长为止。编码:边长初始值d = 1,然后d = 2, 3, 4, …一个个试。
#include<bits/stdc++.h>
using namespace std;
int h[100010],w[100010];
int n,k;
bool check(int d){ //检查够不够分int num=0;for(int i=0;i<n;i++) num += (h[i]/d)*(w[i]/d);if(num>=k) return true; //够分else return false; //不够分
}
int main(){cin >>n>>k;for(int i=0;i<n;i++) cin>>h[i]>>w[i];int d=1; //正方形边长while(1){if(check(d)) d++; //边长从1开始,一个个地暴力试else break;}cout << d-1;return 0;
}
暴力法的复杂度:n个长方形,长方形的最大边长d。第16行check()一次的计算量是O(n),需要做d次check(),总复杂度O(n×d),而n和d的最大值是 1 0 5 10^5 105,超时。
(2)通过100%测试
一个个试边长d太慢了,现在使用二分,按前面的“猜数游戏”的方法猜d的取值。暴力法需要做d次check(),现在用二分法,只需要做O(logd)次check()。具体操作是:
第一次:开始时d的范围是1~D,试试中间值D/2,如果这个值大了,就把范围缩小为0 ~ D/2,如果这个值小了,就把范围缩小为D/2 ~ D;
第二次,取新的中间值D/4或3D/4,再试…
…
直到找到合适的值为止。
C++代码
整数的二分法的编码虽然简单,但是很容易出错。左右边界L、R和中间值mid的迭代,由于整数的取整问题,极易出错,导致死循环。下面的代码给出了两种写法,有细微而关键的区别,请仔细领会并彻底理解这两种写法。
#include<bits/stdc++.h>
using namespace std;
int n,k;
const int N=100010;
int h[N],w[N];
bool check(int d){int num=0;for(int i=0;i<n;i++) num += (h[i]/d)*(w[i]/d);if(num>=k) return true; //够分else return false; //不够分
}
int main(){cin >> n >> k;for(int i=0;i<n;i++) cin>>h[i]>>w[i];int L=1, R=N; //D的初值是R=100010
//第一种写法:while(L<R) {int mid=(L+R+1)>>1; //除2,向右取整if(check(mid)) L=mid; //新的搜索区间是右半部分,R不变,调整L=midelse R=mid-1; //新的搜索区间是左半部分,L不变,调整R=mid–1}cout << L;
//第二种写法:
/* while(L<R) {int mid=(L+R)>>1; //除2,向左取整if(check(mid)) L=mid+1; //新的搜索区间是右半部分,R不变,更新L=mid+1else R=mid; //新的搜索区间是左半部分,L不变,更新R=mid}cout << L-1; */return 0;
}
java代码
import java.util.Scanner;public class Main {static int n, k;static final int N = 100010;static int[] h = new int[N];static int[] w = new int[N];static boolean check(int d) {int num = 0;for (int i = 0; i < n; i++)num += (h[i] / d) * (w[i] / d);if (num >= k) return true; // 够分else return false; // 不够分}public static void main(String[] args) {Scanner scanner = new Scanner(System.in);n = scanner.nextInt();k = scanner.nextInt();for (int i = 0; i < n; i++) {h[i] = scanner.nextInt();w[i] = scanner.nextInt();}int L = 1, R = N; // D的初值是R=100010while (L < R) {int mid = (L + R + 1) >> 1; // 除2,向右取整if (check(mid)) L = mid; // 新的搜索区间是右半部分,R不变,调整L=midelse R = mid - 1; // 新的搜索区间是左半部分,L不变,调整R=mid–1}System.out.println(L);scanner.close();}
}
python代码
def check(d):global w,hnum = 0for i in range(len(w)):num += (w[i]//d) * (h[i]//d)if num >= k: return Truereturn False
n,k = map(int,input().split())
w = []
h = []
for i in range(n):a,b = map(int,input().split())w.append(a)h.append(b)
L ,R = 1, 100010
while L < R:mid = (L+R)//2if check(mid): L = mid +1else : R = mid
print(L-1)
3.3 最小值最大化:跳石头
跳石头:链接
这是一道二分法应用的套路题:“最小值最大化”。
在n块岩石中移走m个石头,有很多种移动方法。在第i种移动方法中,剩下的石头之间的距离,有一个最小距离ai。在所有移动方法的最小距离ai中,问最大的ai是多少。
在所有可能的最小值中,找最大的那个,就是“最小值最大化”。
如果用暴力法找所有的组合,在n块岩石中选m个石头有n!/m!(n-m)!种组合,情况太多,显然会超时。
可以转换思路,不去找搬走石头的各种组合,而是给出一个距离d,检查能不能搬走m块石头而得到最短距离d。把所有的d都试一遍,肯定能找到一个最短的d。用二分法找这个d即可。
C++代码
下面的代码中,17 ~ 21行用二分法找一个最小距离d。函数check(d)函数检查d这个距离是否合适。
请保证自己能写出代码,确保能完全写出整数二分而不出错。
#include<cstdio>
int len,n,m;
int stone[50005];
bool check(int d){ //检查距离d是否合适int num=0; //num记录搬走石头的数量int pos=0; //当前站立的石头for(int i=1;i<=n;++i)if(stone[i]-pos < d) num++; //第i块石头可以搬走else pos = stone[i]; //第i块石头不能搬走if(num <= m) return true; //要移动的石头比m少,满足条件else return false; //要移动的石头比m多,不满足条件
}
int main(){scanf("%d%d%d",&len,&n,&m);for(int i=1;i<=n;++i) scanf("%d",&stone[i]);int L=0,R=len,mid;while(L<R){mid = L+(R-L)/2;if(check(mid)) L = mid+1; //满足条件,说明mid小了,调大一点else R = mid-1; //不满足条件,说明mid大了,调小一点}if(!check(L)) L -= 1;printf("%d\n",L);return 0;
}
java代码
import java.util.Scanner;public class Main {static int len, n, m;static int[] stone;static boolean check(int d) {int num = 0; // num记录搬走石头的数量int pos = 0; // 当前站立的石头for (int i = 1; i <= n; ++i)if (stone[i] - pos < d) num++; // 第i块石头可以搬走else pos = stone[i]; // 第i块石头不能搬走if (num <= m) return true; // 要移动的石头比m少,满足条件else return false; // 要移动的石头比m多,不满足条件}public static void main(String[] args) {Scanner scanner = new Scanner(System.in);len = scanner.nextInt();n = scanner.nextInt();m = scanner.nextInt();stone = new int[n + 1];for (int i = 1; i <= n; ++i) stone[i] = scanner.nextInt();int L = 0, R = len, mid;while (L < R) {mid = L + (R - L) / 2;if (check(mid)) L = mid + 1; // 满足条件,说明mid小了,调大一点else R = mid - 1; // 不满足条件,说明mid大了,调小一点}if (!check(L)) L -= 1;System.out.println(L);scanner.close();}
}
python代码
len, n, m = map(int, input().split())
stone = [] # 石头i和到起起点的距离
def check(d):num = 0pos = 0 for i in range(0,n): # 0到n-1作为石头下标 if (stone[i]-pos < d): # 第i块可以搬走num += 1 else: pos = stone[i]if num <= m: return Trueelse: return False
for i in range(n):t = int(input())stone.append(t)
L, R = 0, len
while (L<R):mid = L+(R-L)//2if check(mid): L = mid+1else: R = mid-1
if check(L): print(L)
else: print(L-1)
3.4 简单题:青蛙过河
青蛙过河:2022年第十三届蓝桥杯省赛
链接1 链接2
题解:往返累计2x次相当于单向走2x次。跳跃能力越大,越能保证可以通过2x次。用二分法找到一个最小的满足条件的跳跃能力。设跳跃能力为mid,每次能跳多远就跳多远,用二分法检查mid是否合法。
C++代码
#include<bits/stdc++.h>
using namespace std;
int h[1000005];
int n,x;
bool check(int mid){long long sum=0;for(int i=0;i<mid-1;i++) sum+=h[i]; //mid-1个for(int i=0, j=mid-1;j<n;i++,j++) { //青蛙位置i,目标位置jsum += h[j];if(sum < 2*x) return false;sum -= h[i];}return true;
}
int main(){cin>>n>>x;for(int i=1;i<n;i++) cin>>h[i];int left=0, right=n;while(left<right){int mid=(left+right)/2;if(check(mid)) right = mid;else left = mid+1;}cout<<right;return 0;
}
java代码
import java.io.*;public class Main {static StreamTokenizer reader = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));static PrintWriter writer = new PrintWriter(new BufferedWriter(new OutputStreamWriter(System.out)));static int readInt() throws Exception {reader.nextToken();return (int)reader.nval;}static int N = 1000010;static int[] sum = new int[N];static int n, x;static boolean check(int len) {for(int i = 1; i + len <= n; i ++) {if(sum[i + len - 1] - sum[i - 1] < x) return false;}return true;}public static void main(String[] args) throws Exception {n = readInt(); x = readInt();x *= 2;for(int i = 1; i < n; i ++) {int t = readInt();sum[i] = sum[i - 1] + t;}int l = 1, r = n;while(l < r) {int mid = l + r >> 1;if(check(mid)) r = mid;else l = mid + 1;}writer.println(l);writer.flush();}
}
python代码
def check(mid):for i in range(mid, n):if sum[i] - sum[i-mid] < 2 * x: return Falsereturn True n, x = map(int, input().split())
h = list(map(int, input().split()))
sum = [0, h[0]]
for i in range(1, len(h)):sum.append(h[i] + sum[i])
L = 0
R = 100000
while L <= R:mid = (L + R) // 2if check(mid): R = mid - 1else: L = mid + 1
print(L)
3.5 中等题:技能升级
技能升级:2022年第十三届省赛
链接1
链接2
下面详细讲解多种方法,它们分别能通过40%、60%、100%的测试。
(1)暴力法:通过40%测试
先试试暴力法,直接模拟题意,升级m次,每次升级时选用最高攻击力的技能,然后更新它的攻击力。
下面用Python写代码。复杂度是多少?第12行升级m次,是O(m)的;第13行选用最大攻击,使用了Python的max()函数,是O(n)的。总复杂度O(mn),只能通过40%的测试。
import math
n,m = map(int,input().split())
a = [] # 存ai
b = [] # 存bi
c = [] # ai/bi
for i in range(n):a_,b_ = map(int,input().split())a.append(a_)b.append(b_) c.append(math.ceil(a_/b_)) #向上取整
ans = 0
for i in range(m): #一共升级m次max_num = max(a) #每次升级时,使用最大的攻击index = a.index(max_num ) #最大攻击对应的序号 a[index] -= b[index] #更新攻击力if c[index]>0: ans += max_num #累加攻击力c[index] -= 1
print(ans)
(2)暴力法+优先队列:通过60%测试
上面的代码可以稍做改进。在n个技能中选用最高攻击力,可以使用优先队列,一次操作的复杂度为O(logn)。m次升级,总复杂度O(mlogn),能通过60%的测试。
下面用C++的优先队列priority_queue实现。priority_queue默认是大根堆,用top()读取队列中的最大值。
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
typedef pair<int, int> PII;
priority_queue<PII> q; //默认是大根堆
PII p;
int main() {int n, m; cin >> n >> m;for (int i = 0; i < n; i++) {int a, b; cin >> a >> b;q.push(make_pair(a, b));}long long ans = 0;while (m--) { //升级m次if (q.empty()) break;p = q.top(); q.pop(); //每次升级时,使用最大的攻击。读队列最大值并删除ans += p.first; //累加攻击力p.first -= p.second; //更新攻击力if (p.first > 0) q.push(p); //重新放进队列}cout << ans;return 0;
}
java代码
import java.util.PriorityQueue;
import java.util.Scanner;public class Main {public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();int m = scanner.nextInt();PriorityQueue<PII> q = new PriorityQueue<>((a, b) -> b.first - a.first);for (int i = 0; i < n; i++) {int a = scanner.nextInt();int b = scanner.nextInt();q.add(new PII(a, b));}long ans = 0;while (m > 0 && !q.isEmpty()) {PII p = q.poll();ans += p.first;p.first -= p.second;if (p.first > 0) q.add(p);m--;}System.out.println(ans);}static class PII {int first;int second;PII(int first, int second) {this.first = first;this.second = second;}}
}
python代码
Python的“暴力法+优先队列”实现。优先队列用堆实现,heapq默认是小根堆,第7行把a取负,把最大值变成了最小值。
from heapq import *
n,m = map(int,input().split())
q = []
ans = 0
for i in range(n):a,b = map(int,input().split())heappush(q,(-a,b))
for i in range(m):p = heappop(q)a,b = -p[0],p[1]ans += aa = max(a - b, 0)if a != 0: heappush(q,(-a,b))
print(ans)
(3)二分法:通过100%测试
本题的正解是二分法,能通过100%的测试。
本题 m ≤ 2 × 1 0 9 m≤2×10^9 m≤2×109太大,若逐一升级m次必定会超时。但是不能直接对m进行二分,因为需要知道每个技能升级多少次,而这与m无关。
思考升级技能的过程,是每次找攻击力最高的技能。对某个技能,最后一次升级的攻击力,肯定比之前升级的攻击力小,也就是前面的升级都更大。可以设最后一次升级提升的攻击力是mid,对每个技能,若它最后一次能升级mid,那么它前面的升级都更大。所有这样最后能达到mid的技能,它们前面的升级都应该使用。用二分法找到这个mid,另外,升级技能减少的攻击力的过程是一个等差数列,用O(1)次计算即可知道每个技能升级了几次。知道了每个技能升级的次数,就可以计算一共提升了多少攻击力,这就是题目的答案
下面给出Python代码。函数check(mid)找这个mid。第6行,若所有技能升级总次数大于等于m次,说明mid设小了,在19行让L增大,即增加了mid。第7行,若所有技能升级总次数小于m次,说明mid设大了,在20行让R减小,即缩小了mid。
分析代码的复杂度。17~20行,二分 O ( l o g A ) O(logA) O(logA)次,这里A表示 1 ≤ A i ≤ 1 0 6 1≤Ai≤10^6 1≤Ai≤106;每次check()是O(n),二分的总复杂度是O(nlogA)。23行O(n)。代码的总复杂度是O(nlogA) + O(n),通过100%的测试。
c++代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll a[100005],b[100005];
int n, m;bool check(ll mid) {ll cnt = 0;for (int i = 0; i < n; i++) {if (a[i] < mid) continue;cnt += (a[i] - mid) / b[i] + 1;if (cnt >= m) return true;}return false;
}int main() {cin >> n >> m;for (int i = 0; i < n; i++) cin >> a[i] >> b[i];ll L = 1, R = 1000000;while (L <= R) {ll mid = (L + R) / 2;if (check(mid)) L = mid + 1;else R = mid - 1;}ll attack = 0;ll cnt = m;for (int i = 0; i < n; i++) {if (a[i] < R) continue;ll t = (a[i] - L) / b[i] + 1;if (a[i] - b[i] * (t - 1) == R) t -1;attack += (a[i] * 2 - (t - 1) * b[i]) * t / 2;cnt -= t;}cout << attack + cnt * R << endl;return 0;
}java代码
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;public class Main {static BufferedReader br = new BufferedReader(new InputStreamReader(System.in), 65536);static StringTokenizer tokenizer = new StringTokenizer("");static int maxn = (int) (1e5 + 5);static int[] array = new int[maxn];static int[] facts = new int[maxn];static int n, m;// 二分枚举最后一次攻击力最高能加多少,并且要注意最后的计算不能把等于这个值的直接加在答案里public static void main(String[] args) {n = nextInt(); m = nextInt();for (int i = 0; i < n; i++) {array[i] = nextInt();facts[i] = nextInt();}long ans = 0L;// 二分最后一次技能最多提升了多少攻击力int l = 0, r = (int) 1e6;while (l < r) {int mid = l + r + 1 >> 1;if (check(mid)) l = mid;else r = mid - 1;}int x = l;for (int i = 0; i < n; i++) {if (array[i] >= x) {int cnt = (array[i] - x) / facts[i] + 1;int last = array[i] - (cnt - 1) * facts[i];if (last == x) {cnt--;last += facts[i];}ans += (long) (array[i] + last) * cnt >> 1;m -= cnt;}}ans += (long) m * x;System.out.println(ans);}// 最后一次加攻击力不能到 xpublic static boolean check(int x) {int cnt = 0;for (int i = 0; i < n; i++) {if (array[i] < x) continue;cnt += (array[i] - x) / facts[i] + 1;if (cnt >= m) return true;}return false;}public static String next() {while (!tokenizer.hasMoreTokens()) {try {tokenizer = new StringTokenizer(br.readLine());} catch (IOException e) {e.printStackTrace();}}return tokenizer.nextToken();}public static int nextInt() { return Integer.parseInt(next()); }public static long nextLong() { return Long.parseLong(next()); }
}
python代码
def check(mid): #最后一次技能升级,最多能不能到midcnt = 0 for i in range(n): if a[i] < mid: continue #第i个技能的初值还不够mid,不用这个技能cnt += (a[i] - mid) // b[i] + 1 #第i个技能用掉的次数if cnt >= m: return True #所有技能升级总次数大于等于m次,说明mid设小了return False #所有技能升级总次数小于m次,说明mid设大了n, m = map(int, input().split())
a = [] #存ai
b = [] #存bi
for i in range(n):a_,b_ = map(int,input().split())a.append(a_)b.append(b_)
L,R = 1,1000000 #二分枚举最后一次攻击力最高能加多少
while(L <= R):mid = (L + R) // 2if check(mid): L = mid + 1 #增加midelse: R = mid - 1 #减小mid
attack = 0
cnt = m
for i in range(n):if a[i] < R: continuet = (a[i] - L) // b[i] + 1 #第i个技能升级次数if a[i] - b[i] * (t - 1) == R: t -= 1 #这个技能每次升级刚好等于R,其他技能更好attack += (a[i] * 2 - (t - 1) * b[i]) * t / 2 cnt -= t
print(int(attack) + cnt * R)
相关文章:

<蓝桥杯软件赛>零基础备赛20周--第10周--二分
报名明年4月蓝桥杯软件赛的同学们,如果你是大一零基础,目前懵懂中,不知该怎么办,可以看看本博客系列:备赛20周合集 20周的完整安排请点击:20周计划 每周发1个博客,共20周(读者可以按…...

C++友元类,工厂模式和继承的融合案例
//友元没有继承性,没有传递性,所以在animal中定义友元类是无效的class animal{public:animal(){};virtual ~animal(){};};class Cat:public animal{friend class animalFactory;private:Cat(){}private:string m_name;string m_color;public:void about(){cout<&…...

使用 ?? 重新定义逻辑以获得更严格、更安全的 JavaScript 默认值
使用 ?? 重新定义逻辑以获得更严格、更安全的 JavaScript 默认值 JavaScript 中的 ?? 运算符称为 nullish 合并运算符。该运算符接受任一侧的操作数,并且仅当左侧操作数为空值时才返回右侧操作数。这个运算符绝对是一个较新的运算符,它是在 ES2020 …...
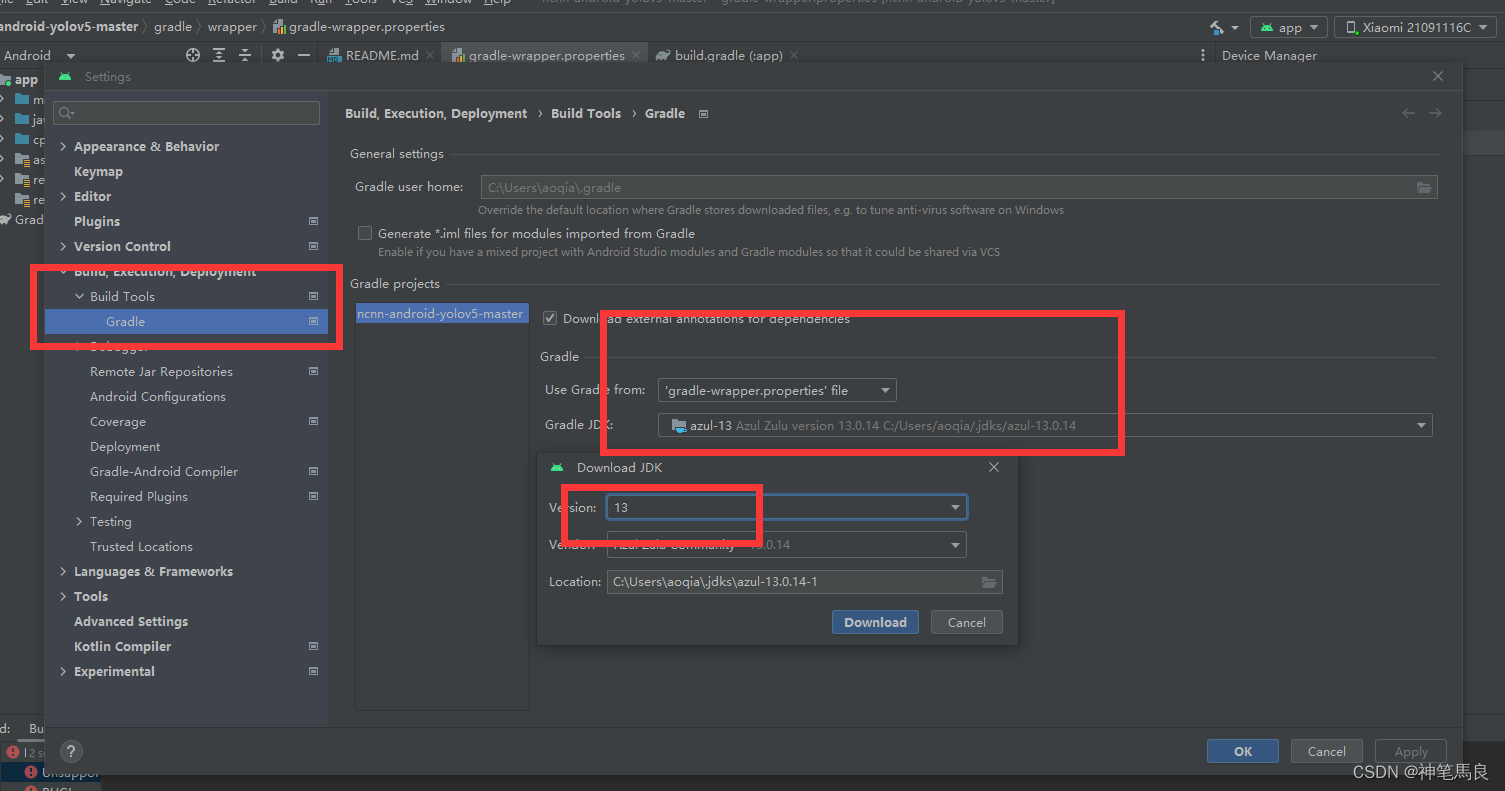
Could not initialize class org.codehaus.groovy.vmplugin.v7.Java7
问题描述:Could not initialize class org.codehaus.groovy.vmplugin.v7.Java7 最近在学习如何将YOLO部署在手机端,出现了许多错误,下面这个错误是手机和电脑连结之后,点击run之后出现的错误。 解决办法:将JDK版本将为…...

Python Django Suit:构建现代化的Django后台管理
概要 Django Suit是一款为Django后台管理提供现代、优雅界面的第三方应用,它致力于提升Django开发者的管理体验。本文将深入介绍Django Suit的安装、配置和高级功能,提供详实的示例代码,帮助大家更好地使用和定制Django后台管理界面。 安装与…...

电子学会C/C++编程等级考试2021年09月(六级)真题解析
C/C++等级考试(1~8级)全部真题・点这里 第1题:双端队列 定义一个双端队列,进队操作与普通队列一样,从队尾进入。出队操作既可以从队头,也可以从队尾。编程实现这个数据结构。 时间限制:1000 内存限制:65535输入 第一行输入一个整数t,代表测试数据的组数。 每组数据的…...

SpringBoot 源码解析
前言 本文只是纯源码分析文章,阅读者需要有Spring或者SpringBoot使用经验。 SpringBoot 源码解析 SpringBoot 源码解析1:环境搭建 SpringBoot 源码解析2:启动流程1 SpringBoot 源码解析3:启动流程2 SpringBoot 源码解析4&#…...

dockerfile---创建镜像
dockerfile创建镜像:创建自定义镜像。 包扩配置文件的创建,挂载点,对外暴露的端口。设置环境变量。 docker镜像的方式: 1、基于官方源进行创建 根据官方提供的镜像源,创建镜像,然后拉起容器。是一个白板,…...

Raspberry PI + Codesys + EtherCAT步进驱动ECR60 Motion功能测试
原文连接:Raspberry PI Codesys EtherCAT步进驱动ECR60 Motion功能测试 – 个人资料收集 (rtplc.com) <div class"post_info_wrapper "> <p class"has-drop-cap">运动控制功能是codesys及EtherCAT通讯的重要功能&am…...
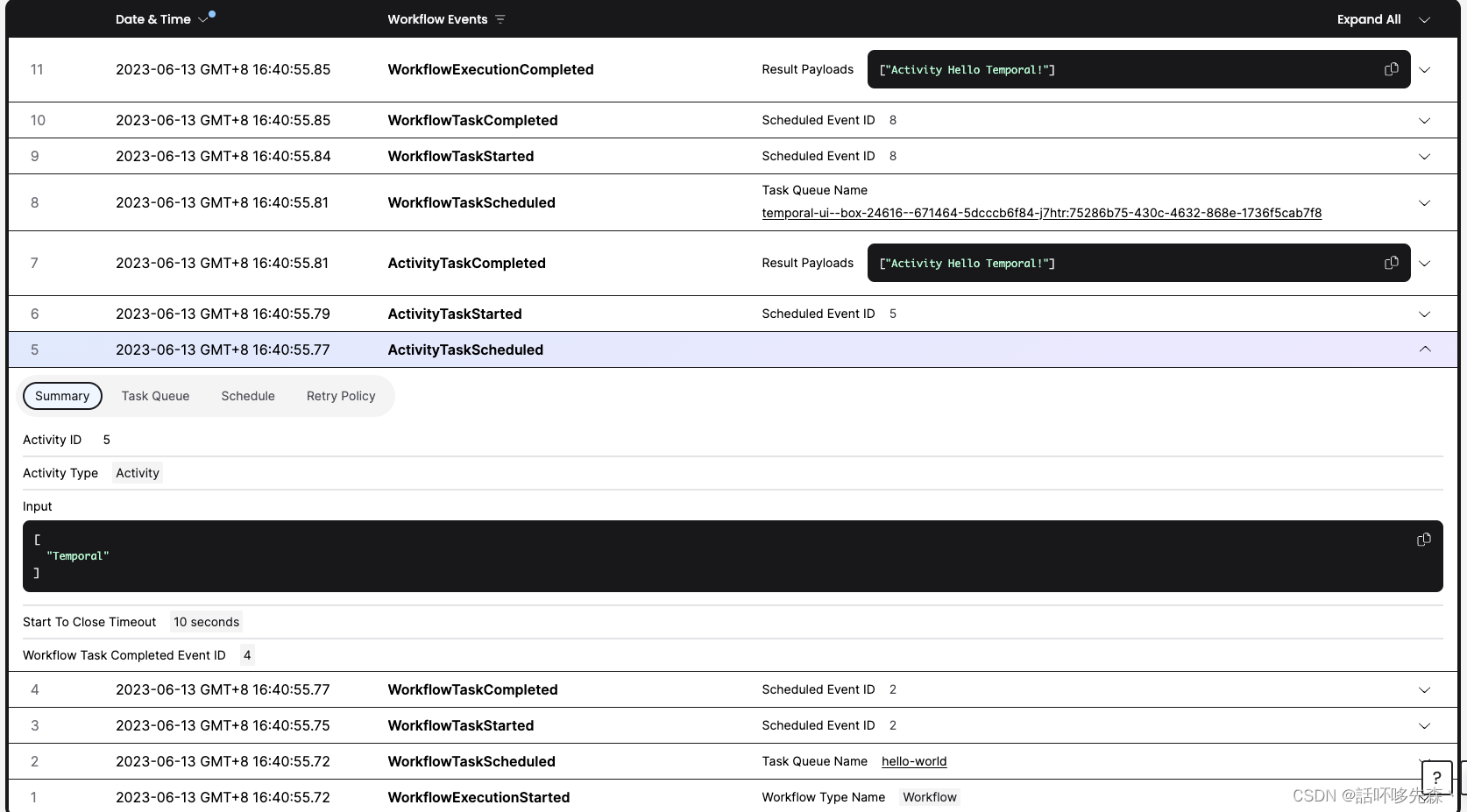
03 Temporal 详细介绍
前言 在后端开发中,大家是否有遇到如下类型的开发场景 需要处理较多的异步事件需要的外部服务可靠性较低需要记录保存某个对象的复杂状态 在以往的开发过程中,可能更多的直接使用数据库、定时任务、消息队列等作为基础,来解决上面的问题。然…...

【算法】【动规】乘积为正数的最长子数组长度
跳转汇总链接 👉🔗算法题汇总链接 1.1 乘积为正数的最长子数组长度 🔗题目链接 给你一个整数数组 nums ,请你求出乘积为正数的最长子数组的长度。 一个数组的子数组是由原数组中零个或者更多个连续数字组成的数组。 请你返回乘积…...
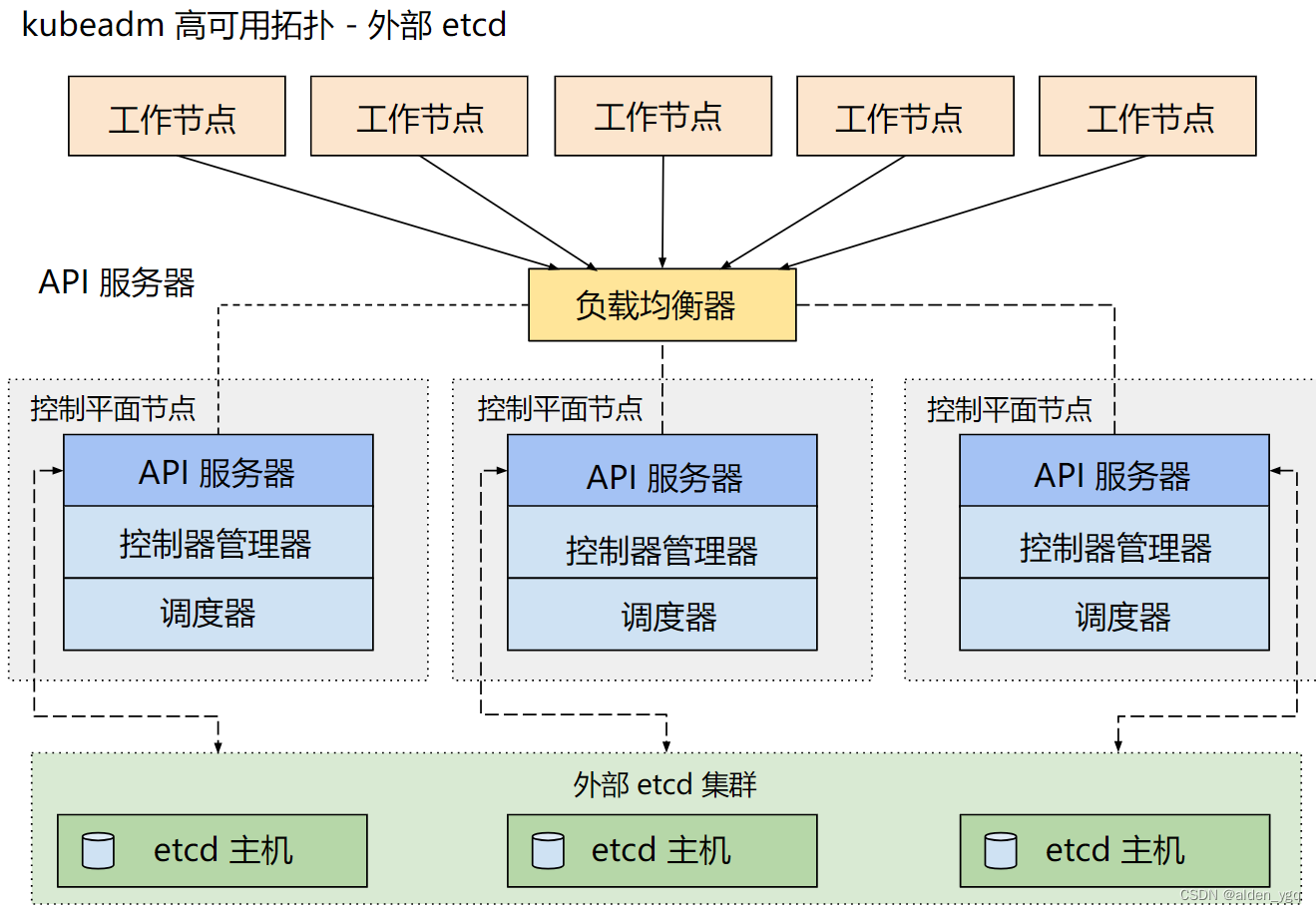
Kubernetes实战(十四)-k8s高可用集群扩容master节点
1 单master集群和多master节点集群方案 1.1 单Master集群 k8s 集群是由一组运行 k8s 的节点组成的,节点可以是物理机、虚拟机或者云服务器。k8s 集群中的节点分为两种角色:master 和 node。 master 节点:master 节点负责控制和管理整个集群…...
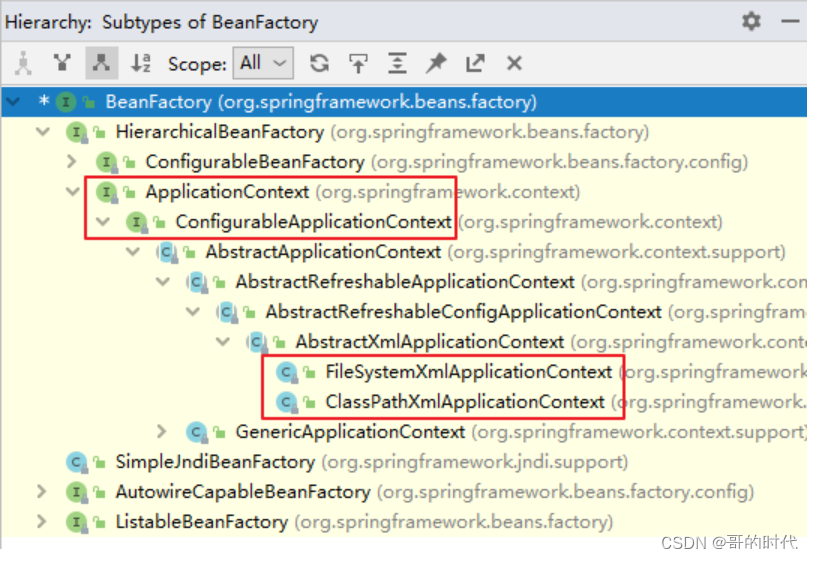
Spring之容器:IOC(1)
学习的最大理由是想摆脱平庸,早一天就多一份人生的精彩;迟一天就多一天平庸的困扰。各位小伙伴,如果您: 想系统/深入学习某技术知识点… 一个人摸索学习很难坚持,想组团高效学习… 想写博客但无从下手,急需…...

【.Net 6.0--通用帮助类--ConvertHelper】
前言 类型转换帮助类,包含下表中的方法: 方法名方法解释ObjToIntobject转intObjToMoneyobject转doubleObjToStringobject转stringObjToDecimalobject转decimalObjToDateobject转datetimeObjToDateSplitYMDobject转datetime(yyyy-MM-dd&…...
)
【加解密】报文签名与加解密,MD5,RSA,AES使用案例(基于 Java)
需要考虑哪些问题? 在进行报文传输时,有两个问题需要考虑: 消息防篡改加密报文 定义消息结构 为了方便后面使用,这里定义消息结构: public static class Message {public String data; //消息public String sign;…...

新建vue3项目
三种方法 一. 第一种方式 1、操作步骤: 创建项目目录 vue create 项目名称选择配置方式 ? Please pick a preset: #选择一个配置 Default ([Vue 3] babel, eslint)Default ([Vue 2] babel, eslint)Manually select …...
出现 Error:Unable to access jarfile xxxx\target\nacos-server.jar 解决方法
目录 1. 问题所示2. 原理分析3. 解决方法1. 问题所示 执行Nacos中的startup.cmd的时候出现闪退,于是在该脚本的最后一行添加pause,查看因为什么原因闪退 出现的bug如下所示:Error:Unable to access jarfile xxxx\target\nacos-server.jar 截图如下所示: 查看内部文件夹,…...
记录一次API报文替换点滴
1. 需求 各位盆友在日常开发中,有没有遇到上游接口突然不合作了,临时需要切换其他接口的情况?这不巧了,博主团队近期遇到了,又尴尬又忐忑。 尴尬的是临时通知不合作了,事前没有任何提醒; 忐忑…...
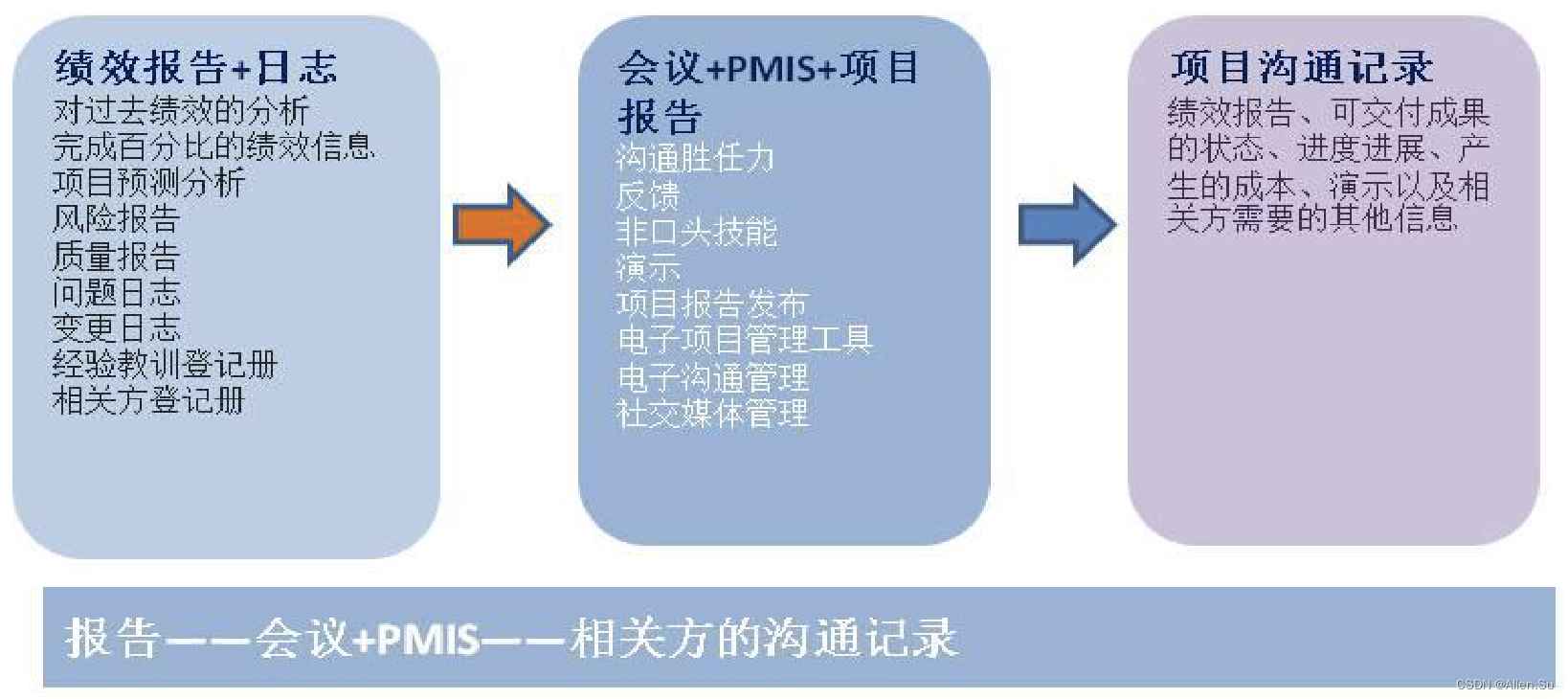
PMP项目管理 - 沟通管理
系列文章目录 PMP项目管理 - 质量管理 PMP项目管理 - 采购管理 PMP项目管理 - 资源管理 PMP项目管理 - 风险管理 现在的一切都是为将来的梦想编织翅膀,让梦想在现实中展翅高飞。 Now everything is for the future of dream weaving wings, let the dream fly in…...

fckeditor编辑器改造示例:增加PRE,CODE控件
查看专栏目录 Network 灰鸽宝典专栏主要关注服务器的配置,前后端开发环境的配置,编辑器的配置,网络服务的配置,网络命令的应用与配置,windows常见问题的解决等。 文章目录 修改方法:1)修改fckco…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...
