【机器学习 | 假设检验系列】假设检验系列—卡方检验(详细案例,数学公式原理推导),最常被忽视得假设检验确定不来看看?

🤵♂️ 个人主页: @AI_magician
📡主页地址: 作者简介:CSDN内容合伙人,全栈领域优质创作者。
👨💻景愿:旨在于能和更多的热爱计算机的伙伴一起成长!!🐱🏍

摘要: 本系列旨在普及那些深度学习路上必经的核心概念,【机器学习 | 假设检验系列】假设检验系列—卡方检验(详细案例,数学公式原理推导),最常被忽视得假设检验确定不来看看?
该文章收录专栏
[✨— 《深入解析机器学习:从原理到应用的全面指南》 —✨]
假设检验(Hypothesis Testing)
假设检验(Hypothesis Testing)是狭义数据分析中的一种常用方法,用于检验关于总体参数的假设。它可以帮助我们判断样本数据与某个假设之间是否存在显著差异。假设检验通常涉及以下步骤:
-
建立原假设(Null Hypothesis)和备择假设(Alternative Hypothesis):原假设是关于总体参数的某种假设,备择假设是与原假设相对立的假设。
-
选择适当的假设检验方法:根据研究问题和数据类型,选择适合的假设检验方法,例如t检验、卡方检验、ANOVA等。
-
计算检验统计量:根据所选的假设检验方法,计算得到相应的检验统计量。
-
确定显著性水平:设定显著性水平(例如0.05),表示拒绝原假设的阈值。
p 值(p-value)是用于衡量统计假设检验结果的一个概率指标(可以理解为是一个用来衡量观察到的数据与原假设之间的矛盾程度的指标)。它表示观察到的数据或更极端情况下,基于原假设(零假设)成立的情况下发生的概率。
-
进行假设检验:根据检验统计量和显著性水平,判断样本数据是否足够证据支持或拒绝原假设。
-
得出结论:根据假设检验的结果,得出关于总体参数的结论,并进行解释。
假设检验可以帮助我们验证关于总体参数的假设,从而在数据分析过程中提供可靠的推断和结论。因此,它可以被视为狭义数据分析的一部分。
| 名称 | 介绍 | 优缺点 |
|---|---|---|
| 正态性检验 (Normality Test) | 正态性检验用于确定数据是否符合正态分布。常用的正态性检验方法包括Kolmogorov-Smirnov检验、Shapiro-Wilk检验和Anderson-Darling检验等。 | 优点:可以帮助确定数据是否适合使用基于正态分布的统计方法。缺点:对于大样本数据,即使微小的偏差也可能导致拒绝正态性假设。 |
| 相关性检验 (Correlation Test) | 相关性检验用于确定两个变量之间的相关性。常用的相关性检验方法包括Pearson相关系数、Spearman等级相关系数和Kendall秩相关系数。(该检验算法只能用于数值型,而不能用于类别型) | 优点:可以衡量变量之间的线性或非线性关系。缺点:相关性并不能说明因果关系,只是指示变量之间的关联程度。 |
| 异常值检测 (Outlier Detection) | 异常值检测用于识别在数据集中具有异常特征的数据点。常用的异常值检测方法包括基于统计学的Z-score方法、3σ原则、箱线图方法和基于距离的方法(如DBSCAN)。 | 优点:可以帮助识别异常值,对于数据清洗和异常数据处理很有用。缺点:某些方法对于多维数据和高维数据的处理较为困难。 |
| 方差分析 (Analysis of Variance, ANOVA) | 方差分析用于比较两个或多个组之间的均值是否有显著差异。常用的方差分析方法包括单因素方差分析和多因素方差分析。 | 优点:适用于比较多个组之间的差异,提供了有效的统计推断。缺点:对于非正态分布的数据和小样本容量可能不适用。 |
| t检验 (t-Test) | t检验用于比较两个组之间的均值是否有显著差异。常用的t检验方法包括独立样本t检验和配对样本t检验。 | 优点:简单易用,适用于小样本数据。缺点:对于非正态分布的数据可能不准确,对异常值敏感。 |
| 卡方检验 (Chi-Square Test) | 卡方检验用于比较两个或多个分类变量之间的关联性。常用的卡方检验方法包括卡方独立性检验和卡方拟合度检验。 | 优点:适用于分类数据的统计推断,用于检验观察频数与期望频数之间的差异。缺点:对于样本量较小或期望频数较低的情况可能不准确。 |
| 平稳性检验(Stationarity Test) | 用于检验时间序列数据是否具有平稳性的统计检验方法。平稳性是指时间序列的统计特性在不同时间段上保持不变。 | 优点:可以判断时间序列数据是否具有平稳性,为后续时间序列分析提供基础。 缺点:不同的平稳性检验方法可能会得出不同的结果,需要综合考虑多个检验方法。 |
| 白噪声检验(White Noise Test) | 用于检验时间序列数据是否符合白噪声过程的统计检验方法。白噪声是指具有相互独立且均值为零的随机变量序列,没有序列之间的相关性。 | 优点:可以检验时间序列数据是否具有随机性和独立性,对于时间序列分析的合理性很重要。 缺点:不同的白噪声检验方法可能会得出不同的结果,需要综合考虑多个检验方法。 |
卡方检验
卡方检验(Chi-square test)是由卡方分布(Chi-square distribution)衍生而来的一种统计方法。卡方分布最初由英国统计学家卡尔·皮尔逊(Karl Pearson)于1900年提出,提供了一种有效的方法来分析和解释离散型数据的关联性,帮助研究人员得出结论和推断。卡方检验是基于卡方分布的概念发展而来的,于此后的统计学和应用领域被广泛使用,例如医学研究、社会科学调查、市场研究等。
卡方统计量的计算基于观察频数与期望频数的差异程度,差异越大,卡方统计量的值就越大。卡方统计量的分布与自由度有关,可以使用卡方分布表或统计软件来确定其对应的显著性水平。通常情况下,我们选择一个显著性水平(例如0.05),如果计算得到的卡方统计量大于对应自由度和显著性水平的临界值,就拒绝原假设,认为观察到的频数与期望频数之间存在显著差异,即变量之间存在关联或独立性被拒绝。
假设我们有一个二维列联表(contingency table),其中包含了两个分类变量的观测频数。表格如下所示:
| 变量B=0 | 变量B=1 | 总计 | |
|---|---|---|---|
| 变量A=0 | a | b | a+b |
| 变量A=1 | c | d | c+d |
| 总计 | a+c | b+d | a+b+c+d |
其中,a、b、c、d 分别表示四个格子中的观测频数。
卡方检验的原假设(null hypothesis)是:变量A和变量B是相互独立的,即它们之间没有显著关联。备择假设(alternative hypothesis)是:变量A和变量B是相关联的,即它们之间存在显著关联。
卡方检验的步骤如下:
步骤 1:计算期望频数(expected frequencies)
首先,我们需要计算每个单元格的期望频数,即在假设变量A和变量B是独立的情况下,每个单元格中的预期频数。期望频数的计算公式如下:
卡方检验中的期望频数是根据原假设(变量A和变量B是独立的)(这很重要!!)来计算的。预期频数的计算采用了边际总频数和行、列边际频数的乘积。
假设变量A和变量B是独立的,那么变量A的取值(0或1)与变量B的取值(0或1)之间应该没有关联。因此,我们可以将总体中相应的比例应用于每个格子中的边际频数。
考虑到每个格子中的边际频数,我们可以计算期望频数 E i j E_{ij} Eij,其中 i 表示行索引,j 表示列索引:
E i j = ( a + b ) ( a + c ) a + b + c + d E_{ij} = \frac{{(a+b)(a+c)}}{{a+b+c+d}} Eij=a+b+c+d(a+b)(a+c)
这个计算公式的推导如下:
- 首先,我们考虑变量A的取值为0的情况。在这种情况下,变量A=0的概率是 a + b a + b + c + d \frac{{a+b}}{{a+b+c+d}} a+b+c+da+b(a+b 是变量A=0的边际频数,a+b+c+d 是总体的边际频数)。同样地,变量B=0的概率是 a + c a + b + c + d \frac{{a+c}}{{a+b+c+d}} a+b+c+da+c。由于我们假设变量A和变量B是独立的,我们可以将这两个概率相乘得到变量A=0且变量B=0的联合概率: ( a + b ) ( a + c ) ( a + b + c + d ) 2 \frac{{(a+b)(a+c)}}{{(a+b+c+d)^2}} (a+b+c+d)2(a+b)(a+c)。
- 接下来,我们将联合概率乘以总体的边际频数 ( a + b + c + d ) (a+b+c+d) (a+b+c+d),以获得变量A=0且变量B=0的期望频数 E 00 E_{00} E00。因此,我们得到了公式中的分子部分: ( a + b ) ( a + c ) a + b + c + d \frac{{(a+b)(a+c)}}{{a+b+c+d}} a+b+c+d(a+b)(a+c)。类似地,我们可以推导出其他格子的期望频数。
这样,我们就得到了卡方检验中期望频数的计算公式。
需要注意的是,期望频数是在原假设下计算的,假设变量A和变量B是独立的。如果观测频数与期望频数之间存在显著差异,那么我们将拒绝原假设,认为变量A和变量B之间存在显著关联。
E i j = ( a + b ) ( a + c ) a + b + c + d E_{ij} = \frac{{(a+b)(a+c)}}{{a+b+c+d}} Eij=a+b+c+d(a+b)(a+c)
其中, E i j E_{ij} Eij 表示第 i 行第 j 列单元格的期望频数。(这里的i = 1, j = 1)
步骤 2:计算卡方统计量(chi-square statistic)
接下来,我们计算卡方统计量,用于衡量观测频数与期望频数之间的差异。卡方统计量的计算公式如下:
χ 2 = ∑ ( O i j − E i j ) 2 E i j \chi^2 = \sum \frac{{(O_{ij} - E_{ij})^2}}{{E_{ij}}} χ2=∑Eij(Oij−Eij)2
其中, χ 2 \chi^2 χ2 表示卡方统计量, O i j O_{ij} Oij 表示第 i 行第 j 列单元格的观测频数, E i j E_{ij} Eij 表示第 i 行第 j 列单元格的期望频数。
步骤 3:计算自由度(degrees of freedom)
自由度是卡方统计量中可以自由变动的观测值的数量。在卡方检验中,自由度的计算公式如下(以在卡方分布表中查找对应的临界值或计算 p 值):
自由度的公式是根据卡方检验中的二维列联表的维度来确定的。在二维列联表中,行和列的数量分别为 r 和 c。
假设我们有一个 r 行 c 列的二维列联表。自由度的计算基于以下原则:
- 在行方向上,我们可以自由选择每个单元格的观测频数,但是要满足行边际频数。
- 在列方向上,我们也可以自由选择每个单元格的观测频数,但是同样要满足列边际频数。
因此,对于每个单元格,我们有一个自由度。总的自由度等于所有单元格的自由度之和。
在二维列联表中,行和列的边际频数已知,所以我们只需要确定每个单元格的观测频数。一旦我们选择了 r 行 c 列个单元格的观测频数,其他单元格的观测频数就会被固定。
为了保持边际频数不变,我们需要根据边际频数的限制条件来选择观测频数。对于二维列联表,有两个限制条件,一个是行边际频数,另一个是列边际频数。
考虑到这些限制条件,我们可以自由选择的单元格的个数为 (r-1) × (c-1)。这是因为,一旦我们选择了其中一个单元格的观测频数,改行列的其他单元格的观测频数将根据限制条件被固定。
d f = ( r − 1 ) ( c − 1 ) df = (r-1)(c-1) df=(r−1)(c−1)
其中, r r r 表示行数, c c c 表示列数。
步骤 4:计算 p 值(p-value)
我们根据卡方统计量和自由度计算 p 值。一种常用的方法是将卡方统计量与自由度对应的卡方分布进行比较,并计算出落入更极端区域的概率。这可以通过查找卡方分布表或使用统计软件进行计算。在实际应用中,通常使用软件包(如Python的SciPy库或R语言中的stats包)来计算 p 值。
根据给定的显著性水平(significance level),通常选择 p 值与显著性水平进行比较。如果 p 值小于显著性水平,通常为0.05,我们可以拒绝原假设,认为变量A和变量B之间存在显著关联;否则,我们接受原假设,认为变量A和变量B之间没有显著关联。
下面则是一个真实简单的案例来说明卡方检验的流程和原理:
假设我们想研究男性和女性之间是否存在喜欢不同类型电影的差异。我们随机选择了100个男性和100个女性,并记录了他们对三种类型电影的喜好(A类、B类和C类)。
观察到的频数如下:
A类 B类 C类
男性 30 35 35
女性 45 25 30
首先,我们需要建立假设。在这里,我们的原假设是“男性和女性对不同类型电影的喜好没有差异”。备择假设是“男性和女性对不同类型电影的喜好有差异”。
接下来,我们计算期望频数。期望频数是基于原假设,假设男性和女性对电影类型的喜好是独立的。我们可以通过公式计算期望频数如下:
A类 B类 C类
男性 37.5 32.5 30
女性 37.5 32.5 30
然后,我们计算卡方统计量。卡方统计量衡量了观察频数与期望频数之间的差异,我们可以计算出卡方统计量为:
卡方统计量 = [(30-37.5)²/37.5] + [(35-32.5)²/32.5] + [(35-30)²/30] + [(45-37.5)²/37.5] + [(25-32.5)²/32.5] + [(30-30)²/30] ≈ 6.8
最后,我们需要确定卡方统计量的显著性水平。我们使用自由度来确定显著性水平,在这个例子中,自由度为 (2-1) × (3-1) = 2。
我们可以使用卡方分布表或统计软件来查找卡方统计量对应的显著性水平。假设我们使用了显著性水平为0.05,自由度为2,我们发现卡方统计量的临界值为5.99。由于6.8 > 5.99,我们可以拒绝原假设,接受备择假设,即男性和女性对不同类型电影的喜好存在差异。
临界值是在显著性水平下拒绝原假设的界限。如果观察到的卡方统计量大于临界值,我们可以拒绝原假设。

🤞到这里,如果还有什么疑问🤞🎩欢迎私信博主问题哦,博主会尽自己能力为你解答疑惑的!🎩🥳如果对你有帮助,你的赞是对博主最大的支持!!🥳
相关文章:

【机器学习 | 假设检验系列】假设检验系列—卡方检验(详细案例,数学公式原理推导),最常被忽视得假设检验确定不来看看?
🤵♂️ 个人主页: AI_magician 📡主页地址: 作者简介:CSDN内容合伙人,全栈领域优质创作者。 👨💻景愿:旨在于能和更多的热爱计算机的伙伴一起成长!!&…...

RealBasicVSR高清处理视频
autodl做了镜像:高清RealBasicVSR 首先在剪映将视频剪好导出,最多是720像素的,不然后面超分的时候会爆显存。剪映视频也最好是双数帧数结尾的,不然超分的时候单数图片会报错->RuntimeError: non-empty 3D or 4D input tensor …...

晚期食管癌肿瘤治疗线程分类
文章目录 1、肿瘤治疗的线数1.1 基础概念1.2 线程定义1.3 如何计算治疗线数 2 食管癌治疗指南2.1 食管癌诊疗指南2.1 CSCO 本文前半部分主要来源于参考文件1,其余部分来源于官方指南。无原创内容,全部为摘要。 1、肿瘤治疗的线数 1.1 基础概念 抗肿瘤药…...
高效营销系统集成:百度营销的API无代码解决方案,提升电商与广告效率
百度营销API连接:构建无代码开发的高效集成体系 在数字营销的高速发展时代,企业追求的是快速响应市场的能力以及提高用户运营的效率。百度营销API连接正是为此而生,它通过无代码开发的方式,实现了电商平台、营销系统和CRM的一站式…...
网络基础(十一):VRRP原理与配置
目录 前言: 1、VRRP的基本概述 2、VRRP的基本原理 2.1VRRP的基本结构 2.2设备类型 2.3状态机 2.4VRRP路由器的抢占功能 2.5VRRP路由器的优先级 2.6VRRP工作原理 2.7主备路由器的工作内容 3、VRRP的基本配置 3.1配置主路由器和备用路由器 3.2配置PC1与P…...
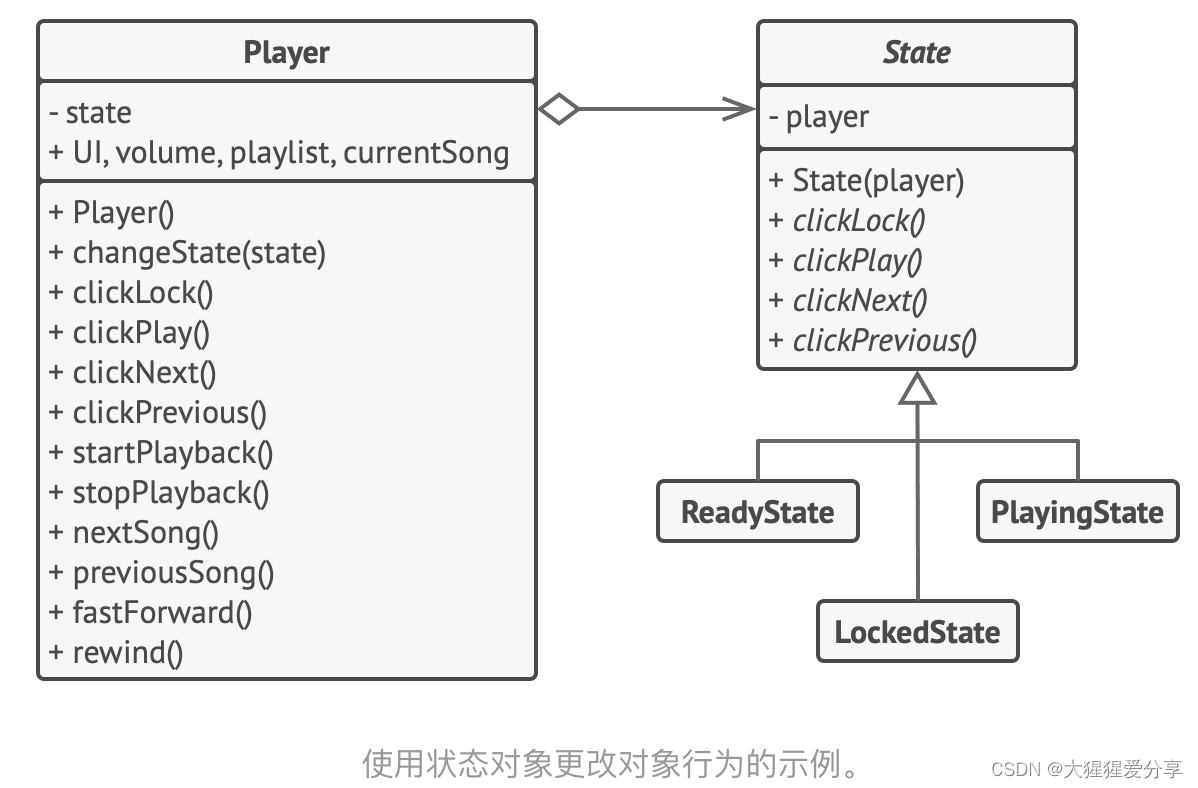
设计模式——状态模式
引言 状态模式是一种行为设计模式, 让你能在一个对象的内部状态变化时改变其行为, 使其看上去就像改变了自身所属的类一样。 问题 状态模式与有限状态机 的概念紧密相关。 其主要思想是程序在任意时刻仅可处于几种有限的状态中。 在任何一个特定状态中…...

2020-XNUCA babyv8
做的第一道存在指针压缩机制的V8题,通过小越界写修改length构造大越界读写,然后利用arraybuffer的backing store构造任意地址写,利用wasm rwx段地址的特点以及堆空间的分布,搜索到rwx段的具体地址,然后利用任意地址写将…...

货物数据处理pandas版
1求和 from openpyxl import load_workbook import pandas as pddef print_hi(name):# Use a breakpoint in the code line below to debug your script.print(fHi, {name}) # Press CtrlF8 to toggle the breakpoint.# Press the green button in the gutter to run the scr…...
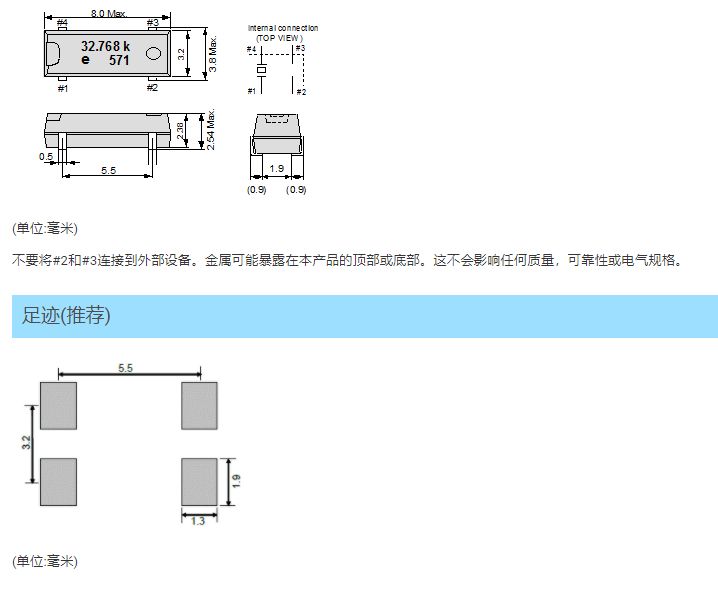
MC-30A (32.768 kHz用于汽车应用的晶体单元)
MC-30A 32.768 kHz用于汽车应用的晶体,车规晶振中的热销型号之一。该款石英晶体谐振器,可以在-40 to 85 C的温度内稳定工作,能满足起动振动的要求。同时满足AEC-Q200无源元件质量标准认证,满足汽车仪表系统的所有要求。 频率范围…...
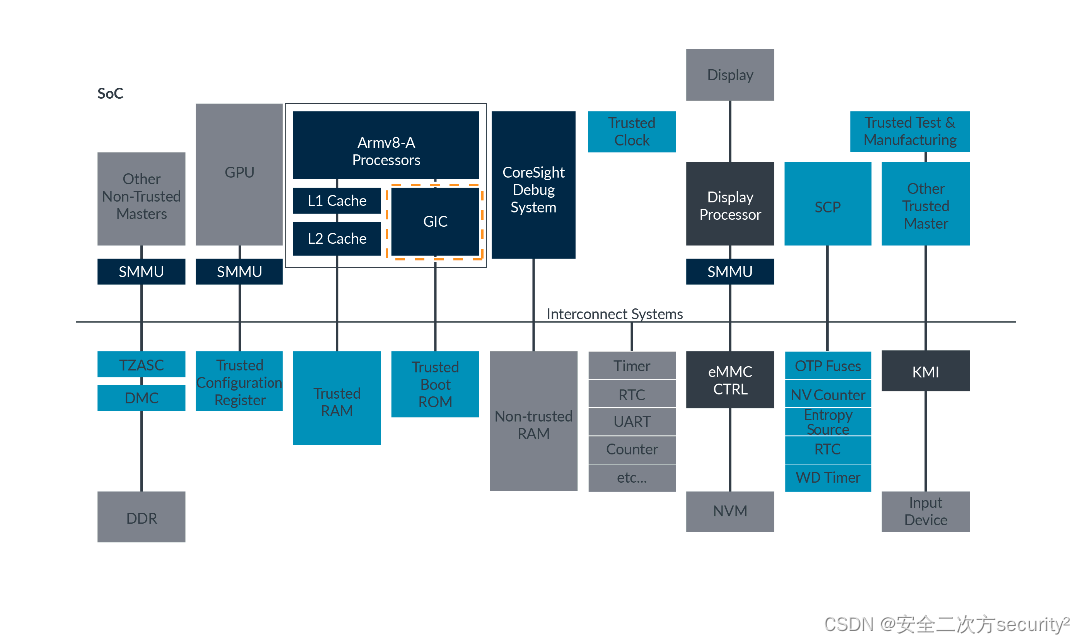
TrustZone之其他设备及可信基础系统架构
一、其他设备 最后,我们将查看系统中的其他设备,如下图所示: 我们的示例TrustZone启用的系统包括一些尚未涵盖的设备,但我们需要这些设备来构建一个实际的系统。 • 一次性可编程存储器(OTP)或保险丝 这些是一旦写入就无法更改的存储器。与每个芯片上都包含相同…...
自由编程学习资源:free-programming-books
最近,我发现了一个在GitHub上备受欢迎的项目,它为程序员和编程爱好者提供了丰富、免费且高质量的学习资料,这就是"free-programming-books"。目前,这个项目在GitHub上已经有305k的star,显示出它在开发者社区…...

饥荒Mod 开发(十三):木牌传送
饥荒Mod 开发(十二):一键制作 饥荒Mod 开发(十四):制作屏幕弹窗 一键传送源码 饥荒的地图很大,跑地图太耗费时间和饥饿值,如果大部分时间都在跑图真的是很无聊,所以需要有一个能够传送的功能,不仅可以快速…...
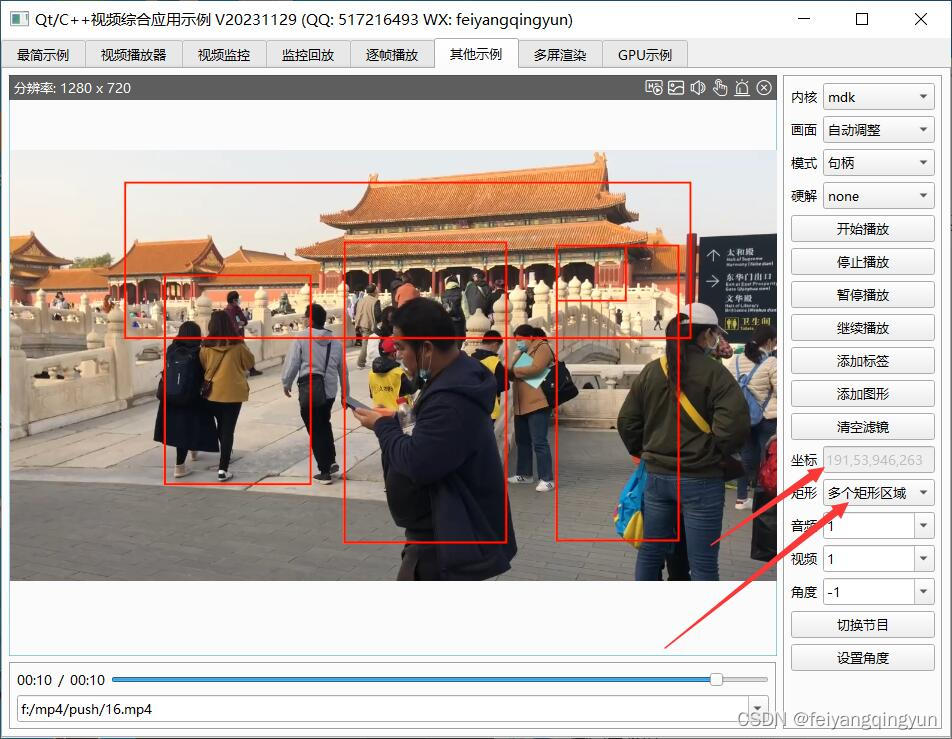
Qt/C++音视频开发60-坐标拾取/按下鼠标获取矩形区域/转换到视频源真实坐标
一、前言 通过在通道画面上拾取鼠标按下的坐标,然后鼠标移动,直到松开,根据松开的坐标和按下的坐标,绘制一个矩形区域,作为热点或者需要电子放大的区域,拿到这个坐标区域,用途非常多࿰…...

Java实现订单超时未支付自动取消的8种方法总结
Java实现订单超时未支付自动取消的8种方法总结 定时轮询 数据库定时轮询方式,实现思路比较简单。启动一个定时任务,每隔一定时间扫描订单表,查询到超时订单就取消。优点:实现简单。缺点:轮询时间间隔不好确定&#x…...

android动态权限申请并展示权限使用说明
# ExplainPermissions 动态权限申请并展示权限使用说明 随着工信部对APP的一系列整治,现在用户对于APP在使用时动态申请的权限是比较敏感的,为了更好的用户体验,我们可以在权限动态申请的时候一并向用户展示所需要申请权限的使用说明。这样用…...
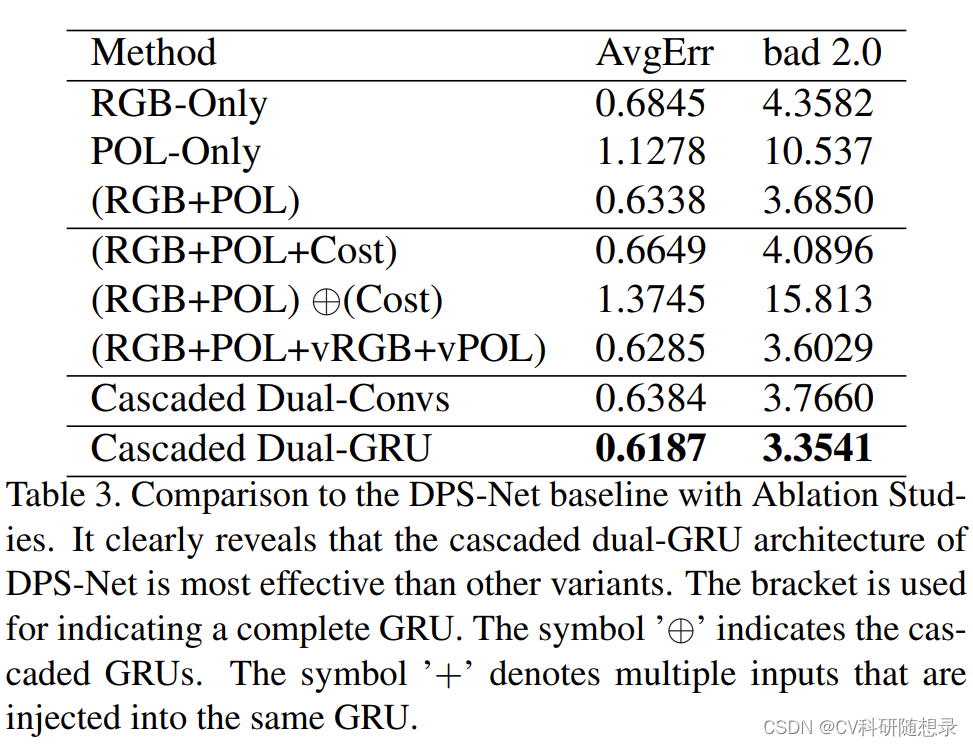
论文阅读《DPS-Net: Deep Polarimetric Stereo Depth Estimation》
论文地址:https://openaccess.thecvf.com/content/ICCV2023/html/Tian_DPS-Net_Deep_Polarimetric_Stereo_Depth_Estimation_ICCV_2023_paper.html 概述 立体匹配模型难以处理无纹理场景的匹配,现有的方法通常假设物体表面是光滑的,或者光照是…...
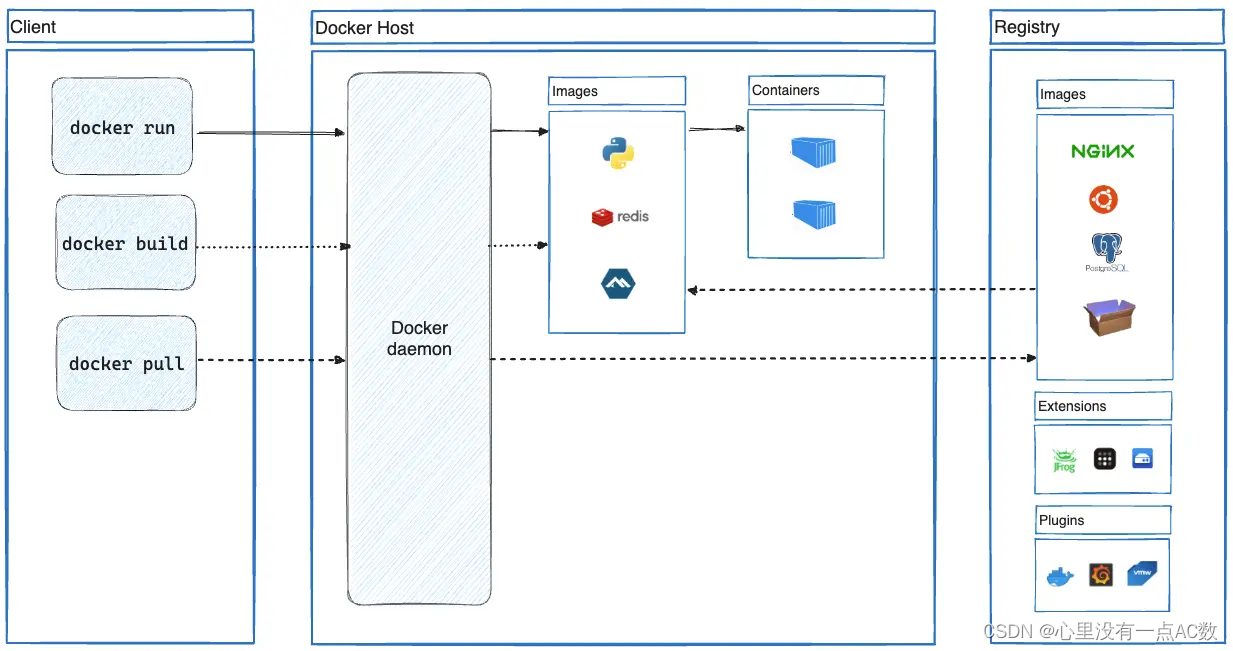
docker文档转译1
写在最前面 本文主要是转译docker官方文档。主题是Docker overview,这里是链接 Docker概述 Docker是一个用于开发、发布和运行应用程序的开放平台。Docker使你能够将应用程序与基础设施分离,从而可以快速交付软件。你可以使用相同的方法像管理应用程序…...
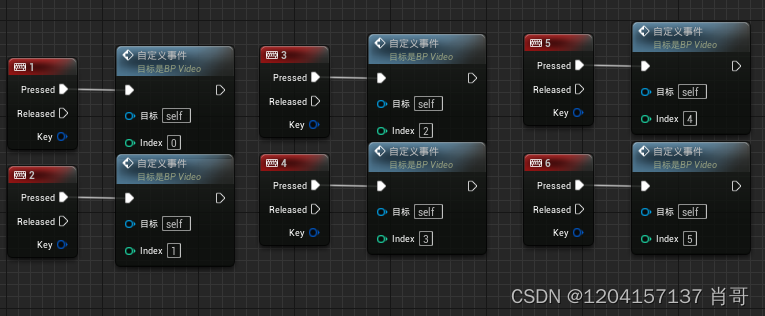
UE4 图片环形轮播 蓝图
【需求】 图片环形轮播 任意图片之间相互切换 切换图片所需时间均为1s 两个图片之间切换使用就近原则 播放丝滑无闪跳 【Actor的组成】 每个图片的轴心都在原点 【蓝图节点】...
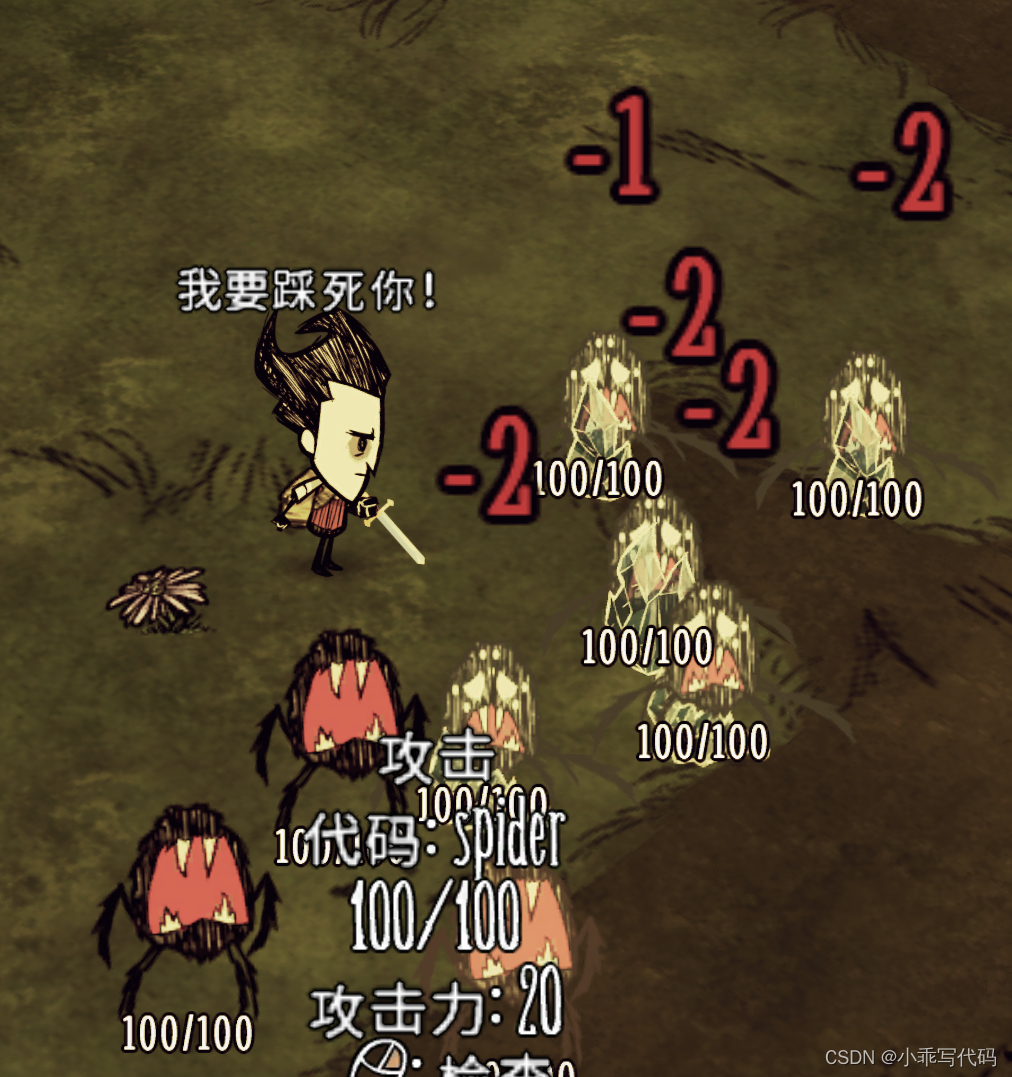
饥荒Mod 开发(十):制作一把AOE武器
饥荒Mod 开发(九):物品栏排列 饥荒Mod 开发(十一):修改物品堆叠 前面的文章介绍了很多基础知识以及如何制作一个物品,这次制作一把武器,装备之后可以用来攻击怪物。 制作武器贴图和动画 1.1 制作贴图。 先准备一张武器的贴图&a…...

微服务实战系列之ZooKeeper(下)
前言 通过前序两篇关于ZooKeeper的介绍和总结,我们可以大致理解了它是什么,它有哪些重要组成部分。 今天,博主特别介绍一下ZooKeeper的一个核心应用场景:分布式锁。 应用ZooKeeper Q:什么是分布式锁 首先了解一下&…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...
