【CCF BDCI 2023】多模态多方对话场景下的发言人识别 Baseline 0.71 Slover 部分
【CCF BDCI 2023】多模态多方对话场景下的发言人识别 Baseline 0.71 Slover 部分
- 概述
- Solver 在多模态发言人识别中的作用
- Solver 在多模态发言人识别中的重要性
- Solver 的工作原理
- 二次规划
- 二次规划的基本形式
- 二次规划的特点
- 二次规划在多模态发言中的应用 (我的理解)
- 代码详解
- 数据转化
- 目标函数和约束设定
- 约束条件的设定
- CVXPY 和 Gurobi 求解
- CVXPY
- Gurobi
- CVXPY 和 Gurobi 求解优化问题
- Citation
概述
现今技术日新月异, Artificial Intelligence 的发展正在迅速的改变我们的生活和工作方式. 尤其是在自然语言处理 (Natural Linguistic Processing) 和计算机视觉 (Computer Vision) 等领域.
传统的多模态对话研究主要集中在单一用户与系统之间的交互, 而忽视了多用户场景的复杂性. 视觉信息 (Visual Info) 往往会被边缘化, 仅作为维嘉信息而非对话的核心部分. 在实际应用中, 算法需要 “观察” 并与多个用户的交互, 这些用户有可能不是当前的发言人.
【CCF BDCI 2023】多模态多方对话场景下的发言人识别, 核心思想是通过多轮连续对话的内容和每轮对应的帧, 以及对应的人脸 bbox 和 name label, 从每轮对话中识别出发言人 (speaker).
Baseline 的代码分为三个文件, 分别为convex_optimization.py, dialog_roberta-constrasive.py, finetune_cnn-multiturn.py. 下面小白我就来带大家详解一下 Solver 部分.
Solver 在多模态发言人识别中的作用
求解器 (Solver) 在多模态发言人识别中的作用是整合和分析来自不同模态的数据, 如食品中的视觉信息和剧本中的文本信息. Slover 的任务是从这些复杂的数据中提取有用的信息, 并最终确定每个对话中的发言人 (Speaker).

Solver 在多模态发言人识别中的重要性
求解器的三大要点:
- 整合多模态数据: Solver 能够处理来自不同源的数据, 在这个赛题中为 CNN 和 NLP 的输出, 为识别提供不同的视角
- 优化决策过程: 通过应用数学和统计的方法, Solver 能够在众多潜在的发言人 (Potential) 中找到最优解
- 提高准确性:相比单一模态分析 (CNN or NLP or Audio, Solver 可以综合考虑多种信息, 先出提高发言人识别的准确率 (可以理解为类似 Bagging 算法)
Solver 的工作原理
Solver 通常采用数字优化技术, 如这次用到的二次规划 (Quadratic Programming), 来解决发言人识别问题. 首先将两个模型的输出转化为数学问题中的参数, 然后用过优化算法寻找这些参数的最优组合, 从而确定发言人 (Speaker).
二次规划
首先声明一下, 小白我是小学毕业, 数学水平停留在2x + 1 = 5的阶段, 下面的内容是基于网上内容 + 我的粗浅理解, 有不对的地方希望大家指正.
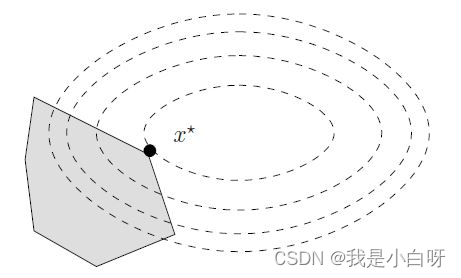
二次规划 (Quadratic Programming). 是一种特殊类型的数学优化问题, 涉及到一个二次目标函数和一系列线性约束.
二次规划的基本形式
二次规划问题可以形式化为下面的数学模型:
- 目标函数: f ( x ) = 1 2 x T Q x + c T x f(x) = \frac{1}{2} x^T Q x + c^T x f(x)=21xTQx+cTx
- 约束条件: A x ≤ b Ax \leq b Ax≤b
其中, x x x 是需要优化的变量向量, Q Q Q 是一个堆成矩阵, c c c 是一个向量, A A A 是一个矩阵, b b b 是一个向量. 目标是找到 x x x 的值, 使得目标函数 f ( x ) f(x) f(x)最大或最小化, 同时满足所有的线性约束条件.
二次规划的特点
二次规划的特点:
- 目标函数的二次性: 二次规划的核心特点是其目标函数是变量的二次函数. 这意味着目标函数可以有一个独特的最大值或最小值, 取决于矩阵 Q 的性质.
- 线性约束: 尽管目标函数是二次的, 但所有的约束都是线性的. 这些约束定义了一个可行域, 优化必须在这个域内
- 凸性: 如果矩阵 Q Q Q 是半正定的, 哪儿二次规划问题是凸的. 凸二次规划保证了全局最优解的存在
二次规划在多模态发言中的应用 (我的理解)
在多模态发言人识别 (MMSI) 的上下文中, 二次规划 (Quadratic Programming) 用于整合来自不同模型 (CNN & Roberta) 的信息, 并找到最佳的发言人分配方案.
这里的目标函数通常包括两部分:
- 基于视觉信息, CNN 输出
- 基于文本信息, Roberta 输出
通过优化这个组合目标函数, Solver 能够在满足一定约束条件的情况下, 分配最可能的发言人 (Speaker).
代码详解
主要步骤:
- 数据转化: 用与将 CNN 和 Roberta / Deberta 的模型输出转化为优化问题所需的格式
- 目标函数和约束的设定
- 优化问题的求解: 通过 Gurobi 求解器求解
- 优化过程: 确保只有一个发言人被选中
- 获取结果
数据转化
def convert_cnn_preds_to_matrix(frame_names_list, cnn_scores, label='pred'):matrix_list, mappings_list = [], []for frame_names in frame_names_list:scores = [cnn_scores.get(frame_name, {}) for frame_name in frame_names]speakers = set(sum([list(i.keys()) for i in scores], list()))speaker_id_mappings = {speaker: i for i, speaker in enumerate(speakers)}matrix = np.zeros((len(frame_names), len(speakers)))for i, score_dict in enumerate(scores):for speaker, score in score_dict.items():matrix[i][speaker_id_mappings[speaker]] = score[label]matrix_list.append(matrix)mappings_list.append(speaker_id_mappings)return matrix_list, mappings_list
- 输入: frame_names_list (帧名) 和 cnn_scores (CNN 预测分数)
- 映射: 将每个帧中出现的发言人分配一个索引, 映射到
speaker_id_mappings - 构建矩阵: 对于每个对话, 初始化一个全 0 矩阵, 行等于帧数, 列等于发言人数量. 遍历每个帧的 score, 根据映射将 speaker 对应的分数放到矩阵对应的位置
- 输出:
- 矩阵列表: 每个对话准话后的矩阵
- 映射列表: 每个对话 speaker 到索引的映射
目标函数和约束设定
def solve(cnn_scores, roberta_scores):'''cnn_scores: matrix of shape [n, m]roberta_scores: matrix of shape [n, n]where m = num_speakers, n = num_sents'''n, m = cnn_scores.shapex = cp.Variable(np.prod(cnn_scores.shape), boolean=True)constraints = []for i in range(n):constraints.append(cp.sum(x[i*m: i*m+m]) == 1)cnn_objective = cnn_scores.reshape(-1).T @ x.Tnew_roberta_scores = np.zeros((n*m, n*m))for i in range(n):for j in range(n):for k in range(m):new_roberta_scores[i*m+k, j*m+k] += roberta_scores[i, j]roberta_objecive = cp.quad_form(x, new_roberta_scores) * (1/2)objective = cnn_objective + roberta_objeciveproblem = cp.Problem(cp.Maximize(objective), constraints)problem.solve(solver='GUROBI')return x.value.reshape(n, m), problem.status
- 变量定义: 定义决策变量
x, 是一个布尔型变量的数组, 其余长度等于cnn_scores矩阵的元素总数. 这个变量代表了每个句子选择每个发言人的决策 - CNN 目标函数:
cnn_objective是通过将cnn_scores矩阵展平鱼决策变量x的专职相乘得到的. 这部分代表了选择特定发言人的奖励 - Roberta 目标函数:
new_roberta_scores: n ∗ m × n ∗ m n*m \times n*m n∗m×n∗m, 该矩阵是对roberta_scores的扩展, 用于表示不同句子之间的相似度roberta_objective是通过对决策变量x应用二次形式得到的, 代表了选择相同发言人的奖励
- 总目标函数: 最终的目标函数
objective是和cnn_objective和roberta_objextive的和. 这个函数代表了在满足约束条件的前提下, 我们希望最大化的总奖励
约束条件的设定
constraints = []
for i in range(n):constraints.append(cp.sum(x[i*m: i*m+m]) == 1)
约束定义: 对于每个句子 (共n个), 添加一个约束条件, 确保每个句子只能选择一个发言人. 具体实现为:
- 初始化约束李彪: 创建一个空列表
constraints, 用于存储所有的约束条件 - 循环添加约束: 对于每个句子
for i in range(n), 执行以下操作:x[i*m: i*m+m]: 是对决策变量x的一个切片操作, 选取与第i个句子相关的部分. 由于x是一个一维数组, 这个切片实际上选取了第i. 即每个句子只能选择一个发言人
- 添加到约束列表: 将每个句子的约束条件添加到
constraints列表中
CVXPY 和 Gurobi 求解
CVXPY
CVXPY 是 Python 的一个库, 用于构建和求解凸优化问题. 在多模态发言人识别的求解器中, CVXPY 被用来定义二次规划问题. 包括构建目标函数 (RNN 输出 + Roberta 输出), 以及定义约束条件 (一个发言人).
Gurobi
Gurobi 是一个强大的数学优化求解器, 广泛应用于工业和学术界和学术界. Gurobi 能够高效的求解各种类型的优化问题. 包括线性规划, 整数规划, 二次规划等. 在我们的 Solver 中, Gurobi 被用作 CVXPY 的后端求解器. 一单优化问题在 CVXPY 中被定义, Gurobi 就被用来实际求解这个问题, 找到最优解.

CVXPY 和 Gurobi 求解优化问题
定义决策变量:
x = cp.Variable(np.prod(cnn_scores.shape), boolean=True)构建目标函数和约束:
- 上面说过了
创建优化问题:
problem = cp.Problem(cp.Maximize(objective), constraints)
求解优化问题:
problem.solve(solver='GUROBI')
处理求解结果:
return x.value.reshape(n, m), problem.status
Citation
Beasley, J. E. (1998). Heuristic algorithms for the unconstrained binary quadratic programming problem. ResearchGate. Retrieved from https://www.researchgate.net/publication/2661228
Vanderbei, R. J. (1999). LOQO: An interior point code for quadratic programming. Optimization Methods and Software, 11(1-4), 451-484. https://doi.org/10.1080/10556789908805759
Axehill, D. (2008). Integer quadratic programming for control and communication. DIVA. Retrieved from https://www.diva-portal.org/smash/record.jsf?pid=diva2:17358
相关文章:

【CCF BDCI 2023】多模态多方对话场景下的发言人识别 Baseline 0.71 Slover 部分
【CCF BDCI 2023】多模态多方对话场景下的发言人识别 Baseline 0.71 Slover 部分 概述Solver 在多模态发言人识别中的作用Solver 在多模态发言人识别中的重要性Solver 的工作原理 二次规划二次规划的基本形式二次规划的特点二次规划在多模态发言中的应用 (我的理解) 代码详解数…...

爬虫工作量由小到大的思维转变---<第十二章 Scrapy之sql存储与爬虫高效性的平衡艺术>
前言: (本文仅属于技术性探讨,不属于教文) 刚好,前阵子团队还在闲聊这个问题呢。你知道吗,在数据收集这个行当里,怎么存数据这问题就跟“先有鸡还是先有蓝”一样,没完没了的循环往复。老规矩,咱们先搞清楚我们的“鸡…...
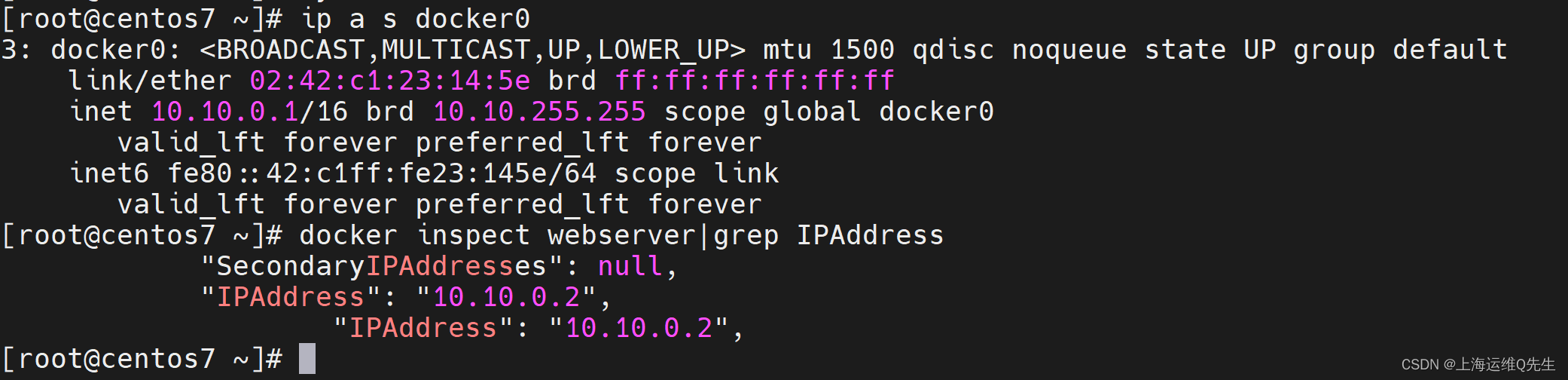
修改Docker0和容器的地址
修改Docker0和容器的地址 1. 需求 默认服务器安装完Docker-ce后会给docker0分配172.17.0.1/16地址. 公司新接入一个网段正好与172.17.0.1/16冲突,此时访问这台服务器的容器时就会发生网络不可达. 2. 解决方法 修改/etc/docker/daemon.json 加入一个自定义网段 vim /etc/d…...
弹性网络优化算法
3.3、Elastic-Net算法使用 这是scikit-learn官网给出的弹性网络回归的,损失函数公式,注意,它用的矩阵表示,里面用到范数运算。 min w 1 2 n samples ∣ ∣ X w − y ∣ ∣ 2 2 α ρ ∣ ∣ w ∣ ∣ 1 α ( 1 − ρ ) 2 ∣ ∣…...

[C语言]大小端及整形输出问题
假设在一个32位little endian 的机器上运行下面的程序,结果是多少 ? 1.1先看以下三个程序 #include <stdio.h> int main() {long long a 1, b 2, c 3;printf("%lld %lld %lld\n", a, b, c); // 1 2 3printf("%d %d %d %d %d %d\n&quo…...

C# 命令行参数解析库示例
写在前面 在日常开发中,我们经常会用到命令行参数,比如cmd下的各种指令;还有C#的控制台类型的项目,在默认入口Main函数中,那个args参数,就是有系统传入到程序进程的命令行参数;在传入的参数相对…...

2020 年网络安全应急响应分析报告
2020 年全年奇安信集团安服团队共参与和处置了全国范围内 660起网络安全应急响应事件。2020 年全年应急响应处置事件行业 TOP3 分别为:政府部门行业(146 起)医疗卫生行业(90 起)以及事业单位(61 起,事件处置数分别占应急处置所有行业的 22.1%、13.6%、9.2%。2020 年…...
Git----学习Git第一步基于 Windows 10 系统和 CentOS7 系统安装 Git
查看原文 文章目录 基于 Windows 10 系统安装 Git 客户端基于 CentOS7 系统安装部署 Git 基于 Windows 10 系统安装 Git 客户端 (1)打开 git官网 ,点击【windows】 (2)根据自己的电脑选择安装,目前一般w…...
爬虫 scrapy ——scrapy shell调试及下载当当网数据(十一)
目录 一、scrapy shell 1.什么是scrapy shell? 2.安装 ipython 3.使用scrapy shell 二、当当网案例 1.在items.py中定义数据结构 2.在dang.py中解析数据 3.使用pipeline保存 4.多条管道的使用 5.多页下载 参考 一、scrapy shell 1.什么是scrapy shell&am…...
Linux驱动(中断、异步通知):红外对射,并在Qt StatusBus使用指示灯进行显示
本文工作: 1、Linux驱动与应用程序编写:使用了设备树、中断、异步通知知识点,实现了红外对射状态的异步信息提醒。 2、QT程序编写:自定义了一个“文本指示灯”类,并放置在QMainWidget的StatusBus中。 3、C与C混合编程与…...
echarts地图的常见用法:基本使用、区域颜色分级、水波动画、区域轮播、给地图添加背景图片和图标、3d地图、飞线图
前言 最近几天用echarts做中国地图,就把以前写的demo:在vue中实现中国地图 拿来用,结果到项目里直接报错了,后来发现是因为版本的问题,没办法只能从头进行踩坑了。以下内容基于vue3 和 echarts 5.32 基本使用 获取地…...

进程间通讯-管道
介绍 管道(Pipe)是操作系统提供的一种进程间通信(IPC,Inter-Process Communication)机制,它允许一个进程的输出直接作为另一个进程的输入。管道主要分为以下两种类型: 无名管道(Unn…...
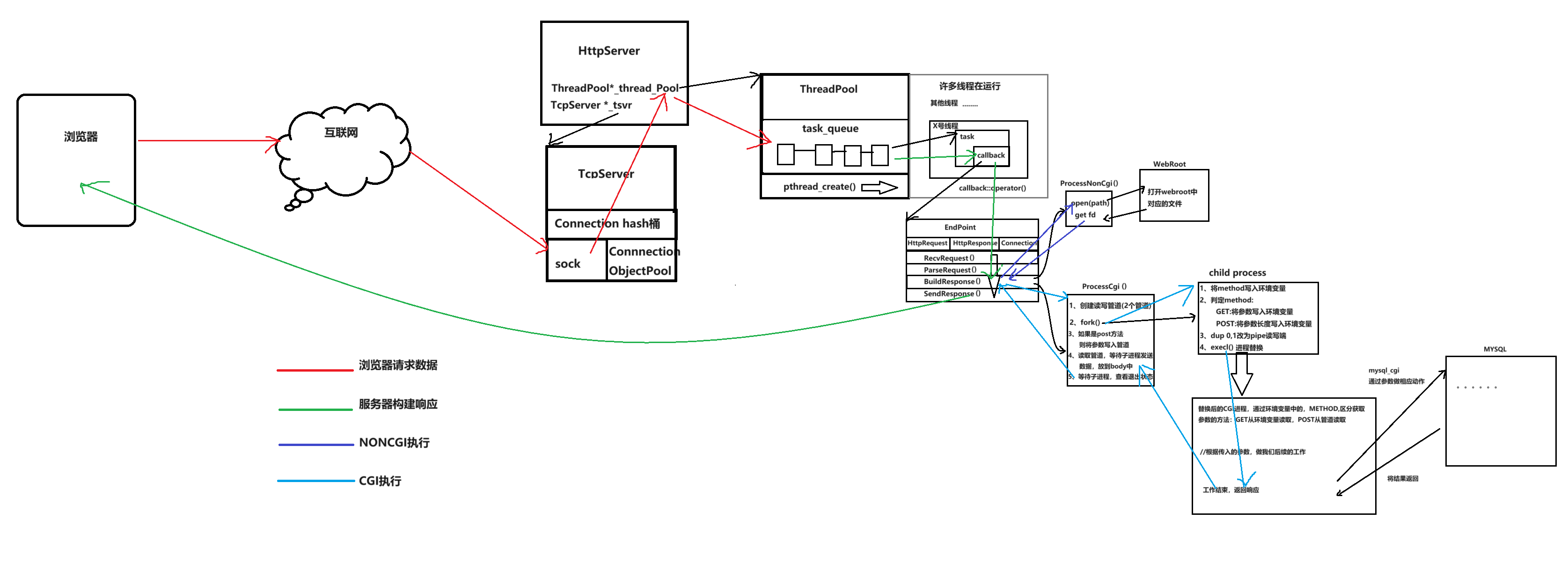
项目总结-自主HTTP实现
终于是写完了,花费了2周时间,一点一点看,还没有扩展,但是基本功能是已经实现了。利用的是Tcp为网络链接,在其上面又写了http的壳。没有使用epoll,多路转接难度比较高,以后有机会再写,…...

Java语言+二维数组+非递归实现五子棋游戏
以前做过一个C语言版五子棋:C语言+二维数组+非递归实现五子棋游戏 现在做一个Java语言版五子棋,规则如下: 1、白子为O; 2、黑子为; 3、白子先手;…...

WordCloud—— 词云
【说明】文章内容来自《机器学习入门——基于sklearn》,用于学习记录。若有争议联系删除。 wordcloud 是python的第三方库,称为词云,也成文字云,可以根据文本中的词频以直观和艺术化的形式展示文本中词语的重要性。 依赖于pillow …...

linux网络----UDP编程
一、函数接口: 1.socket:创建一个用来网络通信的终端节点; 参数: type:套接字类型 SOCK_STREAM 流式套接字 TCP SOCK_DGRAM 数据报套接字 UDP SOCK_RAM 原始套接字 domain: 协议族 AF_INET protocal: 默认为0 2.s…...

[AI工具推荐]AiRestful智能API代码生成
智能API代码示例生成工具AiRestful 一、产品介绍二、如何使用1、第一步(必须):2、第二步(可选):3、第三步(智能生成): 三、如何集成到您的网站(应用)1、开始接入2、接入案例 四、注意点 一、产品介绍 AiRestful是一款基于智能AI的,帮助小白快速生成任意编程语言的API接口调用示…...

Elasticsearch 8.10.0同义词API用法详解,支持同义词热更新
Elasticsearch 的同义词功能非常强大,如果使用得当,可以显着提高搜索引擎的效果。使用同义词功能时的一个常见问题是更新同义词集。 同义词在搜索引擎领域用途 同义词在搜索引擎领域的用途可概括如下: 增强搜索的准确性——当用户输入一个关键词时,可能与他们实际意图相关…...

深度学习之模型权重
在深度学习中,模型的权重(weights)是指神经网络中的参数,这些参数用于调整和学习模型的行为,以便能够对输入数据进行有效的映射和提取有用的特征。深度学习模型通常由许多神经元和连接组成,而权重就是连接这…...
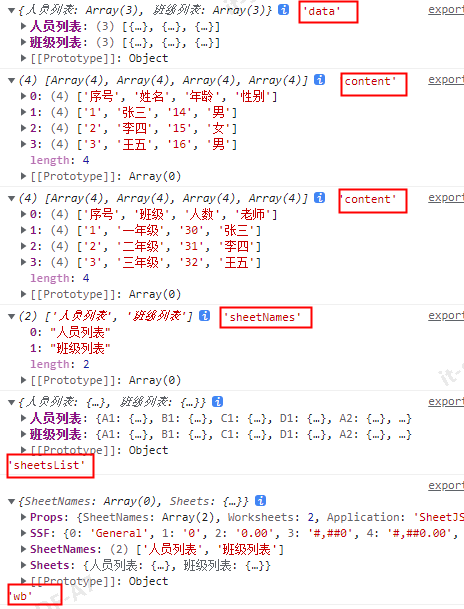
纯前端使用XLSX导出excel表格
1 单个sheet page.js(页面中的导出方法) import { exportExcel } from ../../../utils/exportExcel.js; leadOut() {const arr [{ id: 1, name: 张三, age: 14, sex: 男 },{ id: 2, name: 李四, age: 15, sex: 女 },{ id: 3, name: 王五, age: 16, sex: 男 },];const allR…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...
