实验三、数字PID控制器的设计
实验三、数字PID控制器的设计
--- 直流闭环调速实验
一、实验目的
1.理解晶闸管直流单闭环调速系统的数学模型和工作原理;.
2. 掌握PID控制器参数对控制系统性能的影响;
3. 能够运用MATLAB/Simulink软件对控制系统进行正确建模并对模块进行正确的参数设置;
4. 掌握计算机控制仿真结果的分析方法。
二、实验工具
MATLAB 软件( 2022a);
三、实验要求
1、独立编写数字PID控制器仿真程序,并根据实验曲线,进行仿真结果分析。
2、在进行数字PID控制作用分析时,建议采用如下两种方法:
a.先求出整个闭环系统传递函数,采用Matlab中的c2d函数指令对其进行离散化,分析Kp, Ta, Ta选用不同参数时对系统稳定性和动态特性的影响。
b.分别对PID控制器和被控对象进行离散化。其中:
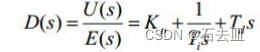
那么:
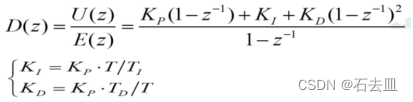
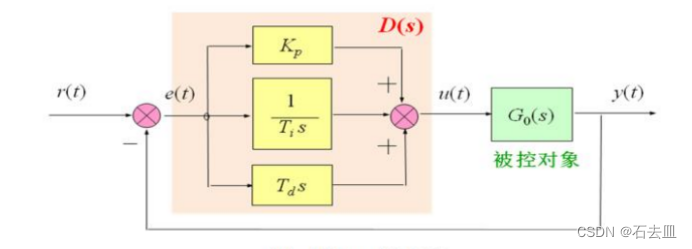
模拟PID控制系统
c.讨论PID参数整定和Ts选取的意义。
四、实验内容
已知晶闸管直流单闭环调速系统的转速控制器为PID控制器,如图所示。试运用MATLAB软件对调速系统的P、I、 D控制作用进行分析。
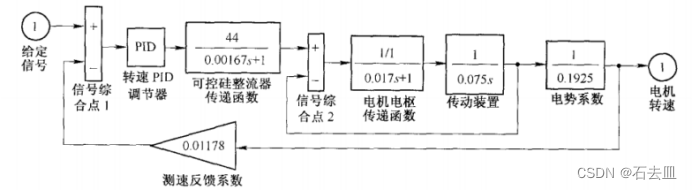
单闭环调速系统
五、实验步骤
(一)模拟PID控制作用分析:
运用MATLAB软件对调速系统的P、I、D控制作用进行分析。
(1)比例控制作用分析
为分析纯比例控制的作用,考察当Tg=0, T=∞, K,=1~ 5时对系统阶跃响应的影响。
MATLAB程序如下:
- clear
- clc
- G1=tf(1,[0.017 1]);
- G2=tf(1,[0.075 0]);
- G12=feedback(G1*G2,1);
- G3=tf(44,[0.00167 1]);
- G4=tf(1,0.1925);
- G=G12*G3*G4;
- Kp=1:1:5;
- for i=1:length(Kp)
- Gc=feedback(Kp(i)*G,0.01178);
- step(Gc),hold on
- end
- axis([0 0.2 0 130]);
- gtext('1Kp=1'),
- gtext('2Kp=2'),
- gtext('3Kp=3'),
- gtext('4Kp=4'),
- gtext('5Kp=5'),
参考图如下:

P控制阶跃响应曲线
分析如下:
图为P控制阶跃响应曲线。比例调节器对偏差是即时反应的,偏差一旦出现,调节器即控制使其输出量朝着减小偏差的方向变化,控制作用的强弱取决于比例系数^p。比例调节器虽然简单快速,但对于系统响应为有限值的控制对象存在稳态误差。加大比例系数可以减小稳态误差,但过大时会使系统的动态质量变坏,引起输出量震荡,甚至导致闭环系统不稳定。
随着Kp的增加,闭环系统的超调量增加,响应速度加快,控制时间加长,稳态误差减少;但不能完全消除静态误差。随着其继续增加,系统的稳定性变差。本例中当Kp大于等于21后,系统变为不稳定。
(2)积分控制作用分析
保持Kp=1不变,考察Ti = 0.03 ~ 0.07时对系统阶跃响应的影响。MATLAB程序如下:
- G1=tf(1,[0.017 1]);
- G2=tf(1,[0.075 0]);
- G12=feedback(G1*G2,1);
- G3=tf(44,[0.00167 1]);
- G4=tf(1,0.1925);
- G=G12*G3*G4;
- Kp=1;
- Ti=0.03:0.01:0.07;
- for i=1:length(Ti)
- Gc=tf(Kp*[Ti(i) 1],[Ti(i) 0]);
- Gcc=feedback(G*Gc,0.01178);
- step(Gcc),hold on
- end
- gtext('1Ti=0.03'),
- gtext('2Ti=0.04'),
- gtext('3Ti=0.05'),
- gtext('4Ti=0.06'),
- gtext('5Ti=0.07'),
参考图如下:
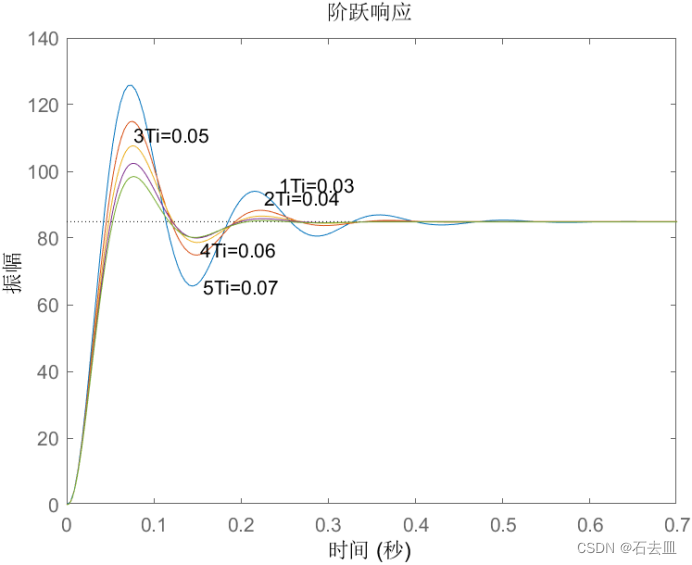
Ti控制阶跃响应曲线
分析如下:
图为PI控制阶跃响应曲线。引入积分环节可以消除在比例积分中的残余稳态误差。但当积分时间常数Ti增大,那么积分作用变弱,反之变强,因此增大Ti将减慢消除稳态误差的过程,但减小超调,提高系统的稳定性。引入积分环节的代价就是降低了系统的快速性。由图可知,随着Ti的增加,系统的超调量减小,响应速度减慢;Ti太小,系统将会变得不稳定; Ti能完全消除系统的静态误差,提高系统的控制精度。
(3)微分控制作用分析
为分析微分控制的作用,保持K。=0.01,T =0.01不变,考察当T =12 ~ 84时对系统阶跃响应
的影响。MATLAB 程序如下: .
- G1=tf(1,[0.017 1]);
- G2=tf(1,[0.075 0]);
- G12=feedback(G1*G2,1);
- G3=tf(44,[0.00167 1]);
- G4=tf(1,0.1925);
- G=G12*G3*G4;
- Kp=0.01;
- Ti=0.01;
- Td=12:36:84;
- for i=1 :length(Td)
- Gc=tf(Kp*[Ti*Td(i) Ti 1],[Ti 0]);
- Gcc=feedback(G* Gc,0.01178);
- step(Gcc),hold on
- pause(1)
- end
- gtext('1Td=12'),
- gtext('2Td=48'),
- gtext('3Td=84'),
参考图如下:
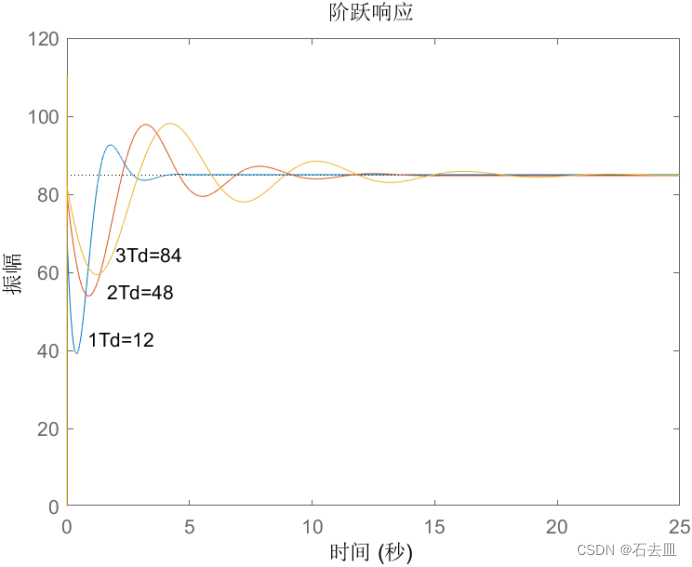
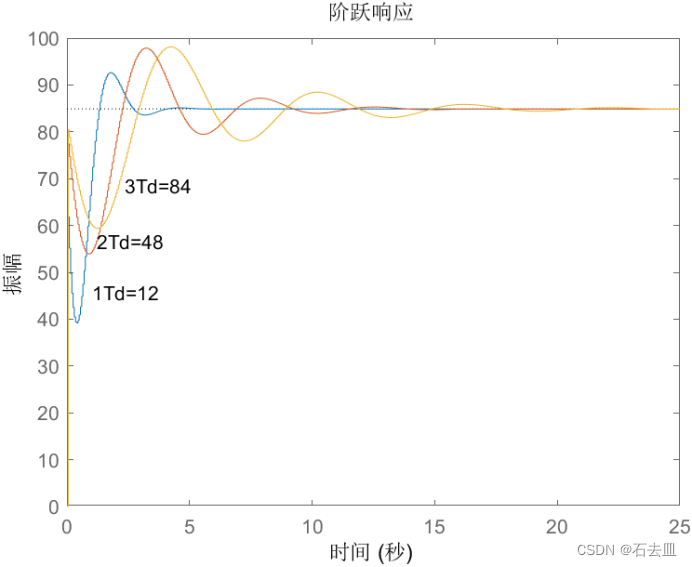
Td控制阶跃响应曲线
分析如下:
图为PD控制阶跃响应曲线。微分调节的原理是在偏差出现或出现的瞬间,按偏差变化的趋向进行控制,使偏差消失在萌芽阶段,从而达到加快控制作用的效果,引入微分环节会降低最大超调量,减少.上升时间和调节时间,使系统趋于稳定。由图可知,由于微分环节的作用,在曲线的起始上升段出现了一个尖锐的波峰,之后曲线也呈衰减的振荡:随着Td增加,系统的超调量增大,但曲线尖锐的起始上升阶段后响应速度减慢,可以看出Td越小。调节作用越好。
(二)数字PID控制作用分析:
仿照上述过程,独立完成PID离散化仿真程序编写及结果分析。
(1)比例控制作用下,取采样时间0.001 秒。
代码如下:
- clear
- clc
- G1=tf(1,[0.017 1]);
- G2=tf(1,[0.075 0]);
- G12=feedback(G1*G2,1);
- G3=tf(44,[0.00167 1]);
- G4=tf(1,0.1925);
- G=G12*G3*G4;
- Kp=1:1:5;
- ts=0.001;
- for i=1:length(Kp)
- Gc=feedback(Kp(i)*G,0.01178);
- Gcc=c2d(Gc,ts, 'zoh');
- step(Gcc),hold on
- end
- axis([0 0.2 0 130]);
- gtext('1Kp=1'),
- gtext('2Kp=2'),
- gtext('3Kp=3'),
- gtext('4Kp=4'),
- gtext('5Kp=5'),
仿真结果参考图:
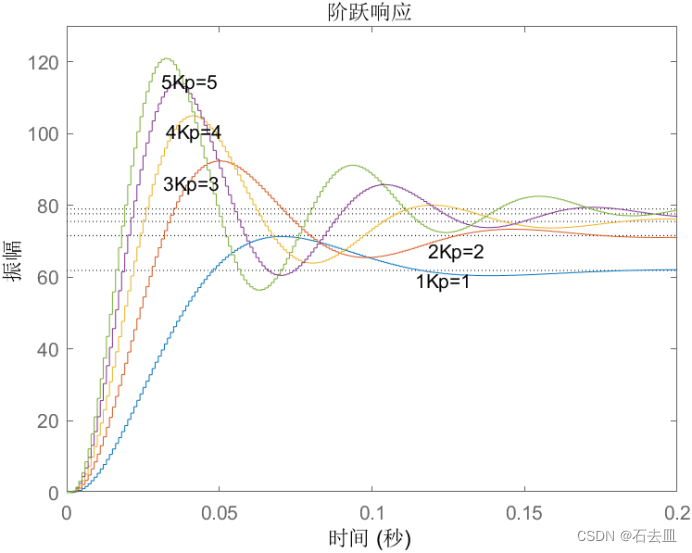
分析如下:
Kp增加,系统响应速度 加快:如果Kp偏大, 系统输出震荡次数增多,调节时间加长:Kp过大将导致系统的不稳定 。
- 比例积分控制作用下,取采样时间0.001秒。
代码如下:
- G1=tf(1,[0.017 1]);
- G2=tf(1,[0.075 0]);
- G12=feedback(G1*G2,1);
- G3=tf(44,[0.00167 1]);
- G4=tf(1,0.1925);
- G=G12*G3*G4;
- Kp=1;
- Ti=0.03:0.01:0.07;
- ts=0.001;
- for i=1:length(Ti)
- Gc=tf(Kp*[Ti(i) 1],[Ti(i) 0]);
- Gcc=feedback(G*Gc,0.01178);
- Gccd=c2d(Gcc,ts, 'zoh');
- step(Gccd),hold on
- pause(1)
- end
- gtext('1Ti=0.03'),
- gtext('2Ti=0.04'),
- gtext('3Ti=0.05'),
- gtext('4Ti=0.06'),
- gtext('5Ti=0.07'),
仿真结果参考图:
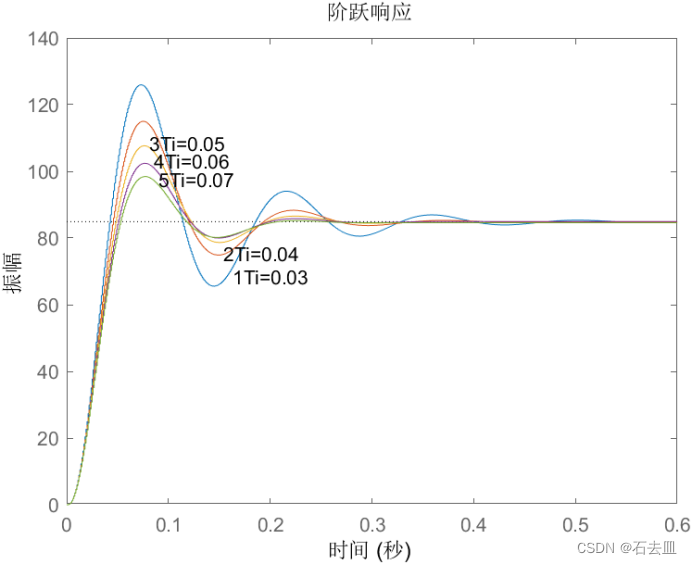
分析如下:
积分控制能消除系统静差,但若Ti太大,积分作用太弱,以致不能消除静差;若太小,系统将不稳定。
(3)比例积分微分控制作用下,取采样时间0.05秒。.
代码如下:
- G1=tf(1,[0.017 1]);
- G2=tf(1,[0.075 0]);
- G12=feedback(G1*G2,1);
- G3=tf(44,[0.00167 1]);
- G4=tf(1,0.1925);
- G=G12*G3*G4;
- Kp=0.01;
- Ti=0.01;
- Td=12:36:84;
- ts=0.05;
- for i=1 :length(Td)
- Gc=tf(Kp*[Ti*Td(i) Ti 1],[Ti 0]);
- Gcc=feedback(G* Gc,0.01178);
- Gccd=c2d(Gcc,ts, 'zoh');
- step(Gccd),hold on
- pause(1)
- end
- gtext('1Td=12'),
- gtext('2Td=48'),
- gtext('3Td=84'),
仿真结果参考图:
实验分析:
选择合适的Td将使系统的超调量减小,增加系统的稳定性,调节时间缩短,允许加大比例控制:但若过大或过小都不会达到效果。
六、实验总结
1、模拟PID控制:
在模拟PID控制器中,比例环节的作用是对偏差瞬间作出反应。偏差一旦产生,控制器立即产生控制作用,使控制量向减小偏差的方向变化。控制作用的强弱取决于比例系数Kp。Kp越大,控制作用越强,则过渡过程越快,控制过程的静态偏差也就越小。但是Kp越大,也越容易产生振荡,破坏系统的稳定性。积分环节虽然会消除静态误差,但是也会降低系统的响应速度,增加系统的超调量。积分时间常数越大,积分的积累越弱。这时,系统在过渡时不会产生振荡。但是,增大积分时间常数会减慢静态误差的消除过程,消除偏差所需的时间也较长,但可以减少超调量,提高系统的稳定性。当积分时间常数较小时,则积分的作用较强。这时系统过渡时间中有可能产生振荡,不过消除偏差所需的时间较短。所以必须根据实际控制的具体要求来确定积分时间常数。微分环节的作用是阻止偏差的变化。它根据偏差的变化趋势(变化速度)进行控制。偏差变化的越快,微分控制器的输出就越大,并能在偏差值变大之前进行修正。微分作用的引入,有助于减小超调量、克服振荡,使系统趋于稳定。特别对高阶系统有利,它加快了系统的跟踪速度。但微分的作用对输入信号的噪声很敏感。对那些噪声较大的系统一-般不用微分,或在微分起作用之前先对输入信号进行滤波。微分部分的作用由微分时间常数决定。微分时间常数越大时,则它抑制偏差变化的作用越强;微分时间常数越小时,则它反抗偏差变化的作用越弱。微分部分显然对系统稳定有很大的作用。适当地选择微分时间常数,可以使微分作用达到最优。
2、数字PID控制:
因为在微机处理器里面是通过软件来实现PID控制算法的,所以必须将模拟PID控制器进行离散化处理,这样控制器只需根据采样时刻的偏差值计算控制量。控制器成比例的反映控制系统的误差信号,偏差一旦产生,控制器立即产生控制作用,以减小偏差。比例控制器在信号变换时,只改变信号的幅值而不改变信号的相位,采用比例控制可以提高系统的开环增益,是系统的主要控制部分。积分控制主要用于消除静差,提高系统的无差度,但是会使系统的震荡加剧,超调增大,损害动态性能,一般不单独作用,而是与PD控制相结合。积分作用的强弱取决于积分时间常数Ti,时间常数越大,积分作用就越弱,反之则越强。
4、采样周期:
对于Ts,采样周期Ts越小,数字模拟越精确,控制效果越接近连续控制。对大多数算法,缩短采样周期可使控制回路性能改善,但采样周期缩短时,频繁的采样必然会占用较多的计算工作时间,同时也会增加计算机的计算负担,而对有些变化缓慢的受控对象无需很高的采样频率即可满意地进行跟踪,过多的采样反而没有多少实际意义。
其中选择采样周期应综合考虑的因素:
第一,给定值的变化频率。加到被控对象上的给定值变化频率越高,采样频率应越高,以使给定值的改变通过采样迅速得到反映,而不致在随动控制中产生大的时延。
第二,被控对象的特性。考虑对象变化的缓急,若对象是慢速的热工或化工对象时,T一般取得较大。在对象变化较快的场合,T应取得较小。考虑干扰的情况,从系统抗干扰的性能要求来看,要求采样周期短,使扰动能迅速得到校正。
第三,使用的算式和执行机构的类型。采样周期太小,会使积分作用、微分作用不明显。同时,因受微机计算精度的影响,当采样周期小到一定程度时,前后两次采样的差别反映不出来,使调节作用因此而减弱。执行机构的动作惯性大,采样周期的选择要与之适应,否则执行机构来不及反应数字控制器输出值的变化。
第四,控制的回路数。要求控制的回路较多时,相应的采样周期越长,以使每个回路的调节算法都有足够的时间来完成。
- 总结:
本次实验是对PID算法以及MATLAB应用的初步掌握,经过本次实验,我对PID算法有了进一步的认识。期间遇到过许多上述提到过的类似问题,虽然这些问题看似简单,但如若不亲自经历并寻求方法解决,下次遇到可能仍然不会解决。此外,通过此次课程设计,我也明白了自学能力的重要性,在今后的学习中,我们仍会遇到各种难题,这些都需要我们通过自学逐渐解决。最后,课程设计的结果固然重要,但是我认为这个过程才是更重要的,过程中培养的能力、掌握的经验会让我们受益终身。
相关文章:

实验三、数字PID控制器的设计
实验三、数字PID控制器的设计 --- 直流闭环调速实验 一、实验目的 1.理解晶闸管直流单闭环调速系统的数学模型和工作原理;. 2. 掌握PID控制器参数对控制系统性能的影响; 3. 能够运用MATLAB/Simulink软件对控制系统进行正确建模并对模块进行正确的参数设置; 4.…...
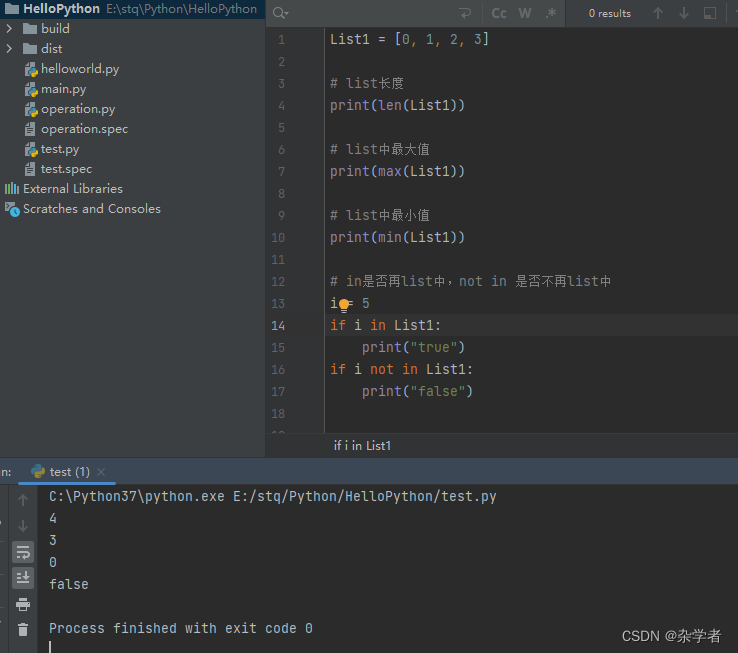
python List和常用的方法
List:列表中包含多个数据,数据之间使用逗号分隔,索引从0开始。 空列表: dir:查看列表的所有方法 List常用方法:insert、append,extend、del、remove、pop、clear、count、index 增加insert(索引…...

PMP证书要怎么考,含金量怎么样?
对于新改版的PMP提纲,很多人都不知道如何去备考,这里我就总结一些经验,希望能帮助到大家!! 一,学习内容及考试形式? 学习内容:《PMBOK》项目管理知识体系指南,建议大家…...
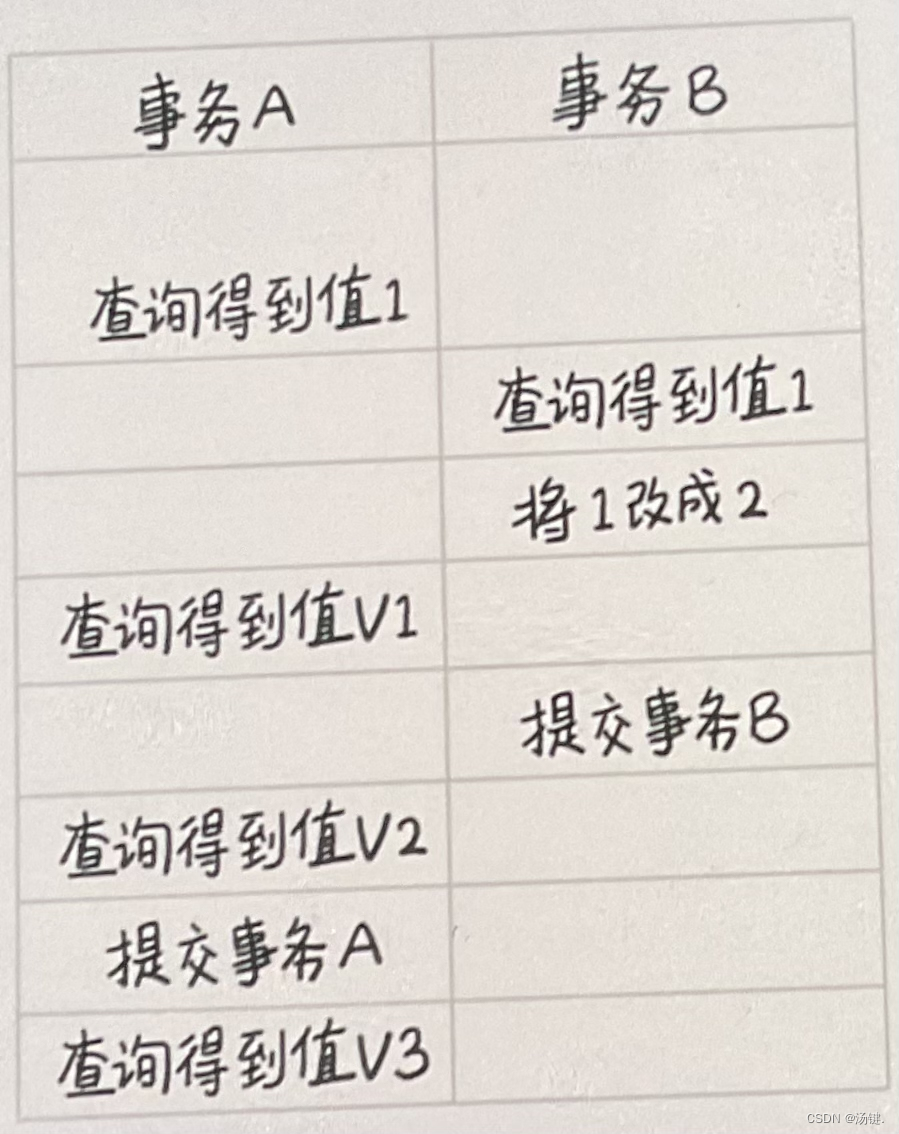
MySQL实战解析底层---事务隔离:为什么你改了我还看不见
目录 前言 隔离性与隔离级别 事务隔离的实现 事务的启动方式 前言 和数据库打交道的时候,总是会用到事务最经典的例子就是转账,你要给朋友小王转 100 块钱,而此时你的银行卡只有 100 块钱转账过程具体到程序里会有一系列的操作࿰…...
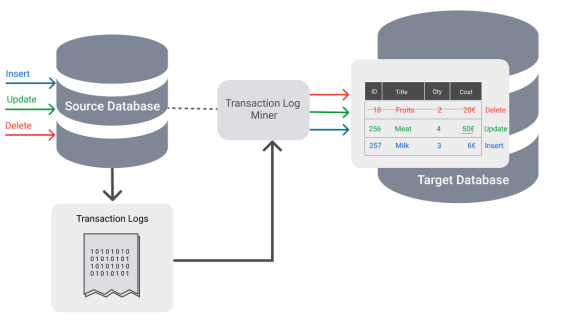
变更数据捕获(CDC)
从广泛意义上说,全球许多企业每天都需要通过频繁的数据批量处理与加载,来定期将数据从一个数据库迁移到另一个数据库(或数据仓库)。这类定期批量加载的工作,往往既耗费时间,又会消耗原始系统的大量处理能力。因此,管理…...
【移动端表格组件】uniapp简单实现H5,小程序,APP多端兼容表格功能,复制即用,简单易懂【详细注释版本】
前言: 由于最近需要做移动端的项目 有个pc端的后台系统里面需要移一部分页面过来 而里面就有很多的表格,我就开始惯例网上先找前人栽的树,我好乘凉 然后找了一圈发现,不管是主流的移动端ui库或者网上自己写的帖子,或者…...
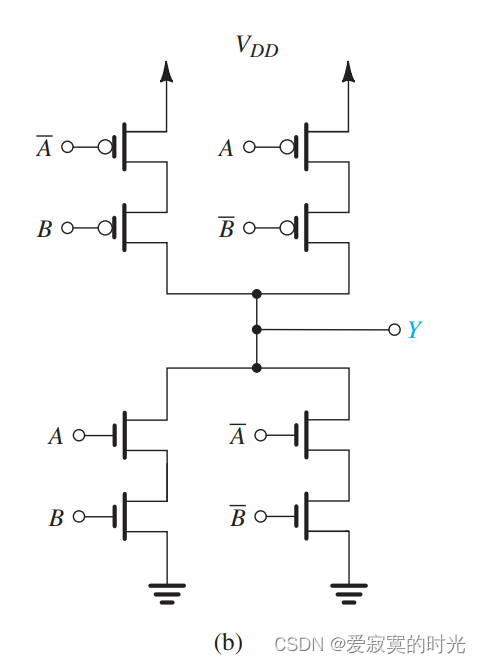
电子技术——CMOS 逻辑门电路
电子技术——CMOS 逻辑门电路 在本节我们介绍如何使用CMOS电路实现组合逻辑函数。在组合电路中,电路是瞬时发生的,也就是电路的输出之和当前的输入有关,并且电路是无记忆的也没有反馈。组合电路被大量的使用在当今的数字逻辑系统中。 晶体管…...

【C++】C++11 新特性
目录 1.列表初始化 1.1. C98中使用{}初始化的问题 1.2. 内置类型的列表初始化 1.3. 自定义类型的列表初始化 2. 变量类型推导 2.1. 为什么需要类型推导 2.2. decltype类型推导 2.2.1 为什么需要decltype 2.2.2. decltype 3. 对默认成员的控制(default、delete) 3.1. …...

JPA 相关注解说明
jpa相关注解 JPA(Java Persistence API)是一种Java规范,定义了一套标准的对象关系映射(ORM)API,用于将Java对象映射到关系型数据库中。JPA旨在统一各种ORM框架之间的差异,提供一种标准化的ORM解…...

SAP 生产订单/流程订单中日期的解释
SAP 生产订单/流程订单中日期的解释 基本开始日期:表示订单的开始日期 基本完成日期:表示订单的完成日期 我们在输入基本开始日期和基本完成日期时需要关注 调度 下面的“类型”,其中有向前、向后、当天日期等: 调度类型 为向前…...
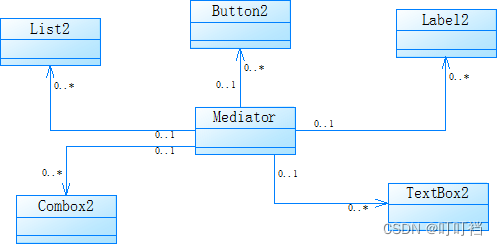
Java设计模式笔记——七大设计原则
系列文章目录 第一章 Java 设计模式之七大设计原则 文章目录系列文章目录前言一、单一职责原则1.案例分析2.改进二、开闭原则1.案例分析2.改进三、里氏替换原则1.案例分析2.改进四、依赖倒转原则五、接口隔离原则1.案例分析2.改进六、合成复用原则1.案例分析2.改进七、迪米特原…...
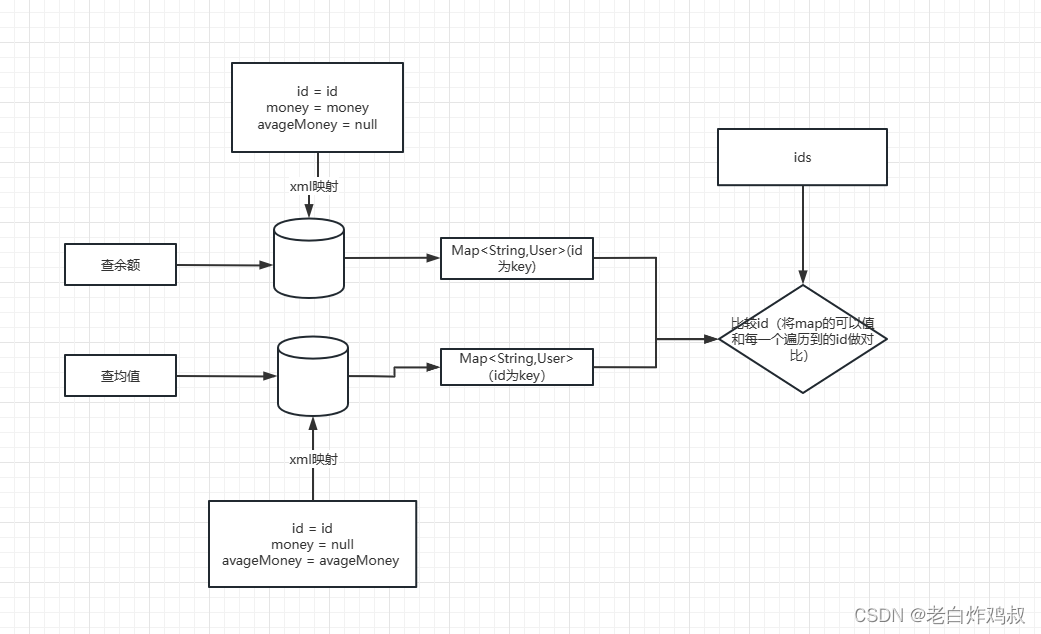
记录第一次接口上线过程
新入职一家公司后,前三天一直在学习公司内部各种制度文化以及考试。 一直到第三天组长突然叫我过去,给了一个需求的思维导图,按照这个需求写这样一个接口, 其实还不错,不用自己去分析需求,按照这上面直接开…...

时序预测 | MATLAB实现Rmsprop算法优化LSTM长短期记忆神经网络时间序列多步预测(滚动预测未来,多指标,含验证Loss曲线)
时序预测 | MATLAB实现Rmsprop算法优化LSTM长短期记忆神经网络时间序列多步预测(滚动预测未来,多指标,含训练和验证Loss曲线) 目录 时序预测 | MATLAB实现Rmsprop算法优化LSTM长短期记忆神经网络时间序列多步预测(滚动预测未来,多指标,含训练和验证Loss曲线)效果一览基本描…...

如何利用Level2行情数据接口追板和交易股票?
十档行情看得更深的A股行情软件,我们在盘口数据中可以看到,买一到买五以及卖一到卖五,共10个价位的挂单情况,但基于上证所的level-2行情软件,视野则扩展到了买一到买十以及卖一到卖十数据,无疑比所有免费软…...

MySQL常用的聚合函数
聚合函数聚合函数对一组值进行运算,并返回单个值。也叫组合函数函数作用COUNT(*|列名) 统计查询结果的⾏数AVG(数值类型列名)求平均值,返回指定列数据的平均值SUM (数值类型列名)求和,返回指定列的总和MAX(列名)查询指定列的最⼤值MIN(列名)查…...
如何评估模糊测试工具-unibench的使用
unibench是一个用来评估模糊测试工具的benchmark。这个benchmark集成了20多个常用的测试程序,以及许多模糊测试工具。 这篇文章(https://zhuanlan.zhihu.com/p/421124258)对unibench进行了简单的介绍,本文就不再赘诉,…...

2023初级会计详细学习计划打卡表!自律逆袭,一次上岸!
2023年初级会计职称考试报名时间:2月7日-28日考试时间:5月13日—17日给大家整理了《经济法基础》和《初级会计实务》两科超实用的学习打卡表重要程度、难易度、易错点、要求掌握内容、章节估分等都全部总结在一起,一目了然!为什么…...

【Python】Python项目打包发布(四)(基于Nuitka打包PySide6项目)
Python项目打包发布汇总 【Python】Python项目打包发布(一)(基于Pyinstaller打包多目录项目) 【Python】Python项目打包发布(二)(基于Pyinstaller打包PyWebIO项目) 【Python】Pytho…...
)
一起Talk Android吧(第五百一十三回:Java中的byte数组与int变量相互转换)
文章目录整体思路示例代码各位看官们大家好,上一回中咱们说的例子是"自定义Dialog",这一回中咱们说的例子是" Java中的byte数组与int变量相互转换"。闲话休提,言归正转, 让我们一起Talk Android吧!在实际项目…...
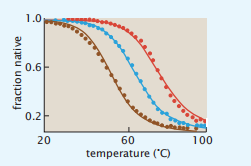
22《Protein Actions Principles and Modeling》-《蛋白质作用原理和建模》中文分享
《Protein Actions Principles and Modeling》-《蛋白质作用原理和建模》 本人能力有限,如果错误欢迎批评指正。 第五章:Folding and Aggregation Are Cooperative Transitions (折叠和聚合是同时进行的) -蛋白质折叠的协同作…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...
