大数据机器学习深度解读决策树算法:技术全解与案例实战
大数据机器学习深度解读决策树算法:技术全解与案例实战
本文深入探讨了机器学习中的决策树算法,从基础概念到高级研究进展,再到实战案例应用,全面解析了决策树的理论及其在现实世界问题中的实际效能。通过技术细节和案例实践,揭示了决策树在提供可解释预测中的独特价值。
一、引言
决策树算法是机器学习领域的基石之一,其强大的数据分割能力让它在各种预测和分类问题中扮演着重要的角色。从它的名字便能窥见其工作原理的直观性:就像一棵树一样,从根到叶子的每一分叉都是一个决策节点,指引数据点最终归类到相应的叶节点,或者说是最终的决策结果。
在现实世界中,决策树的概念可以追溯到简单而普遍的决策过程。例如,医生在诊断病人时,会根据一系列的检查结果来逐步缩小疾病的范围,这个过程可以被视作一种决策树的实际应用。从症状到测试,每一个节点都是决策点,携带着是否进一步检查或是得出诊断的决策。
在机器学习的世界里,这种决策过程被数学化和算法化。我们不再是用肉眼观察,而是让计算机通过算法模拟这一过程。举个例子,电子邮件过滤器就是决策树应用的一个经典案例。它通过学习识别垃圾邮件和非垃圾邮件的特征,比如关键词的出现频率、发件人信誉等,电子邮件过滤器能够自动地将邮件分类为“垃圾邮件”或“正常邮件”。
在更广泛的机器学习应用领域,决策树可以处理各种各样的数据,不论是数字还是分类数据,它都能以其独到的方式进行分析。例如,在金融领域,决策树能够帮助评估和预测贷款违约的可能性;在电子商务中,它可以用来预测用户的购买行为,甚至在更复杂的领域,比如生物信息学中,决策树可以辅助从复杂的基因数据中发现疾病与特定基因之间的关联。
通过引入机器学习,我们让决策树这一概念超越了人类直觉的局限性,使它能处理远超人脑处理能力的数据量和复杂度。它们不仅能够基于现有数据做出判断,还能从数据中学习,不断优化自身的决策规则,这是决策树在现实世界中不可替代的意义。
决策树之所以在机器学习中占有一席之地,还因为它的模型可解释性强,这在需要透明决策过程的领域尤为重要。与深度学习的黑盒模型相比,决策树提供的决策路径是清晰可追踪的。每一次分支都基于数据特征的显著性进行选择,这让非专业人士也能够理解模型的决策逻辑。
在本文中,我们将深入探讨决策树的核心技术,从它的数学基础到如何优化算法以处理各类数据挑战,再到通过实际案例展示它们如何解决现实世界的问题。我们将走进决策树的世界,了解这一技术如何在机器学习的众多领域中发挥着它的重要作用。
二、决策树基础
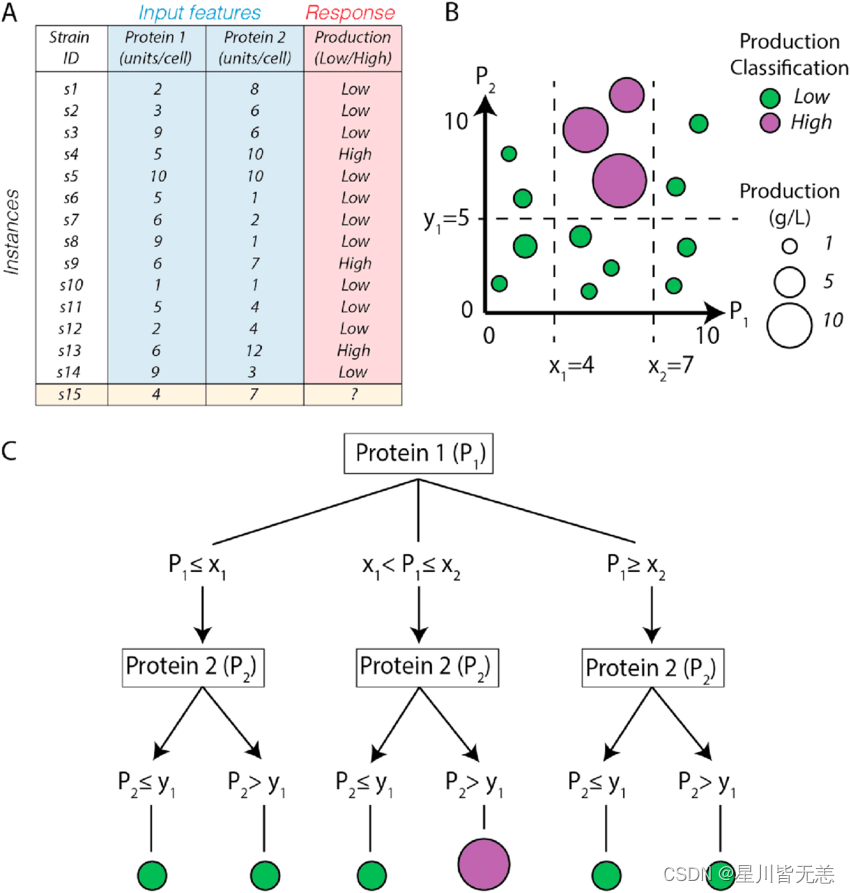
决策树,作为一种符号学习方法,将复杂的决策规则转化为一系列简单的比较问题,从而对数据进行分类或回归。它们通过递归分裂训练数据集,构建一个树状的模型。
决策树模型概述
在决策树中,每个内部节点代表一个特征上的测试,每个分支代表测试的结果,而每个叶节点代表最终的决策结果。决策树的构建始于根节点,包含整个训练集,通过分裂成子节点的过程,逐渐学习数据中的规律。
想象一下,我们面前有一篮水果,目的是区分苹果和橘子。一棵决策树可能首先询问:“这个水果的颜色是红色吗?”如果答案是肯定的,它可能会将这个水果分类为苹果;否则,它会继续询问:“这个水果的质感是光滑的吗?”这样的一系列问题最终导致分类的结果,这就是决策树的工作方式。
构建决策树的关键概念
特征选择
决策树如何确定在每个节点上提出哪个问题?这就涉及到一个关键的概念——特征选择。特征选择是决定用哪个特征来分裂节点的过程,它对决策树的性能有着至关重要的影响。主要的特征选择方法包括:
信息增益:度量分裂前后信息不确定性的减少,也就是说,它寻找能够最好地清理数据的特征。
增益率:调整信息增益,解决偏向于选择拥有大量值的特征的问题。
基尼不纯度:常用于CART算法,度量数据集的不纯度,基尼不纯度越小,数据集的纯度越高。
假设我们要从一个包含苹果和橘子的篮子中分类水果,信息增益会衡量按照颜色或按照质地分裂数据所带来的信息纯度提升。如果颜色的信息增益更高,那么颜色就是该节点的最佳分裂特征。
决策树的生成
树的生成是通过递归分裂的方式进行的。从根节点开始,使用特征选择方法选择最佳的分裂特征,创建分支,直到满足某个停止条件,比如达到了设定的最大深度,或者节点中的样本数量少于阈值。
举一个现实生活中的例子,假如一个电信公司想要预测哪些客户可能会流失。在构建决策树时,它可能会首先考虑账单金额,如果账单金额大于平均值,那么进一步考虑客户的合同期限;如果合同期限短,那么客户流失的可能性就更高。
决策树的剪枝
为了防止过拟合——即模型对训练数据过于敏感,从而无法泛化到新的数据上——决策树需要进行剪枝。剪枝可以理解为对树
进行简化的过程,包括预剪枝和后剪枝。预剪枝意味着在树完全生成之前停止树的生长;后剪枝则是在树生成之后去掉某些分支。
例如,在预测客户流失的决策树中,如果我们发现分裂后每个节点只包含极少量的客户,那么这可能是一个过拟合的信号。通过预剪枝或后剪枝,我们可以移除这些仅对训练数据有特定判断能力的规则。
决策树的基础原理既直观又深邃。它将复杂的决策过程简化为易于理解的规则,并且通过学习数据中固有的模式,适用于各种机器学习任务。
三、算法研究进阶
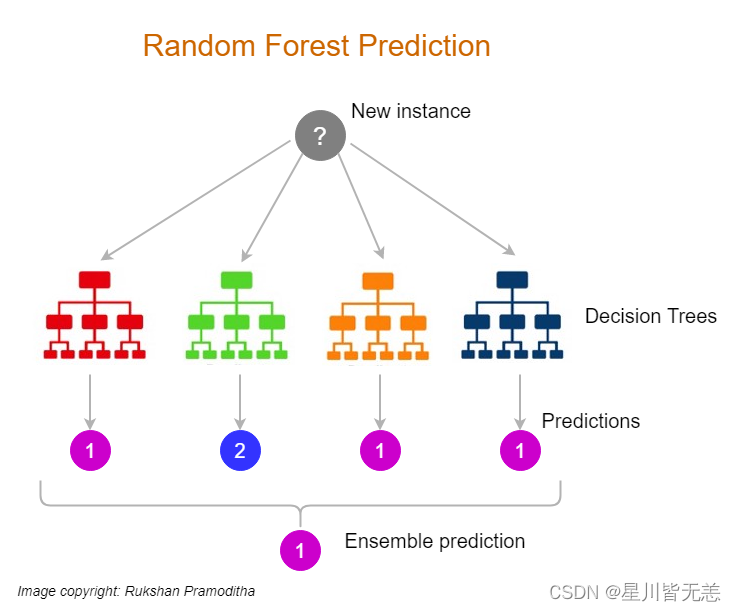
进入到算法研究的进阶阶段,我们将探讨决策树的深层次技术演进和最新研究成果,以及如何将这些先进的理念应用于解决更复杂的问题。
提升树和随机森林
决策树的强大之处不仅在于它们单独的决策能力,而且还在于它们可以组合成更强大的模型,如提升树(Boosted Trees)和随机森林(Random Forests)。
提升树(Boosted Trees)
提升树是通过结合多个弱决策树构建的,每一棵树都试图纠正前一棵树的错误。使用梯度提升(Gradient Boosting)的方法可以系统地将新模型添加到已经存在的模型集合中,从而逐步提升模型的准确率。
以预测房价为例,我们可能首先使用一个简单的决策树来预测价格,然后第二棵树会专注于第一棵树预测错误的部分,通过减少这些错误来提升模型的性能,直到达到一定的准确率或树的数量。
随机森林(Random Forests)
随机森林通过创建多个独立的决策树,并让它们对最终结果进行投票,来提高决策树的准确性和鲁棒性。每一棵树都是在数据集的一个随机子集上训练得到的,这种方法即提高了模型的泛化能力,也增加了结果的稳定性。
设想一个信用评分的场景,单一决策树可能会因为训练数据中的随机波动或噪声而产生过度特定的规则。而随机森林通过集成多个树的决策来平均这些波动,生成更为稳定和可靠的信用评分。
进化算法与决策树
研究人员还在探索如何使用进化算法(Evolutionary Algorithms)来优化决策树的结构和参数。进化算法模拟生物进化的过程,通过选择、交叉和变异操作来优化问题的解。
决策树结构的进化
在实践中,可能会将决策树的每一部分——分裂规则、特征选择、甚至是剪枝策略——看作是个体的基因。通过定义适应度函数来评估树的性能,进化算法会不断迭代,选择出性能最佳的树进行繁衍,从而得到更加优化的决策树结构。
例如,在电子商务推荐系统中,我们可以利用进化算法来不断进化决策树的结构,以提高推荐的准确性。不同的树结构被视为不同的“物种”,经过迭代的“自然选择”,最适应用户行为模式的决策树结构会被保留下来。
多目标决策树优化
在某些复杂的机器学习任务中,我们不仅仅想要优化单一的性能指标,如准确度,我们还可能关心模型的可解释性、速
度或是占用的内存大小。多目标优化(Multi-Objective Optimization)技术能够在这些不同的指标之间找到最佳的平衡。
应用实例:财务风险评估
在财务风险评估中,我们需要一个既准确又快速的模型来实时分析交易的风险。通过多目标优化,我们可以设计出既能快速执行又有着较高准确度的决策树模型,以适应高频交易环境的需求。
通过这一节的深入探讨,我们看到了决策树不仅仅是一个简单的分类或回归工具,而是一个可扩展的、能与其他算法相结合、并且能够适应复杂应用需求的强大机器学习方法。
四、案例实战
在本节中,我们将通过一个实战案例来展示如何使用Python和PyTorch实现决策树算法。我们将使用一个公开的银行营销数据集,目标是预测客户是否会订阅定期存款。这是一个典型的二分类问题。
场景描述
假设我们是一家银行,希望建立一个模型来预测哪些客户更有可能订阅定期存款。成功预测出这些客户可以帮助银行更精准地进行营销,提高资源利用效率。
数据预处理
在开始之前,我们需要进行数据预处理,包括加载数据、清洗数据、进行特征编码等。
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import LabelEncoder
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score# 加载数据
data = pd.read_csv('bank.csv', sep=';')# 数据预处理
# 将分类变量转换为数值
labelencoder = LabelEncoder()
data['job'] = labelencoder.fit_transform(data['job'])
data['marital'] = labelencoder.fit_transform(data['marital'])
# ...对其他分类变量进行编码# 定义特征集和标签
X = data.iloc[:, :-1].values
y = data.iloc[:, -1].values# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
决策树模型
下面,我们将使用DecisionTreeClassifier来训练模型,并对其进行评估。
# 创建决策树分类器实例
clf = DecisionTreeClassifier(criterion='entropy', random_state=42)# 训练模型
clf.fit(X_train, y_train)# 在测试集上进行预测
y_pred = clf.predict(X_test)# 评估模型
accuracy = accuracy_score(y_test, y_pred)
print(f'模型准确率: {accuracy:.2f}')
结果分析
这段代码会输出模型的准确率,作为评估其性能的指标。在现实应用中,我们还会关注模型的召回率、精确率和F1分数,以及通过混淆矩阵来进一步分析模型的性能。
在这个案例中,决策树模型可以帮助银行预测客户是否会订阅定期存款。通过准确率的高低,我们可以了解到模型在解决实际问题上的有效性。
输出展示
输出将直接显示模型在测试数据上的准确率,为银行提供了一个量化的工具来判断营销活动的潜在效果。
实际操作中,模型的输出还会进一步转换为决策支持,例如,通过模型预测的概率阈值来确定是否对某个客户进行营销活动。
总结
通过这个案例,我们展示了如何使用Python实现一个简单的决策树分类器,以及如何应用它在实际的商业场景中进行决策。这个实战案例仅是决策树应用的冰山一角,决策树的强大和灵活性使其在各种不同的领域都有广泛的应用。
五、总结
决策树算法作为机器学习领域的基石之一,其直观性和易于解释的特性为其赢得了广泛的应用。本文从决策树的基础知识出发,逐步深入到算法优化、研究进展,最终以一个实战案例来集中展示其在实际问题中的应用。
在技术的深度和复杂性不断提高的今天,决策树算法仍然保持着其独特的魅力。它能够与新兴的机器学习技术如深度学习、强化学习等相结合,创造出更为强大和适应性强的模型。例如,通过集成学习中的随机森林或提升方法,决策树的预测性能得到了显著提升,同时保留了模型的可解释性。
决策树的结构使其成为理解数据属性和做出预测决策的有力工具,尤其是在需要快速决策和解释决策过程的场景中。这对于处在法规要求高透明度决策过程的行业,如金融和医疗保健,尤为重要。
然而,决策树算法并不是没有挑战。过拟合和处理高维数据时的效率问题是其两大主要的技术难题。尽管存在这些挑战,但随着算法研究的不断深入,例如引入剪枝技术、特征选择和多目标优化等方法,我们有望设计出更为高效和鲁棒的决策树模型。
在案例实战中,我们利用Python和PyTorch展示了如何具体实现和应用决策树,这样的实操经验对于理解算法的实际效果和限制至关重要。
最后,可以预见,决策树算法将继续在人工智能的各个领域发挥其独特的价值。其简单、高效和易于解释的特点,将使其在可解释的AI(XAI)领域发挥重要作用,助力人类构建更加公正、透明和可信的机器学习系统。
相关文章:

大数据机器学习深度解读决策树算法:技术全解与案例实战
大数据机器学习深度解读决策树算法:技术全解与案例实战 本文深入探讨了机器学习中的决策树算法,从基础概念到高级研究进展,再到实战案例应用,全面解析了决策树的理论及其在现实世界问题中的实际效能。通过技术细节和案例实践&…...
【开源Mongdb驱动】SpringBoot+Mybatis+Mongdb融合使用教程
#【开源Mongdb驱动】SpringBootMybatisMongdb无缝融合使用教程 介绍 本文介绍一款基于JAVA开源的mongodb jdbc驱动为基础的无缝与springbootmybatis融合使用案例 mongodb JDBC 使用案例 https://blog.csdn.net/gongbing798930123/article/details/135002530 《基于开源的JA…...
freeRTOS使用
创建第一个FreeRTOS程序 1、官网源码下载 (1)进入FreeRTOS官网FreeRTOS professional services for application and RTOS development and consulting. FreeRTOS is an Open Source Code RTOS (2)点击下载FreeRTOS 2、处理目录 &…...
基于vue的线上点餐系统论文
基于vue的线上点餐系统 摘要 随着信息技术在管理上越来越深入而广泛的应用,管理信息系统的实施在技术上已逐步成熟。本文介绍了线上点餐系统的开发全过程。通过分析线上点餐系统管理的不足,创建了一个计算机管理线上点餐系统的方案。文章介绍了线上点餐…...
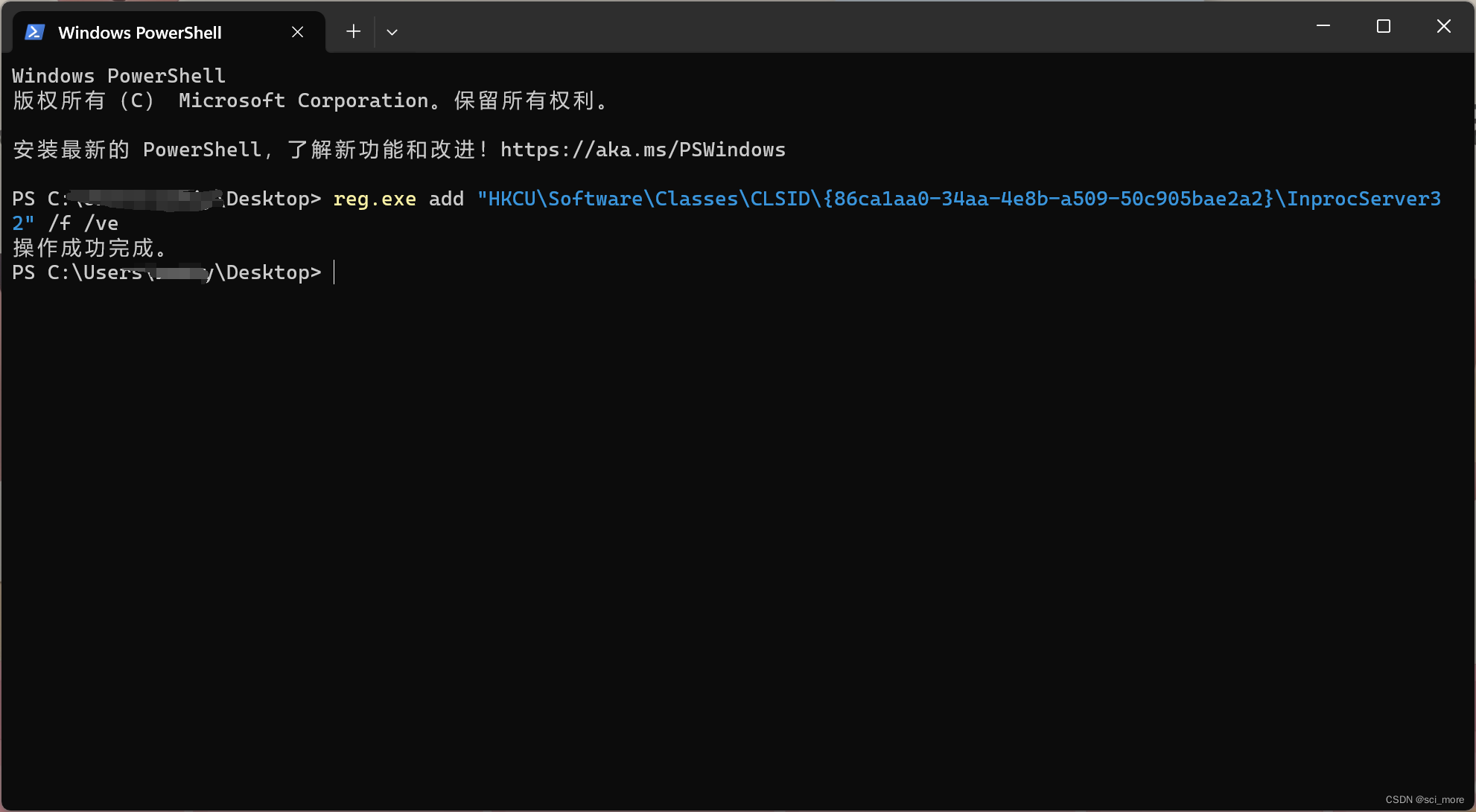
【Windows】windows11右键默认显示更多选项的办法
Windows11系统的右键菜单显示,需要多点一次“显示更多选项”才能看到所有菜单内容,按下面步骤简单设置一下就能恢复成Windows经典的右键菜单显示。 1. 2.输入命令【reg.exe add "HKCU\Software\Classes\CLSID\{86ca1aa0-34aa-4e8b-a509-50c905bae2a…...

推荐使用过很好用的api,含免费次数
IP归属地-IPv4城市级:根据IP地址查询归属地信息,支持到城市级,包含国家、省、市、和运营商等信息。IP归属地-IPv6城市级:根据IP地址(IPv6版本)查询归属地信息,支持到中国大陆地区(不…...

QT最大线程并发
声明一个处理函数;int timeTask(); 头文件: #include <QtConcurrent> #include <QFuture> 并发处理改函数的任务,直到处理完成: QFuture<int> ft QtConcurrent::run(this, &ch72_concurrent::timeTask);while (!f…...
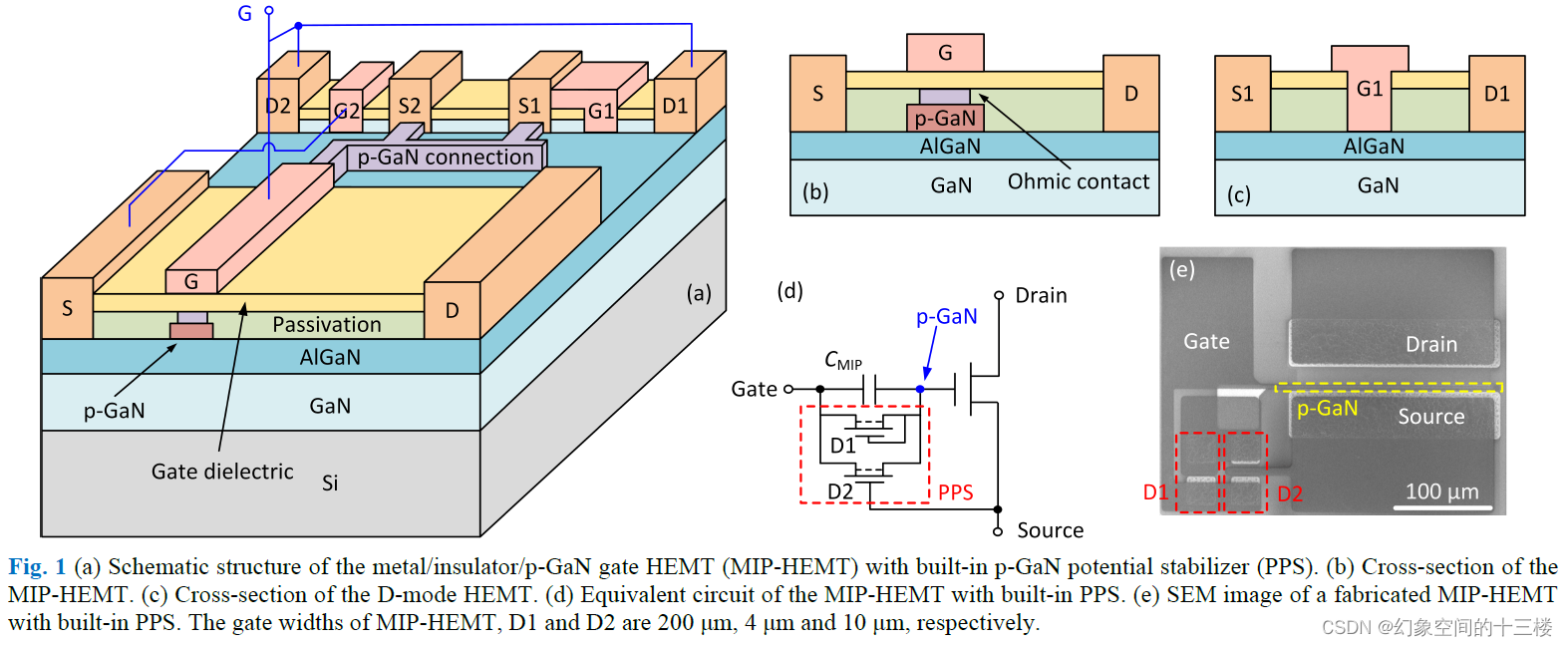
在金属/绝缘体/p-GaN栅极高电子迁移率晶体管中同时实现大的栅压摆幅和增强的阈值电压稳定性
标题:Simultaneously Achieving Large Gate Swing and Enhanced Threshold Voltage Stability in Metal/Insulator/p-GaN Gate HEMT (IEDM2023) 摘要 摘要:对于增强型GaN功率晶体管的发展,栅压摆幅和阈值电压稳定性通常是互相排斥的。本文展…...
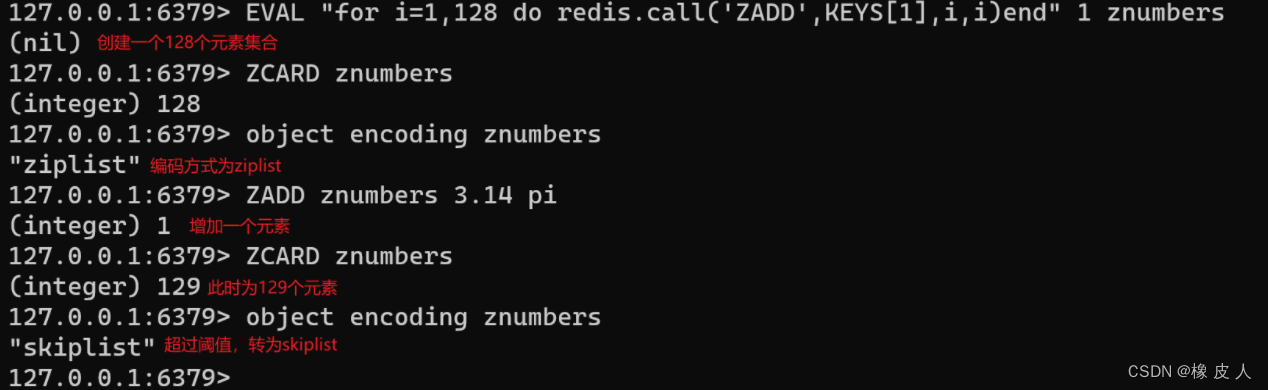
Redis第1讲——入门简介
Java并发编程的总结和学习算是告一段落了,这段时间思来想去,还是决定把Redis再巩固和学习一下。毕竟Redis不论是在面试还是实际应用中都是极其重要的,在面试中诸如Redis的缓存问题、热key、大key、过期策略、持久化机制等;还有在实…...

数据科学知识库
我的博客是一个技术分享平台,涵盖了机器学习、数据可视化、大数据分析、数学统计学、推荐算法、Linux命令及环境搭建,以及Kafka、Flask、FastAPI、Docker等组件的使用教程。 在这个信息时代,数据已经成为了一种新的资源,而机…...
设计模式——责任链模式(行为模式)
引言 责任链模式是一种行为设计模式, 允许你将请求沿着处理者链进行发送。 收到请求后, 每个处理者均可对请求进行处理, 或将其传递给链上的下个处理者。 问题 假如你正在开发一个在线订购系统。 你希望对系统访问进行限制, 只允…...
【谭浩强C语言:前八章编程题(多解)】
文章目录 第一章1. 求两个整数之和(p7) 第二章2. 求三个数中的较大值(用函数)(p14、p107)3.求123...n(求n的阶乘,用for循环与while循环)(P17)1.循环求n的阶乘2.递归求n的阶乘(n< 10) 4.有M个学生,输出成绩在80分以上的学生的学…...
程序人生15年人生感悟
计算机程序员并不是一件什么高大上的职业。而仅仅是一份普通的工作。就像医生能治病救人,我们能治蓝屏救程序,我们都在为这个世界默默的做出自己的贡献。刻意或无意宣扬某个职业高大上,其实质是对其它行业从业者的不公平。但是有些人却常常这…...

React与AJAX
大家好,欢迎来到 《React与AJAX》 课程。在这一课中,我们将学习如何在 React 中使用 AJAX。 什么是 AJAX? AJAX(Asynchronous JavaScript and XML)是一种使用 JavaScript 在浏览器和服务器之间进行异步通信的技术。A…...

C++ STL泛型算法
泛型算法 <algorithm>定义了大约 80 个标准算法。 它们操作由一对迭代器定义的(输入)序列或单一迭代器定义的(输出)序列。 当对两个序列进行拷贝、比较操作时,第一个序列由一对迭代器[b,e)表示,但第…...

使用OpenSSL生成PKCS#12格式的证书和私钥
要使用OpenSSL生成PKCS12格式的证书和私钥,可以按照以下步骤进行操作: 1. 安装OpenSSL 首先,确保已在计算机上安装了OpenSSL。可以从OpenSSL官方网站(https://www.openssl.org/)下载并安装适用于您的操作系统的版本。…...
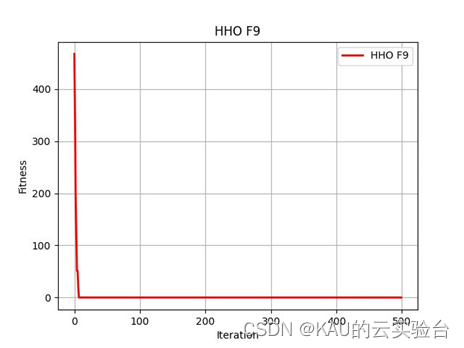
超详细 | 哈里斯鹰优化算法原理、实现及其改进与利用(Matlab/Python)
测试函数为F9 在MATLAB中执行程序结果如下: 在Python中执行程序结果如下: 哈里斯鹰优化算法(Harris Hawks Optimization , HHO)是 Heidari等[1]于2019年提出的一种新型元启发式算法,设计灵感来源于哈里斯鹰在捕食猎物过程中的合作行为以及突…...

git 切换远程地址分支 推送到指定地址分支 版本回退
切换远程地址 1、切换远程仓库地址: 方式一:修改远程仓库地址 【git remote set-url origin URL】 更换远程仓库地址,URL为新地址。 git remote set-url https://gitee.com/xxss/omj_gateway.git 方式二:先删除远程仓库地址&…...

YOLOv3-YOLOv8的一些总结
0 写在前面 这个文档主要总结YOLO系列的创新点,以YOLOv3为baseline。参考(抄)了不少博客,就自己看看吧。有些模型的trick不感兴趣就没写进来,核心的都写了。 YOLO系列的网络都由四个部分组成:Input、Backbone、Neck、Prediction…...

鸿蒙(HarmonyOS)项目方舟框架(ArkUI)控件的部分公共属性和事件
鸿蒙(HarmonyOS)项目方舟框架(ArkUI)控件的部分公共属性和事件 一、操作环境 操作系统: Windows 10 专业版 IDE:DevEco Studio 3.1 SDK:HarmonyOS 3.1 二、公共属性 常用的公共属性有: 宽(with)、高(height)、…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...

Kubernetes 节点自动伸缩(Cluster Autoscaler)原理与实践
在 Kubernetes 集群中,如何在保障应用高可用的同时有效地管理资源,一直是运维人员和开发者关注的重点。随着微服务架构的普及,集群内各个服务的负载波动日趋明显,传统的手动扩缩容方式已无法满足实时性和弹性需求。 Cluster Auto…...
