【数据结构】——排序算法简答题模板
目录
- 一、内排序和外排序
- 二、排序算法的稳定性
- 三、插入排序
- (一)直接插入排序的步骤
- (二)直接插入排序的稳定性
- (三)折半插入排序的步骤
- (四)希尔排序的步骤
- 四、交换排序
- (一)冒泡排序的步骤
- (二)冒泡排序的趟数和比较次数
- (三)快速排序的步骤
- (四)快速排序的稳定性
- 五、堆排序
- (一)堆排序的步骤
- (二)堆排序的稳定性
- (三)堆排序的时间复杂度
- 六、归并排序
- (一)k路归并排序的步骤
- (二)k路归并排序的稳定性
- (三)二路归并排序的步骤
- 七、排序算法的综合运用
一、内排序和外排序
1、内排序和外排序有什么区别?内排序有哪些算法?
答:根据排序过程中,数据元素是否完全在内存中进行,可分为内排序和外排序。内排序有直接/折半插入排序、简单旋转排序、冒泡排序、希尔排序、快速排序和堆排序。
二、排序算法的稳定性
1、什么是稳定排序?
答:经过排序后能使关键字相同的元素保持原本顺序中的相对位置不变,则称这个算法是稳定的,反之则不稳定。
三、插入排序
(一)直接插入排序的步骤
1、简述直接插入排序算法的基本思想。
答:直接插入排序是将要排序的序列按照关键字的大小插入至已排好序的子序列中,一直进行直到整个序列有序。
(二)直接插入排序的稳定性
1、直接插入排序算法是不是稳定的排序方法?
答:由于每次插入元素时总是从后向前比较后再移动,所以不会出现相同元素相对位置发生变化的情况,即直接插入排序是稳定的。
(三)折半插入排序的步骤
1、简述折半插入排序算法的基本思想。
答:折半插入排序的具体步骤如下:
初始化一个已排序序列,该序列只包含第一个元素,从第二个元素开始,通过折半查找确定每个待排序元素的插入位置,根据已排序序列中元素的中点,比较待排序元素与中点元素的大小,若待排序元素大于中点元素,则插入位置在中间位置的右侧;否则,插入位置在中间位置的左侧,然后插入元素,同时,需要将插入位置及其之后的所有元素向后移动一位,以为待排序元素腾出空间,重复步骤,直到所有元素都被插入到已排序序列中。
(四)希尔排序的步骤
1、简述希尔排序的基本思想。
答:希尔排序也称为缩小增量排序,即通过选取一定的增量来排序的,本质还是插入排序,通过增量将序列分为几个子序列,然后对每个子序列进行直接插入排序。
四、交换排序
(一)冒泡排序的步骤
1、简述冒泡排序的步骤。
答:通过两两比较相邻的元素,若发生逆序,则进行交换,直到整个序列有序为止,即若某一趟冒泡排序中没有发生元素交换,说明此时序列已整体有序。
(二)冒泡排序的趟数和比较次数
1、设有n 个元素采用冒泡排序法进行排序,通常需要进行多少趟排序?对于第i 次冒泡通常需要进行多少次关键字比较?
答:n个元素采用冒泡排序进行排序,最多需要进行n-1趟排序,即最坏情况下,排好的序列刚好与初始序列相反,呈逆序排列;而最少是初始序列正序,只需一趟即可完成排序。
2、设有n 个元素采用冒泡排序法进行排序,第i 次冒泡通常需要进行多少次关键字比较?
答:最好情况下,比较次数为n-1;最坏情况下,由于需要进行n-1趟排序,第i趟排序中要进行n-i次比较。
(三)快速排序的步骤
1、简述快速排序的步骤。
答:快速排序又称为分区交换排序,通过多次划分操作来实现排序思想,其步骤如下:
①每一趟排序中选取一个关键字作为枢轴;
②枢轴将待排序的序列分为两个部分,比枢轴小的元素移到其前,比枢轴大的元素移到其后,这是一趟快速排序;
③然后递归地对两个部分按照枢轴划分规则继续进行快速排序,直至每个区域只有一个元素为止或序列为空,最后达到整个序列有序。
(四)快速排序的稳定性
1、试举例说明快速排序的稳定性。
答:快速排序是不稳定的。当快速排序在处理包含有相等的元素的数组时,相等元素的值没有改变,但它们的相对顺序已经发生了变化,从而导致排序结果不稳定。
五、堆排序
(一)堆排序的步骤
1、简述堆排序的基本思想。
答:堆排序的基本思想是利用大根堆(小根堆)进行排序的方法,步骤如下:
①将待排序的序列构造成一个大根堆(小根堆),此时,整个序列的最大值(最小值)即为堆的根结点。
②将当前根结点移走,即与堆数组的末尾元素交换,此时末尾元素就是最大值(最小值),然后将剩余的n-1个序列重新构造成一个堆,依次得到n个元素中的次大值(次小值);
③重复以上步骤,从而得到一个有序序列。
(二)堆排序的稳定性
1、堆排序是不是稳定排序?
答:堆排序不是,因为在进行筛选时可能会将后面相同关键字的元素调整到前面,所有不是稳定的排序算法。
(三)堆排序的时间复杂度
1、设结点个数为 n,采用堆排序法进行排序,其时间复杂性是多少?
答:堆排序的时间复杂性取决于堆的构造和调整过程,将结点个数为n的初始序列构造成一个大根堆或小根堆,建堆过程中元素比较次数最多为4n,由于需要遍历整个序列,所以这个构造过程的时间复杂度为O(n)。然后,从剩余n-1个元素中选出一个最大或最小的元素,与末尾元素交换,这样的步骤最多需要n-1次,所以复杂度是n(n-1)/2次对数级别的比较,但是需要减去n/2的建堆时间,即排序过程的时间复杂度为O(nlog2n),所以总的堆排序的时间复杂度为O(n)+O(nlog2n)=O(nlog2n)。
六、归并排序
(一)k路归并排序的步骤
1、什么是归并排序?
答:将已有序的子序列合并,得到完全有序的序列,其中先使每个子序列有序,再使子序列间有序,即为归并排序。
(二)k路归并排序的稳定性
1、归并排序是不是稳定的?
答:归并排序是稳定的排序算法,满足稳定算法的定义,即假设在数列中存在a[i]=a[j],若在排序之前,a[i]在a[j]前面,且排序之后,a[i]仍然在a[j]前面。
(三)二路归并排序的步骤
1、简述二路归并排序的算法思想。
答:二路归并排序的步骤如下:
①将含n个元素的序列分为由n个长度为1的有序子表;
②相邻的两个有序子表归并为一个有序子表(两两相邻归并);
③重复以上步骤,最终归并成一个长度为n的有序表。
七、排序算法的综合运用
1、现有一文件F含有 1000 个记录,其中只有少量记录次序不对,且它们距离正确位置不远如果以比较和移动次数作为度量,那么将其排序最好采用什么方法?为什么?
答:由于文件中基本都是有序的,只有少量记录次序不正确,所以可以通过直接插入排序,它在初始序列已基本有序的情况下表现较好,即在每一步中,只需要移动很少的记录,而不像其他排序算法可能需要交换多个记录。因为只需要比较和交换记录的位置,所以比较次数较少,且由于距离正确位置不远,从而使通过直接插入排序的移动次数也较少,所以选择直接插入排序。
2、全国有 10000 人参加物理竞赛,只录取成绩优异的前 10 名,将他们从高分到低分输出。而对落选的其他考生,不需排出名次,问此种情况下,用何种排序方法速度最快?为什么?
答:堆排序。一般在n个元素中选出k(k<<n,k>2)个最大(或最小)元素时,均采用堆排序,且堆排序建堆时的最多比较次数为4n,而其他排序算法的时间复杂度较高。
相关文章:

【数据结构】——排序算法简答题模板
目录 一、内排序和外排序二、排序算法的稳定性三、插入排序(一)直接插入排序的步骤(二)直接插入排序的稳定性(三)折半插入排序的步骤(四)希尔排序的步骤 四、交换排序(一…...

vue3.0基础
1. setup函数 vue单页面使用到的变量和方法都定义在setup函数中,return后才能被页面引用 export default {setup(){const name 张三const person {name,age:30}function goWork(){consle.log(工作)}return {name,person,goWork}} } 注意:直接定义的变量修改不会…...

Kafka本地安装⭐️(Windows)并测试生产消息以及消费消息的可用性
2023.12.17 天气晴 温度较低 十点半,不是不想起实在是阳光浴太nice了日常三连,喂,刷,肝刷会儿博客,看会儿设计模式冷冷冷 进被窝 刷视频 睡觉看看kafka的本地部署 》》实践》》成功写会儿博客,…...

生产环境_Spark解析JSON字符串并插入到MySQL数据库
业务背景: 最近开发有一个需求,是这样的 我需要将一段从前端传过来的JSON字符串进行解析,并从中提取出所需的数据,然后将这些数据插入到MySQL数据库中。 json格式样例如下 { \"区域编号\": \"001\", …...

WEB渗透—PHP反序列化(四)
Web渗透—PHP反序列化 课程学习分享(课程非本人制作,仅提供学习分享) 靶场下载地址:GitHub - mcc0624/php_ser_Class: php反序列化靶场课程,基于课程制作的靶场 课程地址:PHP反序列化漏洞学习_哔哩…...
LVS-DR模式部署
实验准备: 节点服务器 192.168.116.20 #web1 192.168.116.30 #web2 1.部署NFS共享存储 2.部署Web节点服务器 将两台服务器的网关注释掉 #重启网卡 systemctl restart network 修改节点服务器的内核参数|vim /etc/sysctl.conf net.ipv4.conf.lo.arp_ign…...
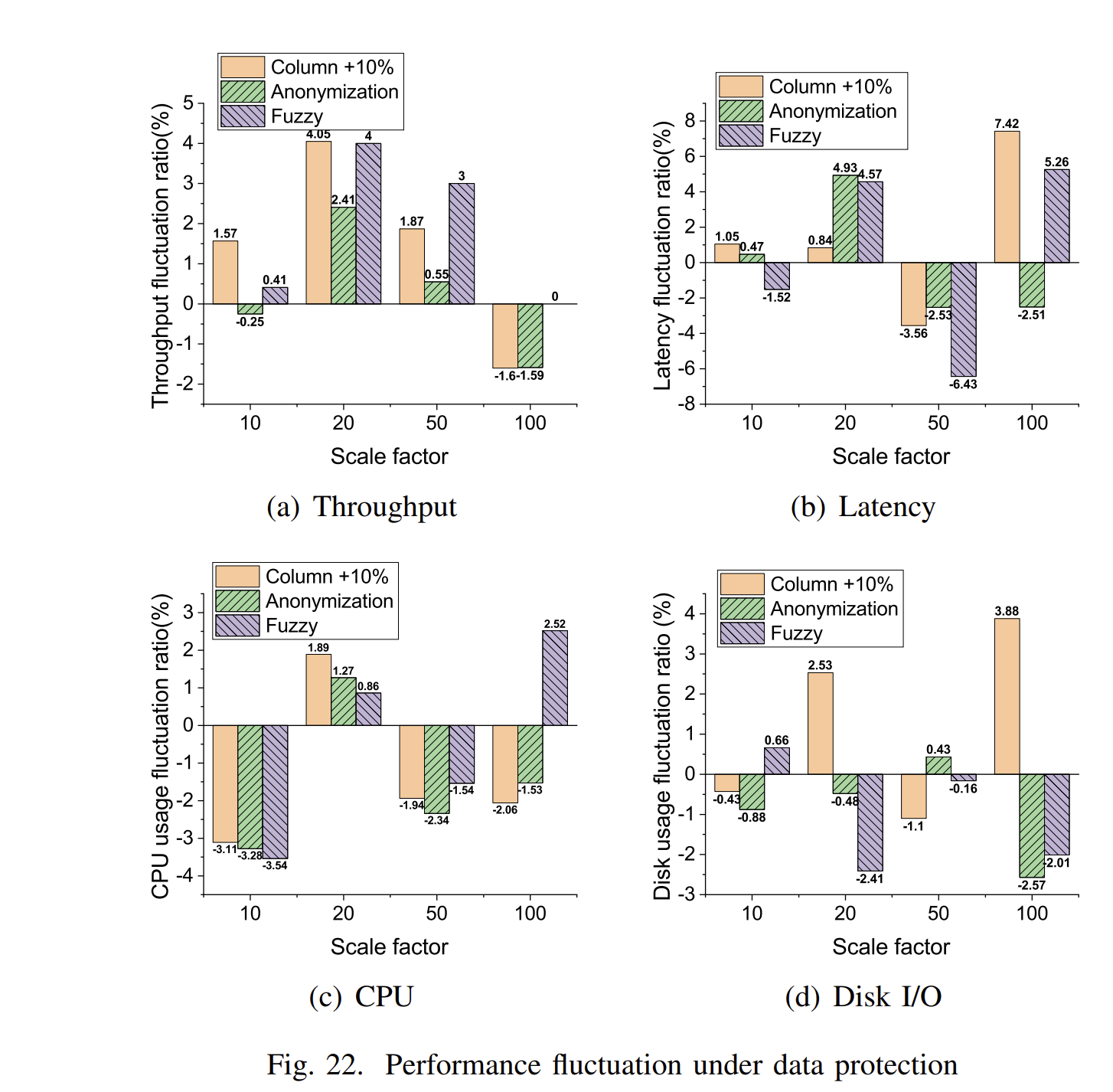
Oracle的学习心得和知识总结(三十)| OLTP 应用程序的合成工作负载生成器Lauca论文翻译及学习
目录结构 注:提前言明 本文借鉴了以下博主、书籍或网站的内容,其列表如下: 1、参考书籍:《Oracle Database SQL Language Reference》 2、参考书籍:《PostgreSQL中文手册》 3、EDB Postgres Advanced Server User Gui…...

HarmonyOS4.0从零开始的开发教程18后台代理提醒
HarmonyOS(十六)后台代理提醒 简介 随着生活节奏的加快,我们有时会忘记一些重要的事情或日子,所以提醒功能必不可少。应用可能需要在指定的时刻,向用户发送一些业务提醒通知。例如购物类应用,希望在指定时…...

智能优化算法应用:基于算术优化算法3D无线传感器网络(WSN)覆盖优化 - 附代码
智能优化算法应用:基于算术优化算法3D无线传感器网络(WSN)覆盖优化 - 附代码 文章目录 智能优化算法应用:基于算术优化算法3D无线传感器网络(WSN)覆盖优化 - 附代码1.无线传感网络节点模型2.覆盖数学模型及分析3.算术优化算法4.实验参数设定5.算法结果6.…...
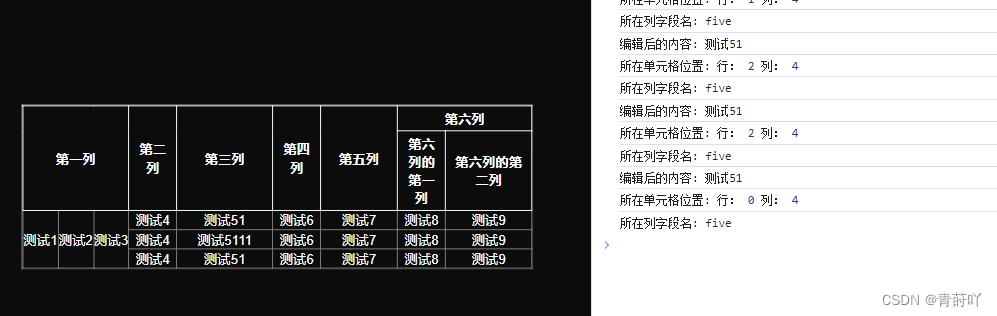
在vue中通过js动态绘制table,并且合并连续相同内容的行,支持点击编辑单元格内容
首先是vue代码 <template><div id"body-container"style"position: absolute"><div class"box-container"><div class"lsb-table-box" ><div class"table-container" id"lsb-table"&…...

输电线路定位:精确导航,确保电力传输安全
在现代社会中,电力作为生活的基石,其安全稳定运行至关重要。而输电线路作为电力传输的重要通道,其故障定位和修复显得尤为重要。恒峰智慧科技将为您介绍一种采用分布式行波测量技术的输电线路定位方法,以提高故障定位精度…...

ZKP Commitment (1)
MIT IAP 2023 Modern Zero Knowledge Cryptography课程笔记 Lecture 5: Commitment 1 (Ying Tong Lai) Overview: Modern SNARK IOP: Interactive Oracle ProofCommitment SchemeIOP “compiled by” the commitment scheme to get a non-interactive proofAn IOP is “inform…...

【难点】【LRU】146.LRU缓存
题目 法1:基于Java的LinkedHashMap 必须掌握法1。参考链接 关于LinkedHashMap的介绍 class LRUCache {int cap;LinkedHashMap<Integer, Integer> cache new LinkedHashMap<>();public LRUCache(int capacity) { this.cap capacity;}public int get…...
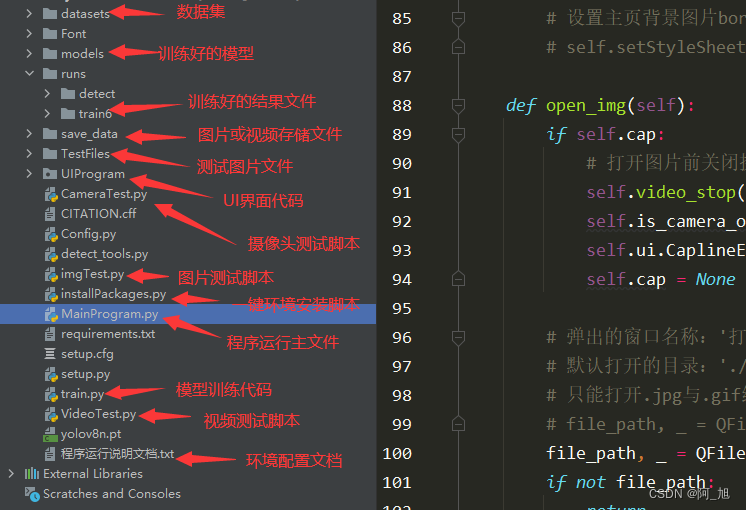
基于YOLOv8深度学习的吸烟/抽烟行为检测系统【python源码+Pyqt5界面+数据集+训练代码】目标检测、深度学习实战
《博主简介》 小伙伴们好,我是阿旭。专注于人工智能、AIGC、python、计算机视觉相关分享研究。 ✌更多学习资源,可关注公-仲-hao:【阿旭算法与机器学习】,共同学习交流~ 👍感谢小伙伴们点赞、关注! 《------往期经典推…...

菜鸟学习日记(python)——匿名函数
Python 使用 lambda 来创建匿名函数。 lambda 函数是一种小型、匿名的内联函数,它可以具有任意数量的参数,但只能有一个表达式。 匿名函数的一般格式如下: lambda 参数列表:表达式 表达式用于计算并返回函数结果 lambda 函数通常用于编写…...

CompleteFuture与Future的比较
CompleteFuture的介绍CompleteFuture的特点CompleteFuture的应用场景CompletableFuture的优缺点Future的介绍Future的特点Future的应用场景Future的优缺点CompletableFuture和Future的区别CompletableFuture和Future的关联关系CompletableFuture和Future的使用示例CompletableF…...

数据分享 I 全国市级商品房屋销售数据,shp/excel格式,2005-2020年数据
基本信息. 数据名称: 全国市级商品房屋销售数据 数据格式: Shp、excel 数据时间: 2005-2020年 数据几何类型: 面 数据坐标系: WGS84坐标系 数据来源:网络公开数据 数据字段: 序号字段名称字段说明1spxse商品房销售额(亿元…...
【C++】【华清远见西安中心】)
面试题总结(十一)【C++】【华清远见西安中心】
C和C的区别有哪些? C 和 C 是两种不同的编程语言,它们有以下一些区别: 1. 语言起源和发展:C 语言是由贝尔实验室的 Dennis Ritchie 在 1972 年开发的,主要用于系统编程和底层开发;而 C 语言是在 C 语言的基…...

c++_01_名字空间_复合类型_缺省参数_哑元函数
0 前言 C和C一样,都属于编译型语言 C和C一样,都属于强类型语言 C对C完全兼容,并提供更多面向对象的特性:语言风格更加简洁,类型检查更加严格 1 名字空间 namespace WHY?划分更精细的逻辑单元(逻辑空间)&…...

前端常见面试题之html和css篇
文章目录 一、html1. 如何理解html语义化2. 说说块级元素和内联元素的区别 二、css1. 盒模型的宽度offsetWidth如何计算2. box-sizing:border-box有什么用3. margin的纵向重叠问题4. 谈谈你对BFC的理解和应用5. 清除浮动有哪些方式6. 使用flex布局实现骰子37.position的absolut…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

GraphQL 实战篇:Apollo Client 配置与缓存
GraphQL 实战篇:Apollo Client 配置与缓存 上一篇:GraphQL 入门篇:基础查询语法 依旧和上一篇的笔记一样,主实操,没啥过多的细节讲解,代码具体在: https://github.com/GoldenaArcher/graphql…...
