机器学习 | 决策树 Decision Tree
—— 分而治之,逐个击破
把特征空间划分区域
每个区域拟合简单模型
分级分类决策
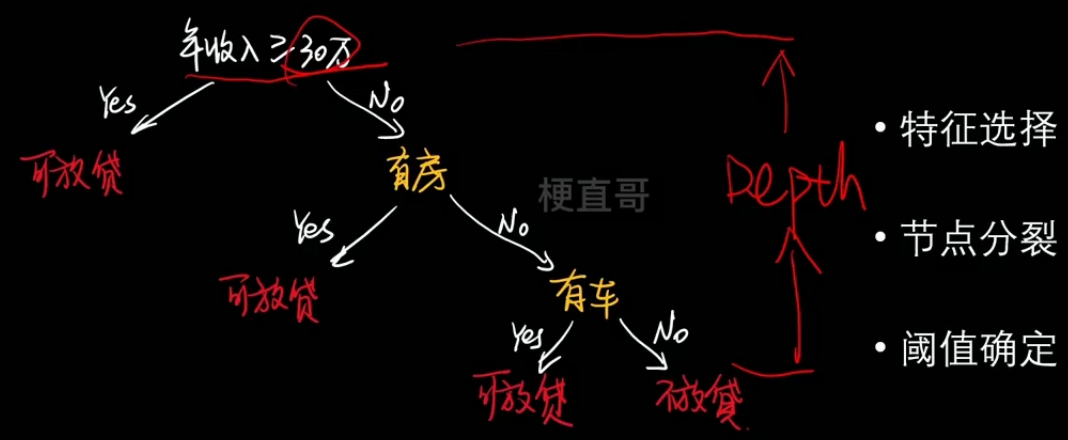
1、核心思想和原理

- 举例:
- 特征选择、节点分类、阈值确定
2、信息嫡
熵本身代表不确定性,是不确定性的一种度量。
熵越大,不确定性越高,信息量越高。
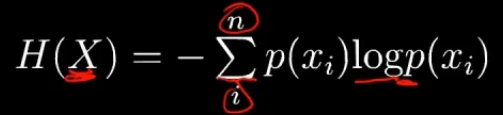
为什么用log?—— 两种解释,可能性的增长呈指数型;log可以将乘法变为加减法。
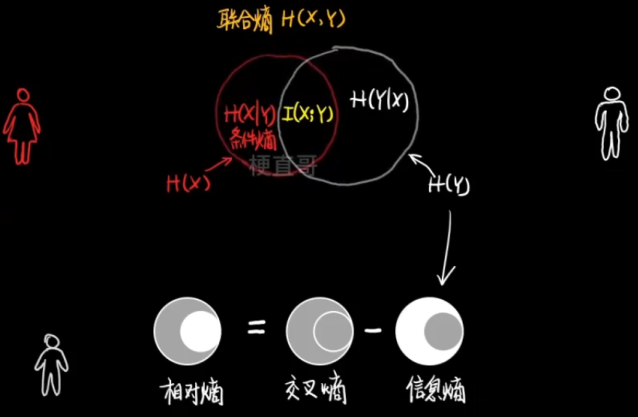
联合熵 的物理意义:观察一个多变量系统获得的信息量。
条件熵 的物理意义:知道其中一个变量的信息后,另一个变量的信息量。
给定了训练样本 X ,分类标签中包含的信息量是什么。

信息增益(互信息)
代表了一个特征能够为一个系统带来多少信息。

熵的分类

熵的本质:特殊的衡量分布的混乱程度与分散程度的距离
二分类信息熵:
二分类信息熵
import numpy as np
import matplotlib.pyplot as pltdef entropy(p):return -(p * np.log2(p) + (1 - p) * np.log2(1 - p))plot_x = np.linspace(0.001, 0.999, 100)
plt.plot(plot_x, entropy(plot_x))
plt.show() 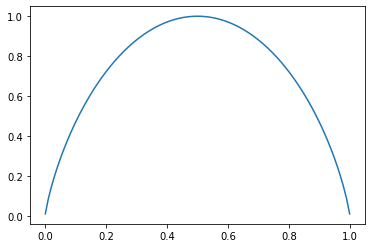
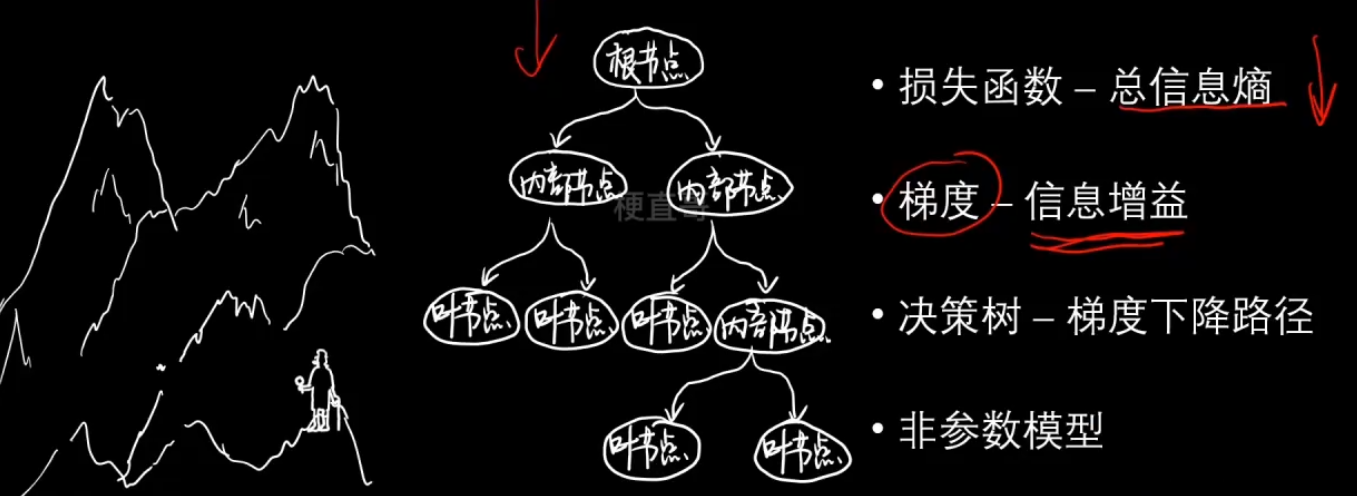
决策树的本质
3、决策树分类代码实现
数据集
from sklearn.datasets import load_irisiris = load_iris()
x = iris.data[:, 1:3]
y = iris.targetplt.scatter(x[:,0], x[:,1], c = y)
plt.show()
3.1、sklearn中的决策树
from sklearn.tree import DecisionTreeClassifierclf = DecisionTreeClassifier(max_depth=2, criterion='entropy')
clf.fit(x, y)DecisionTreeClassifier
DecisionTreeClassifier(criterion='entropy', max_depth=2)
决策边界绘制的代码:
def decision_boundary_plot(X, y, clf):axis_x1_min, axis_x1_max = X[:,0].min() - 1, X[:,0].max() + 1axis_x2_min, axis_x2_max = X[:,1].min() - 1, X[:,1].max() + 1x1, x2 = np.meshgrid( np.arange(axis_x1_min,axis_x1_max, 0.01) , np.arange(axis_x2_min,axis_x2_max, 0.01))z = clf.predict(np.c_[x1.ravel(),x2.ravel()])z = z.reshape(x1.shape)from matplotlib.colors import ListedColormapcustom_cmap = ListedColormap(['#F5B9EF','#BBFFBB','#F9F9CB'])plt.contourf(x1, x2, z, cmap=custom_cmap)plt.scatter(X[:,0], X[:,1], c=y)plt.show()decision_boundary_plot(x, y, clf)
from sklearn.tree import plot_tree
plot_tree(clf)[Text(0.4, 0.8333333333333334, 'X[1] <= 2.45\nentropy = 1.585\nsamples = 150\nvalue = [50, 50, 50]'),Text(0.2, 0.5, 'entropy = 0.0\nsamples = 50\nvalue = [50, 0, 0]'),Text(0.6, 0.5, 'X[1] <= 4.75\nentropy = 1.0\nsamples = 100\nvalue = [0, 50, 50]'),Text(0.4, 0.16666666666666666, 'entropy = 0.154\nsamples = 45\nvalue = [0, 44, 1]'),Text(0.8, 0.16666666666666666, 'entropy = 0.497\nsamples = 55\nvalue = [0, 6, 49]')]

3.2、最优划分条件
from collections import Counter
Counter(y)Counter({0: 50, 1: 50, 2: 50})
def calc_entropy(y):counter = Counter(y)sum_ent = 0for i in counter:p = counter[i] / len(y)sum_ent += (-p * np.log2(p))return sum_entcalc_entropy(y)1.584962500721156
def split_dataset(x, y, dim, value):index_left = (x[:, dim] <= value)index_right = (x[:, dim] > value)return x[index_left], y[index_left], x[index_right], y[index_right]def find_best_split(x, y):best_dim = -1best_value = -1best_entropy = np.infbest_entropy_left, best_entropy_right = -1, -1for dim in range(x.shape[1]):sorted_index = np.argsort(x[:, dim])for i in range(x.shape[0] - 1): # x列数value_left, value_right = x[sorted_index[i], dim], x[sorted_index[i + 1], dim]if value_left != value_right:value = (value_left + value_right) / 2x_left, y_left, x_right, y_right = split_dataset(x, y, dim, value)entropy_left, entropy_right = calc_entropy(y_left), calc_entropy(y_right)entropy = (len(x_left) * entropy_left + len(x_right) * entropy_right) / x.shape[0]if entropy < best_entropy:best_dim = dimbest_value = valuebest_entropy = entropybest_entropy_left, best_entropy_right = entropy_left, entropy_rightreturn best_dim, best_value, best_entropy, best_entropy_left, best_entropy_rightfind_best_split(x, y)(1, 2.45, 0.6666666666666666, 0.0, 1.0)
x_left, y_left, x_right, y_right = split_dataset(x, y, 1, 2.45)find_best_split(x_right, y_right)(1, 4.75, 0.34262624992678425, 0.15374218032876188, 0.4971677614160753)
4、基尼系数

基尼系数运算稍快;
物理意义略有不同,信息熵表示的是随机变量的不确定度;
基尼系数表示在样本集合中一个随机选中的样本被分错的概率,也就是纯度。
基尼系数越小,纯度越高。
模型效果上差异不大。
二分类信息熵和基尼系数代码实现:
import numpy as np
import matplotlib.pyplot as pltdef entropy(p):return -(p * np.log2(p) + (1 - p) * np.log2(1 - p))def gini(p):return 1 - p ** 2 - (1 - p) ** 2plot_x = np.linspace(0.001, 0.999, 100)
plt.plot(plot_x, entropy(plot_x), color = 'blue')
plt.plot(plot_x, gini(plot_x), color = 'red')
plt.show()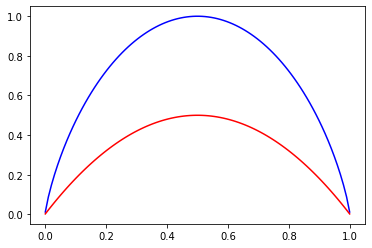
5、决策树剪枝
Chapter-07/7-6 决策树剪枝.ipynb · 梗直哥/Machine-Learning - Gitee.com
为什么要剪枝?
复杂度过高。
预测复杂度:O(logm)
训练复杂度:O(n x m x logm)
logm为数的深度,n为数据的维度。
容易过拟合
为非参数学习方法。
目标:
降低复杂度
解决过拟合
手段:
限制深度(结点层数)
限制广度(叶子结点个数)
—— 设置超参数

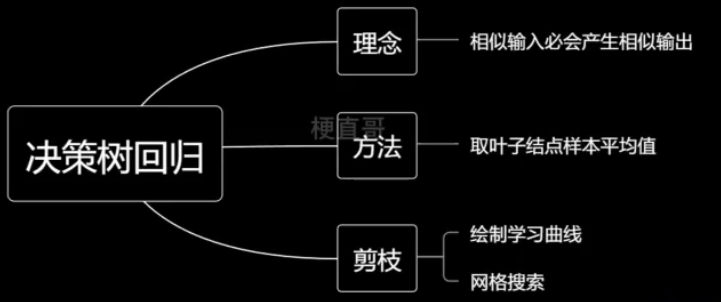
6、决策树回归
基于一种思想:相似输入必会产生相似输出。
取节点平均值。
6.1、决策树回归代码实现
import matplotlib.pyplot as plt
import numpy as npfrom sklearn import datasets
from sklearn.model_selection import train_test_split
import warnings
warnings.filterwarnings('ignore')boston = datasets.load_boston()
x = boston.data
y = boston.target
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=233)from sklearn.tree import DecisionTreeRegressorreg = DecisionTreeRegressor()
reg.fit(x_train,y_train)DecisionTreeRegressor
DecisionTreeRegressor()
reg.score(x_test,y_test)0.7410680140563546
reg.score(x_train,y_train)1.0
6.2、绘制学习曲线
from sklearn.metrics import r2_scoreplt.rcParams["figure.figsize"] = (12, 8)
max_depth = [2, 5, 10, 20]for i, depth in enumerate(max_depth):reg = DecisionTreeRegressor(max_depth=depth)train_error, test_error = [], []for k in range(len(x_train)):reg.fit(x_train[:k+1], y_train[:k+1])y_train_pred = reg.predict(x_train[:k + 1])train_error.append(r2_score(y_train[:k + 1], y_train_pred))y_test_pred = reg.predict(x_test)test_error.append(r2_score(y_test, y_test_pred))plt.subplot(2, 2, i + 1)plt.ylim(0, 1.1)plt.title("Depth: {0}".format(depth))plt.plot([k + 1 for k in range(len(x_train))], train_error, color = "red", label = 'train')plt.plot([k + 1 for k in range(len(x_train))], test_error, color = "blue", label = 'test')plt.legend()plt.show()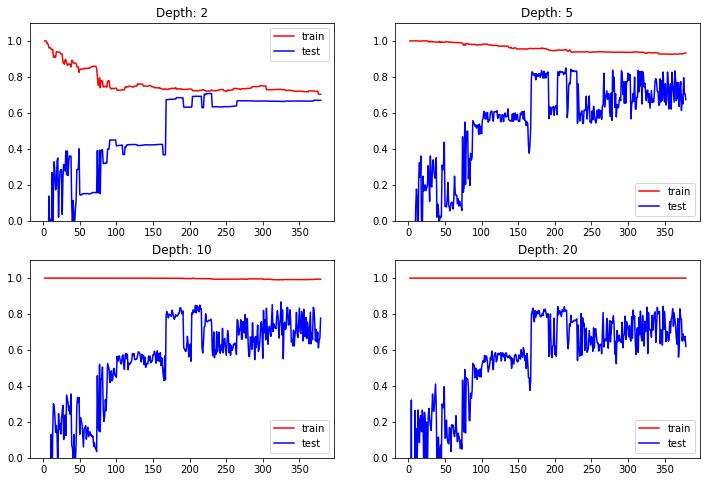
6.3、网格搜索
from sklearn.model_selection import GridSearchCVparams = {'max_depth': [n for n in range(2, 15)],'min_samples_leaf': [sn for sn in range(3, 20)],
}grid = GridSearchCV(estimator = DecisionTreeRegressor(), param_grid = params, n_jobs = -1
)grid.fit(x_train,y_train)GridSearchCV
GridSearchCV(estimator=DecisionTreeRegressor(), n_jobs=-1,param_grid={'max_depth': [2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13,14],'min_samples_leaf': [3, 4, 5, 6, 7, 8, 9, 10, 11, 12,13, 14, 15, 16, 17, 18, 19]})
estimator: DecisionTreeRegressor
DecisionTreeRegressor()
DecisionTreeRegressor
DecisionTreeRegressor()
grid.best_params_{'max_depth': 5, 'min_samples_leaf': 3}
grid.best_score_0.7327442904059717
reg = grid.best_estimator_reg.score(x_test, y_test)0.781690085676063
7、优缺点和适用条件
优点:
符合人类直观思维
可解释性强
能够处理数值型数据和分类型数据
能够处理多输出问题
缺点:
容易产生过拟合
决策边界只能是水平或竖直方向
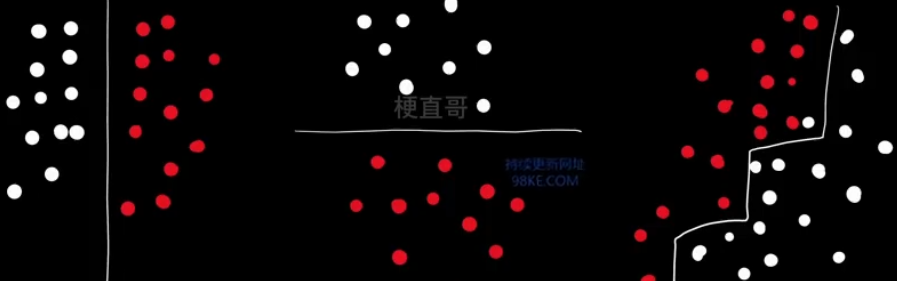
不稳定,数据的微小变化可能生成完全不同的树
参考于
Chapter-07/7-4 决策树分类.ipynb · 梗直哥/Machine-Learning - Gitee.com
相关文章:

机器学习 | 决策树 Decision Tree
—— 分而治之,逐个击破 把特征空间划分区域 每个区域拟合简单模型 分级分类决策 1、核心思想和原理 举例: 特征选择、节点分类、阈值确定 2、信息嫡 熵本身代表不确定性,是不确定性的一种度量。 熵越大,不确定性越高,…...
【系统移植】【华清远见西安中心】)
面试题总结(十四)【系统移植】【华清远见西安中心】
你用过哪些Bootloader?有什么区别? 作为一个AI助手,我没有直接使用过Bootloader。但我可以为您提供一些关于常见Bootloader的信息和他们之间的区别。 1. GRUB (GRand Unified Bootloader):GRUB是一个功能强大且广泛使用的Bootload…...

【Spark精讲】Spark RDD弹性体现在哪些方面?
什么是“弹性”? 一般对于分布式系统,“弹性”指的是可以根据计算规模进行动态伸缩的特性。当计算量增长时,可以动态增加资源来满足计算需求,而当计算量减少时,又可以降低资源配置来节约成本。 参考:什么是…...

【从客户端理解Kafka的使用方式】
文章目录 一、从基础的客户端说起1、消息发送者主流程2、消息消费者主流程 二、从客户端属性来梳理客户端工作机制1、消费者分组消费机制2、生产者拦截器机制3、消息序列化机制4、消息分区路由机制5、生产者消息缓存机制6、发送应答机制 三、客户端流程总结四、SpringBoot集成K…...
『OPEN3D』1.5.4 动手实现点云八叉树(OctoTree)最近邻
本专栏地址: https://blog.csdn.net/qq_41366026/category_12186023.html?spm=1001.2014.3001.5482 在二维和三维空间中,我们可以采用四叉树(Quad tree)和八叉树(Octree)这两种特定的数据结构来处理空间分割。这些树形结构可以看作是K-d树在不同维度下的扩展。…...

非制冷红外成像技术实现高灵敏度和高分辨率
非制冷红外成像技术实现高灵敏度和高分辨率主要依赖于以下几个方面: 探测器设计:非制冷红外成像技术采用的探测器通常具有高灵敏度和高分辨率的特点。这些探测器能够有效地接收并转换红外辐射,从而产生高质量的图像信息。 光学系统设计&…...

@Resource 和 @Autowired区别是什么?
Resource 和 Autowired 时,它们都是用于依赖注入的注解,但它们有一些不同之处。 来源: Resource 是Java EE标准的一部分,而且是JDK提供的,不属于Spring框架的注解。它的使用范围更广泛,不仅可以用在Spring中…...

K8S的一个pod中运行多个容器
通过deployment的方式部署 创建一个deployment文件 [rootk8s-master1 pods]# cat app.yaml apiVersion: apps/v1 kind: Deployment metadata:name: dsfnamespace: applabels:app: dsf spec:replicas: 1 #实例的个数selector:matc…...

《每天一分钟学习C语言·一》
1、转义字符:\n换行,\t前进一个tab键,\b退格键 2、八进制前面有0,%o或者%#o表示八进制,十六进制前有0X,%0x或者%#0x表示十六进制 3、%u打印无符号数,%g显示小数,类似于%fÿ…...
zookeeper:启动后占用8080端口问题解决
ZooKeeper是一个分布式的,开放源码的分布式应用程序协调服务。它为分布式应用提供一致性服务的软件,提供的功能包括:配置维护、域名服务、分布式同步、组服务等。 我们经常在运行zookeeper服务时,不需要配置服务端口,…...
深度学习中的高斯分布
1 高斯分布数学表达 1.1 什么是高斯分布 高斯分布(Gaussian Distribution)又称正态分布(Normal Distribution)。高斯分布是一种重要的模型,其广泛应用于连续型随机变量的分布中,在数据分析领域中高斯分布占有重要地位。由于中心极限定理(Central Limit…...

【已解决】Atlas 导入 Hive 元数据,执行 import-hive.sh 报错
部署完 Atlas 之后,尝试导入 Hive 元数据,遇到了一些错误,特此记录一下,方便你我他。 执行 import-hive.sh 报错 [omchadoop102 apache-atlas-2.2.0]$ hook-bin/import-hive.sh Using Hive configuration directory [/opt/module…...

在 Windows PC 上轻松下载并安装 FFmpeg
FFmpeg 是一种开源媒体工具,可用于将任何视频格式转换为您需要的格式。该工具只是命令行,因此它没有图形、可点击的界面。如果您习惯使用常规图形 Windows 程序,安装 FFmpeg 一开始可能看起来很复杂,但不用担心,它;很简…...

21.Servlet 技术
JavaWeb应用的概念 在Sun的Java Servlet规范中,对Java Web应用作了这样定义:“Java Web应用由一组Servlet、HTML页、类、以及其它可以被绑定的资源构成。它可以在各种供应商提供的实现Servlet规范的 Servlet容器 中运行。” Java Web应用中可以包含如下…...

【Hive】——DDL(PARTITION)
1 增加分区 1.1 添加一个分区 ALTER TABLE t_user_province ADD PARTITION (provinceBJ) location/user/hive/warehouse/test.db/t_user_province/provinceBJ;必须自己把数据加载到增加的分区中 hive不会帮你添加 1.2 一次添加多个分区 ALTER TABLE table_name ADD PARTITION…...

SpringBoot 源码解析4:事件监听器
SpringBoot 源码解析4:事件监听器 1. 初始化监听器2. 创建事件发布器 SpringApplicationRunListeners3. 事件分发流程3.1 SimpleApplicationEventMulticaster#multicastEvent3.2 获取监听器 AbstractApplicationEventMulticaster#getApplicationListeners3.3 Abstra…...

使用 FastAPI 和 Vue.js 实现前后端分离
简介 前后端分离是现代 Web 开发的趋势。使用 FastAPI 和 Vue.js 可以构建一个高效、灵活且易于维护的 Web 应用。FastAPI 提供了高性能的后端服务,而 Vue.js 作为一种渐进式 JavaScript 框架,可以构建动态的前端界面。本文将详细介绍如何使用 FastAPI …...

算法基础之SPFA判断负环
SPFA判断负环 核心思想:spfa算法 当遍历一个点时 cnt数组记录边数 若有负环 边数会无限1 cnt>n是即为有负环 #include<iostream>#include<cstring>#include<algorithm>#include<queue>using namespace std;const int N 2010 , M 10010…...
)
一些常用的Linux命令及其简要说明(持续更新)
1. cd:改变当前工作目录。 cd [directory]#例如 cd /home/user 2. ls:列出目录内容。 ls [-options] [file/directory]#例如 ls -l, ls /etc 3. pwd:显示当前工作目录。 pwd 4. mkdir:创建新目录。 mkdir [directory]#例…...
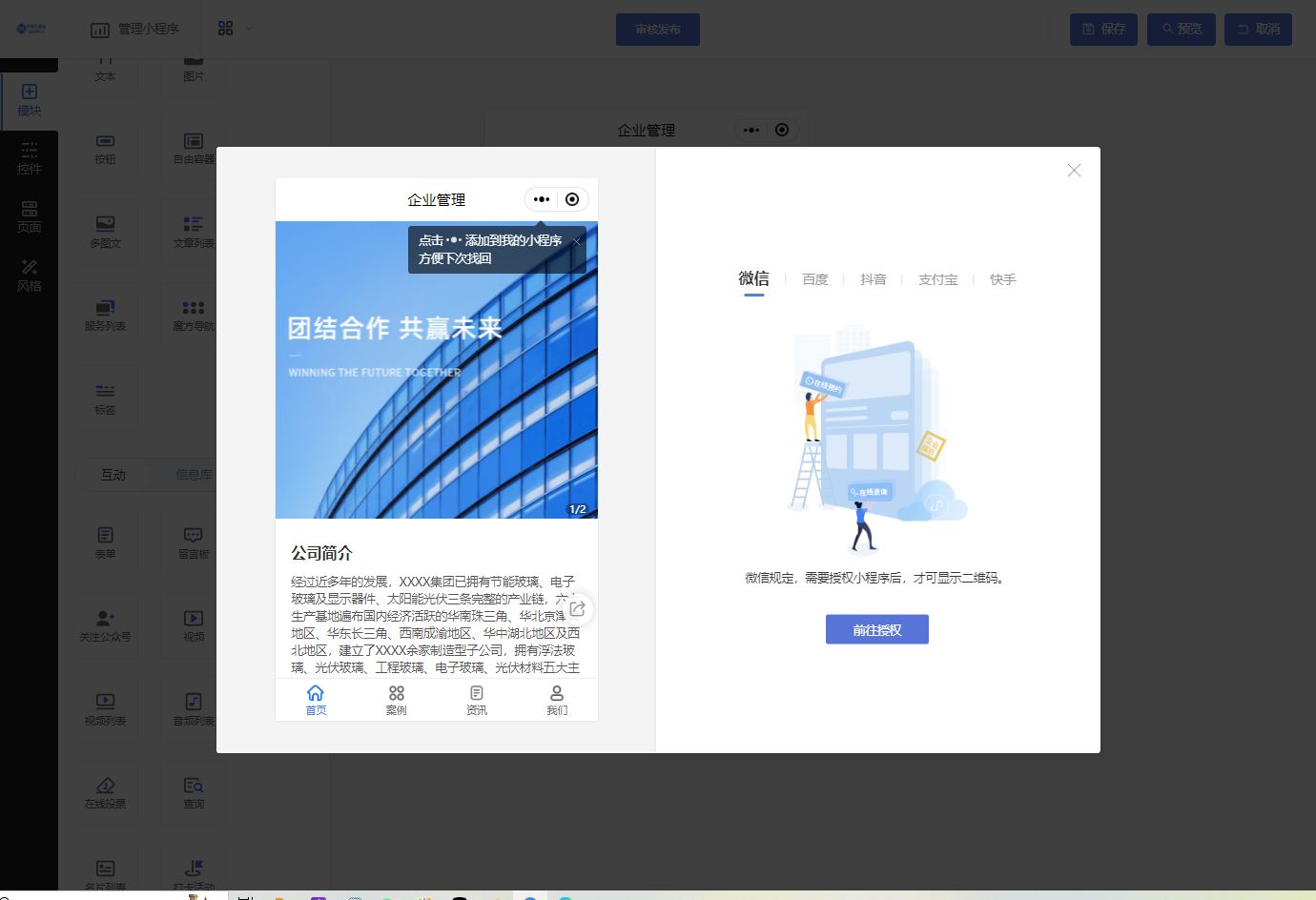
开发企业展示小程序的关键步骤和技巧
随着移动互联网的快速发展,小程序已经成为企业展示形象、推广产品和服务的重要工具。拥有一个优秀的小程序可以帮助企业提高品牌知名度,吸引更多潜在客户,提升用户体验。以下是拥有一个展示小程序的步骤: 确定需求和目标 首先&am…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...
