数据结构--稀疏矩阵及Java实现
一、稀疏 sparsearray 数组
1、先看一个实际的需求
- 编写的五子棋程序中,有存盘退出和续上盘的功能。

- 分析问题:
因为该二维数组的很多值是默认值 0, 因此记录了很多没有意义的数据.->稀疏数组。
2、稀疏数组基本介绍
当一个数组中大部分元素为0,或者为同一个值的数组时,可以使用稀疏数组来保存该数组。
组的处理方法是:
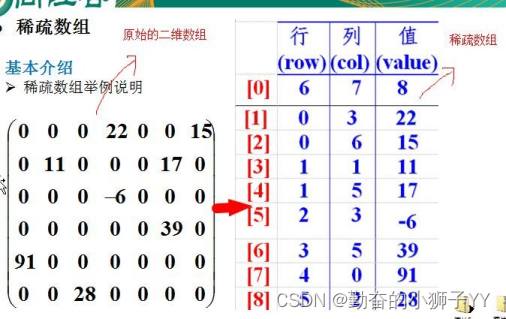
①记录数组一共有几行几列,有多少个不同的值
②把具有不同值的元素的行列及值记录在一个小规模的数组中,从而缩小程序的规模
3、稀疏数组举例说明
二、应用实例
- 使用稀疏数组,来保留类似前面的二维数组(棋盘、地图等等)
- 把稀疏数组存盘,并且可以从新恢复原来的二维数组数
- 整体思路分析

三、代码实现
package com.atguigu.sparsearray;public class SparseArray {public static void main(String[] args) {// 创建一个原始的二维数组 11 * 11// 0: 表示没有棋子, 1 表示 黑子 2 表蓝子int chessArr1[][] = new int[11][11];chessArr1[1][2] = 1;chessArr1[2][3] = 2;chessArr1[4][5] = 2;// 输出原始的二维数组System.out.println("原始的二维数组~~");for (int[] row : chessArr1) {for (int data : row) {System.out.printf("%d\t", data);}System.out.println();}// 将二维数组 转 稀疏数组的思// 1. 先遍历二维数组 得到非0数据的个数int sum = 0;for (int i = 0; i < 11; i++) {for (int j = 0; j < 11; j++) {if (chessArr1[i][j] != 0) {sum++;}}}// 2. 创建对应的稀疏数组int sparseArr[][] = new int[sum + 1][3];// 给稀疏数组赋值sparseArr[0][0] = 11;sparseArr[0][1] = 11;sparseArr[0][2] = sum;// 遍历二维数组,将非0的值存放到 sparseArr中int count = 0; //count 用于记录是第几个非0数据for (int i = 0; i < 11; i++) {for (int j = 0; j < 11; j++) {if (chessArr1[i][j] != 0) {count++;sparseArr[count][0] = i;sparseArr[count][1] = j;sparseArr[count][2] = chessArr1[i][j];}}}// 输出稀疏数组的形式System.out.println();System.out.println("得到稀疏数组为~~~~");for (int i = 0; i < sparseArr.length; i++) {System.out.printf("%d\t%d\t%d\t\n", sparseArr[i][0], sparseArr[i][1], sparseArr[i][2]);}System.out.println();//将稀疏数组 --》 恢复成 原始的二维数组/** 1. 先读取稀疏数组的第一行,根据第一行的数据,创建原始的二维数组,比如上面的 chessArr2 = int [11][11]2. 在读取稀疏数组后几行的数据,并赋给 原始的二维数组 即可.*///1. 先读取稀疏数组的第一行,根据第一行的数据,创建原始的二维数组int chessArr2[][] = new int[sparseArr[0][0]][sparseArr[0][1]];//2. 在读取稀疏数组后几行的数据(从第二行开始),并赋给 原始的二维数组 即可for(int i = 1; i < sparseArr.length; i++) {chessArr2[sparseArr[i][0]][sparseArr[i][1]] = sparseArr[i][2];}// 输出恢复后的二维数组System.out.println();System.out.println("恢复后的二维数组");for (int[] row : chessArr2) {for (int data : row) {System.out.printf("%d\t", data);}System.out.println();}}}
喜欢的话点个关注吧!

相关文章:

数据结构--稀疏矩阵及Java实现
一、稀疏 sparsearray 数组 1、先看一个实际的需求 编写的五子棋程序中,有存盘退出和续上盘的功能。 分析问题: 因为该二维数组的很多值是默认值 0, 因此记录了很多没有意义的数据.->稀疏数组。 2、稀疏数组基本介绍 当一个数组中大部分元素为0…...
关于GPU使用过程中的若干问题
1.CUDA异常 问题描述:运行torch.cuda.is_available() 报错:cuda unknown error - this may be due to an incorrectly set up environment解决方案:重启 2.nvidia驱动版本不匹配 问题描述:运行nvidis-smi 报错:Fa…...
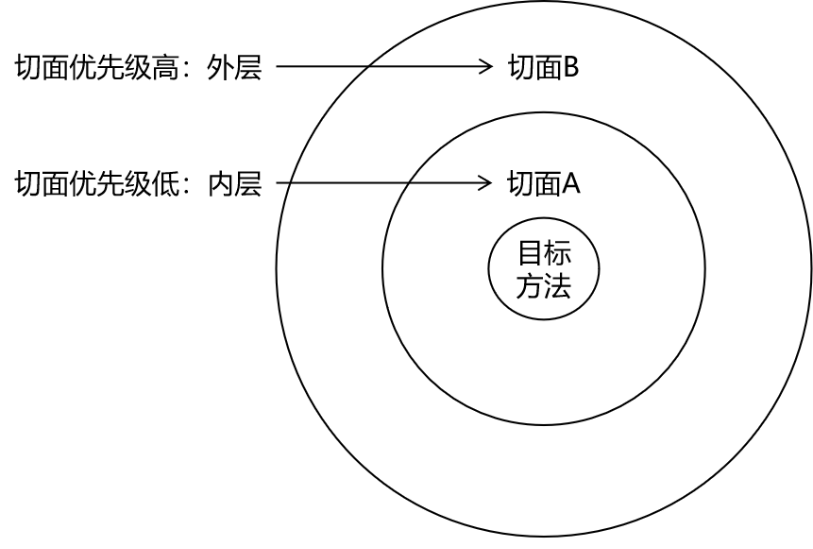
spring之面向切面:AOP(2)
学习的最大理由是想摆脱平庸,早一天就多一份人生的精彩;迟一天就多一天平庸的困扰。各位小伙伴,如果您: 想系统/深入学习某技术知识点… 一个人摸索学习很难坚持,想组团高效学习… 想写博客但无从下手,急需…...

【开题报告】基于uniapp的家庭记账小程序的设计与实现
1.研究背景 随着社会经济的发展和人们生活水平的提高,家庭财务管理变得越来越重要。家庭记账是一种重要的财务管理方式,通过记录和分析家庭的收入和支出情况,可以帮助家庭成员更好地理解和掌握自己的财务状况,合理规划和管理家庭…...

HTML5面试题
HTML5面试题 什么是HTML5?它与HTML4有何不同之处? HTML5是HTML的第五个主要版本,它引入了许多新的语义化元素、API和功能,以改进网页的结构、样式、交互和多媒体体验。 HTML5与HTML4的不同之处包括: 引入了一系列新的语…...

树莓派通过网线连接电脑并且设置设置链接wifi
好久没玩过树莓派了,系统进不去了,需要记录一下,之前总觉得自己会了,但是还是需要不断的翻阅资料。 树莓派 配置SD卡开启ssh - 哔哩哔哩 树莓派通过网线连接ssh 直接在sd卡建立一个ssh的文件,不要带任何后戳 ip查…...

C#拼接JSON
一、业务背景 最近项目需要与U8c对接,实现增删改查,借此机会,梳理一下C#解析Json字符串的问题。 这篇文章,先以新增接口为例。 二、新增接口 查看需要传入的json格式。 拼接json,无非就是{}和[]的来回嵌套。 首先&am…...

评价机器学习模型的指标
为了衡量一个机器学习模型的好坏,需要给定一个测试集,用模型对测试集中的每一个样本进行预测,并根据预测结果计算评价分数。 对于分类问题,常见的评价标准有准确率、精确率、召回率和F值等。给定测试集 𝒯 {(…...
C# WPF上位机开发(日志调试)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 程序开发的过程中,调试肯定是少不了的。比如说,这个时候,我们可以设置断点、查看变量、检查函数调用堆栈等等。…...

AR室内导航如何实现?技术与原理分析
随着科技的进步,我们生活中许多方面正在被重新定义。其中之一就是导航,尤其是室内导航。增强现实(AR)技术的出现为室内导航带来了革命性的变革。本文将深入探讨AR室内导航的技术与原理,以及它如何改变我们的生活方式。…...

计算机网络:物理层(奈氏准则和香农定理,含例题)
带你速通计算机网络期末 文章目录 一、码元和带宽 1、什么是码元 2、数字通信系统数据传输速率的两种表示方法 2.1、码元传输速率 2.2、信息传输速率 3、例题 3.1、例题1 3.2、例题2 4、带宽 二、奈氏准则(奈奎斯特定理) 1、奈氏准则简介 2、…...

天津仁爱学院专升本化学工程与工艺专业 《无机化学》考试大纲
天津仁爱学院化学工程与工艺专业高职升本入学考试《无机化学》课程考试大纲 一.参考教材 杨宏孝《无机化学简明教程》以及《无机化学简明教程学习指南》,高等教育出版社,2011年版。 二.考试基本要求 本考试要求将《无机化学》…...
GO 的 socks5代理 编写
这里学习一下 socks5 代理的编写 网上有很多 学习一下 go 语言实战入门案例之实现Socks5 - 知乎 滑动验证页面 socks5协议原理学习-腾讯云开发者社区-腾讯云 (tencent.com) 首先我们要了解一下socks5的代理方式 socks5 是基于 认证建立连接转发数据 所形成的代理 我们只…...

MYSQL-简单的联表查询示例
假设我们有两个表,一个是users表,包含用户的ID和姓名;另一个是orders表,包含订单的ID、用户ID和订单金额。我们想要关联这两个表,查询出每个用户的订单总金额。 首先,我们可以使用以下SQL查询获取每个用户…...

Python基于joblib的并行计算进程线程multiprocessing多核并行计算
文章目录 Python基于joblib的并行计算适用场景使用示例总结爬虫&joblib使用`joblib`的场景注意事项使用实例结论joblib介绍简单示例多参数并行并行时CPU是怎么分配的何时选用并行进程&线程进程和线程之间的关系...

左右列的单元格合并
EasyExcel导出合并单元格,左右列的单元格合并 1、导出的实体类,也就是表头 Data public class CityCapacityPo {ExcelProperty(value "时间",index 0)private String time;ExcelProperty(value "出口",index 1)private String …...
机器学习 | 决策树 Decision Tree
—— 分而治之,逐个击破 把特征空间划分区域 每个区域拟合简单模型 分级分类决策 1、核心思想和原理 举例: 特征选择、节点分类、阈值确定 2、信息嫡 熵本身代表不确定性,是不确定性的一种度量。 熵越大,不确定性越高,…...
【系统移植】【华清远见西安中心】)
面试题总结(十四)【系统移植】【华清远见西安中心】
你用过哪些Bootloader?有什么区别? 作为一个AI助手,我没有直接使用过Bootloader。但我可以为您提供一些关于常见Bootloader的信息和他们之间的区别。 1. GRUB (GRand Unified Bootloader):GRUB是一个功能强大且广泛使用的Bootload…...

【Spark精讲】Spark RDD弹性体现在哪些方面?
什么是“弹性”? 一般对于分布式系统,“弹性”指的是可以根据计算规模进行动态伸缩的特性。当计算量增长时,可以动态增加资源来满足计算需求,而当计算量减少时,又可以降低资源配置来节约成本。 参考:什么是…...

【从客户端理解Kafka的使用方式】
文章目录 一、从基础的客户端说起1、消息发送者主流程2、消息消费者主流程 二、从客户端属性来梳理客户端工作机制1、消费者分组消费机制2、生产者拦截器机制3、消息序列化机制4、消息分区路由机制5、生产者消息缓存机制6、发送应答机制 三、客户端流程总结四、SpringBoot集成K…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...
