数字图像处理-空间域图像增强-爆肝18小时用通俗语言进行超详细的总结
目录
灰度变换
直方图(Histogram)
直方图均衡
直方图匹配(规定化)
空间滤波
低通滤波器
高通滤波器
本文章讲解数字图像处理空间域图像增强,大部分内容来源于课堂笔记中
灰度变换
图像增强:对图像进行处理,使其更适合于某种特定的应用,有空间域图像增强和变换域图像增强
空间域图像增强是在图像的像素级别进行操作的一种方法。它直接对图像的原始像素值进行处理,常见的空间域增强技术包括直方图均衡化、滤波(如均值滤波、中值滤波)、边缘检测、锐化等
变换域图像增强是在图像变换后进行增强操作的一种技术,它使用数学变换将图像转换到一个不同的域,然后在这个域中对图像进行操作,常见的变换域增强技术包括傅里叶变换、小波变换等,这种处理通常涉及更复杂的数学原理和计算
灰度变换是图像处理中一种常见的操作,其目的是通过对图像的灰度级进行变换,改变图像的对比度、亮度或者强调图像的某些特征。这种变换通常在图像的每个像素上进行,根据像素的原始灰度值应用一个变换函数,得到新的灰度值
通常,灰度变换的一般形式可以表示为:
其中,g(x, y)是变换后的图像灰度值,f(x, y)是原始图像的灰度值,T是变换函数

若将邻域大小限制为1*1(上图的邻域为3*3),则简化为:
r、s分别是f(x,y)、g(x,y)在任意点(x,y)的灰度级
下面介绍一些常见的灰度变换函数:
1.图像反转变换
效果:灰度图像---“黑白颠倒” 彩色图像---补色
用途:适用于增强图像中暗色区域的灰色细节部分
2.对数变换
效果:把窄范围的低灰度级映射到宽范围的灰度级,把宽范围的高灰度级映射到窄范围的高灰度级
应用:压缩图像的动态范围,显示图像的傅里叶频谱图等
3.反对数变换
效果:把宽范围的低灰度级映射到窄范围的灰度级,把窄范围的高灰度级映射到宽范围的高灰度级

4.幂次(伽马)变换
效果:
扩展暗像素值,压缩亮像素值,提升暗区分辨能力
压缩暗像素值,扩展亮像素值,提升亮区分别能力
应用:用于各种图像获取、打印和显示等设备的伽马校正
演示:
一般对于航拍图而言,由于是在空中拍,拍的照片都比较亮,导致整体画面不清晰、观感不舒服,所以可以对其使用值大于1的幂次变换进行调整
import cv2
import numpy as np# 读取图像
gray_image = cv2.imread('overlooking_img.jpg', cv2.IMREAD_GRAYSCALE)# 检查图像是否成功读取
if gray_image is None:print("Error: Could not read the image.")
else:# 伽马值gamma = 1.8# 进行伽马变换gamma_corrected = np.array(255 * (gray_image / 255) ** gamma, dtype='uint8')# 窗口大小window_size = (300, 200)# 创建原始图像窗口并设置大小cv2.namedWindow('Original Image', cv2.WINDOW_NORMAL)cv2.resizeWindow('Original Image', *window_size)cv2.imshow('Original Image', gray_image)# 创建伽马校正图像窗口并设置大小cv2.namedWindow('Gamma Corrected Image', cv2.WINDOW_NORMAL)cv2.resizeWindow('Gamma Corrected Image', *window_size)cv2.imshow('Gamma Corrected Image', gamma_corrected)cv2.waitKey(0)cv2.destroyAllWindows()

5. 分段线性变换
将灰度级划归不同范围,每个范围采用不同的线性变换
优点:变换形式可根据需要任意合成
缺点:需用户输入
主要形式:1.对比度拉伸2.灰度级分层(灰度切割)3.比特平面分层(位图切割)
直方图(Histogram)
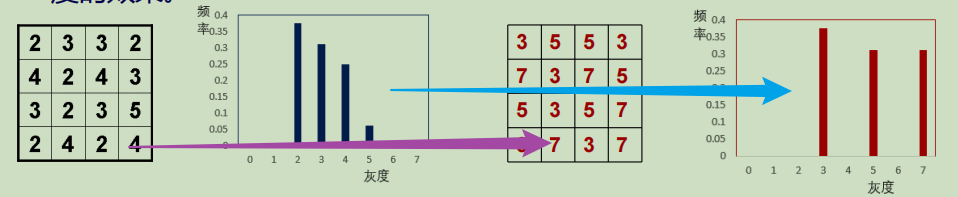
直方图表示具有不同灰度级的像素个数的条形图,把图像的灰度看作一个随机变量,则直方图是描述该随机变量的概率分布的一个近似

如上图所示,左边是普通的直方图、右边的是归一化的直方图
仅仅观察一个图像的直方图就可以看出这个图像的特点,比如说如果直方图的组成成分集中在灰度级低低的一侧,那么就是暗图像,如果直方图窄而且集中在灰度级的中间,那么就是低对比度图像等等
直方图均衡
如果想要增加像素灰度值的动态范围,从而增强图像对比度,可以使用直方图均衡,直方图均衡会使用灰度变换进行灰度修正,使得变换后的图像的直方图的灰度值分布均匀
那么,现在我们就需要找到一个灰度变换函数s=T(r)(注意:这个函数一定是个单调递增函数),将每一个r映射为s,满足:s服从均匀分布
由于r和s的定义域和值域均为[0, L - 1],则可以得到s的概率分布函数:
再由概率密度函数的基本性质可得:
所以有:
两边同时做积分,有:
对于M行N列的数字图像,灰度级出现的概率近似为:
代入,可以得到灰度变换函数的离散形式
总结:直方图均衡化处理的核心是:非线性拉伸,它可以增强图像的对比度但不改变图像内容,但在均衡过程中,原来频数较小的灰度级会被归入很少几个或一个灰度级内造成细节损失,还需要注意的是高对比度图像经直方图均衡化后,质量可能变差
直方图匹配(规定化)
修改一幅图像的直方图,使得它与另一幅图像的直方图相似,从而突出感兴趣的灰度范围,使图像质量改善就是直方图的匹配,如下图所示

那么我们如何达到上述的效果呢?很简单
假设:r、z分别表示输入图像和输出图像(或者说规定匹配的那个图像)的灰度级
第一步,我们先让r做均衡化,得到s=T(r) 有小数要四舍五入
第二步,我们让z也做均衡化,得到s'=G(z) 有小数要四舍五入
由于直方图匹配不应该改变原始图像内容,所以s=s'
那么我们推出:
第三步,找映射关系,我用下面这个图讲解该如何去找:
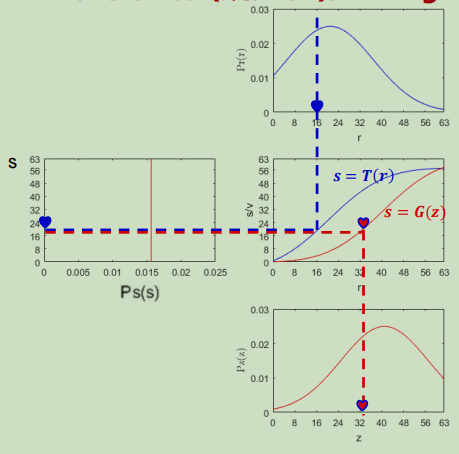
比如对于输入图像的一个灰度值r1,我们先得到s1,然后再根据s1=s2得到s2,那么这个s2的横坐标就是输出图像的灰度值z1
空间滤波
使用空间域模板进行的图像处理,称为空域滤波。模板本身被称为空域滤波器
输出图像中的每一点为输入图像中某个相关区域像素集的映射

空间滤波的基础过程:
用上述“空间域模板”在待滤波图像上移动,从蓝到红到绿,依次生成输入值14、13、14
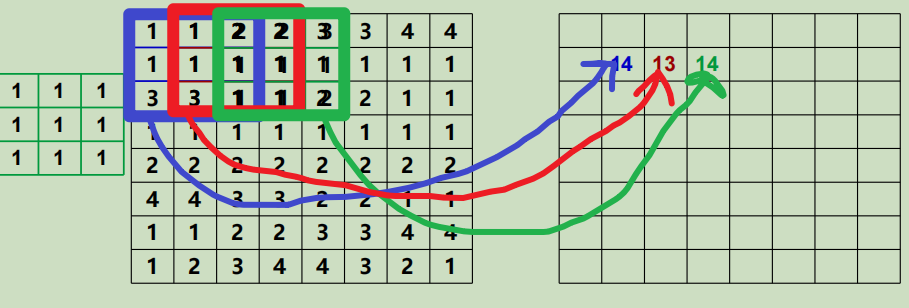
如果说图像f是M*N,滤波器w是m*n,其中m=2a+1,n=2b+1,g(x,y)是图像f经过滤波器w之后在点(x,y)的输出图像,w(s,t)是w在点(s,t)的系数,f(x,y)是原图像在(x,y)上的像素值则易得:
上式实际上是一个相关操作,还有一个操作叫做卷积,和相关非常相似,但略有不同

下面通过一个例子,直观展示两者的区别:

那么,卷积和相关相比,其优势在哪里?卷积的操作符合交换律、结合律、分配律,而相关仅仅符合分配律
低通滤波器
低通滤波器又称平滑滤波器,它可以去除图像中一些不重要的细节,比如噪声,还可以平滑图像
低通滤波器分为线性滤波器和非线性滤波器,下面细说
线性滤波器主要指均值滤波器,其一般形式如下,分为盒装滤波和加权均值滤波
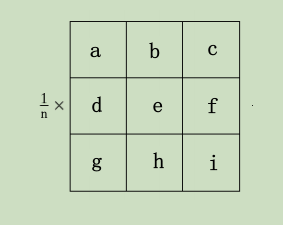
其中n=a+b+c+...+h+i
如果为盒装滤波,则a=b=c=...=h=i
如果为加权均值滤波,则a~i至少有两个值不同
非线性滤波器又称统计排序滤波器,一般分为三种:中值滤波器、最大值滤波器、最小值滤波器,这三种滤波器非常好理解,以最大值滤波器为例,输出像素就是原像素滤波范围内所有像素的最大像素值
中值滤波器可以消除孤立的亮点或暗点、有效去除椒盐噪声,同时较均值滤波器而言,更好地保留边的锐度和图像的细节

高通滤波器
高通滤波器又称锐化滤波器,它可以突出图像的细节,在超声探测成像中,可以通过锐化改善分别率低、边缘模糊等问题,同时也可以恢复过度钝化、曝光不足的图像
先简单介绍一下图像中的高频信息和低频信息,低频是指灰度变化比较小的像素区域(图像内容),高频是指灰度变化比较大的像素区域(变化或者内部纹理),而高通滤波器就是要削弱低频信息,突出高频信息,这与上述低通滤波器恰恰相反
高通滤波器当中常见的两种形式是一阶微分和二阶微分
那么,先介绍一下这两种微分的数学形式
一阶微分
二阶微分
使用二阶微分锐化图像一般用拉普拉斯算子,其定义式如下:
其中第二个等号后面是代入上述二阶微分算式后求得的偏导结果
根据拉普拉斯算子的定义,容易得到拉普拉斯算子的标准滤波模板

如果对上述的模板进行扩展,使得其能够处理对角线的四个像素,可以得到如下模板:

最后是上面两种模板的另一种形式
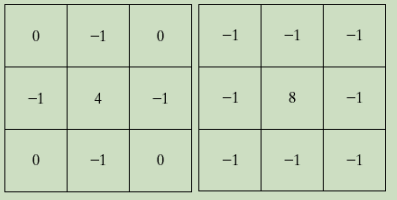
下面是使用上述两种模板进行锐化的实例,可以发现:经有对角分量的掩膜处理后的图像,比基本掩膜处理后的图像更加锐化

使用一阶微分锐化图像一般用梯度,其定义式如下:

用上述的式子很难形成滤波的模板,所以我们采取的方式是用绝对值替换
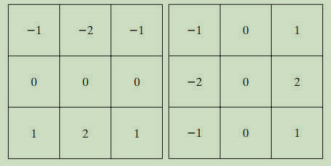
形成了下面常用的三种算子
1.Roberts交叉梯度算子

2.Prewitt梯度算子
3.Sobel梯度算子
相关文章:

数字图像处理-空间域图像增强-爆肝18小时用通俗语言进行超详细的总结
目录 灰度变换 直方图(Histogram) 直方图均衡 直方图匹配(规定化) 空间滤波 低通滤波器 高通滤波器 本文章讲解数字图像处理空间域图像增强,大部分内容来源于课堂笔记中 灰度变换 图像增强&…...

【Java】【SQL】DATE_FORMAT函数详解
在实际应用开发中,使用sql语句也属于开发者的一部分,这次来说说DATE_FORMAT函数。 引言:实际上在使用Java开发过程中,有很多业务场景下,都有时间类型的参数参与。前后端进行交互的时候,针对时间类型的格式…...
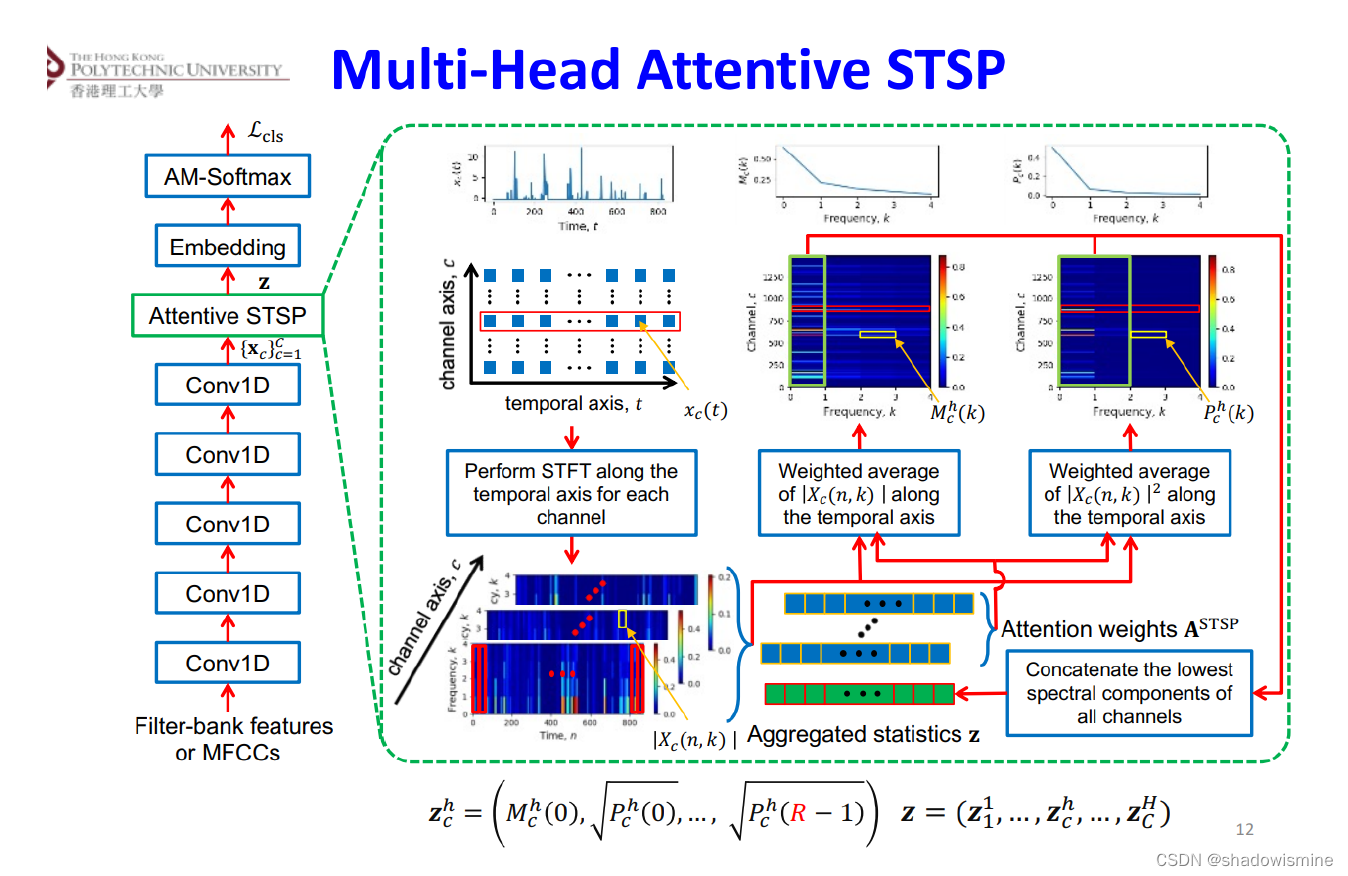
Pooling方法总结(语音识别)
Pooling layer将变长的frame-level features转换为一个定长的向量。 1. Statistics Pooling 链接:http://danielpovey.com/files/2017_interspeech_embeddings.pdf The default pooling method for x-vector is statistics pooling. The statistics pooling laye…...
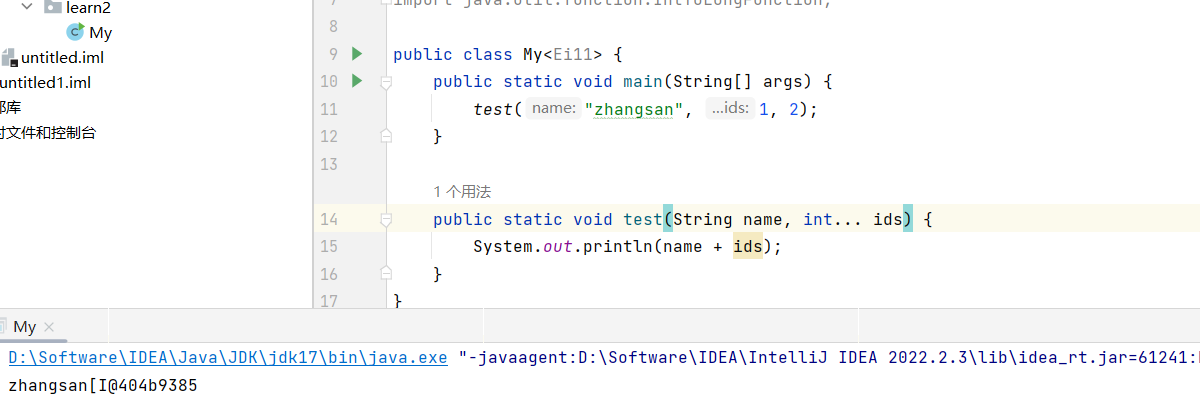
Java可变参数(学习推荐版,通俗易懂)
定义 可变参数本质还是一个数组 示例代码 注意事项 1.形参列表中,可变参数只能有一个 2.可变参数必须放在形参列表的最后面 注意是最后面。 name也可以为int类型...
异步编程Promise
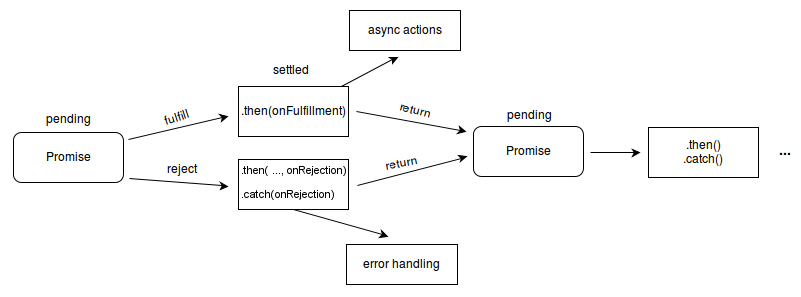
文章目录 前言一、关于 Promise 的理解与使用1.相关知识补充区别实例对象和函数对象同步回调异步回调Js中的错误(error)和错误处理 2.promise是什么 二、Promise 原理三、Promise 封装 Ajax四、async 与 await总结 前言 在项目中,promise的使…...

Centos上的默认文本编辑器vi的操作方法积累
打开一个文本后,常见的操作方法积累如下: 001-进入或退出插入模式的方法 按下 i 进入插入模式。 按下 Esc 退出插入模式。 002-进入命令模式的方法: 按下 Esc 退出插入模式,然后输入冒号:进入命令模式。 003-退出vi编辑器的方…...

海康rtsp拉流,rtmp推流,nginx部署转flv集成
海康rtsp拉流,rtmp推流,nginx部署转flv集成 项目实际使用并测试经正式使用无问题,有问题欢迎评论留言 核心后台java代码: try {// FFmpeg命令String command "ffmpeg -re -i my_video.mp4 -c copy -f flv rtmp://localho…...

【Python百宝箱】时序之美:Python 时间序列探秘与创新
时光漫游:Python 时间序列分析全指南 前言 在数字化时代,时间序列数据扮演着关键的角色,从金融到气象再到生产制造。本文将引导你穿越Python丰富的时间序列分析工具,探索从基础统计到机器学习和深度学习的各个层面。无论你是初学…...
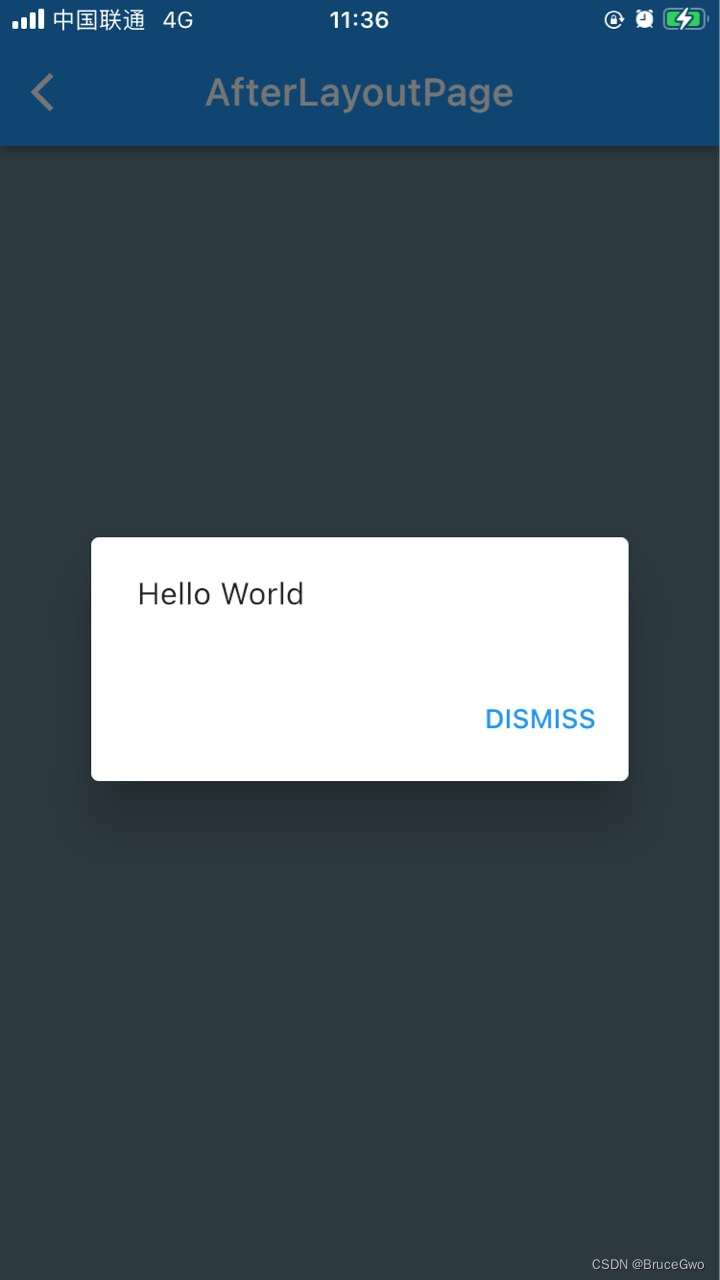
flutter开发实战-第一帧布局完成回调实现
flutter开发实战-第一帧布局完成回调实现 在开发中,我们有时候需要在第一帧布局完成后调用一些相关的方法。这里记录一下是实现过程。 Flutter中有多种不同的Binding,每种Binding都负责不同的功能。下面是Flutter中常见的Binding: 这里简单…...
Windows11编译VTM源码生成Visual Studio 工程
VTM介绍 VTM作为H266/VVC标准的官方参考软件,一直用作H266/VVC标准的研究和迭代。关于H2666/VVC标准的介绍、代码、提案、文档等,可以参考H266/VVC编码标准介绍。 官方代码地址: https://vcgit.hhi.fraunhofer.de/jvet/VVCSoftware_VTM&…...
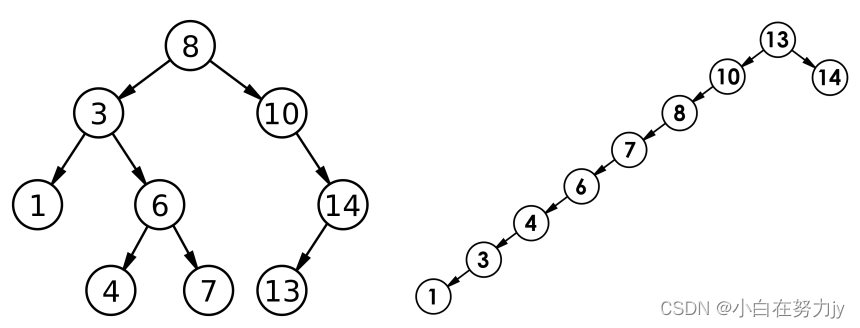
[数据结构进阶 C++] 二叉搜索树(BinarySearchTree)的模拟实现
文章目录 1、二叉搜索树1.1 二叉搜索数的概念1.2 二叉搜索树的操作1.2.1 二叉搜索树的查找1.2.2 二叉搜索树的插入1.2.3 二叉搜索树的删除 2、二叉搜索树的应用2.1 K模型2.2 KV模型 3、二叉搜索树的性能分析4、K模型与KV模型完整代码4.1 二叉搜索树的模拟实现(K模型…...
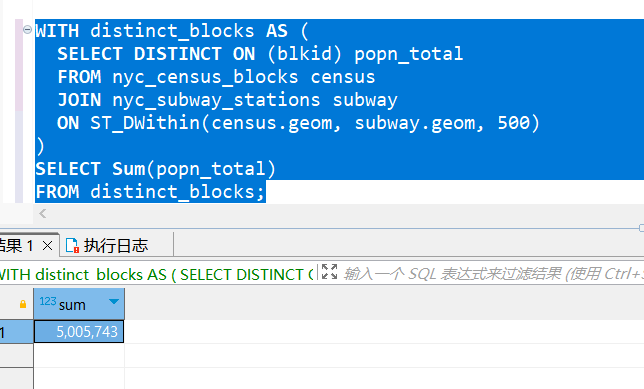
PostGIS学习教程十四:更多的空间连接
PostGIS学习教程十四:更多的空间连接 在上一节中,我们看到了ST_Centroid(geometry)和ST_Union([geometry])函数,以及一些简单的示例。在本节中,我们将用它们做一些更详细的事情。 提示:写完文章后,目录可以…...
【爬虫软件】孔夫子二手书采集
项目演示 孔网爬取图书信息 目录结构 [ |-- api-ms-win-core-synch-l1-2-0.dll, |-- api-ms-win-core-sysinfo-l1-1-0.dll, |-- api-ms-win-core-timezone-l1-1-0.dll, |-- api-ms-win-core-util-l1-1-0.dll, |-- api-ms-win-crt-conio-l1-1-0.dll, |-- api…...

P8736 [蓝桥杯 2020 国 B] 游园安排
题目描述 L \mathrm{L} L 星球游乐园非常有趣,吸引着各个星球的游客前来游玩。小蓝是 L \mathrm{L} L 星球 游乐园的管理员。 为了更好的管理游乐园,游乐园要求所有的游客提前预约,小蓝能看到系统上所有预约游客的名字。每个游客的名字由一…...
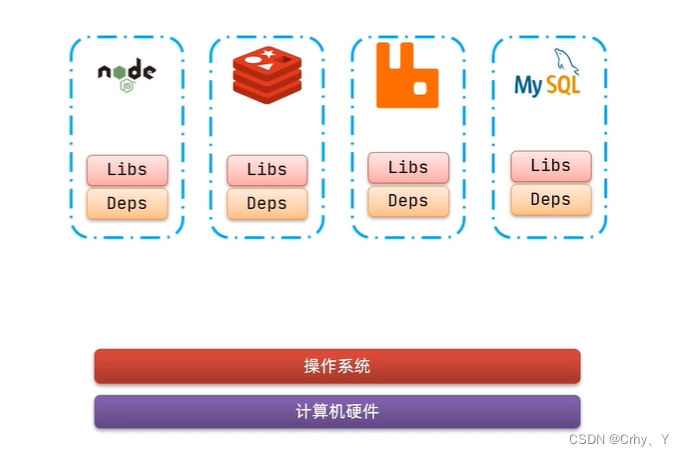
初识Docker-什么是docker
Docker是一个快速交付应用、运行应用的技术 目录 一、Docker 二、运用场景 一、什么是Docker?它的作用是什么? Docker如何解决大型项目依赖关系复杂,不同组件依赖的兼容性问题? Docker允许开发中将应用、依赖、函数库、配置一起打包&…...

maven的pom.xml设置本地仓库
配置 在Maven项目中,您可以在pom.xml文件中配置本地仓库的路径。在pom.xml文件中,您可以添加以下配置来指定本地仓库的路径: <project>...<repositories><repository><id>local-repo</id><url>file://…...

Qt获取屏幕DPI缩放比
获取屏幕缩放比 网上很多代码是用 logicalDotsPerInch 除以 96 来获取屏幕缩放比: // Windows 除以 96,macOS 除以 72 qreal factor window->screen()->logicalDotsPerInch() / 96.0; 当使能了缩放适配后,logicalDotsPerInch 值就不…...

Spring MVC控制层框架
三、Spring MVC控制层框架 目录 一、SpringMVC简介和体验 1. 介绍2. 主要作用3. 核心组件和调用流程理解4. 快速体验 二、SpringMVC接收数据 1. 访问路径设置2. 接收参数(重点) 2.1 param 和 json参数比较2.2 param参数接收2.3 路径 参数接收2.4 json参…...
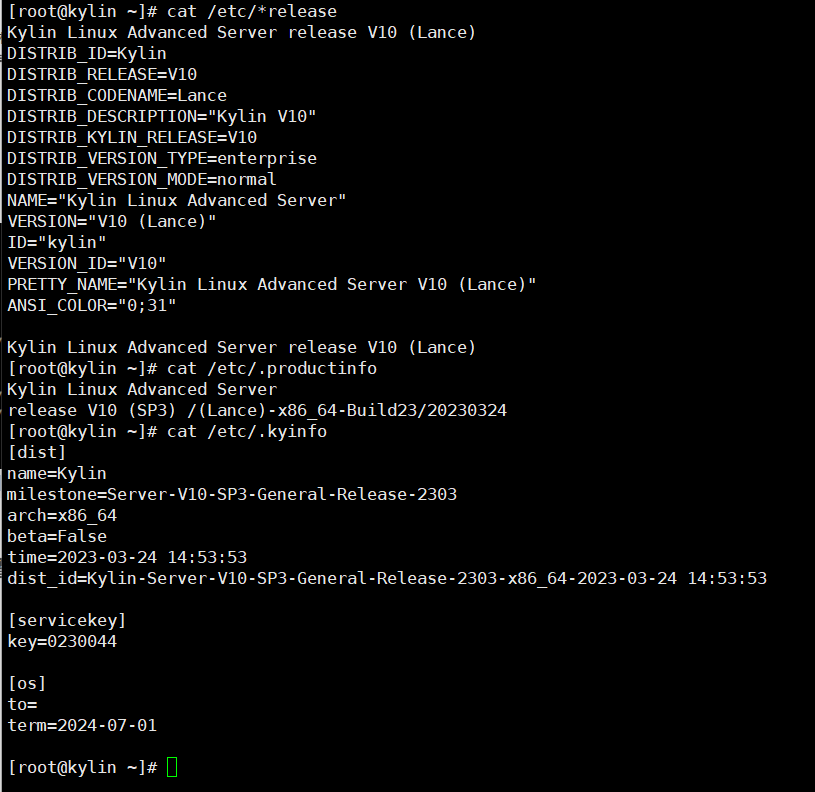
vmware安装银河麒麟V10高级服务器操作系统
vmware安装银河麒麟V10高级服务器操作系统 1、下载银河麒麟V10镜像2、VMware安装银河麒麟V10高级服务器操作系统2.1、新建虚拟机2.2、安装虚拟机 3、配置银河麒麟V10高级服务器操作系统3.1、安装vmware tools3.2、配置静态IP地址 和 dns3.3、查看磁盘分区3.4、查看系统版本 1、…...

掌握Jenknis基础概念
目录 任务(Jobs) 构建(Builds) 触发器(Triggers) 构建环境(Build Environment): 插件(Plugins): 参数化构建(Paramet…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...
